聚焦空间几何体的最值问题

■王先阳

空间几何体主要研究空间中点、线、面之间的位置关系,与空间图形有关的线段、角、面积、体积等最值问题是高考的常考点。此类问题涉及知识面广,灵活性较大,解题时需要较强的空间想象能力和思维能力。

一、线段问题

例1 如图1,在棱长为2 的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在线段D1E上,则点P到直线CC1的距离的最小值为( )。

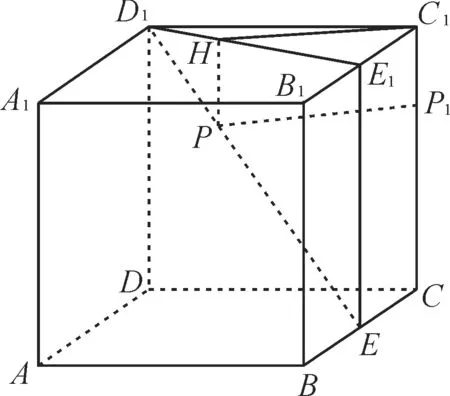
图1

二、角度问题

三、面积问题

例3 如图2,在棱长为1 的正方体ABCD-A1B1C1D1中,若G,E分别是BB1,C1D1的中点,点F是正方形ADD1A1的中心,则四边形BGEF在正方体侧面及底面共6个面内的射影图形面积的最大值是____。

图2

评注：解答本题的关键是找到四边形BGEF的四个顶点在各个侧面上的投影点的位置,再根据正方体的性质计算其射影图形面积。需要注意的是正方体有6个面,共有6种情况。

四、体积问题

例4 我国古代的数学名著《九章算术》中有这样一些数学用语,“堑堵”意指底面为直角三角形,且侧棱垂直于底面的三棱柱,而“阳马”指底面为矩形且有一侧棱垂直于底面的四棱锥。现有一如图3 所示的“堑堵”,即三棱柱ABC-A1B1C1,其中AC⊥BC,若AA1=AB=1,当“阳马”(四棱锥B-A1ACC1)体积最大时,“堑堵”(三棱柱ABC-A1B1C1)的表面积为( )。

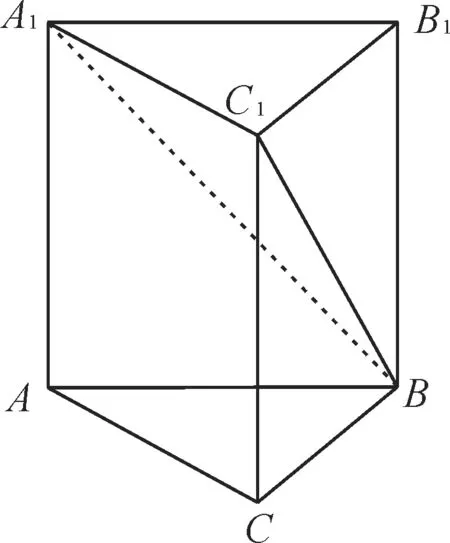
图3

已知直三棱柱ABC-A1B1C1的侧棱长为6,且底面是边长为2的正三角形,用一平面截此棱柱,与侧棱AA1,BB1,CC1分别交于三点M,N,Q,若△MNQ为直角三角形,则该直角三角形斜边长的最小值为( )。

A.2 2 B.3 C.2 3 D.4

提示：如图4 所示,不妨设点N在点B处,AM=h,CQ=m。

图4