探求线面平行中平行关系的寻找方法

■甄新锋

线面平行是指直线与平面平行,是一种常见的空间位置关系。证明直线与平面平行,关键是在所给平面内寻找一条与已知直线平行的直线。下面就线面平行中平行关系的寻找方法进行归纳,以期对同学们探索线面平行有所帮助。

一、利用三角形的中位线定理寻找线线平行

在证明线面平行时,可以构造合适的三角形,利用三角形的中位线定理和线面平行的判定定理证明线面平行。

例 1 如图 1 所示,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点。求证:AB1//平面BC1D。

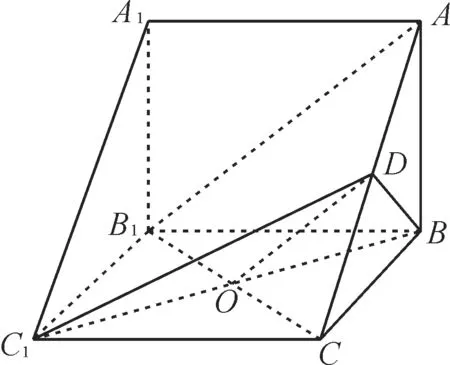
图1

证明：设B1C与BC1交于点O。

因为平面BCC1B1是平行四边形,所以O是BC1的中点。

又D是AC的中点,所以OD是△ACB1的中位线,所以OD//AB1。

因为OD⊂平面BC1D,AB1⊄平面BC1D,所以AB1//平面BC1D。

方法点拨：在构造三角形的中位线时,要注意关注中点、线段的垂直平分线、三角形的重心等信息,结合图形的特征寻找中位线。

二、利用平行四边形的性质寻找线线平行

在证明线面平行时,大胆平移,合理猜想,构造平行四边形,利用平行四边形的性质证明直线与直线平行,即得直线与平面平行。

例2 如图2,在四棱锥P-ABCD中,AD//BC,AD=2BC,M为PD的中点,证明:CM//平面PAB。

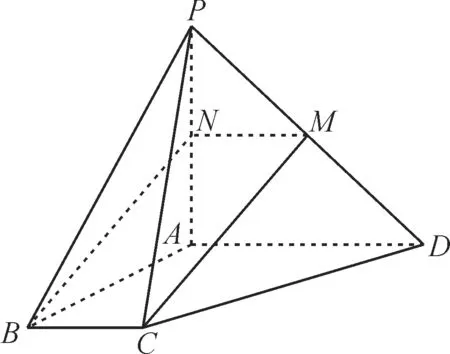
图2

因为CM⊄平面PAB,BN⊂平面PAB,所以CM//平面PAB。

方法点拨：通过直观观察,若平面内的一条直线与平面外的一条直线长度相等,一般猜想构造平行四边形,这时利用平行四边形对边平行得出线线平行,进而得到线面平行。

三、利用相似比寻找线线平行

如果一条直线截三角形的两边(或两边的延长线)所得的对应线段成比例,那么这条直线平行于三角形的第三边,这也是得到线面平行的一种有力工具。

1.4 光照。蚕豆是喜光的长日照作物，对光照的反应有一定的适应性。适宜的日照（一般为12～14小时以上），能够有效促进植株开花结实。蚕豆光合生产率有两个高峰期，一是在开花结荚期，一是在鼓粒灌浆期。

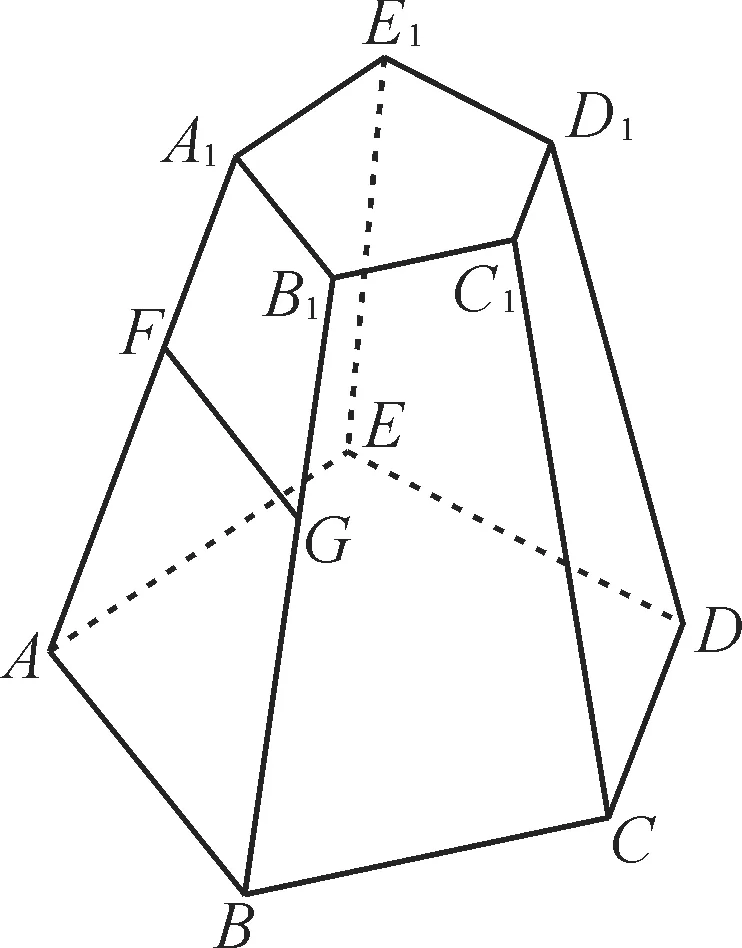
图3

方法点拨：利用比值关系,寻找线线平行,进而得到线面平行。

四、利用直线与平面平行的性质定理寻找线线平行

利用直线与平面平行的性质定理得到直线与直线平行,进而得到直线与平面平行。

例4 如图4 所示,ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH,求证:GH//平面PAD。

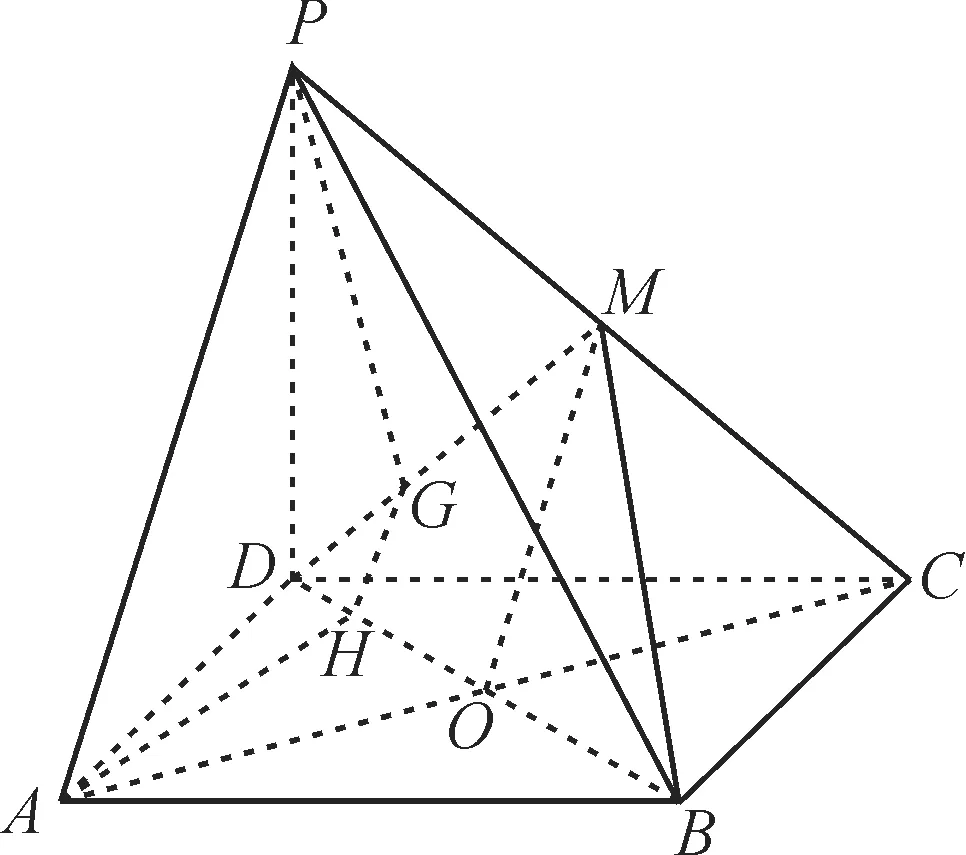
图4

证明：设AC与BD交于点O。

在△APC中,MO是△APC的中位线,所以MO//PA。因为PA⊄平面MBD,MO⊂平面MBD,所以PA//平面MBD。

因为平面GAP∩平面BDM=GH,PA⊂平面GAP,所以PA//GH。

又GH⊄平面PAD,PA⊂平面PAD,所以GH//平面PAD。

方法点拨：先证明线面平行,再利用线面平行的性质定理,得到线线平行,进而得到线面平行。

1.在三棱锥A-BCD中,E,F分别是AB和BC上的点,若AE∶EB=CF∶FB=2∶5,则直线AC与平面DEF的位置关系是( )。

A.平行

B.相交

C.直线AC在平面DEF内

D.不能确定

提示：由AE∶EB=CF∶FB=2∶5,可得EF//AC。因为EF⊂平面DEF,AC⊄平面DEF,所以AC//平面DEF。应选A。

提示：利用特殊化法求四棱锥B-APQC的体积。取三棱柱ABC-A1B1C1为直棱柱,且P,Q为侧棱中点,如图5所示。

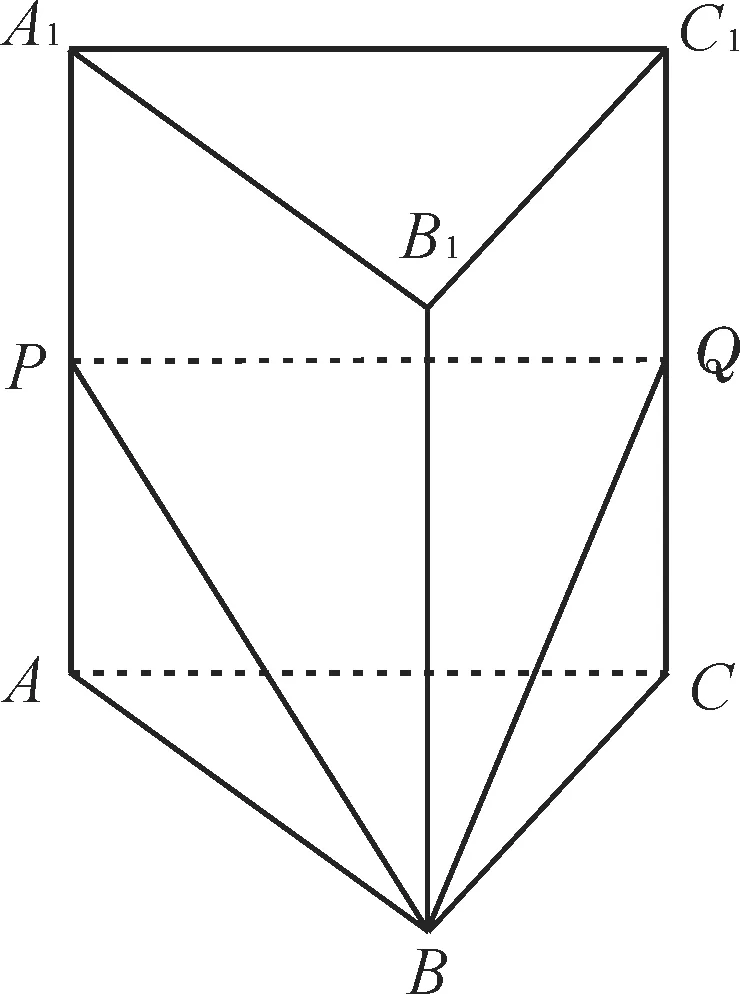
图5