自适应变阻力特征加油稳定伞设计及气动特性研究

黄 霞，吴金华，刘志涛，郭林亮

(中国空气动力研究与发展中心，四川，绵阳 621000)

软式空中加油是目前国际上主流的加油方式，其中“软管-锥套”系统是软式加油的重要部件，位于锥套前端的稳定伞是其核心组成部分，主要功能是产生阻力，从加油吊舱中拉出“软管-锥套”系统，当受油探头与锥套的加油接头对接时，增加捕捉范围，提升软管和锥套的稳定性[1-2]。

加油稳定伞有三个主要设计参数—伞撑角、伞衣面积和间隙面积，稳定伞的阻力特性与这三个参数密切相关。国内外针对稳定伞的阻力特性开展了大量的研究工作。Shigeo 等[3]建立了锥套的2D 模型，运用CFD 分析与独特的2D 风洞试验两种方法，通过改变迎角分析了稳定伞各方向的受力情况。Kapseong 等[4-5]采用了一种全因子试验方案，通过提取稳定伞三个主要参数，建立了稳定伞的参数化模型，并分别由风洞实验和数值模拟得出了稳定伞阻力系数与此三个参数的近似解析关系式，为稳定伞设计提供了参考；之后又提出通过改变稳定伞支撑角来改变气动阻力的观点，并利用MATLAB /Simulink 对大气紊流下的锥套运动进行了模拟，验证了支撑角对气动阻力的影响[6]。Andrew 等[7]研究了加油软管的气动弹性响应对稳定伞阻力特性的影响。García-Fogeda 等[2]通过在软管与稳定伞连接处安装控制面研究了软管-锥套系统的动态响应。国内石超等[8]通过CFD 方法研究了锥套支柱数对锥套稳定伞阻力系数的影响；程小芩等[9]基于CFD 研究了国外某型锥套的气动特性，通过改变锥套支撑臂数量、空速以及稳定伞面积3 个因素，构建了不同的三维子模型，利用数值计算分析了其对锥套气动特性的影响，并探究了影响规律。

目前国内外所使用的加油稳定伞主要有两类：第一类是恒定阻力特征稳定伞，加油过程中稳定伞的外形保持不变，阻力特征(即伞衣有效迎风面积)恒定，阻力值随飞机飞行速度变化而发生改变，稳定伞与加油机的相对位置也随之改变，受加油包线限制，无法同时满足高速和低速飞机加油需求，通用性较差；第二类是可变阻力特征稳定伞，其基本设计思路是通过调节伞撑角或伞衣面积改变稳定伞阻力特征面积，使得稳定伞能在不同风速下保持恒定阻力，稳定伞下沉位置相对固定，以实现同一加油机平台上同时满足多型号飞机的加油需求。

目前国外已经发展了多种可变阻力特征技术，如双层伞衣结构控制技术、活动骨架技术、更先进的自适应变阻技术等。双层伞衣结构稳定伞拥有前后两个伞衣，高速使用时为减小阻力特征使用其中一个伞衣作为迎风面，低速使用时为增大阻力特征使用两个伞衣同时作为迎风面，这种结构方式在使用时需利用其他控制机构实现伞衣的转换。活动骨架稳定伞的骨架可根据需求增大或缩小，从而改变伞衣迎风面积，在使用时也需要控制机构实现骨架伸缩。文献[10]给出了William 等设计的一种典型的活动骨架稳定伞，通过一套复杂的控制器来移动骨架。而自适应变阻稳定伞则是在结构中加入弹性元件，使得稳定伞所受风载发生变化时，弹性元件自适应控制伞衣迎风面积，而无须其他控制装置。William 等[11-12]设计了多种弹簧骨架自适应变阻稳定伞，在骨架不同位置安装弹簧来控制伞衣的移动。英国Cobham 公司则基于先进的骨架弹簧片技术研制出了多项可变阻力特征稳定伞供美国、欧洲客户使用，实现在同一加油机平台上同时满足直升机和固定翼飞机加油的需求。该技术主要是通过弹簧片受载变形来调整伞衣迎风角，从而改变伞衣迎风面积，起到稳定阻力的作用。但是可能基于保密的原因，关于国外自适应变阻稳定伞的具体设计和相关气动特性研究工作鲜有报道。

目前我国空中加油使用的稳定伞均为恒定阻力特征稳定伞，无法满足多种飞机空中加油需求。在变阻稳定伞方面，近年来也有部分学者展开了研究。陈乐乐等[13]、吴成林[14]对某型主动控制式变伞撑角稳定伞的变阻过程进行了动态特性研究，仿真分析了稳定伞变阻时软管－锥套系统的动态响应过程；周学[15]对比分析了国内外加油技术的发展趋势，初步提出了可变阻力特征技术的研究方向。但在自适应变阻力特征稳定伞的气动特性研究方面，国内仍鲜见研究。

由于自适应变阻力特征稳定伞气动特性涉及流体、柔性织物、弹性元件变形等多方面的流固耦合问题，数值计算很难准确模拟[16-17]，因此开展风洞试验研究是目前最为有效的手段。基于此，本文采用骨架弹簧片原理，设计一种全新的自适应变阻加油稳定伞，并通过风洞测力试验和变形测量技术研究不同弹簧片参数对其气动特性的影响，验证该设计方法的正确性。

1 自适应变阻力特征稳定伞设计

1.1 设计原理

本文基于骨架弹簧片原理设计自适应变阻力特征稳定伞。如图1 所示，伞衣的骨架弹簧片因受力变形改变伞衣迎风角(弹簧片与气流方向的夹角)，气流速度增大时压迫弹簧片使伞衣迎风角减小、伞衣有效迎风面积减小，当气流速度减小时释放弹簧片使伞衣迎风角增大、伞衣有效迎风面积增大，维持总阻力基本不变。

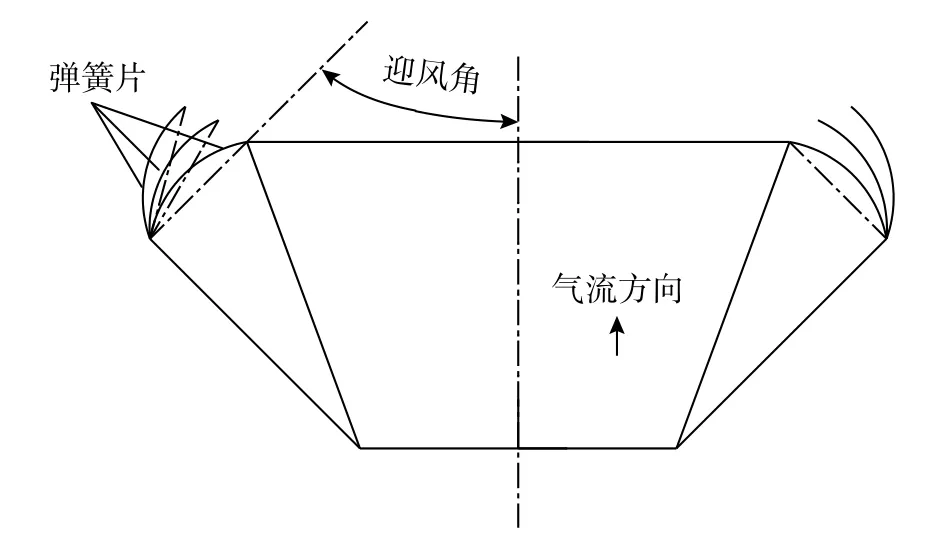
图1 骨架弹簧片原理示意图Fig. 1 Schematic diagram of skeleton spring

1.2 设计方法

本文所设计的变阻稳定伞为1∶1 比例的原型稳定伞，外形结构如图2 所示，实物如图3 所示，包括36 组支撑臂骨架、弹簧片、伞衣、固定环等部件，完全打开时最大外径尺寸960 mm，最大内径尺寸450 mm，骨架材料为铝合金。36 组支撑骨架为活动部件，通过固定环上的安装槽穿过圆环均匀分布安装，每一片支撑骨架可绕圆环自由转动，以实现稳定伞的打开与收缩；相邻两片支撑臂由钢丝绳连接，钢丝绳穿过后支撑臂上的安装孔，两端由钢质接头压紧，形成上下两组钢丝绳圈，一方面维持稳定伞打开过程中的骨架形状，另一方面限制稳定伞最大打开尺寸，以增加加油过程中稳定伞的稳定性；与传统支撑骨架相比，后支撑臂长度缩短，可有效减轻稳定伞重量；骨架弹簧片采用插槽形式安装于前支撑臂弧形槽处，使得弹簧片可以通过弧形槽调整初始迎风角度且便于更换。

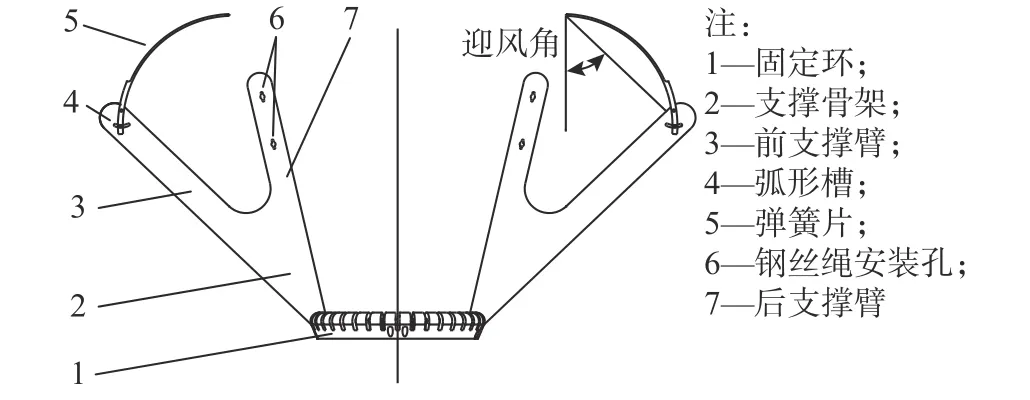
图2 自适应变阻稳定伞结构示意图Fig. 2 Structural diagram of adaptive variable drag drogue

图3 自适应变阻稳定伞实物照片Fig. 3 Picture of adaptive variable drag drogue

目前我国使用的稳定伞为传统恒定阻力特征稳定伞，伞衣直接连接在前支撑臂和后支撑臂末端，环状伞衣处于无约束状态；而本文设计的稳定伞增加了弹簧片元件，伞衣套在弹簧片外面，起到维形的作用。伞衣为双层缝制的篷布，具有良好的柔韧性和强度，厚度约1.2 mm，呈圆环状，伞衣上均匀缝制36 个宽度约为20 mm 的布套，使其能将18 mm 宽的弹簧片套入其中但又不松动，伞衣将36 片弹簧片连接在一起，形成环状伞衣成为产生阻力的主要部件，伞衣受风载后，弹簧片发生变形，从而改变伞衣的迎风角度和有效迎风面积，起到变阻力特征面积的作用。

1.3 设计难点

弹簧片是本文所设计稳定伞的关键部件(设计细节如图4 所示)，其材料及结构外形参数如何选取是最大的设计难点。

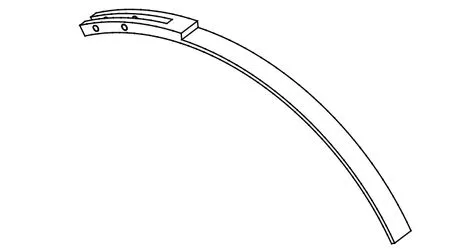
图4 弹簧片细节设计图Fig. 4 Detailed design figure of spring leaf

弹簧片变形与抗弯刚度相关，抗弯刚度越小变形越大；抗弯刚度与弹簧片材料的弹性模量以及弹簧片横截面积相关，弹性模量和横截面积越小，抗弯刚度越小。因此弹簧片设计涉及材料属性(弹性模量、塑性屈服强度)、长度、宽度、厚度、弯曲形状等多个参数。

由于稳定伞自适应变阻过程涉及流体、柔性织物、弹性元件变形等多方面的流固耦合问题，理论分析和数值计算都很难准确模拟该过程，亦无法直接给出有效的弹簧片材料结构参数。因此本文拟采用风洞试验方法来探索弹簧片的设计参数。

本文仅研究弹簧片材料弹性模量和弹簧片厚度两个关键参数对自适应变阻稳定伞气动特性的影响。基于工程经验，初步设计两种材料、三种厚度共四种弹簧片模型开展风洞试验，分别为厚度8.0 mm、1.5 mm、1.0 mm 的钢弹簧片(45#钢)和厚度1.0 mm 的钛合金弹簧片(TC4 钛合金)。45#钢和TC4 钛合金的弹性模量分别为209 GPa 和110 GPa，则四套弹簧片的抗弯刚度大小关系为：8.0 mm 钢＞1.5 mm 钢＞1.0 mm 钢＞1.0 mm 钛合金。

2 风洞试验方法

本文通过开展稳定伞测力试验和变形测量来研究自适应变阻力特征稳定伞的气动特性，验证变阻设计方法的正确性。

试验在中国空气动力研究与发展中心FL-14风洞(φ3.2 m 风洞)开口试验段进行。为减小支撑装置对稳定伞气动特性的干扰影响，采用尾撑支撑方式，模型安装如图5 所示。

图5 模型安装图Fig. 5 Model installation diagram

图6 给出了试验装置的结构示意图，安装座和整流罩模拟了加油接头的外形，天平浮动端与安装座连接，天平固定端与支杆连接。试验时天平轴线、支杆轴线与风洞来流方向平行，使加油稳定伞处于零迎角、零侧滑角状态。

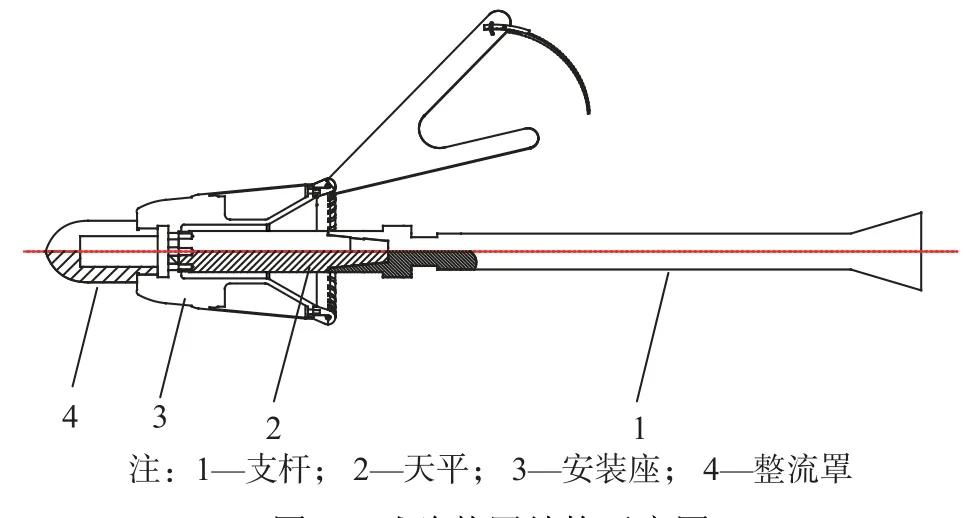
图6 试验装置结构示意图Fig. 6 Structural diagram of test device

由于稳定伞既有柔性织物又涉及弹簧片变形，与传统刚性模型测力试验相比，模型的稳定性明显降低，因此对测力试验结果分别采用静态和动态数据分析两种方式。气动载荷由TS0802A六分量杆式天平测量，通过风洞PXI 数采系统采集，采样时间为6 s、采样频率100 Hz，静态结果为6 s 内采样结果的平均值，动态结果为6 s 内采样值的实时序列。

弹簧片在不同风速下的变形由OptiTrack 系统测量。OptiTrack 为光学运动捕获系统，属于被动式红外光学定位技术，原理是利用多个红外摄像头发出波长850 nm 的红外线光照射到标记点上，由于标记点上的反光材料具有增强红外光线的反射能力，从而达到图像中标记点与周围环境明显区分的目的，获得标记点的位移信息。对同一标记点，只要它同时为两个相机所见，即可根据摄影测量原理确定这一时刻该点在空间中的三维位置坐标。为确保试验中能有效获得标记点的空间位置信息，在试验段上方安装5 台红外相机，安装位置如图7 所示；在稳定伞上方弹簧片对应的伞衣上粘贴8 个～9 个标记点，标记点黏贴位置如图8所示。试验前标定OptiTrack 系统坐标系，坐标系定义如图7 所示，原点位于锥套前缘端点，z轴平行于来流指向前，y轴垂直于z轴指向正上方，x轴满足右手定则。OptiTrack 系统红外相机拍摄帧率设置为30 fps，拍摄时间5 s。

图7 OptiTrack 系统红外相机安装图Fig. 7 OptiTrack infrared cameras installation diagram

图8 标记点粘贴位置Fig. 8 Paste location of marks

试验按稳速压方式运行，速压控制精度为0.3%，试验风速范围30 m/s～80 m/s。待速压稳定后，同步采集对应风速下的气动载荷及标记点三维坐标信息。由于弹簧片受载会发生变形，且风速越高变形越大，甚至可能发生断裂，在洞内安装防护网进行保护。

3 试验结果及分析

本文仅对初始迎风角度为38°的稳定伞气动特性结果进行分析，关于不同初始迎风角度对稳定伞气动特性的影响，鉴于文章篇幅限制将另文讨论。

3.1 变形结果分析

图9 给出了四种弹簧片在不同风速下的变形结果，图中曲线是各标记点在OptiTrack 系统坐标系oyz平面内的投影点的连线，体现了不同锥套弹簧片变形后的形状。从图中可以看出，对于8.0 mm钢弹簧片稳定伞，当风速为30 m/s～40 m/s 时，骨架处于打开过程阶段，标记点位置坐标随风速增加逐渐上移；当风速大于40 m/s 以后，骨架完全打开，随风速增加，各标记点位置坐标基本不再变化，弹簧片形状曲线重合，表明8.0 mm 钢弹簧片的抗弯刚度很大，在试验风速范围内未发生变形，始终处于刚性状态；其他三种弹簧片均发生变形，且风速越大变形越大；1.0 mm 钢弹簧片稳定伞骨架最易打开，风速30 m/s 时已基本完全打开。

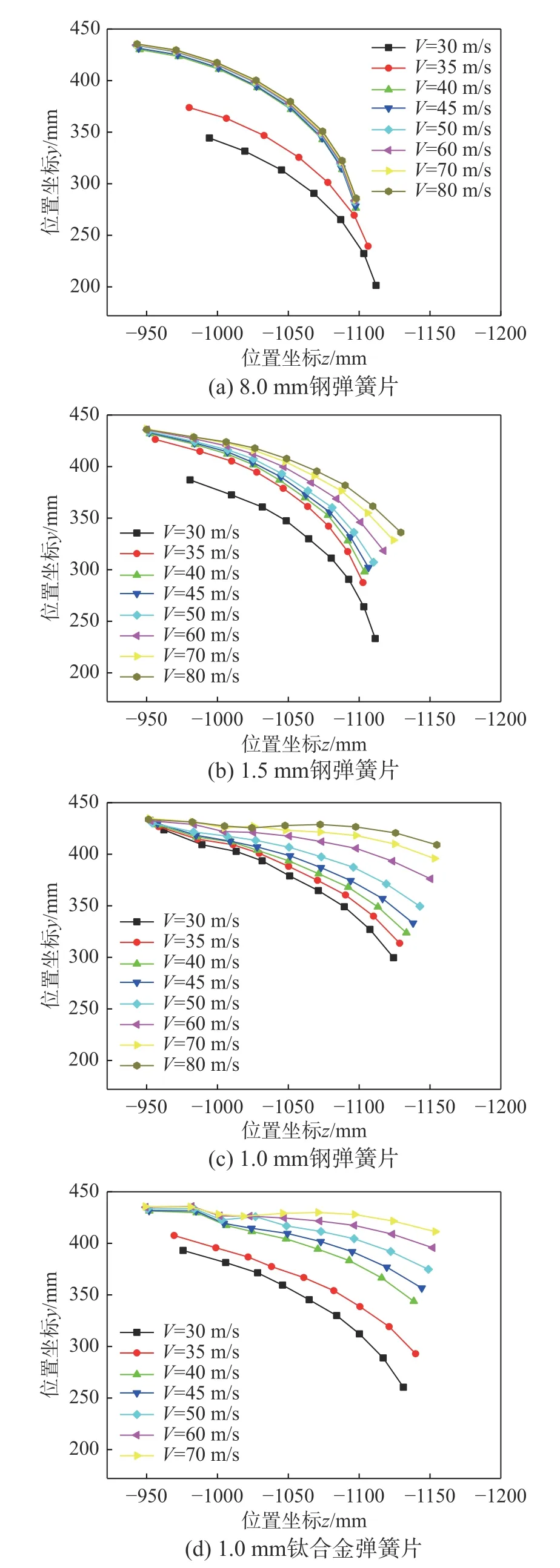
图9 不同风速下弹簧片的变形结果Fig. 9 Deformation results of spring under different wind speeds

图10 给出了风速分别为40 m/s 和70 m/s 时，不同弹簧片的变形对比结果。结果表明，弹簧片抗弯刚度越小，变形越大，变形大小关系为1.0 mm钛合金＞1.0 mm 钢＞1.5 mm 钢，风速70 m/s 时，1.0 mm 钛合金弹簧片几乎与来流方向平行。

图10 相同风速下，不同弹簧片的变形对比结果Fig. 10 Deformation comparison of different springs at thesame wind speed

3.2 测力试验静态结果分析

加油稳定伞环形伞衣是为锥套提阻力的主要部件，其核心指标为阻力特征值CA(也称为阻力特征面积)，表征伞衣的有效迎风面积，计算公式为：CA=FD/q。其中：FD为测得的阻力值；q为速压。

图11、图12 分别给出了不同弹簧片稳定伞的阻力和阻力特征对比曲线。结果表明，当骨架弹簧片为8.0 mm 钢时，弹簧片保持刚性状态，随风速增大，有效迎风面积基本不发生变化，稳定在0.43 m2左右，阻力值则迅速增大，即8.0 mm 钢弹簧片稳定伞表现出恒定几何特征的性质，其气动特性规律与传统稳定伞相关数值计算和风洞试验规律完全一致[5,9]。弹簧片为1.5 mm 钢、1.0 mm钢和1.0 mm 钛合金时，由于受风载后弹簧片发生了变形，伞衣的迎风角度随之改变，因此稳定伞有效迎风面积随风速增加而逐渐减小，阻力值增幅减小，表现出变阻力特征的性质；且抗弯刚度越小，变形越大，有效迎风面积减小越显著；特别是1.0 mm 钢和1.0 mm 钛合金弹簧片稳定伞，阻力的变化梯度较小，充分体现了自适应变阻力特征稳定伞随风速变化阻力值相对稳定的特点，验证了本文自适应变阻力特征稳定伞设计方法的正确性。此外，当弹簧片变形到一定程度，即实际迎风角减至接近0°后，随风速增加，弹簧片将不会继续变形，会维持现有形状，有效迎风面积趋于稳定，阻力值将持续快速增加，稳定伞自适应变阻特性失效；由于1.0 mm 钛合金弹簧片更易变形，其失效风速(70 m/s 左右)比1.0 mm 钢弹簧片稳定伞(80 m/s 左右)低，有效自适应变阻风速区间更窄。综上1.0 mm 钢弹簧片稳定伞的自适应特性更优。

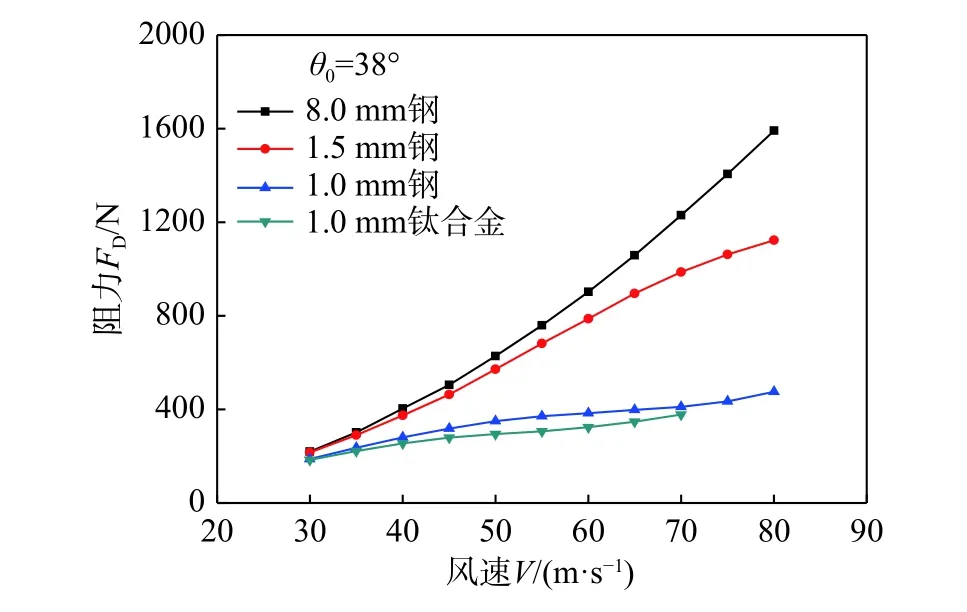
图11 不同弹簧片稳定伞的阻力曲线Fig. 11 Drag curves of drogues with different springs

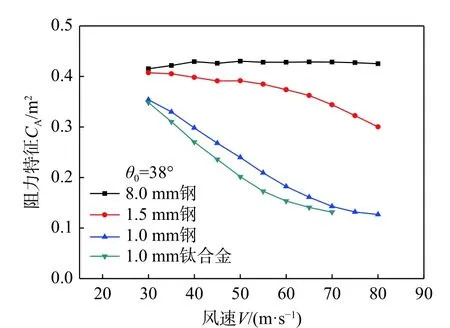
图12 不同弹簧片稳定伞的阻力特征曲线Fig. 12 Drag characteristic curves of drogues with different springs

3.3 测力试验动态结果分析

对于稳定伞测力试验，由于伞衣是柔性布，试验时会出现呼吸作用，导致数据稳定性降低。因此对四种弹簧片稳定伞的动态测量数据结果展开了研究，并与某型传统恒定阻力特征稳定伞的动态测量结果进行了对比。图13 给出了风速70 m/s时，不同稳定伞阻力特征动态测量结果的对比曲线；图14 给出了不同风速下，不同稳定伞阻力特征动态测量结果的标准差对比曲线。

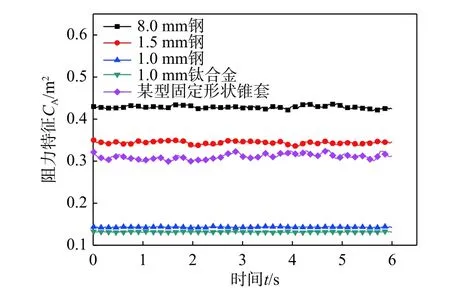
图13 风速70 m/s，不同稳定伞阻力特征的动态测量结果对比曲线Fig. 13 V=70 m/s, comparison curves of dynamic results of drag characteristics for different drogues

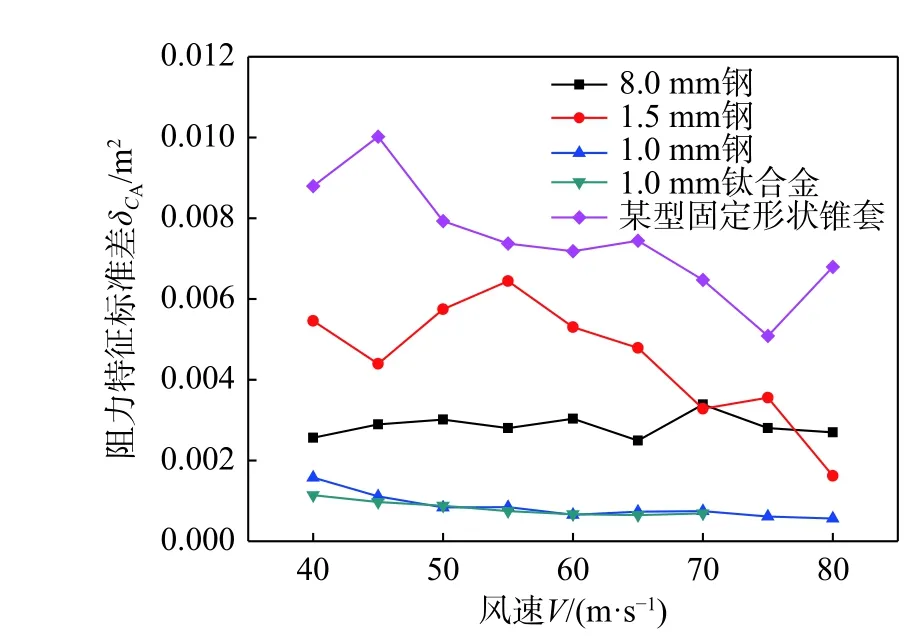
图14 不同风速下，不同稳定伞阻力特征动态测量结果的标准差对比曲线Fig. 14 Under different wind speeds, standard deviation comparison curves of dynamic results of drag characteristics for different drogues

结果表明，本文设计的稳定伞结构由于增加了弹簧片元件，对伞衣有维形作用，不再如传统稳定伞一般整个环状伞衣处于自由无约束状态，因此伞衣的动态稳定性明显优于传统稳定伞。尤其是骨架弹簧片为1.0 mm 钢和1.0 mm 钛合金时，稳定伞的阻力特征动态测量数据波动及离散标准差值显著降低，表明这两种稳定伞稳定特性更好，这也验证了其自适应特性对于提升阻力稳定性十分有利。

4 数据结果的拓展与应用

由于风洞条件限制，本文仅进行了低速试验研究，在试验风速范围内得到了1.0 mm 钢弹簧片稳定伞的自适应特性更优的结论，如图11 所示，其能在50 m/s～75 m/s 风速范围内自适应变形调节阻力特征面积，保持稳定伞的阻力值相对稳定。但是该阻力值偏小，所对应的飞行速度偏低，并不适用于在真实加油飞行中直接使用。

以下将对本文所获得的试验结果进行拓展应用，提炼出工程估算模型，为下一步开展工程适用的自适应变阻稳定伞设计提供有效的弹簧片输入参数。

4.1 工程估算模型

式(4)即为工程估算模型，给出了两种弹簧片变形规律一致时，对应的风速关系。

企业的管理者要想更好地了解公司的实际情况，就要注意采纳下层员工的意见。在新的时代背景下，企业新招收员工的个性更加鲜明，很容易因为工作上的问题与资历较长的员工产生冲突。所以人力资源管理部门可以增加新员工和公司的领导的交流机会和渠道，让底层员工的意见能够被重视。

4.2 工程估算模型的验证

根据第3 节分析可知，试验风速范围内1.0 mm钢弹簧片稳定伞的自适应特性更优，因此以其气动特性数据作为基础数据进行拓展。即E1=209 GPa，h1=1 mm，有效的自适应变阻风速区间为V1=50 m/s～75 m/s。

根据式(4)，当弹簧片为1.5 mm 钢时，E2=209 GPa，h2=1.5 mm，则可估算出有效的自适应变阻风速区间为V2=91 m/s～137 m/s。从图11 中1.5 mm 钢弹簧片稳定伞的阻力曲线可知，当风速到达80 m/s 时，当地阻力斜率明显减小，可预测之后阻力将会进入到相对稳定的阶段，与估算结果一致。

当弹簧片为1.0 mm 钛合金时，E2=110 GPa，h2=1 mm，则可估算出有效的自适应变阻风速区间为V2=37 m/s～55 m/s。从图11 中1.0 mm 钛合金弹簧片稳定伞的阻力曲线可知，其有效自适应变阻风速区间约为40 m/s～60 m/s，与估算结论基本吻合。

以上分析验证了工程估算模型的合理性。

4.3 工程估算模型的应用

试验后观察弹簧片外形发现，在试验风速范围内，各弹簧片均未发生明显塑性变形。但是若风速继续增大，载荷也将持续增加，弹簧片极有可能发生塑性变形，而钛合金的材料屈服强度远大于钢，材料性能更优，因此以钛合金材料为例，根据式(4)，设计工程适用的自适应变阻稳定伞，使其适用的加油飞行速度和阻力值能满足真实的加油需求。

取钛合金弹簧片厚度为2.0 mm，即E2=110 GPa，h2=2 mm，由式(4)可估算出有效的自适应变阻风速区间为V2=103 m/s～154 m/s。

FD=ρV2CA/2

由于阻力值，1.0 mm 钢弹簧片稳定伞在V1=50 m/s～75 m/s 范围内阻力值约为400 N，则2.0 mm 钛合金弹簧片稳定伞在V2=103 m/s～154 m/s 范围内对应的阻力值约为1700 N。

4.4 意义及下一步研究方向

虽然实际的弹簧片受载并不是集中载荷而是分布载荷，弹簧片的受力分析和变形也要复杂得多[18]，但本文所获得的研究成果对于进一步开展工程适用的自适应变阻稳定伞研究具有重要意义。一方面，验证了所提出的自适应变阻稳定伞设计方法的正确性；另一方面，已获得的弹簧片参数、变形数据以及提炼出的工程估算模型可为弹簧片材料结构参数的设计选取提供重要的数据参考。

下一步工作中将继续结合低速和高速风洞试验，开展钛合金或其他材料弹簧片的气动特性及变形研究，进一步优化弹簧片外形、尺寸等结构设计，以提高自适应变阻力特征稳定伞的安全性和使用范围。

5 结论

本文基于骨架弹簧片原理，设计了一种全新的自适应变阻力特征加油稳定伞，并通过风洞测力试验和变形测量技术研究了弹簧片弹性模量和厚度参数对其气动特性的影响，验证该设计方法的正确性。研究结果表明：

(1)在30 m/s～80 m/s 风速范围内，8.0 mm 钢弹簧片稳定伞保持刚性状态，未发生变形，表现出恒定阻力特征的特性，阻力值随风速增加迅速增大。

(2) 1.5 mm 钢、1.0 mm 钢和1.0 mm 钛合金弹簧片均随风速变化发生自适应变形，使得稳定伞的阻力特征面积能够自适应调整，起到稳定阻力大小的作用，且抗弯刚度越小变形越大，风速越大变形越大；其中1.0 mm 钢弹簧片稳定伞的自适应特性更优。

(3)自适应变阻力特征稳定伞的动态稳定性明显优于传统恒定阻力特征稳定伞，尤其是骨架弹簧片为1.0 mm 钢和1.0 mm 钛合金时，稳定伞的阻力特征动态测量数据波动及离散标准差值显著降低，表明稳定伞的自适应特性对于提升阻力稳定性十分有利。

(4)本文所提出的自适应变阻设计方法正确合理，所获得的研究结果和工程估算模型能为工程适用的自适应变阻稳定伞设计提供重要的数据支撑。