基于阈值筛选的室内定位优化算法
柴晨境,刘 宾,潘晋孝
(中北大学信息与通信工程学院,山西 太原 030051)
0 引 言
为了满足人们的需求,改善人们的室内体验,室内定位技术在现代通信服务与应用中的重要性与日俱增[1]。近年来,随着物联网和互联网技术的发展,传统的测距定位方法如蓝牙(Bluetooth)[2]、超声波[3]、GPS[4]、WiFi[5]定位都存在一定的局限性[6]。超宽带(UWB)定位方法是近些年来一项区别于固有通信技术的技术。在传统通信技术中,传送数据是使用载波的[7],而超宽带技术则不需要,它是以纳秒或更短的时间发送和接收极窄的脉冲来传输数据,带宽为千兆赫兹(GHz)。它具有传输速率快、功耗较小、系统容量大、定位准确、穿透能力强等优点[8],因此超宽带定位方法在室内定位方向具有广阔的发展前景。
UWB常用的定位算法有基于信号接收强度(RSS)[9]、到达时间(TOA)[10]、到达时间差(TDOA)[11]、到达信号角(AOA)等方法[12]。而TDOA定位算法因为其系统复杂度低、定位精度较高、只要求基站之间的时间同步等优点,成为比较常用的定位算法[13]。
现有国内外最新的基于TDOA的UWB定位技术一般有以下3种针对传统的TDOA算法定位不精准及非视距(Not Line of Sight, NLOS)误差对移动的定位标签定位精度影响较大的解决方案:1)首先利用最小二乘方法对标签位置进行解算,然后使用改进后的滤波算法对初始位置滤波;2)在传统算法解算目标位置的基础上,针对多径误差或非视距误差使用误差抑制算法,从而降低误差对定位精度的影响;3)通过神经网络算法对数据集进行训练,形成神经网络,从而解算出较精确的标签位置。本文在基于Chan算法和粒子群算法2种常规算法的基础上增加阈值判断的坐标筛选算法,降低了粒子群算法的数据冗余度,也减少了最后得到的误差较大的坐标位置信息;经过仿真实验和实际场地实验的验证,所提出的算法定位效果较好,适于在室内非视距环境下定位的使用。
TDOA定位优化算法导致定位误差的关键因素是系统软件的随机测量误差和非视距自然环境中引入的测距误差。前一类影响因素对总定位精度误差的危害相对较小,而第2类非视距误差是定位精度误差的主要来源。
视距(Line of Sight, LOS)环境是当2个基站之间没有物体遮挡时,信道模型为LOS。因为其信号衰减少,所以跟NLOS信道相比,LOS信道模型的信号质量更好,信号吞吐量更大。NLOS误差是由于室内环境复杂,且基站与基站之间有较多物体遮挡,使信号受到除了衰减,还会受到反射、衍射、穿透等损耗。目标和锚点之间的大部分链路也会受到非视距(NLOS)偏移的影响[14]。非视距环境相比视距环境,其引起的额外时延对定位精度的影响很严重。UWB信号在穿透普通的砖墙时,信号会衰减大概一半,所以穿透墙体引起的信号传输时间的变化会极大影响定位精度。因此减小非视距误差对定位精度的影响是室内非视距环境下定位算法研究的重要课题。由于非视距环境无法改变,所以研究合适的算法来抑制或者削弱由于非视距环境产生的非视距误差也是研究的重点和难点。
本文首先简介TDOA定位模型,描述TDOA测量值的获取方法;然后在研究Chan算法和粒子群算法的基础上,利用Chan算法获得定位标签的初始坐标,随后设置阈值筛选位置坐标,再作为粒子群算法的初始值进行迭代优化。通过对2种算法和协同定位算法在LOS和NLOS环境下的定位性能进行仿真分析和实际实验环境的实验验证,可得出提出的协同定位算法可以有效减弱NLOS误差影响的同时,提高室内定位精度,满足室内定位和实际应用的需要。
1 TDOA定位模型
1.1 TDOA定位方法
在室内定位中,TDOA定位方法的基本原理是在TOA定位方法的基础上改进而来的。TOA定位是获取标签信号到达各个基站的时间得到距离来明确标签的坐标位置。TDOA定位主要采用以下2种方法:1)应用互相关技术,即对一个基站接收到的标签信号与另一个基站接收到的标签信号进行互相关运算[15],获得TDOA的准确测量值;2)根据标签信号到各个基站的到达时间差,乘以光速得到距离差,再建立双曲线模型来计算标签位置的坐标[16]。第1种方法需要严格的基站数据同步,但是在实际定位中,标签和定位基站之间很难达到完美的时钟同步,这样就在NLOS误差之外额外给定位精度增加了难度;而第2种方法不需要基站和移动标签遵循严格的时钟同步,克服并减少了系统中的时钟同步需求,适用于本文所研究的抑制NLOS误差的定位优化算法。
1.2 TDOA定位模型
TDOA定位是利用移动标记(MS)发出的数据信号与2个定位通信基站(BS)之间的时间差进行精确定位的一种方式。因为在实际应用中,单边时间难以准确测量。根据信号到达各个UWB定位基站的时间差,测量信号与各个定位基站的距离差,然后以定位基站为焦点,用距离差作为长轴作出双曲线模型[17]。双曲线的交点是定位标记位置。TDOA定位模型如图1所示。
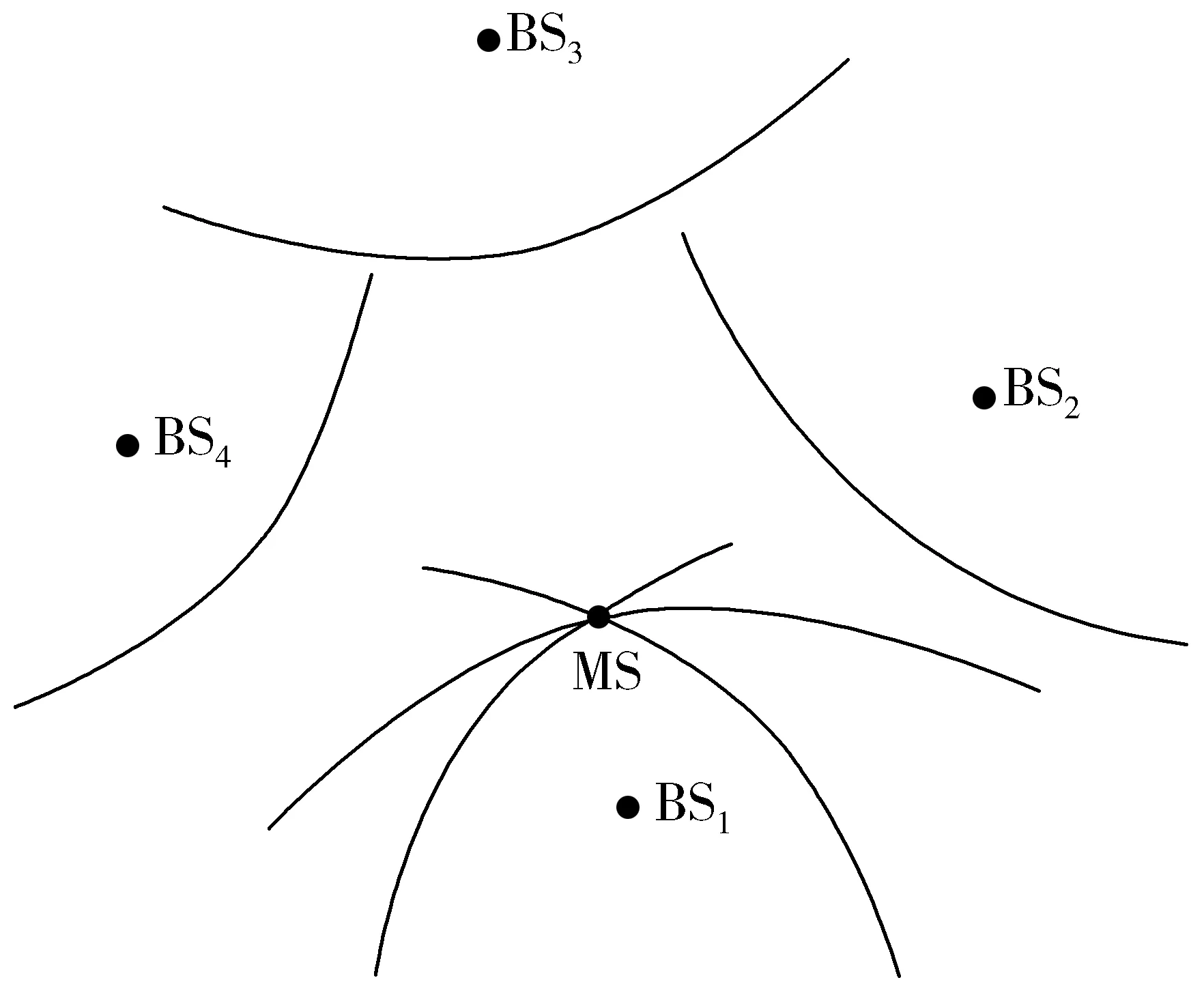
图1 TDOA定位模型原理图
每增加一个基站,就会多获得一组双曲线。仅考虑在二维平面下基站数目M≥4的情况。定位基站的坐标已知分别为BSi(xi,yi),i=1,2,…,M,设待测定位标签的坐标为MS(x0,y0),定位标签MS的信号到定位基站BS1的时间为τ1,到BSi(i=2,…,M)的时间为τi。τi,1为定位标签到2基站的时间差,c为光速。将基站1设为参考基站,实现与上位机的实时通讯。则TDOA的算法表达式为:
cτi,1=|c(τi-τ1)|
(1)
其中,i=2,…,M。解以上方程组,则可得到TDOA定位方法下的标签坐标。在视距环境中,求得的坐标即为标准的标签坐标。然而,非视距误差、多径误差干扰等要素会影响在特定的室内环境下获得的定位标签坐标的精度。因此,在Chan算法和粒子群算法的基础上,本文研究一种增加了阈值筛选[18]的混合定位算法,以进一步减弱非视距误差的影响,提高室内非视距环境下UWB定位系统的定位性能。
2 定位算法
2.1 Chan算法
在基于TDOA的定位系统中较常使用的解算算法为Chan算法[19]。在仅考虑二维平面的情况下,Chan算法可分为2种类型:仅3个定位基站参与定位;4个或更多定位基站参与定位。当Chan算法处于室内无障碍无遮挡环境且参与定位的基站数量不少于4个时,计算的定位标签坐标可以满足克拉美罗下界(Cramér-Rao Low Bound, CRLB)[20]。Chan算法的缺点是对室内空间分布的要求较高,如果空间中存在较大范围的遮挡或者室内环境就是NLOS环境时,则会对定位精度产生很大影响。本文在基于保持足够定位精度的基础上,着重研究4个及4个以上的定位基站参与定位的情况。
Chan算法是一种在TDOA测量值的基础上解算定位标签坐标的算法。Chan算法首先把TDOA方程组转换为线性方程组,其次执行第1次加权最小二乘运算[21]以获得第1次结果,然后再次执行最小二乘估计和约束以获得最终定位标签坐标。将定位标签的位置坐标设置为(x0,y0),定位基站的坐标设置为(xi,yi),定位基站到定位标签的距离为li,1号基站与第i个基站到定位标签的距离差为li,1。则由式(1)可得:
(2)
li,1=li-l1
(3)
式(2)可化为:
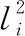
(4)
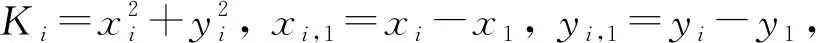
(5)
由式(3)可得:
(6)
将式(5)代入式(6)中化简可得:
(7)
此时在式(7)中,l1、x0、y0未知,xi,1、yi,1、li,1、Ki均已知,且消除了未知的标签坐标的平方项,只保留了一次项,将非线性方程组转换为了线性方程组。设:
z0=[x0,y0,l1]T
则式(7)可化为h=Gz0。在实际定位中,定位标签位置信息会受到TDOA测量噪声误差影响。引入误差向量ψ:
ψ=h-Gz0
(8)
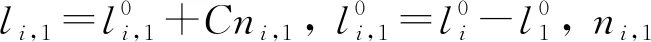
(9)
za=(GTWG)-1GTWh
(10)
误差ψ的协方差矩阵可以表示为:
Σ=cov(ψ,ψ)=E(ψψT)=C2BQB
(11)
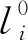
za≈(GTQ-1G)-1GTQ-1h
(12)
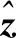
za≈(G′TB′-1GTQ-1GB′-1G′)-1G′TB′-1GTQ-1GB′-1h′
(13)

(14)

2.2 粒子群算法
粒子群算法(Particle Swarm Optimization, PSO)是由Eberhart和Kennedy在1995年提出的一种基于群体智能的优化迭代算法[22]。粒子群算法的优点是简单易实现,没有太多的参数需要调整,计算量小,收敛速度快。它是求解非线性和组合优化问题的有效方法,可用于求解本文提出的TDOA方程。利用Chan算法得到的TDOA方程解作为粒子群算法的初始位置进行更新和迭代[23],获得的最好结果即定位标签的最终位置。算法实现步骤如下:
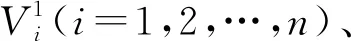
2)将粒子的参数代入式(19)得到差值和,并初始化每个粒子的个体最优位置和群体最优位置。
3)对粒子的速度与位置进行更新,更新公式如下:
(15)
(16)
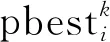
5)检查流程的结束条件,本文设置中断阈值θ和最大迭代次数N,若达到中断阈值θ则不需进行粒子群优化;若达到最大迭代数目N,则中断粒子群算法流程。若都不满足则迭代优化次数加1,算法流程转至步骤3。
3 基于非视距信息筛选的混合定位算法
3.1 设置阈值筛选非视距误差信息
在室内非视距NLOS环境下Chan算法的定位效果会大打折扣。所以为了保证室内定位系统的精准度,并且减轻粒子群算法的压力,提升系统的整体性能,需要对室内复杂环境下Chan算法解算出来的标签位置信息进行优化筛选。
由上一章中Chan算法解算得到的定位标签位置来计算其他定位基站与1号定位基站之间的距离差,即:
(17)
根据标签和2个定位基站之间的时间差计算的实际距离差为:
li,1=cτi,1
(18)
将式(17)与式(18)二者做差并求和可得:
(19)
求差值和的目的是为了考虑到每一个定位基站与1号基站差值的误差,使后续的算法计算更为准确,提升定位系统的精准度。设置合适的阈值θ与S进行比较,阈值不宜过大或过小,过大会使误差筛选范围扩大,降低定位精度;过小会使定位误差筛选过于严苛,降低定位效率。
设参考基站为1号基站,坐标为BS1(x1,y1)。其余基站坐标为BSi(xi,yi),i=1,2,…,M。设参考基站与其他基站之间的距离为d1i,则有:
(20)
根据定位系统中的天线延迟[24]标定模块,该模块主要实现对参考节点与普通节点之间天线延迟的标定。具体过程如下:
1)当PC机下发天线误差标定指定时,若为普通节点,则转为接收状态,接收来自参考节点发送的信息。
2)若为参考节点,则转到发送状态,发送天线标定信息,同时记录下发送时间戳Tref_tx后,转为接收状态。
3)普通节点接收到参考节点发送的信息后,记录下接收时间戳Tnor_rx后,转为信息发送状态,向参考节点发送应答信息,同时记录下发送时间戳Tnor_tx。
4)将这2个时间戳上传给PC机。参考节点接收到普通节点发送的应答信息后,记录下接收时间戳Tref_rx上传给PC机。
参考基站和普通基站的误差延迟分别为:
Tref_error=Tref_rx-Tref_tx
(21)
Tnor_error=Tnor_tx-Tnor_rx
(22)
则可得出普通基站与参考基站间的天线延迟误差:
(23)
其中c为光速,15.65为经查阅DWM1000芯片手册中的时钟计数器的值转换为的时间值,单位为ps。从芯片里面读出的时间戳值累加1代表15.65 ps。
将最后得出的各个普通基站与参考基站的天线延迟误差Terror_1i累加并求平均得到平均延迟误差T,单位为s:
(24)
则可设定阈值的大小为θ=Tc。当S>θ时,说明通过Chan算法解算出来的定位标签的坐标与实际坐标有较大偏差,定位信息受到了非视距环境的干扰,需要通过粒子群算法对其进行迭代优化再输出;若S<θ,则表示通过Chan算法解算出来的坐标信息较为精准,不需要再通过粒子群算法优化,可以直接输出作为最终坐标。
3.2 混合定位算法
在视距LOS环境中,Chan算法的系统测量误差仅考虑了其均值为0,也就是说,在视距LOS环境中,可以获得比较精确的标签位置坐标。然而,在非视距NLOS环境下,定位基站之间存在的非视距误差信号将产生正平均测量误差,此时的标签位置估计将有较大偏差。而粒子群算法因为计算时经过多次迭代优化可以较好地消除非视距误差对系统产生的影响,所以本文提出一种Chan算法与粒子群算法及阈值判断相结合的室内非视距环境下的混合定位算法对标签位置进行解算。
由于在非视距环境下,粒子群算法的性能表现较好,所以将经过阈值筛选过后的Chan算法求得的标签位置坐标代入粒子群算法优化,可以更好地提升算法性能。混合定位算法流程如下:
1)首先测得在室内非视距环境下布好的基站位置坐标BSi(xi,yi),i=1,2,…,M。通过分别测量定位标签到参考基站和其他基站的信号到达时间差计算出距离差li,1。
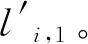
3)设置阈值θ,将步骤1和步骤2中求得的2个距离差做差求和得到差值和S,将差值和S与阈值θ进行比较:若S<θ,则直接输出标签位置坐标;若S>θ,则进行下一步。
4)通过粒子群算法对式(19)进行求解,将与实际位置有较大偏差的标签坐标位置代入式(19),通过粒子群算法进行迭代优化,直到满足算法预设的终止条件,得到标签位置的最优解再进行输出。
算法流程如图2所示。
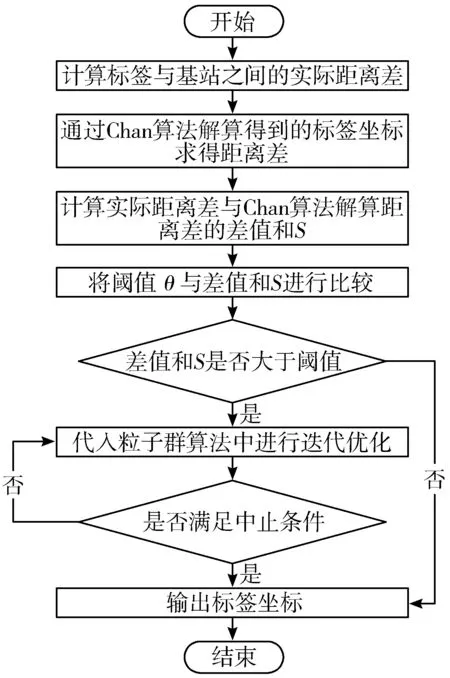
图2 混合定位算法流程图
本文提出的混合定位算法有以下优势:1)经过阈值筛选的Chan算法解算结果作为粒子群算法的初值,进一步缩小了粒子群算法的收敛范围,能更快地找到最优解;2)经过阈值筛选可以先将符合定位精度的坐标先行输出,这样可减少整体算法的冗余度,提升算法性能。
4 混合定位算法仿真及分析
4.1 定位算法精度评判标准
1)均方根误差(RMSE)。
均方根误差即测量值与理论值差的平方与平均次数N比值的平方根[25]。在实际应用中,实际测量次数有一个上限,理论值必须由测量的最佳值取代。均方根误差对数据中的异常值十分敏锐,因此均方根误差可以更好地反映数据的精度,定位精度的高低与均方根误差的大小成反比。均方根误差可用以下公式表示:
(25)
(26)
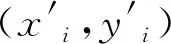
2)误差累积分布函数(CDF)。
累积分布函数是概率密度函数的积分,它表明N次定位系统测试中有限范围内NLOS错误信息的次数占所有测试次数的百分比[26],是值到其在分布中百分等级的映射。误差累积分布函数可用以下公式表示:
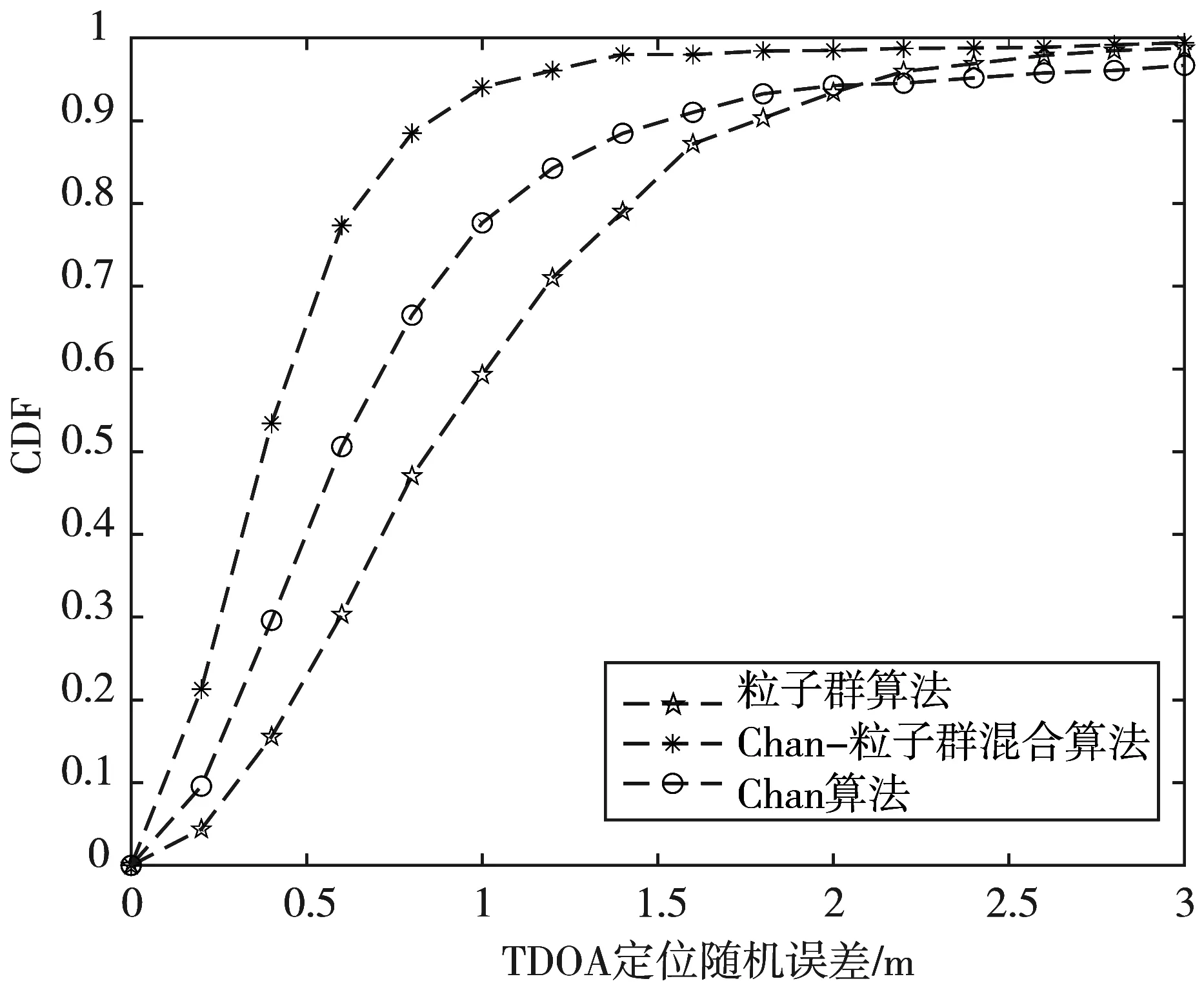
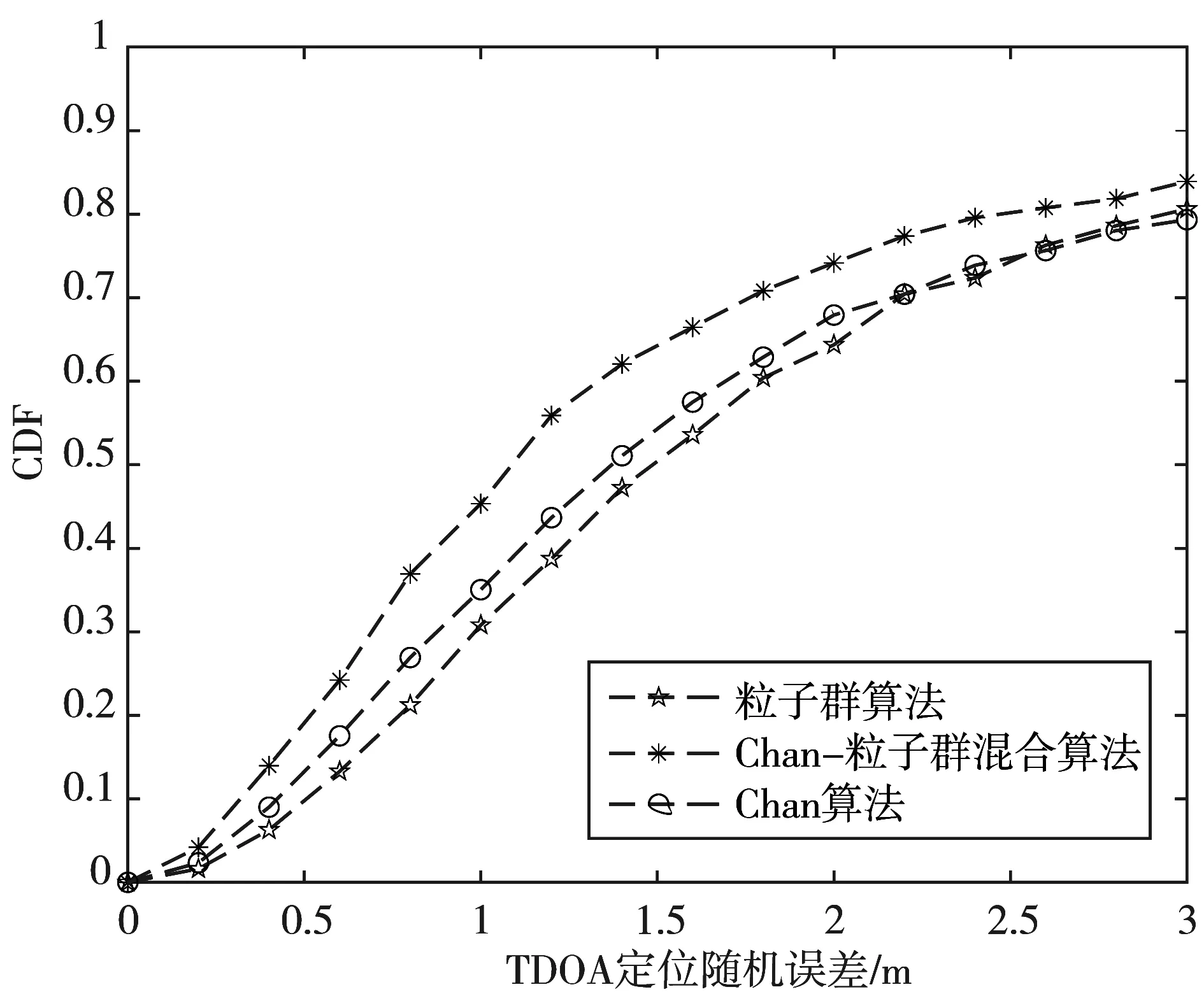
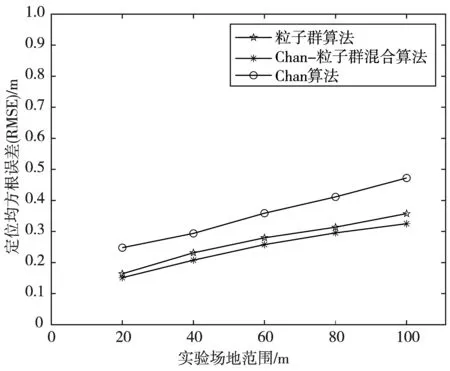
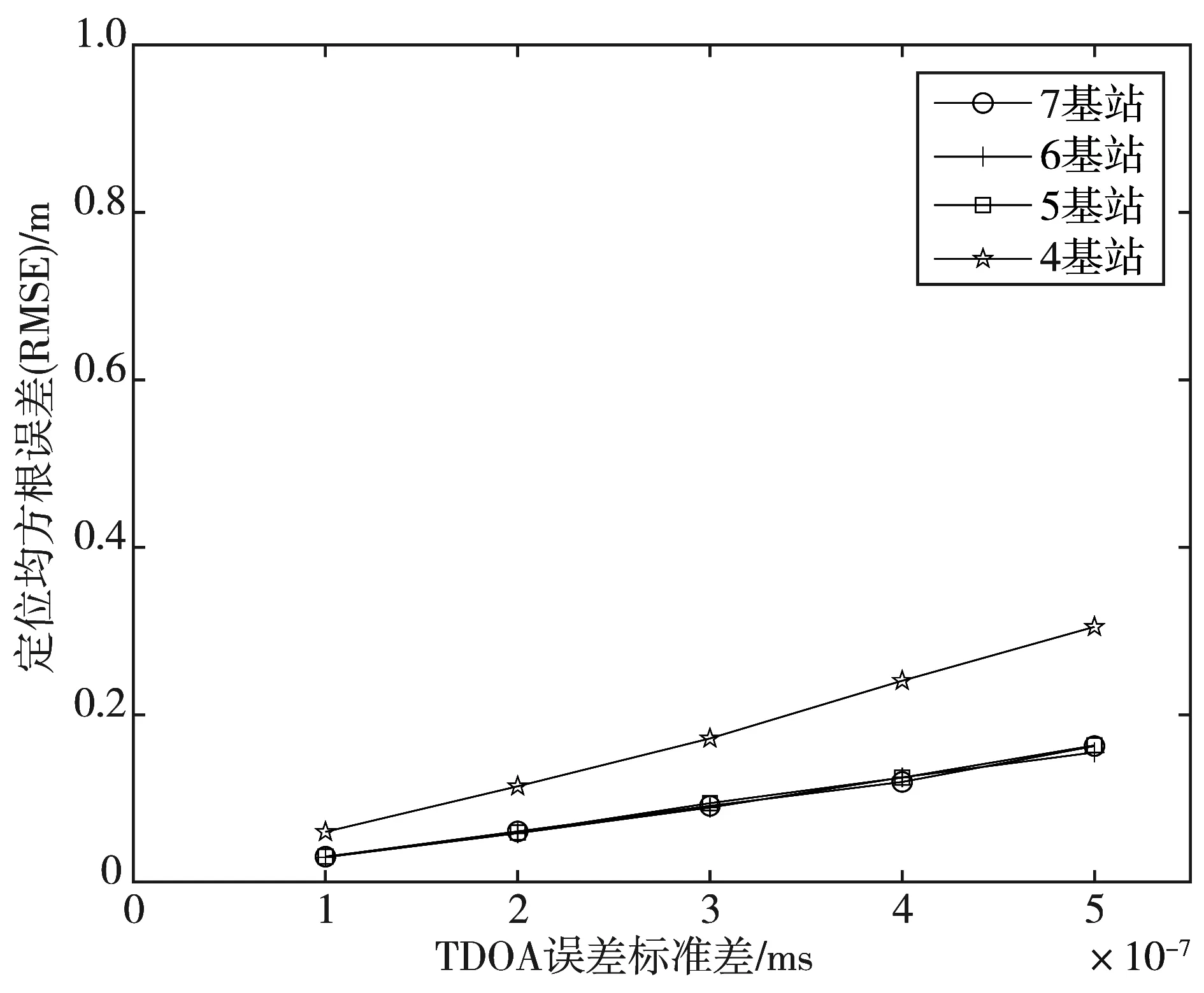
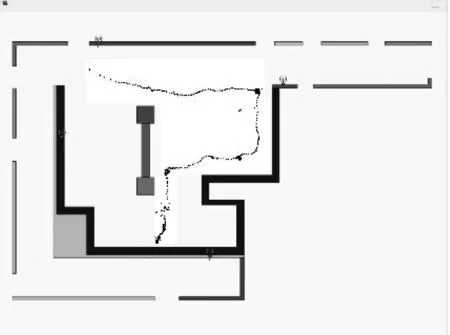
CDF=F(x)=Pr(X≤x), -∞ (27) 本文使用MATLAB2020b仿真软件对上述提到的算法进行验证。仿真环境采用45 m×45 m的二维室内空间,存在4个定位基站和一个定位标签。定位基站坐标已知,分别为(0,0)、(0,45)、(45,0)、(45,45),标签坐标为(5,10)。假设在2个相同的二维空间中存在视距环境和非视距环境,对本文提出的算法性能进行比较。 分别给LOS环境和NLOS环境添加TDOA随机测量误差[27],并分析2种环境下不同算法的CDF曲线变化。 图3与图4表示3种定位算法在视距环境下和非视距环境下的定位性能的比较。由图3可以看出,随着加入误差的增大,LOS环境下,Chan算法在定位性能上要比单一粒子群算法更好,定位精度更高;而经过阈值筛选的Chan-粒子群混合算法表现出了更高的定位性能。图4表示在NLOS环境下,单独的Chan算法与粒子群算法相比较,定位效果差别不大,CDF曲线趋势大致相同;而Chan-粒子群混合算法通过Chan算法解算结果作为初始值,并且经过阈值筛选之后再通过粒子群算法的迭代,优化了单一Chan算法在NLOS环境下定位精度不高的缺陷,定位性能更高,在定位精准度上都比单一算法要更加有效和稳定。 图3 LOS环境算法性能 图4 NLOS环境算法性能 图5是针对不同范围的室内NLOS环境下Chan算法、粒子群算法、Chan-粒子群混合定位算法的定位性能比较。可见,在NLOS室内环境中,Chan-粒子群混合定位优化算法的定位实际效果最好,且Chan算法计算的标签位置误差大于其他2种算法。原因是Chan算法假设噪声误差服从理想的高斯分布,因此其在非视距环境中的性能将比其他算法产生更大的影响。同时随着实验场地范围的扩大,3种算法的定位误差都相应增大,但是误差增幅都较平缓,说明提出的混合定位算法较符合一般范围的室内环境应用。 图5 3种定位算法在不同范围的NLOS室内环境定位误差对比 图6和图7比较了Chan优化算法和Chan-粒子群混合优化算法在室内NLOS环境下4~7个通信基站标准下的定位性能。当TDOA偏差为0.1、0.2、0.3、0.4、0.5 ns时,分析2种算法的定位误差。可以看出Chan-粒子群混合算法的总体定位误差较小;同时可以看出,当有4个以上的基站时,2种算法的定位均方根误差显著降低;但当有5个以上的基站时,定位精度不再显著提高。所以在保证定位精度的前提下,在一个室内区域内选择5个定位基站效果最好且控制了成本。 图6 Chan算法定位性能 图7 Chan-粒子群混合算法定位性能 实验环境选用了11.12 m×10.9 m大小有遮挡的室内实验室环境,分别布设4个定位基站A1(1.874,4.764)、A2(0,0)、A3(7.532,-6.038)、A4(11.248,2.711)。 图8为实际实验场地环境,将实验场地CAD格式的地图坐标导入由QT程序编写的上位机服务器界面,手持定位标签分别在固定路线下测试在仿真环节出现的3种定位算法。 图8 实验场地环境 图9~图11为3种定位算法在复杂非视距办公室环境下的定位标签行进轨迹图。在4个基站分布的范围中,基站与标签发出的信号会受到墙体和柱墙的遮挡及削弱。图9和图10分别为Chan算法和粒子群算法的标签行进轨迹,可以看出,在多个基站信号被遮挡的区域,行进轨迹出现了明显的波动,并且周围会出现与实际位置相差较大的点。由图11可以看出,提出的基于阈值筛选的混合算法行进轨迹更为平滑,歧点[28]较少,有效减弱了非视距误差对定位结果的影响,并且在一般遮挡的室内环境下都较为适用。 图9 粒子群算法定位标签行进轨迹图 图10 Chan算法定位标签行进轨迹图 图11 Chan-粒子群混合算法定位标签行进轨迹图 本文对室内非视距环境下的算法进行了研究。首先通过Chan算法进行2次加权最小二乘法求出初始标签位置坐标;然后再设置合适的阈值与距离差的差值和进行比较,将大于阈值的结果通过粒子群算法迭代优化后再输出,小于阈值的结果直接输出,有效增加了系统的运算速度和系统性能。通过计算不同CDF值的TDOA误差平均值,本文提出的Chan-粒子群混合定位算法相比单一Chan算法定位精度提升了27%,比单一粒子群算法提升了31%。仿真结果和实际场地测试结果表明,基于阈值筛选的混合定位算法可以比较好地抑制非视距误差对系统的影响,提升了室内非视距环境下的定位精度。4.2 混合定位算法仿真及分析

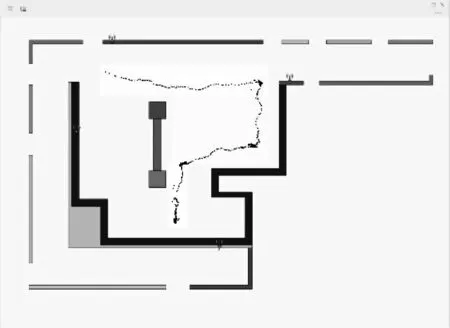
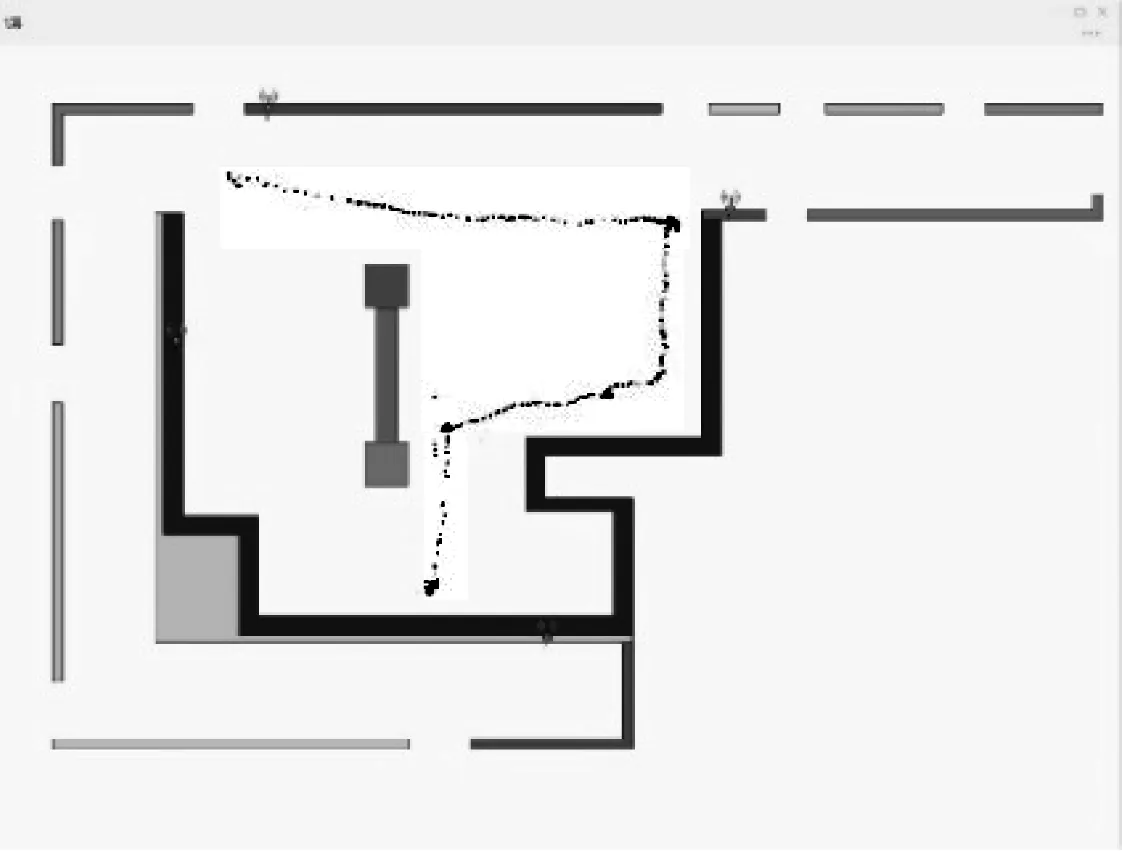
4.3 定位算法实际场地实验

5 结束语

