降雨型浅层黄土滑坡危险性评价与区划
——以山西柳林县为例
李艳杰,唐亚明,邓亚虹,宋焱勋,慕焕东,山 聪,崔思颖
(1.长安大学地质工程与测绘学院,陕西 西安 710054;2.中国地质调查局西安地质调查中心,陕西西安 710054;3.西安理工大学岩土工程研究所,陕西 西安 710048)
0 引言
黄土高原山区地形结构破碎、沟壑纵横、土质疏松、水土流失严重,特殊的地形地貌条件及土体类型使黄土高原地区成为目前我国自然地质灾害最为发育的典型地区之一[1]。据悉,我国每年发生在黄土高原的地质灾害占比高达30%,严重制约着我国黄土高原地区的新型城镇化各类工程建设,危及公路、铁路、水利等重大基础工程的安全运营。由于发育于黄土高原的黄土是一种大孔隙且多具有湿陷性的特殊性质的土,其在遇水后力学强度迅速降低。因此,在黄土高原地区降雨诱发地质灾害频发[2−3],尤其是降雨诱发的浅表层滑坡地质灾害最为频发。据统计,黄土高原中地质灾害的75%以上触发于降雨条件下[4]。近年来,受极端天气的影响,黄土高原强降雨频发[5],使得浅表层黄土滑坡广泛发育,浅层滑坡已成为黄土高原最危险的地貌之一[6]。因此,对降雨作用下黄土斜坡稳定性分析与评价具有重要的理论实际意义。
一般从单体和区域两方面,对斜坡的稳定性进行评价[7−8]。目前,已经有很多的方法被应用于模拟计算单体斜坡的平均稳定性[9−11],然而单体斜坡的稳定性评价,主要针对某一个具体的地质剖面,在时间尺度上对灾害进行预报,适用于滑坡工程治理。斜坡的不稳定地质灾害通常具有突发性、群发性、分布广、隐蔽性等特点。因此,区域斜坡稳定性分析对地区的土地规划和减灾防灾更加具有参考价值。研究表明,初步从区域稳定性进行宏观把控,在空间尺度上判断灾害发生的危险性,对于可能会失稳的区域,进行重点监测和防治,精准施策,使危险较高的地段得到保护和实施措施,实现资源最大化利用,有助于保护人民的生命财产安全[12]。
为了对区域斜坡稳定性进行分析,大量的定性和统计方法已经被用来进行模拟预测,例如模糊数学法[13]、层次分析法[14−15]、信息量法[16−17]、支持向量机[18−19]、回归模型[20−21]、人工神经网络[22]和证据权模型[23−25]等。其中定性分析法具有较大的人为主观判断因素;统计模型的研究方法只考虑历史中地质灾害事件出现的频数,不深入考量灾害发生的内在机制,不以明确的力学过程作为基础,所得的稳定性评价结果只适用于某个具体的区域。一些学者从关注滑坡机理的角度出发,提出了一些结合滑坡机理的定量评估的物理模型,如SHALSTAB[26−27]、SINMAP[28−29]、TRIGRS[30−31]、SCOOPS3D[32−33]等。上述这些模型在评价边坡稳定性方面基于物理模型并将影响边坡稳定的因素定量化来计算安全系数,具有明确的力学过程作为基础,减少了人为主观判断因素等优势。
柳林县境内80%以上是黄土梁峁区。据统计,柳林县所发生的地质灾害基本分布在黄土梁峁区,且多为强降雨诱发的浅层黄土滑坡。文中基于SINMAP 模型,以柳林县为研究对象,对研究区不同降雨条件下的区域斜坡稳定性做了对比分析。希望通过对降雨条件下柳林县的浅层黄土滑坡危险性评价的预测研究成果,为柳林县土地规划和减灾防灾提供参考。
1 研究区概况
研究区位于山西省中部西侧,吕梁山西部。该区域属于典型的温带大陆性干旱-半干旱气候,6—9月份是降雨聚集时间段,全年总降雨量的67.5%基本产生在此时间段。据历史统计,柳林县的降雨量,年峰值为632 mm,多年雨季平均日降雨量的峰值为45 mm,日峰值为91 mm,时峰值为49 mm,多年平均为494 mm,年平均蒸发量为1 901 mm[34]。
柳林县位于吕梁山区西部,区内沟壑纵横,山峦起伏,整体上呈东北高、西南低的地形。黄土梁峁区约占80%以上。海拔700~1 300 m,地形陡峻,河流侧蚀严重,这使得该地区很容易发生滑坡等地质灾害。在地貌上,柳林县所发生的地质灾害基本上分布在黄土梁峁区。其中,刘家山、成家庄、东洼、龙门垣、下罗候一线以西,基本上以黄土丘陵区为主,黄土沟谷区主要分布于黄河东岸及其各支流等较大沟谷中[34]。
区内出露地层中太古界河口群主要分布于县内北部大雨梁、王家会村一带;古生界寒武系分布于县东北部杨家岭一带;奥陶系分布于县东部溶蚀、剥蚀区;石炭系和二叠系主要分布在境内中、东部广大地区;中生界三叠系分布于沟谷中;新生界上新近系分布于境内屈产河、三川河等河谷两侧,第四系分布于黄土梁峁区及屈产河、三川河等河谷中。区内构造较为简单,整体上呈由北东向南西渐倾的单斜构造,构造形迹主要为断裂、褶皱。
由区内含水介质的主要岩石分类结构特征和地下水主要赋存的环境条件可知,区内地下水分为五大类。其中,松散岩类孔隙水广泛分布于黄土梁峁区、三川河及黄河支流河谷;碎屑岩类裂隙水主要分布于柳林县中西部的黄土沟谷区;碎屑岩夹碳酸盐岩裂隙岩溶水分布于柳林县成家庄—龙门塔一线及广大的中西部地区;碳酸盐岩岩溶水分布较广,遍于柳林县;变质岩类裂隙水较少,仅在柳林县东部杜家岭、王家会一带小面积分布(图1)。
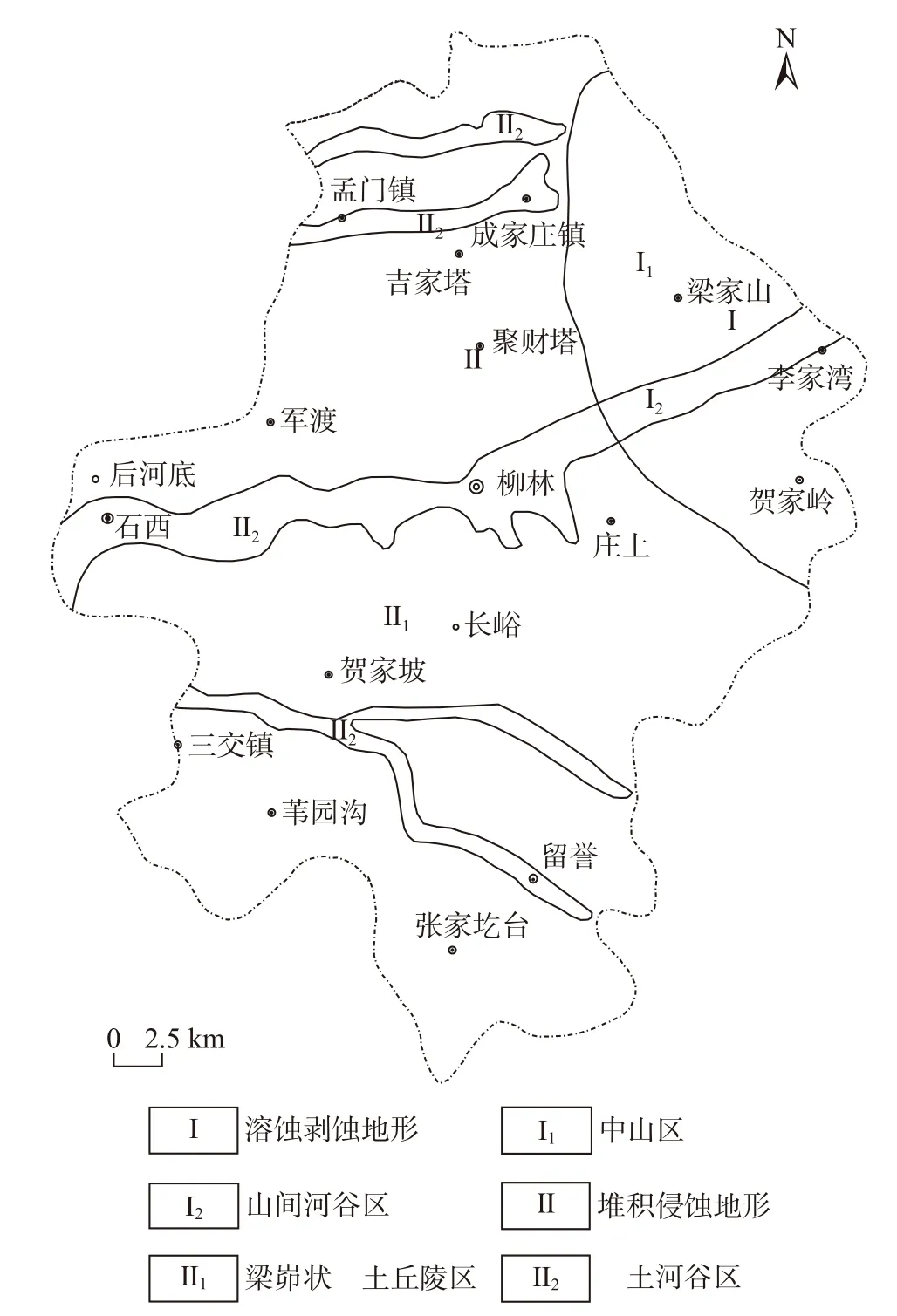
图1 山西省柳林县地貌分区图[34]Fig.1 Geomorphological zoning map of Liulin County,Shanxi Province
境内主要河流为三川河、屈产河,均属黄河流域。屈产河属黄河一级支流,发源于石楼县最南端,向北经柳林县汇入黄河,境内长12.8 km,流域面积约109.6 km2;三川河是横贯县东西的一条大河,发育于方山县、离石市和中阳县,长70.4 km,流域面积约558.1 km2;黄河在县境西界由北向南,长约56.7 km,年平均流量397.3×108m3。
2 SINMAP 模型的应用
2.1 基本原理
Pack 等[35]基于无限斜坡稳定性模型和稳态水文模型建立了SINMAP 模型,并将稳定指数(SI)作为输出结果,对研究区的斜坡稳定性进行评价。该指数的定义为假设参数在不确定性范围内均匀分布,地表斜坡处于稳定状态的概率,即SI=Prob(FS>1)。
2.1.1 地形湿度指数w
采用稳态水文模型估算地形湿度指数w,地形湿度指数的上限为1,如果值大于1,则会在地表形成径流,可定义为:
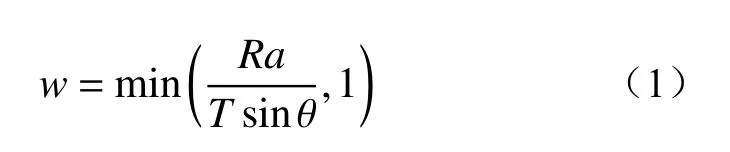
式中:R——稳定状态时的流量/(mm·d−1);
a——单位汇水面积/m2;
T——导水系数/(m2·d−1);
θ——滑面倾角/(°)。
式(1)中R为关键时期触发滑坡所需的有效补给,而不是长期(例如年)平均补给量。SINMAP 模型出于综合考虑气候和水文地质因素的影响,把R/T视为单个参数来量化相对湿度。
2.1.2 无限斜坡稳定性模型
为了定义稳定性指数Stability Index(SI),式(1)中的湿度指数被并入式(2)所示的无量纲安全系数中:
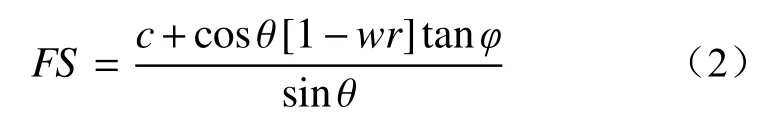
变量a和θ是由数字高程模型(DEM)计算获取的。密度比r用来描述水和密度之间的关系,一般规定为定值。SINMAP 模型中的一些输入参数,如c、tanφ和R/T,通过设置最大和最小阈值,来允许变量的不确定性。输入参数在阈值之间的随机变化会生成地表稳定性的概率分布。
假设R/T=x,tanφ=t,上下限均匀分布为:
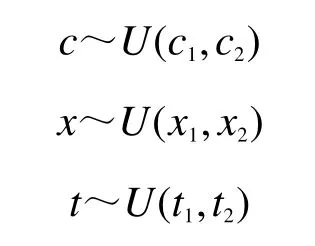
对于斜坡稳定性最不利的(最保守的)参数组合为在c、x和t的分布上,当c=c1、t=t1和x=x2时。在这种情况下,理论上得到的安全系数FS(FSmin),为参数不确定性组合中能够计算出来的最小值。在此条件下,如果FS>1,则该区域是无条件稳定的,SI定义为:
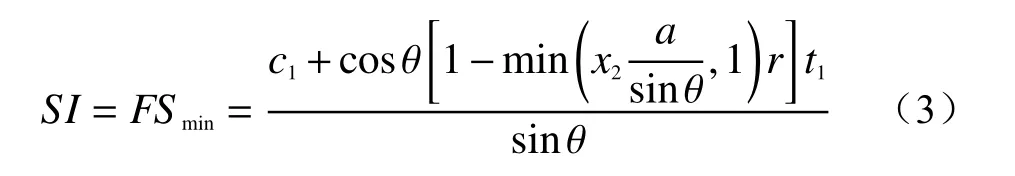
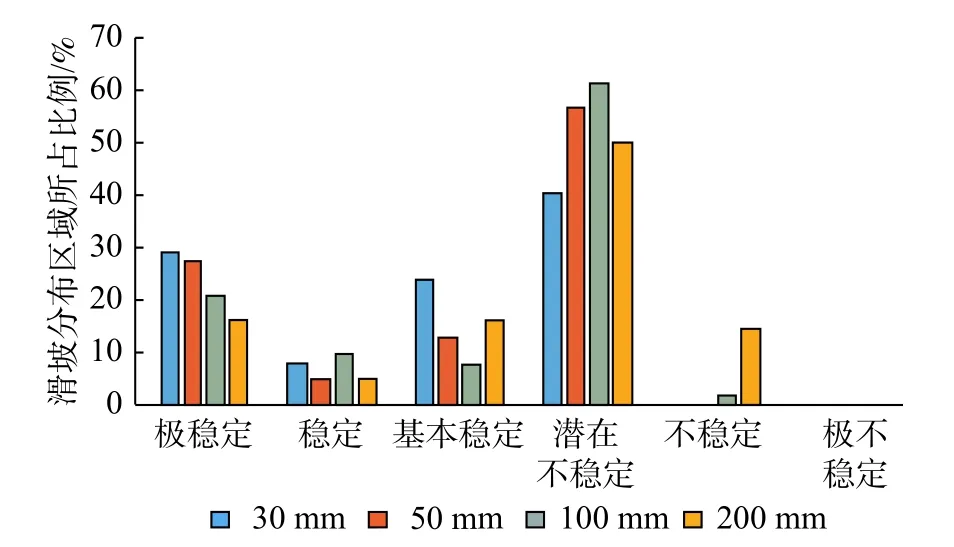
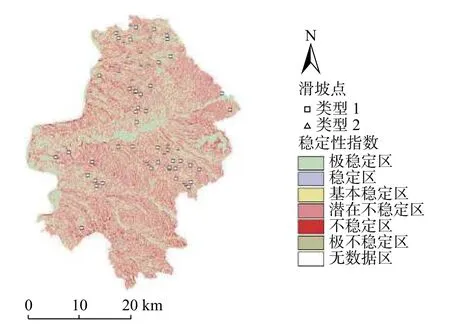
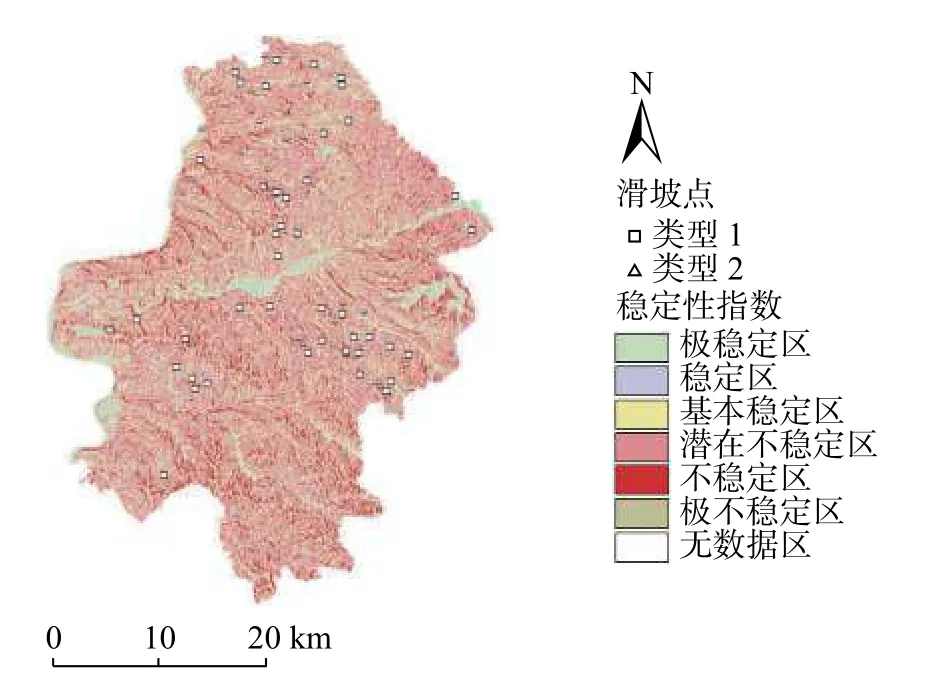
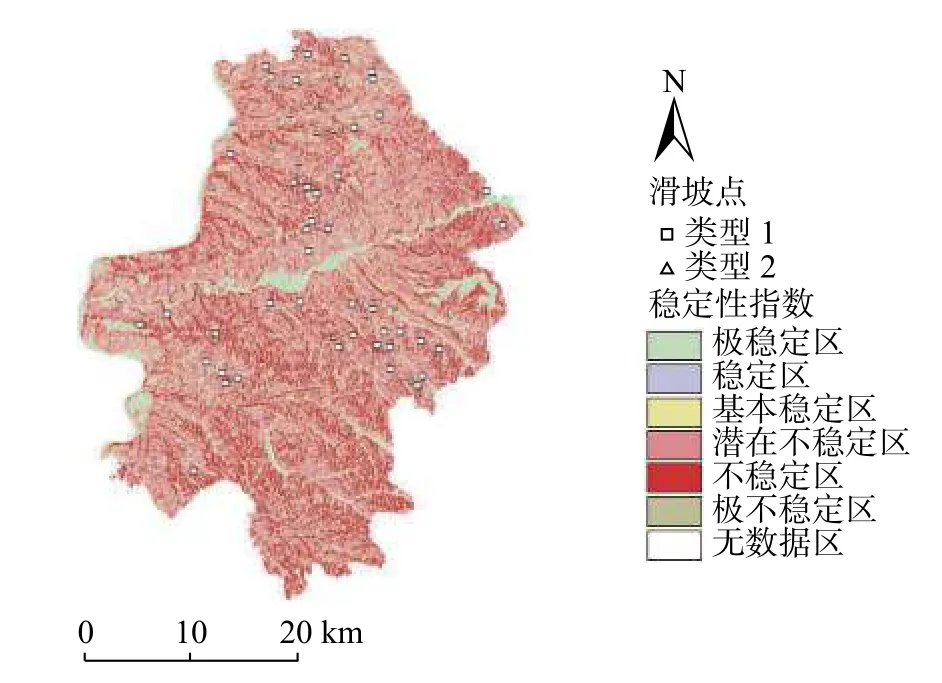
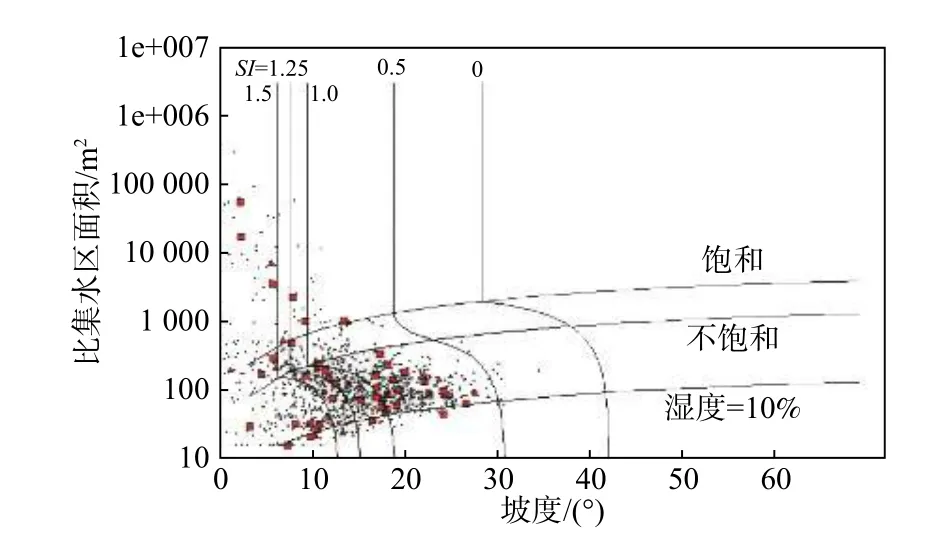
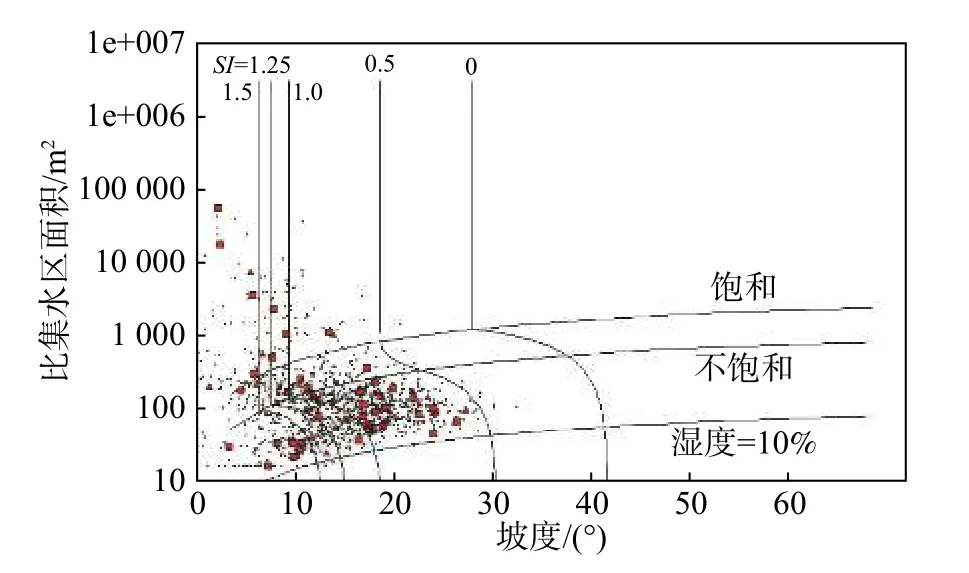
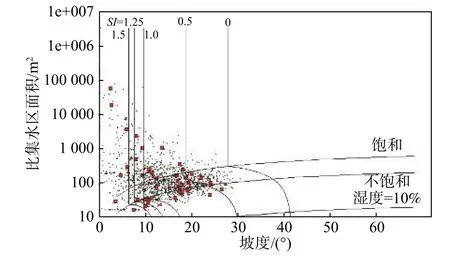
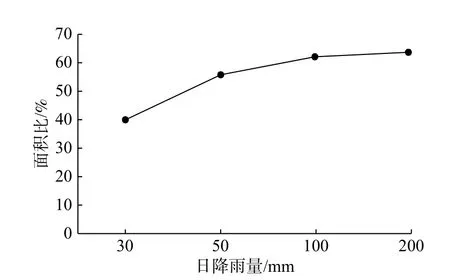
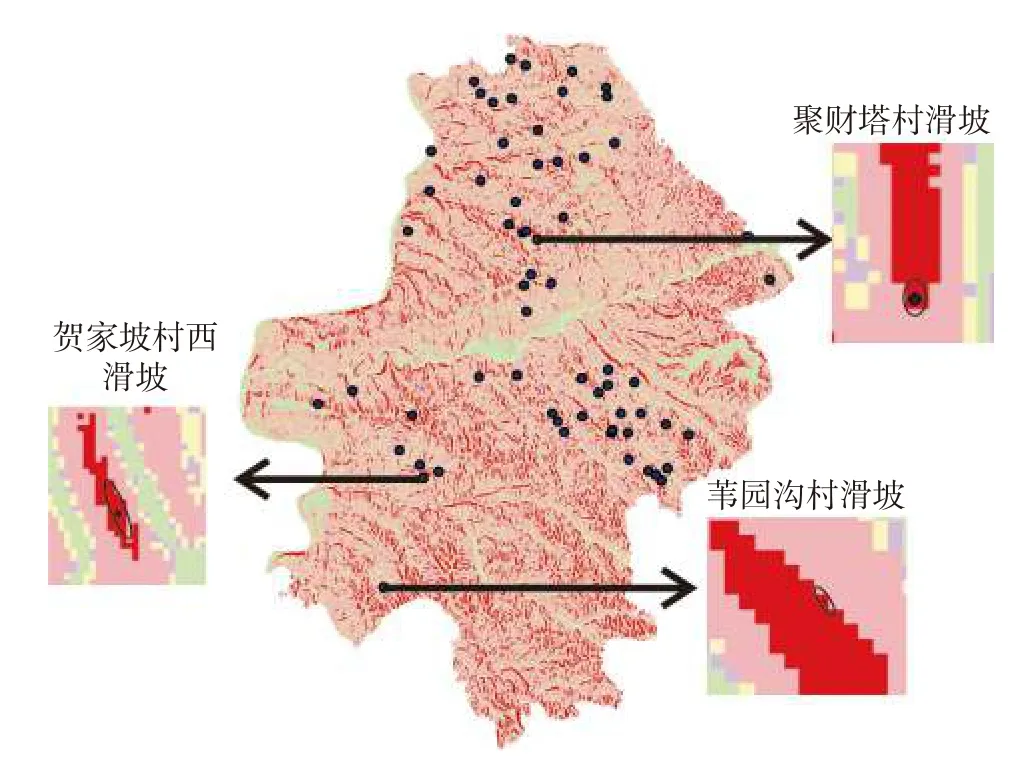
最小安全系数值低于1 的地表斜坡,存在变形失稳的概率,也就是说当FSmin<1,FSmax>1时,该斜坡存在变形失稳的概率,此时,0 对于斜坡稳定性最有利的参数组合为在c、x和t的分布上,当c=c2、t=t2和x=x1时。在这种情况下,理论上得到的安全系数FS(FSmax),为参数不确定性组合中能够计算出来的最大值: 当FSmax<1时,视为该处地表坡处于不稳定状态,那么SI=Prob(FS>1)=0。 选取柳林县分辨率为30 m 的数字高程模型(DEM),基于土壤类型、地质、地形地貌和气候水文等资料,结合研究区内分布的历史滑坡灾害点,对研究区的斜坡稳定性进行评价。已知研究区内已有的滑坡中,大型滑坡比例占1.5%,中型滑坡比例占14.4%,小型滑坡比例占30.3%。从物质成份上看,主要为土质滑坡,共占滑坡总数的92%,土体主要为松散的粉土及粉质黏土。 根据调查柳林县地质灾害大多由暴雨及以上的降雨诱发,降雨与灾害间的关系极其密切。其中暴雨型滑坡主要分布于庄上镇、成家庄镇、王家沟乡孟门镇、陈家湾乡等乡镇,滑坡共38 处,其中35 处为老滑坡,发生时间不明;其余1 处为孟门镇前冯家沟村于1976年9月发生的滑坡,2 处为王家沟乡佐主村、大圪垯村分别于1987年6月和2001年6月发生的滑坡,其全部为降雨诱发。 SINMAP 模型的计算涉及到多个参数,包括比集水区面积a、稳态时的流量(有效降雨量)R、坡度θ以及岩土体的物理力学参数,其中岩土体的物理力学参数主要包括密度 ρ、内摩擦角φ、黏聚力c和导水系数T等。首先,坡度和比集水区面积数据由DEM 高程数据计算得出。其次,土的抗剪强度参数和密度是通过野外采取的土样进行室内试验获得。最后,对于稳态时的流量(有效降雨量)R和导水系数T,因导水率总是远大于稳态时的流量,亦即R/T的值较小。因此,在分析地形湿度指数w的空间分布情况时,采用了不同的T/R进行试算。研究发现,在T/R= 3 000 时,大于1 的地形湿度指数分布情况与柳林县的水系分布相似。因此,由多年雨季平均日最大降雨量(45 mm),采用反演分析法[36]计算土体的导水系数。根据野外采取的土样获得的室内实验结果,结合已有的数据资料,选取以下参数(表1)。 表1 模型选取的参数值Table 1 Parameter values selected by the model 根据SI的值,对研究区内区域稳定性进行分类,可以分为6 个类别(表2)。由表2 可知,1~3 类为稳定区(FSmin>1),亦即在该区域内,即使斜坡处于最易失稳的情况,仍然保持稳定,除非叠加强降雨、地震等巨大的不稳定因素,才可能会失稳。第4 和第5 类均存在失稳的可能性(FSmin<1,FSmax>1),其中第4 类失稳的可能性小于50%,第5 类失稳的可能性大于50%,第6 类(FSmax<1)在指定参数取值范围内取任何值,这些区域都将发生失稳。 表2 稳定性分类定义Table 2 Stability classification definition 据历史统计的40年日降雨数据来看,柳林县超过50 mm 的暴雨为45 次,日降雨量超过100 mm 的大暴雨为4 次,超过20 mm 的特大暴雨为1 次[37]。因此,文中研究主要对30,50,100,200 mm/d 四种降雨量下的柳林县的滑坡变形失稳危险性进行分析预测。基本对应大雨、暴雨和大暴雨工况。通过计算得到不同降雨量下失稳面积的变化规律如图2所示,图2 中纵坐标所示的面积百分比代表各稳定分区的面积与区域总面积的比值。由图2 可知,随着降雨量的增加,研究区域内各稳定分区的面积逐渐减小,失稳分区的面积逐渐增大,表明稳定区逐渐过渡到失稳区,变化幅度为 31.6%。 图2 不同降雨量下失稳面积变化Fig.2 Changes of instability area under different rainfall 为了更直观反映不同降雨强度下不同稳定级别区域面积的变化规律,绘制不同稳定级别下区域面积随降雨强度增加的变化规律图如图3所示。 图3 不同稳定级别下区域面积变化Fig.3 Regional area changes under different stability levels 由图3 可知,随着降雨量的增加,区域内处于稳定状态的地区逐渐减少,处于失稳状态的地区逐渐扩张。具体表现为,极稳定区,稳定区及基本稳定区的面积所占总面积的比例,随着降雨量的增加均呈递减趋势,降幅分别为12.1%,7.7%和11.8%。潜在不稳定分区,不稳定分区和极不稳定分区分别占总面积的比例,随着降雨量的增加整体上均呈递增的趋势,增幅分别为20%,11.6%和0.008%。其中潜在不稳定区的面积在降雨量为100 mm/d 与200 mm/d 表现为持平,此时不稳定区面积则表现为突增的状态,说明在该区域当降雨强度达到200 mm/d 时,产生滑坡等地质灾害的概率、分布区域与危险性进一步增加。 为了量化SINMAP 模型对研究区内区域斜坡稳定性的预测结果与浅层滑坡空间分布的一致性,绘制了不同稳定性级别下滑坡分布区域面积所占比例示意图(图4)。 图4 不同稳定性级别下滑坡分布区域面积所占比例(24 h 内)Fig.4 Proportion of the area of landslides with different stability levels(with 24 h) 由图4 可知,当雨量较小时,滑坡主要产生在模拟结果中比较稳定的区域。随着降雨量的增加,滑坡所处位置逐渐由稳定状态向失稳状态发展,位于失稳分区的滑坡数量逐渐增加,且失稳分区内也存在潜在不稳定区向不稳定区的转化。当降雨量为200 mm/d 时潜在不稳定区向不稳定区转移较大,说明不同降雨强度可能会触发不同的滑坡危险程度。 基于SINMAP 模型通过输入DEM 数据、土体密度、内摩擦角等参数,结合已有滑坡灾害点分布数据,计算不同降雨量下研究区的地表稳定性指数分布图(图5−8)。 图5 30 mm 降雨地表稳定指数分布图Fig.5 30 mm rainfall surface stability index distribution map 图6 50 mm 降雨地表稳定指数分布图Fig.6 50 mm rainfall surface stability index distribution map 图7 100 mm 降雨地表稳定指数分布图Fig.7 100 mm rainfall surface stability index distribution map 图8 200 mm 降雨地表稳定指数分布图Fig.8 200 mm rainfall surface stability index distribution map 从图5−8 中可以观察到,失稳区域随降雨量的增加呈现增多的趋势。这表明当降雨量较小时,由于受到地形的影响,失稳分区主要分布在雨水汇集的黄土沟谷区。随着降雨强度的加强,失稳分区逐渐向山脊和坡度较缓的斜坡单元扩展。在地表稳定指数分析的基础上,基于SINMAP 模型,模拟得到不同的降雨量下研究区内坡度-比集水区面积图(图9−12)。从图9−12 中可以观察到,饱和、非饱和以及10%的湿度分界线,当日降雨量增大时,均呈现了向下移动的趋势。这表明,研究区内的饱和程度,随降雨强度的加强而增长。研究发现,失稳分区中的滑坡点和用小黑点示意的研究区中的随机区域占总体的比例,同样伴随着降雨量的增加而出现了递增的趋势。具体表现为,分布在稳定区中的滑坡点和小黑点逐渐向失稳区扩展。由于地形的影响,当研究区内降雨量较小时,滑坡主要分布在雨水汇集的黄土沟谷区。随着降雨量的增加,区域内斜坡稳定性也随之降低,失稳地区逐渐由沟谷区向沟谷上游延伸,因此失稳地区的滑坡数量也越来越多。 图9 30 mm 降雨研究区域坡度—比集水区面积图Fig.9 Slope-Contributing Area of study area in 30 mm rainfall 图10 50 mm 降雨研究区域坡度—比集水区面积图Fig.10 Slope-Contributing Area of study area in 50 mm rainfall 图11 100 mm 降雨研究区域坡度—比集水区面积图Fig.11 Slope-Contributing Area of study area in 100 mm rainfall 图12 200 mm 降雨研究区域坡度—比集水区面积图Fig.12 Slope-Contributing Area of study area in 200 mm rainfall 为了得到研究区内降雨触发滑坡的阈值,绘制不同降雨量与滑坡总面积中失稳分区所占滑坡面积变化曲线如图13所示。 图13 失稳分区中滑坡面积占滑坡总面积的比例统计曲线Fig.13 Statistical curve of the proportion of the landslide area in the total landslide area in the instability zone 由图13 可知,滑坡总量的50%触发于日降雨量小于50 mm 的工况下。分布在失稳分区中的滑坡比例,随降雨强度的加强呈线性增长。当日降雨量为100 mm时,位于失稳分区中的滑坡占比高达62%。由此可认为当日降雨量大于100 mm 时,大部分的滑坡可能处于变形失稳的状态,即触发柳林县滑坡危险性的降雨阈值约为100 mm/d。 基于SINMAP 模型评价结果发现,日降雨量为100 mm 时,研究区总面积的63%分布于潜在不稳定区、不稳定区以及极不稳定区。滑坡总数的61.9%分布于预测的不稳定区,共计39 个滑坡点,其中潜在不稳定区分布了38 个滑坡。以上分析结果说明SINMAP 模型对模拟不同降雨条件下区域斜坡的稳定性的预测具有有效性。 为了进一步验证SINMAP 模型对研究区的预测具有有效性,选取了研究区内3 个典型滑坡与模拟结果进行对比。3 个典型滑坡分别为贺家坡村西滑坡,聚财塔村滑坡和苇园沟村滑坡,地貌上均属于黄土梁峁侵蚀堆积区,地形切割强烈。出露地层为第四系中上更新统粉质黏土及粉土,在降雨的诱发下,表层土体沿下伏地层层面发生滑动,形成滑坡。将典型滑坡点与模拟得到的地表稳定指数分布图进行对比,其对比结果如图14所示,由图14 可知该模型在降雨条件下对研究区的已有滑坡预测准确,可应用于黄土地区的区域斜坡稳定性预测。 图14 分布示意图Fig.14 Schematic diagram of distribution 通过SINMAP 模型在柳林县范围模拟得出的预测结果与现有的滑坡灾害分布对比分析可知,模型在黄土地区的应用具有适用性,但模拟结果与实际还是有一定的差距,考虑到模型在输出精度上不仅受数字高程模型影响较大,而且受到已知滑坡精确定位的影响。如果DEM 分辨率越高,已知滑坡定位越精确,则模型计算结果越准确。 (1)应用SINMAP 模型,对柳林县不同降雨量下的滑坡变形失稳的可能性,进行了模拟预测。研究发现,随着降雨量的增加,区域内饱和程度增加,处于稳定状态的地区逐渐减少,与此相反,处于失稳状态的地区逐渐扩张,说明降雨对该研究区的斜坡稳定性影响较为明显。 (2)当日降雨量超过100 mm 时,失稳分区中滑坡比例超过63%,表明触发柳林县滑坡失稳的降雨量阈值大约为100 mm/d。 (3)应用SINMAP 模型,分析探讨了随着研究区内降雨量的增加,滑坡变形失稳区域的空间分布变化情况。研究表明,随着降雨量的增加,滑坡所处位置逐渐由稳定状态向失稳状态发展,位于失稳分区的滑坡数量逐渐增加。通过将模拟结果与实际由降雨触发的滑坡灾害进行对比分析,发现SINMAP 模型在黄土地区模型预测结果与实际浅层滑坡空间分布具有一致性,证实SINMAP 模型对区域性降雨诱发浅层黄土滑坡稳定性的模拟预测有效,可以用于黄土地区浅层滑坡的稳定性评价研究,对该地区的土地规划和减灾防灾具有一定的参考价值。

2.2 数据来源
2.3 参数设置

2.4 稳定性指数

3 不同降雨条件下滑坡变形失稳预测




4 滑坡变形失稳预测结果及误差验证
4.1 滑坡变形失稳预测结果验证
4.2 误差分析
5 结论和建议
——以连云港市为例

