C 波段双偏振雷达降水估计的误差分析与建模*
唐佳琪 寇蕾蕾,2 蒋银丰 楚志刚 陈爱军,2
1.南京信息工程大学大气物理学院,南京,210044
2.南京信息工程大学气象灾害预警与评估协同创新中心,南京,210044
1 引言
降水与水文、农业畜牧业生产及其他科学和社会应用息息相关,但是要得到高精度降水产品存在很大的挑战。地面雨量站观测可以准确获取雨量计所在位置的降水量,但是基于地面雨量站观测的降水插值产品精度严重受到地面雨量站点的疏密和空间分布影响。双偏振雷达可提供比常规多普勒天气雷达更多的回波信息(差分反射率ZDR、差分传播相移 ΦDP和差分传播相移率KDP),利用这些偏振参量可以获取水凝物的相态、空间取向、降水类型等信息,从而可提高降水强度的估测精度(寇蕾蕾 等,2018;黄 兴 友 等,2019;Zhao,et al,2019;Wijayarathne,et al,2020;Voormansik,et al,2020;张哲,2021)。目前中国很多省份已将天气业务雷达升级为双偏振雷达,在这种发展趋势下,提高双偏振雷达测量降水精度尤为重要。
双偏振雷达数据质量控制以及误差分析对雷达数据的应用十分重要。杜牧云等(2013)、胡志群等(2008)和黄兴友等(2019)对双偏振雷达不同衰减订正方法做了对比,提出使用综合法衰减订正效果更好,即在不同阈值范围上分别用KDP和ZH拟合衰减系数并进行衰减订正;刘黎平等(2007)、寇蕾蕾等(2018)基于雨滴谱和雨量计资料分析了双偏振雷达测量数据性能和定量估测降水的精度情况,发现使用偏振参量能明显提高降雨估测精度并分析了信噪比对雷达数据质量的影响。国际上许多专家学者基于双偏振雷达定量降水估计的研究工作也取得了不少成果(Park,et al,2017;Thompson,et al,2018;Voormansik,et al,2020;Wijayarathne,et al,2020)。雷达降水估计误差的来源有很多方面,Villarini 等(2010)从雷达校准误差、衰减、地物杂波和波束异常传播、波束阻塞、Z-R关系的可变性、距离退化效应、降水系统的垂直变率、大气垂直运动和降水系统漂移以及时间采样误差等方面总结了天气雷达估测降水误差的来源。Seo(2010)通过参数化雷达反射率非均匀垂向剖面结构,推导出雷达降水估算中与距离相关的误差(RED)统计模型。Berenguer 等(2009)建立了随机时空模型来量化雷达采样误差,估计了雷达降雨累计过程中采样误差的分布,包括时间空间采样误差、反射率垂直剖面采样误差以及Z-R不确定性所造成的误差。但在实际应用中,很难对每一个误差来源进行建模和分析,因此寻找总误差的误差模型相对更加方便。对于雷达探测总误差的分析,Kirstetter 等(2010)通过对雷达估计值与雨量计雨量之间的残差分布进行分析,发现其残差分布是对称的,可以用高斯模型近似描述,甚至可以用双指数模型更好地描述。AghaKouchak 等(2010)建立的模型将雷达误差分为纯随机误差和与雨强大小成正比的误差分量,该模型在生成具有与无扰动雷达估计相似的随机特征和相关结构的雷达降雨场集合方面表现良好。对于空间采样误差,Wang 等(2010)和Bringi等(2011)通过对雷达误差方差分离的方法,分析了空间尺度不匹配问题造成的雷达误差,结果表明空间不匹配造成的误差在总误差中的占比很大,且随雨强阈值的增大而增大。Ciach 等(2007)将雷达估计降水的误差建立乘法模型,得到确定性偏差函数+随机噪声的误差模型。值得注意的是,在利用雨量计资料对雷达定量降雨估测误差进行分析时,会存在时间采样误差和空间尺度不匹配的问题。
本研究利用南京信息工程大学C 波段双偏振多普勒天气雷达的探测资料,分析该雷达定量降水估 计(Quantitative precipitation estimation,QPE)不同降水反演公式的性能及误差分布,并对总误差进行雨量计代表性误差分离以及误差量化建模。首先对双偏振雷达的数据进行预处理,包括衰减订正和 ΦDP滤波、KDP计算以及有效数据筛选。然后基于南京信息工程大学观测基地的雨滴谱仪数据,利用T 矩阵法计算双偏振参数ZH、ZDR、KDP,拟合测雨方程,并将R(ZH)、R(ZH,ZDR)、R(KDP)、R(KDP,ZDR)4 个测雨公式的计算结果与2015—2016 年的雨量计数据进行对比,分析双偏振雷达测雨性能。基于雨量计之间的距离和其数据相关关系,计算由于空间不匹配造成的雨量计代表性误差,并将雨量计代表性误差从雷达总误差中分离,得到雷达降水估计误差,讨论分析雷达测量误差和参数误差占总误差的比重以及4 个测雨公式的性能;将雷达误差按照系统误差和随机误差进行误差量化建模,分析误差分布规律。最后,根据对4 个测雨公式的误差和性能分析,提出一个优化的双偏振雷达组合降水反演算法。
2 数据介绍及预处理
2.1 数据介绍
使用的雷达探测数据来源于南京信息工程大学C 波段双线偏振多普勒天气雷达(简称NUISTCDP 雷达)。该雷达位于南京信息工程大学气象楼楼顶,站点坐标为(32°12′N,118°43′E),2014 年安装完成并投入使用。雷达天线直径8.5 m,扫描半径150 km,脉冲宽度为0.5 µs,距离库长为75 m,波束宽度为0.54°。该雷达完成一次体扫需要7—8 min,可探测得到水平反射率因子(ZH)、径向速度(V)、速度谱宽(W)、差分反射率因子(ZDR)、差分传播相移(ΦDP)、差分传播相移率(KDP)、0 滞后相关系数ρHV(0)等双偏振参量。
为了检测双偏振雷达的衰减订正效果,将与南京龙王山S 波段雷达(简称SA 雷达)对比。SA 雷达与NUIST-CDP 雷达相距2.5 km 左右,雷达高度相差50 m 左右,距离比较接近。C 波段雷达每次体扫时间为7—8 min,而SA 雷达6 min 完成一次体扫,因此可选取两雷达开始体扫时间较近的数据进行对比。
雨滴谱资料来源于一台OTT Parsivel 雨滴谱仪,该雨滴谱仪安装在南京信息工程大学大气综合观测基地,站点坐标为(32°12′N,118°42′E),仪器位于较平坦且空旷的地面,因此受地物影响较小。该雨滴谱仪距NUIST-CDP 雷达约1800 m,相对雷达的方位角约为250°。该资料将在计算C 波段双偏振雷达衰减系数和反演雷达公式时使用。
在与雷达反演结果对比、雷达误差分析时都将雨量计测量值作为近似真值。使用2015—2016 年江苏省南京市各站点的雨量计数据,位于雷达范围内的地面雨量计共有539 个,分布如图1,其中雷达位于坐标原点。图中五角星表示在一个雷达像素内包含两个雨量计,这4 个像素将在接下来雨量计点面误差分析时使用。
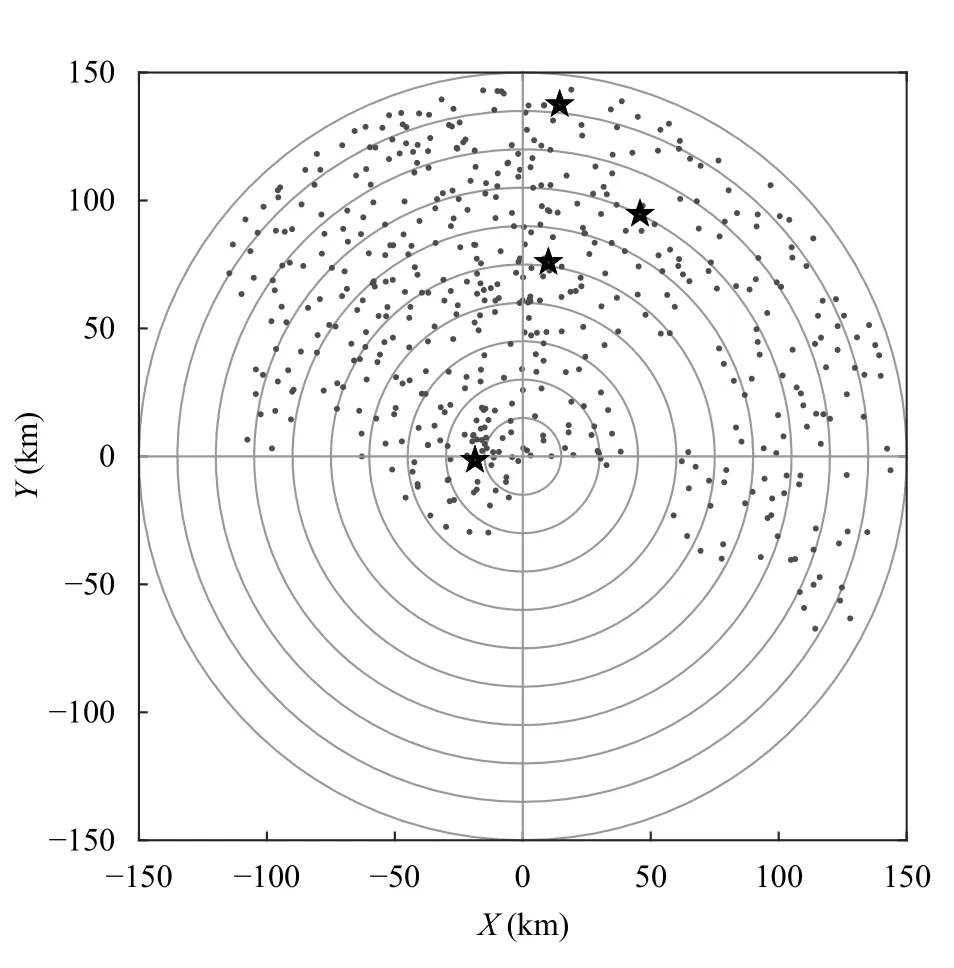
图1 雨量计与雷达空间分布Fig.1 Map of rain gauge and radar spatial distribution
2.2 双偏振雷达数据预处理
双偏振雷达资料易受环境噪声和衰减等因素的影响而抑制双偏振雷达参量的应用效果,因此在使用双偏振雷达数据前需对数据进行预处理。预处理主要步骤如下:
(1)对ΦDP进行中值滤波,去除异常值,使数据变得平滑。因为ΦDP异常出现往往是连续的,较小的滤波数难以平滑ΦDP的异常点,所以采用40 点中值滤波。
(2)利用ΦDP计算KDP,文中采用最小二乘法计算KDP,对40 个距离库区间进行最小二乘法拟合。KDP计算公式为
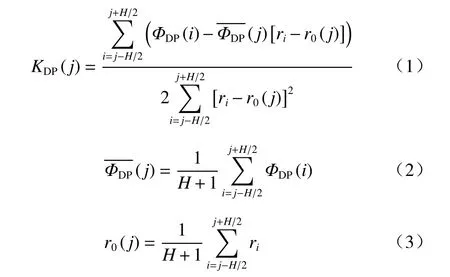
式中,H是最小二乘法距离库区间个数,文中对40 个距离库区间进行最小二乘拟合,即H=40,是所求点前后各H/2个距离库共H+1 个距离库的平均值,r0是这H+1 个距离库与雷达的平均距离。
(3)对雷达反射率因子(ZH)和差分反射率因子(ZDR)进行衰减订正。胡志群等(2008)、黄兴友等(2019)等发现,在实际的雷达观测中,KDP具有独立于雷达系统标定、受滴谱分布变化小、没有雨区衰减效应和波束传播阻挡效应等优势,可以运用于雷达回波强度的衰减订正。但当KDP<0.1°/km 时,KDP的值较小,易受雷达自身噪声以及其他因素的影响,可靠性不高,可用ZH来订正。ZH衰减订正具体方法为:在0.1≤KDP≤3°/km 时,衰减率AH用AH=a1×KDP计算;在KDP<0.1°/km 及KDP>3°/km 时文中利用2015—2016 年的雨滴谱数据,通过T 矩阵方法计算得到偏振参数,并通过拟合得到参数值,其中a1=0.08648 dB/°,a2=1.07×10−5dB/km,b2=0.8963。ZDR的衰减率ADP参数拟合方法与AH类似,在此不再赘述。
(4)有效数据筛选。由于雷达数据容易受到雷达附近地物杂波及雷达噪声等因素影响,使得雷达近处偏振量很不稳定,所以在降水反演时剔除了20 km 以内的数据。寇蕾蕾 等(2018)、陈超 等(2018)通过对信噪比(SNR)数据的分析,发现当信噪比小于20 dB 时,ZDR不是很稳定,KDP数据在近距离和弱回波区域质量不是很好,为了更好地比较各测雨公式的测雨效果,降水反演时剔除了信噪比小于20 dB 的数据,同时也剔除了ZH、ZDR、KDP小于0 的站点数据。
为了说明ZH衰减订正效果,图2a 和b 分别为NUIST-CDP 雷达和SA 雷达0.5°仰角的原始反射率因子PPI,图2c 显示了NUIST-CDP 雷达反射率因子经过衰减订正后的PPI,其中NUIST-CDP 的体扫起始时间为2015 年6 月27 日00 时32 分(世界时,下同),SA 雷达体扫时间为2015 年6 月27 日00 时31 分,这天南京出现了持续大雨,部分地区出现暴雨甚至大暴雨。图像显示范围均在距离雷达150 km 以内,两雷达回波形状相似,但因为C 波段雷达采用0.5°方位分辨率和75 m 径向分辨率,所以回波结构更清晰。NUIST-CDP 的回波强度明显偏低,经过衰减订正后的图2c 可以看到C 波段双偏振雷达的数据有所修正,但和S 波段雷达回波比还是存在误差,也说明对C波段双偏振雷达订正的必要性。为更好地进行定量对比,需使NUIST-CDP 与SA 雷达空间分辨率基本一致,因此量化对比时将NUIST-CDP 数据进行了13 或14 个距离库的平均,使径向分辨率变为1 km,方位上进行了最近邻点插值,使方位分辨率变为0.5°左右。图2d 是两部雷达时空匹配后的反射率因子散点。NUIST-CDP 回波观测值整体弱于SA 雷达,平均偏差(SA−CDP)达6.4623 dB,经过衰减订正后,平均偏差减小为3.68684 dB,可以看出衰减订正对ZH有一定的校正作用。
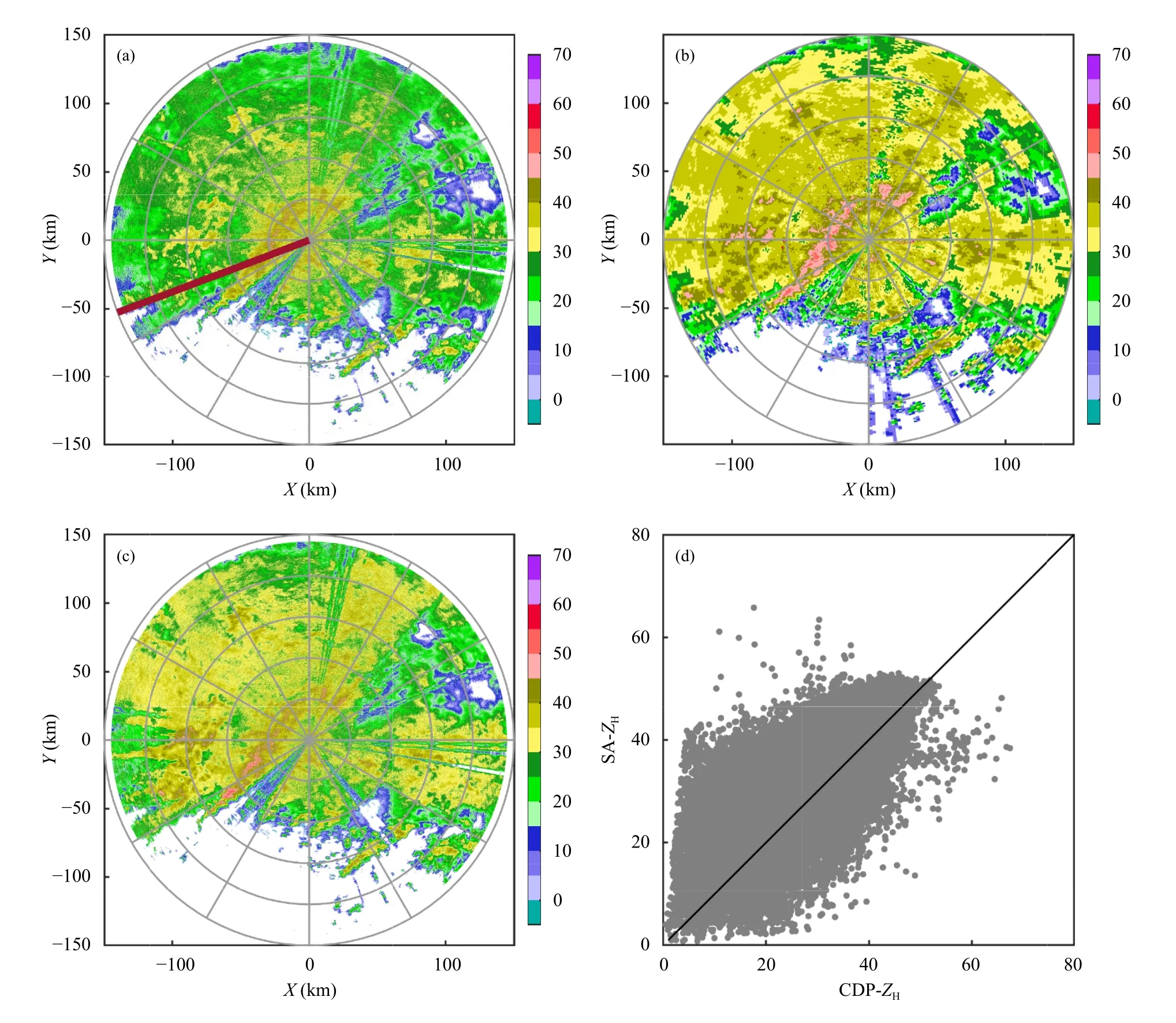
图2 2015 年6 月27 日00 时32 分0.5°仰角 ZH(单位:dBz)数据PPI(a.C 波段雷达原始 ZH,b.SA 雷达原始 ZH,c.C 波段雷达衰减订正后的 ZH,d.NUIST-CDP 雷达和SA 雷达 ZH的散点)Fig.2 PPI images of(a)original ZH of NUIST-CDP,(b)original ZH of SA radar,(c)ZH of NUIST-CDP after attenuation correction at 0.5° elevation at 00:32 UTC 27 June 2015 and(d)scatter plot of ZH from NUIST-CDP and SA randar(unit:dBz)
为了更好说明数据预处理的效果,图3 给出了图2a 中红色径向上数据预处理前、后对比。图3a是ΦDP数据中值滤波前、后的距离廓线对比,从图中可以看出,离雷达较近的约200 个距离库(15 km)的ΦDP数据质量很差,波动较厉害,这可能主要受地物杂波的影响,数据不可用,需要剔除。在200 个距离库之后,ΦDP随着距离库数的增加而增大,趋势明显且连续性很好,中值滤波使得数据变得平滑,消除了原始数据中的一些小的高频噪声。图3b 为KDP数据经过最小二乘法处理前后的对比。通过比较可以看出,利用最小二乘法计算得到的KDP数据与原始数据一致性较好,且在原始数据出现异常的地方,用最小二乘法计算得到的数据保持了正常,说明对ΦDP滤波的有效性。图3c 是ZH衰减订正前、后以及SA 雷达ZH的对比,通过观察发现,降水的ΦDP最大在150°左右,而杂波的ΦDP普遍较大,因此在使用KDP订正ZH时需剔除ΦDP大于150°的值,在此径向上显示为1500 个距离库(112 km)之后的数据,因此此图上只显示了112 km 以内的数据。从图中可以看出,在110 km 左右,路径衰减约为10 dB,差分传播相移约为140°。且通过与SA 雷达的ZH数据对比可以看出,衰减订正的效果较好,ZH经过衰减后的数据基本与SA 的结果差距较小。图3d 是经过衰减订正的ZDR的 对比,在110 km 处,路径差分衰减接近3 dB。经过雷达数据预处理后,接下来将利用预处理后的雷达数据进行降水估计以及降水误差分析。
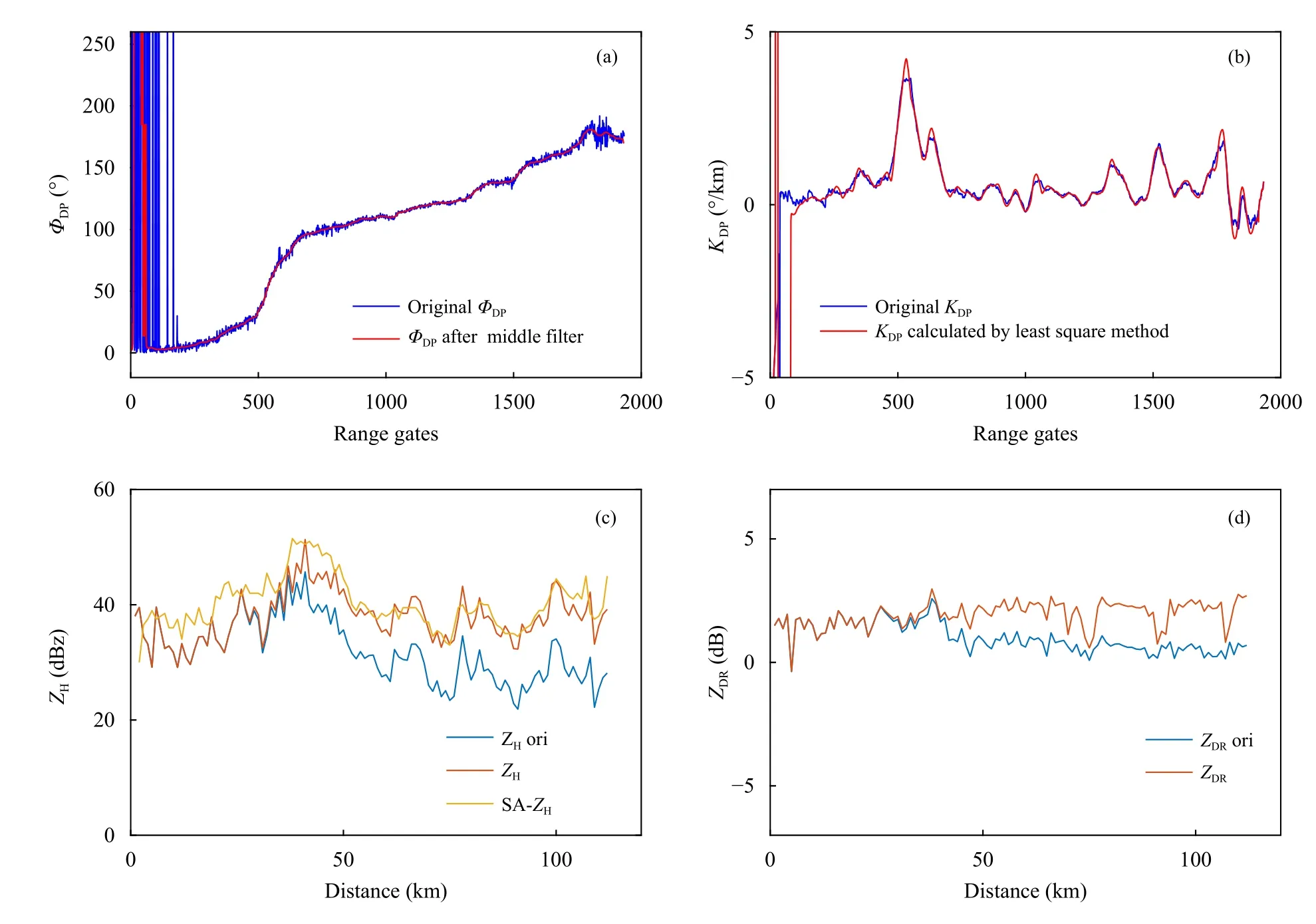
图3 NUIST-CDP 雷达249°方位角上距离廓线对比(a.ΦDP,b.KDP,c.ZH,d.ZDR;图c 黄色线为对应S 波段廓线数据)Fig.3 Distance profile comparison of ΦDP (a),KDP (b),ZH (c) and ZDR (d)data before and after processing at 249°azimuth angle from NUIST-CDP(the yellow line in c is the corresponding S-band profile data)
3 双偏振雷达降水估计误差分析
在对雷达数据进行误差分析时,使用雨量计数据作为近似地面真实降雨量和雷达反演降水数据进行对比。首先基于南京信息工程大学雨滴谱资料计算偏振参数,拟合适合南京地区降水特征的雷达降水方程;其次,利用南京市雨量计数据作为近似真值,与雷达降水反演结果对比,统计分析雷达公式在不同雨强阈值的反演性能;随后,分析由于雨量计和雷达数据空间不匹配造成的误差对雷达误差的影响,并分析雷达测量误差和参数误差占雷达降水估计误差的比重;最后将雷达降水估计误差分为系统误差和随机误差并建立误差模型。
3.1 雷达降水估计公式拟合
雷达降水估计公式拟合时所用的雨滴谱数据为2015—2018 年夏季南京信息工程大学探测基地雨滴谱仪收集到的每隔10 s 一次的采样数据,拟合前对原始采样数据进行了1 min 中值滤波,以消除数据的脉动。基于这些滴谱数据计算ZH、ZDR、KDP等偏振参量,然后用雨滴谱仪输出的降水强度,采用一元非线性回归和多元非线性回归法进行了雷达测雨公式的拟合。图4 为4 个测雨公式的拟合效果,横坐标为雨滴谱仪测得的雨量值,纵坐标为各测雨公式计算得到的雨量值。表1 是各测雨公式拟合系数和拟合结果的相关系数。从图4 和表1 可以看出,在加入了KDP的测雨公式中,拟合的相关系数较高,说明了KDP测量降水的优越性。因为KDP与降水粒子直径的3 次方成正比,ZH与降水粒子直径的6 次方成正比,而降水量大致与降水粒子的3 次方成正比,这就意味着KDP与降水量成线性关系,用KDP来测量降水受雨滴谱型变化很小,而ZH相对于KDP和ZDR来说对雨滴谱敏感性较大,受粒子直径影响较大,因此用ZH拟合的结果在4 个公式中略差。

表1 测雨公式拟合结果Table 1 Fitting results of rain measurement formula
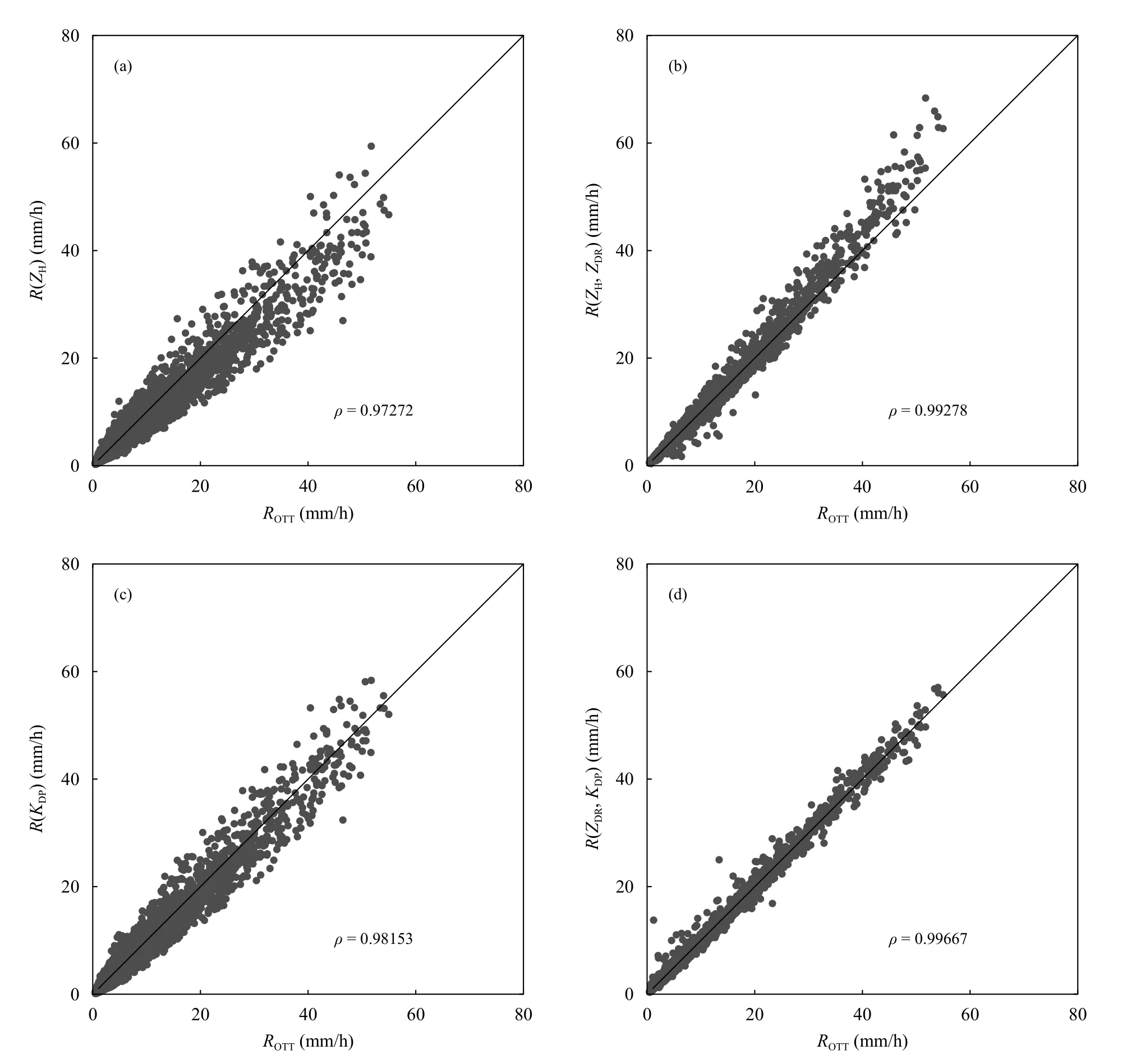
图4 测雨公式拟合结果与观测值散点(a.R1=,b.R2=,c.R3=,d.R4=)Fig.4 Scatter plots of fitting results of radar rainfall formula and observed values from raindrop spectrograph(a.R1=,b.R2=,c.R3=,d.R4=)
3.2 雷达降水估计与雨量计数据对比
为验证NUIST-CDP 雷达定量降水估计的效果,以南京市雨量站测量值为基准与雷达估测数据进行对比。由于雨量计数据为1 h 降水量,而雷达在1 h 内平均有8 次体扫数据,为了将雷达数据与雨量计数据进行时间匹配,将雷达数据进行1 h 平均,从而比较每个雨量计位置上基于雷达的逐时降雨累积量。文中所使用的雷达数据均为0.5°仰角数据。NUIST-CDP 雷达的像素为0.5°×75 m,因为ZDR、KDP数据起伏波动较大,为提高数据稳定性,选取1°×225 m 面积上的雷达数据平均值与雨量计数据做比较,即离雨量计所在位置最近两方位角上各3 个雷达像素的降雨率进行平均,并且每个雷达像素上的值具有相同的权重。
图5a—d 分别表示表1 中4 个降水公式估测值和雨量计测量值的对比散点,其中横坐标代表雨量计值,纵坐标表示双偏振雷达测雨公式反演降雨量值。图5a 是原始ZH数据和经过衰减订正的ZH数据通过R(ZH)公式计算得到的值与雨量计的对比。从图5a 中可以看出,经过衰减订正的ZH数据反演效果比原始ZH数据效果好,再次说明C 波段双偏振雷达衰减校正的重要性。R(ZH)和R(ZH,ZDR)降水反演结果在雨量较大时明显小于雨量计雨量值,这可能主要是由于C 波段雷达的ZH、ZDR在传播过程中衰减造成的。R(ZH)的计算结果在比较低的阈值内相关较好,R(KDP)在较高的阈值时,相关显著增强。
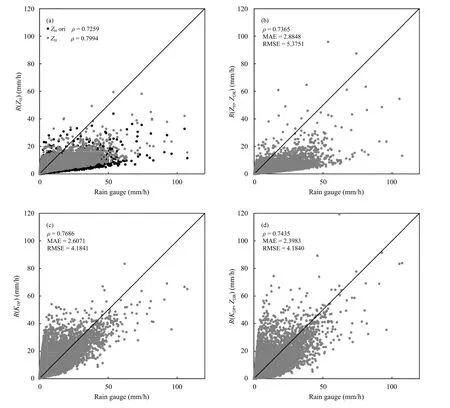
图5 NUIST-CDP 雷达降水强度与地面雨量计对比(a.R(ZH),b.R(ZH,ZDR),c.R(KDP),d.R(KDP,ZDR))Fig.5 Comparison of the NUIST-CDP radar calculated precipitation intensity and the ground rain gauge(a.R(ZH)method,b.R(ZH,ZDR)method,c.R(KDP)method,d.R(KDP,ZDR)method)
下面将基于4 个测雨公式及R(ZH原)(原始ZH数据计算的降水强度),分析各测雨公式的降水估计性能。表2 显示了每小时降雨阈值大于0.2、1.0、
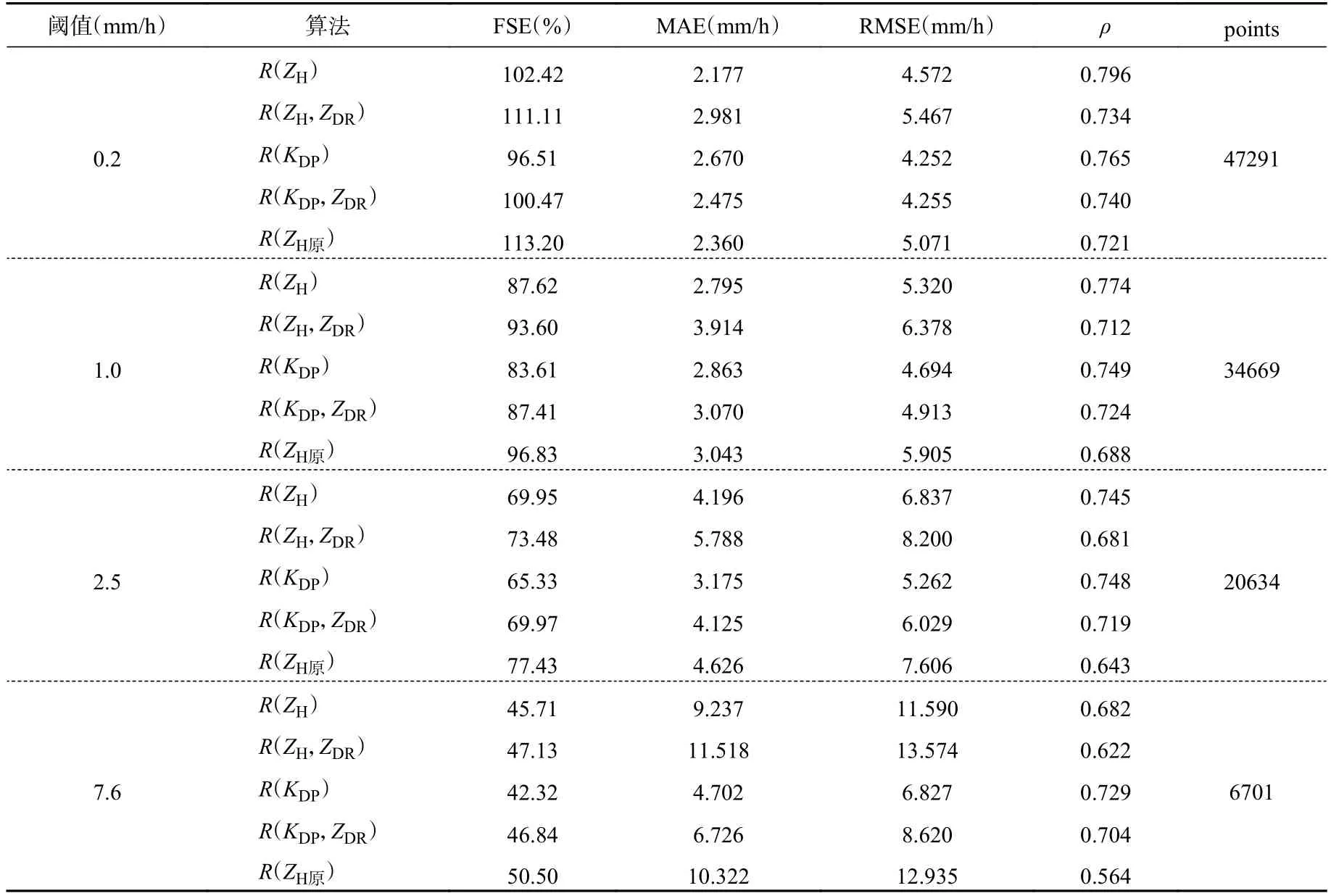
表2 不同阈值下各测雨公式统计性能分析和统计使用的样本数Table 2 Key statistics of radar-gauge comparison for four thresholds along with the number of samples used in computing the statistics
2.5 和7.6 mm 时雷达和雨量计对比的一些统计数据结果,以及用于计算的数据样本数(张贵付(2018)中,将降水强度分为小雨(<2.5 mm/h),中雨(2.5—7.6 mm/h),大雨(>7.6 mm/h))。该表显示了分数标准误差(FSE,以%为单位)、皮尔逊相关系数(ρ)、均方根误差(RMSE)和平均绝对误差(MAE)的统计结果,这些参数定义如下
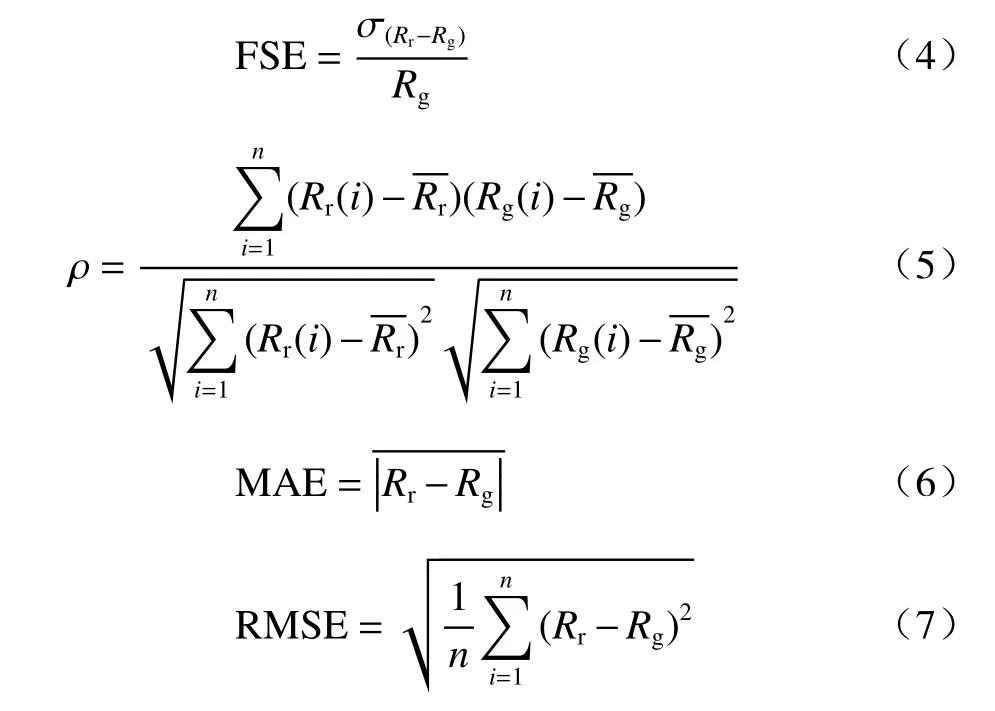
式中,σ为Rr−Rg的标准偏差,单位mm/h;Rr为雷达估计降水量;Rg为雨量计测量降水量;FSE 是雷达和雨量计误差的归一化标准差,值越小误差越小;相关系数表示雷达和雨量计数据的相关程度,越接近1 相关性越高;MAE 是雷达雨量计的误差绝对值的平均值,值越小实际误差越小;RMSE 是观测值同真值之间的偏差,值越小表明测量值与观测值的偏差越小。一般情况下,阈值越高,FSE 越低。
FSE 是雷达估测降雨强度和雨量计总误差的归一化标准差,反映雷达总误差的离散程度,总体来看R(KDP)的FSE 在4 个公式中最小,说明R(KDP)的总误差分布较为集中,误差总和较小;且对于每一个单独的测雨公式,FSE 随着阈值的增大而减小,符合预期。MAE 反映绝对偏差的平均值,在小雨时R(ZH)的偏差最小,随着阈值的增大,到达中雨以后R(KDP)偏差较小。RMSE 反映了误差观测值与测量值的偏差,可以看出在任何降雨阈值范围内含有KDP公式计算得到的值与雨量计的偏差较小。相关系数反映雷达和雨量计数据的相关程度,在降雨阈值为0.2 mm/h 时,用ZH计算的降雨强度相关较强,在0.79 左右,但随着降雨阈值的增大R(ZH)的相关系数降到0.68,说明ZH在小雨时候的测量值更准确。R(KDP)的结果与R(ZH)结果正好相反,在降雨阈值较小的时候相关系数比R(ZH)低,但当阈值大于2.5 mm/h 时,其相关在4 个测雨公式中最高。综合所有统计结果,R(ZH)在弱降水时效果最好,当降雨阈值大于2.5 mm/h 时,R(KDP)的优势得以突显。通过R(ZH)和R(ZH原)的对比,R(ZH原)的结果都比R(ZH)差,也说明了在应用Z-R关系之前校正降雨衰减的重要性。在加入了ZDR后的测雨公式效果与只含有ZH、KDP的测雨公式变化趋势一致,但并没有优于原测雨公式,这可能是受到雷达ZDR数据质量(本身系统误差)及衰减订正效果的影响。
3.3 雷达降水估计误差分析
3.3.1 雷达降水估计与雨量计数据空间误差分离
许多研究人员已经认识到,雷达估测雨量和雨量计雨量的差异不能被直接视为雷达降水估计误差,部分误差应归因于雨量计提供的是点测量值,而雷达降水估计代表了一个区域的值。这种由于雨量计和雷达的测量空间尺度不匹配造成的误差,可以称为雨量计代表性误差(gauge representativeness error)。雨量计代表性误差是由Kitchen 等(1992)提出并由Ciach 等(1999)进一步发展。其基本思想是将雷达估测雨量和雨量计雨量的差分为两项:雨量计代表性误差和雷达降雨估计误差。因此雷达估测雨量和雨量计雨量的误差方差可以表示为

式中,var 和cov 分别表示随机变量的方差和协方差,Ra为真实地面平均降雨量,Rr为由雷达参量计算得到的降雨量,Rg为雷达像素内雨量计测得的降雨量。假设雷达和地面真实降水量的偏差与雨量计和地面真实降水量的偏差不相关,协方差项就可以忽略。因此,通过对式(9)的整合,可以得到雷达降雨估测误差方差为
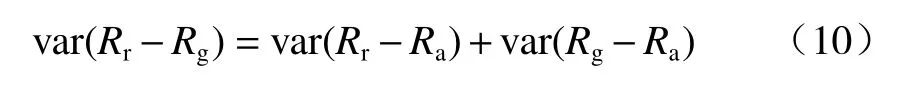
式(10)右边第一项为雷达估测雨量和雨量计雨量的总误差方差;右边第二项为雨量计代表性误差方差,是由于空间尺度不匹配造成的误差,称为点面误差方差,可以表示为
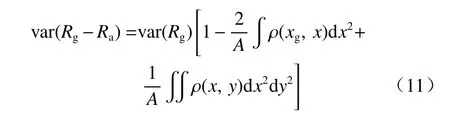
式中,var(Rg)是雨量计测量方差,A为雷达像素在(x,y)坐标的面积域,ρ(x,y)是空间相关函数,xg是仪表在雷达像素内的位置。
利用皮尔逊相关系数计算相关函数,并假设空间相关是各向同性的。为了表示空间相关函数,使用了三参数指数模型(Habib,et al,2002)
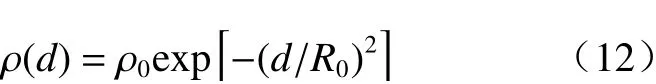
式中,d表示任意两雨量计之间的距离,R0是相关距离,F是形状参数,ρ0是熔核参数。根据Krajewski等(2003),ρ0表示由于微尺度变化或随机仪器误差而引起的去相关,其范围为0.95—0.97。F用来形容拟合结果的线条形状,R0表示在这个距离之外,两点间区域变量的样本值的相关可忽略不计。
使用2015—2016 年夏季的雨量计数据,利用莱文贝格-马夸特方法(Levenberg-Marquardt 算法,简称LMA,一种非线性最小二乘算法)对雨量计数据进行非线性最小二乘法拟合,结果如图6 所示。图6a—c 分别表示当雨量计阈值大于0、0.2 和1.0 mm/h 时的相关函数。从图6 可以看出,雨量计数据相关随着距离的增大而减小,且更高的阈值存在更强的分散。
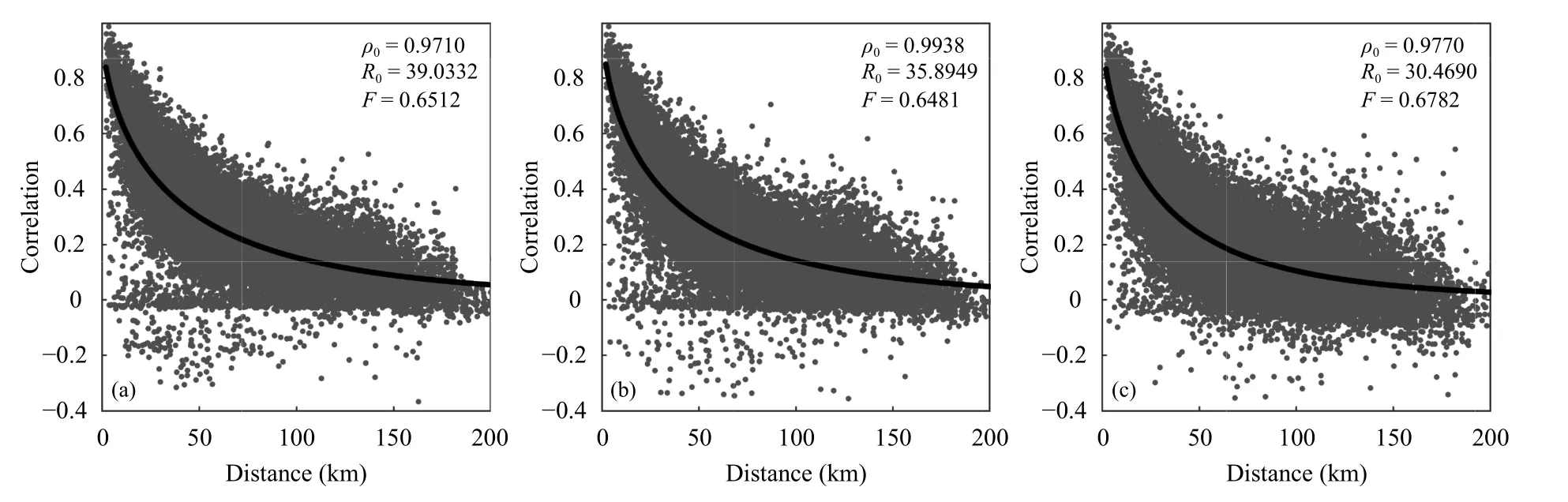
图6 不同降雨阈值下的空间相关函数(降雨阈值大于(a)0、(b)0.2、(c)1.0 mm/h)Fig.6 Spatial correlation functions for different rainfall thresholds using 60-min accumulations(The rainfall threshold is greater than(a)0,(b)0.2,and(c)1.0 mm/h )
图7a 显示了存在多个雨量计的雷达像素内的雨量计雨量与真实地面平均降雨量的60 min 累计对比散点。因为雨量计的分布比较分散,文中使用的雷达像素较小(面积0.01—0.57 km2不等),经过筛选有两个雨量计的雷达像素区域有4 个,即图1 中五角星所在位置。这几个像素区域的平均面积为0.3326 km2。如图7a 所示,即使在这么小的区域内,雨量计测量的降水量和像素平均降水量也会有很大差异。图7b显示了点面误差方差var(Rg−Ra)随Ra的变化趋势,可见var(Rg−Ra)趋于随平均降雨量的增大而增大。
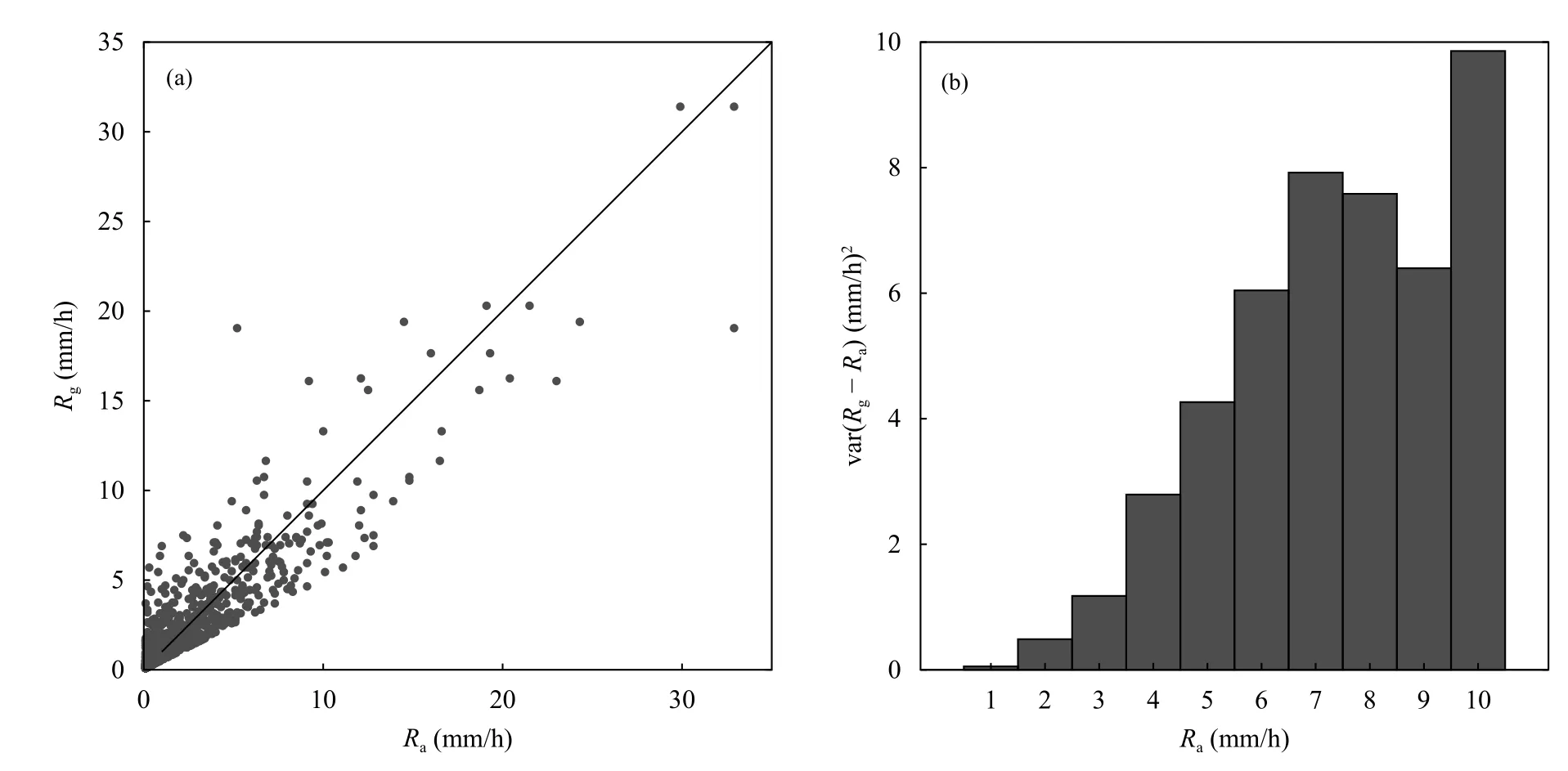
图7 (a)雨量计降水量与区域平均降水量散点,(b)var(Rg−Ra)随平均雨强的变化趋势Fig.7 (a)Scatterplot between the true area-averaged rainfall Ra vs point gauge Rg rainfall and(b)gauge representativeness error var(Rg−Ra)vs mean areal rainfall Ra
图8a 是点面误差方差与雷达雨量计总误差方差的比例。含有ZH的公式受点面误差影响较小,在雷达像素平均面积为0.33 km2的区域内,R(ZH)的点面误差方差占比从阈值0.2 mm/h 时的0.5%左右增长到阈值为7.6 mm/h 时的5%,而R(KDP)点面误差方差占总误差方差的比重增长较快,其点面误差方差所占比例从阈值0.2 mm/h 时的0.5%左右变化到阈值为7.6 mm/h 时的17%左右。由此可见,点面误差是雷达和雨量计误差的重要组成部分,且随着阈值的增大而增大。因此,在平滑数据、降低分辨率时需要考虑点面误差对雷达定量降雨估计的影响。图8b 是4 个雷达测雨公式和R(ZH原)与雨量计总误差方差随降雨阈值的变化趋势。可以看出随着阈值的增大,所有测雨公式的误差方差都呈增长趋势,其中含有ZH的公式总误差方差增长较快,含有KDP的误差相对较小。总体来看,R(KDP)的方差相对较小,特别是在雨强阈值较大时,性能最好。另外,未经衰减订正的ZH计算结果的误差方差更大,也说明了衰减订正对双偏振雷达的重要性。
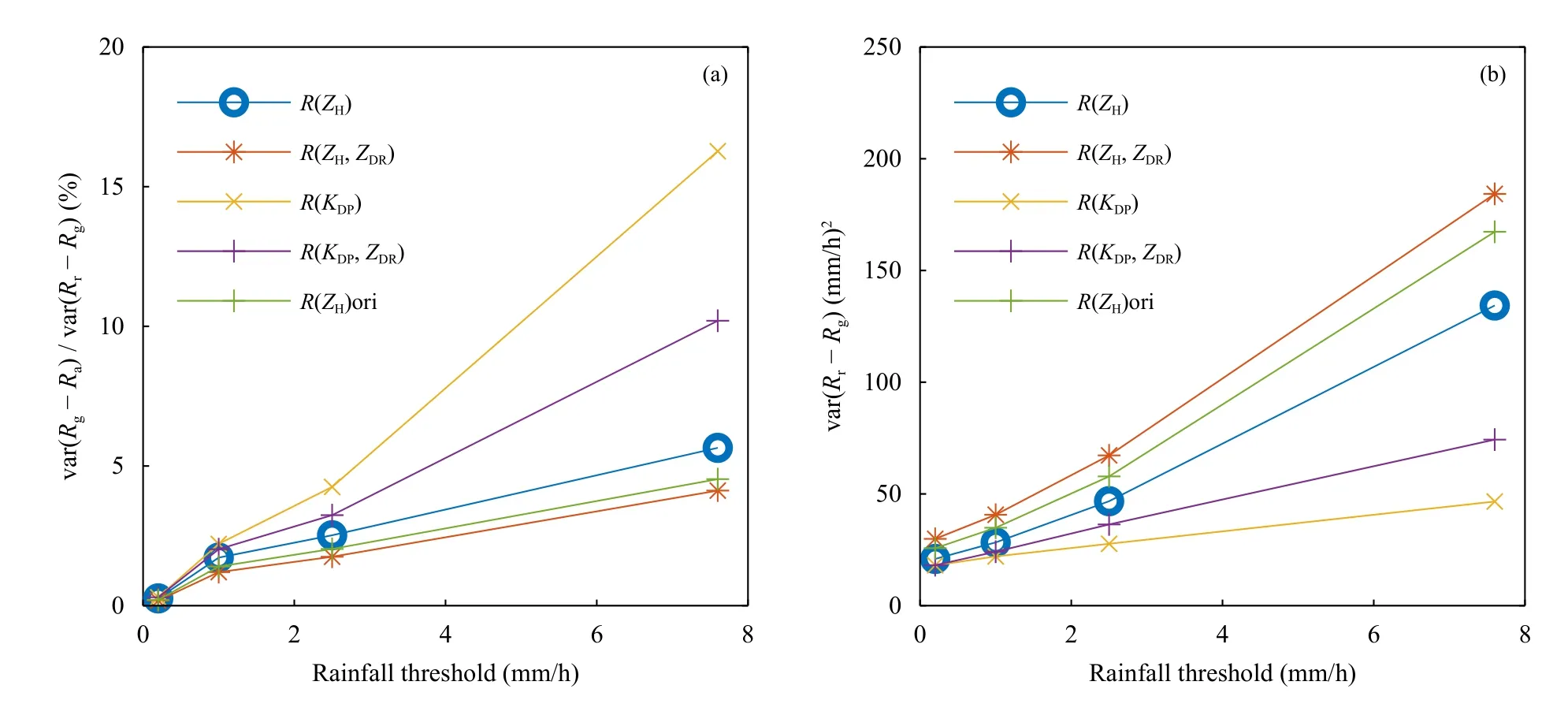
图8 (a)点面误差方差占雷达雨量计总误差方差的百分比,(b)各测雨公式的 var(Rr−Rg)随雨强的变化趋势Fig.8 (a)Ratio of point-to-area variance to the total error variance;(b)variance of(Rr−Rg)for the four algorithms used in the radar-based estimates,shown for various hourly thresholds of rainfall
3.3.2 雷达降水估计误差的分析
误差方差分离方法的核心是考虑雷达雨量和雨量计雨量的误差有多少是由雨量计代表性误差引起的,有多少是由其他雷达相关误差引起的,如参数化(或算法误差)、测量误差等。首先,将雷达雨量和雨量计雨量的误差分为点面误差(以下简称为var(p-to-a))和雷达降水估计误差,如式(13)所示。3.3.1节中分离了点面误差,雷达降水估计误差就可以表示为式(14),其中 ϵp是参数化(或算法)误差,ϵm是雷达测量误差,而 ϵ是随机(残余)误差。假定3 个误差的均值为0,并且进一步假定3 个误差均不相关。在此,将var(Rr−Ra)简称为雷达误差。
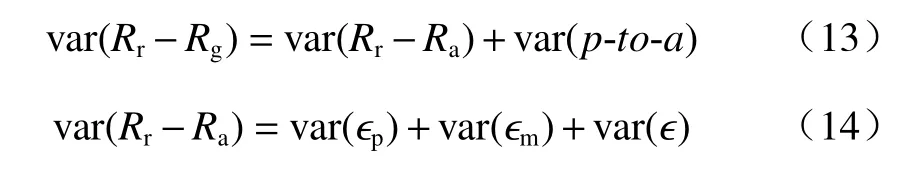
为了更好地分析雷达误差中各误差所占的比例,从式(10)中计算出雷达误差的标准偏差图9 以黑色实线显示了雷达误差的FSE=随降雨阈值的变化趋势。FSE 随降雨阈值的增大而下降,即类似从层状云降水到对流性降水的变化。图9 中的条形显示的是对算法误差和测量误差的FSE′的估计。下面以R(ZH)关系为例,简述参数误差 ϵp和测量误差 ϵm的算法(Bringi 等(2001))。已知R(ZH)的雷达公式为式(16),假设式(16)是无偏的Z-R算法,则σ2(ϵm)可表示为式(17),其中 σz是Z测量值的标准差。对于变化大的雨滴尺寸分布(或其他因子),一般无法得到它的测量误差,这时可以通过雨量计测量值和雷达估测值之差的方差来估计σ2(ϵp)。其他几个雷达测雨公式的σ2(ϵm)与R(ZH)同理。
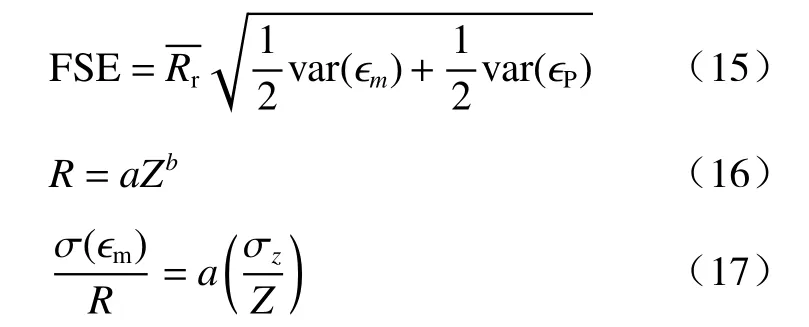
图9 是雷达测雨公式随阈值变化的误差趋势,其中实线为除去雨量计代表性误差后的误差,即为雷达降水估计误差。柱状图显示了雷达测量误差和参数误差所占比重,实线和柱状图中间的差异即为雷达的随机误差。可以看出,每个测雨公式的变化趋势基本一致,即测量误差和参数误差的归一化标准差随着阈值的增大而减小,随机误差随着阈值的增大而增大。且含有ZH的测雨公式误差更大,R(KDP)公式的误差相对最小。值得注意的是,式(15)中的因数为2 是由于两个波束的雷达数据是独立的,因此ZH、ZDR和KDP的测量误差将减少
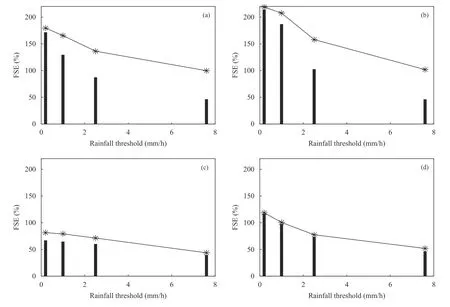
图9 四个测雨公式的雷达降水估计误差FSE 估计值(实线)(a.R(ZH),b.R(ZH,ZDP),c.R(KDP),d.R(KDP,ZDP);柱是式(15)的FSE′)Fig.9 Estimates of the FSE(solid line)for the radar precipitation estimation error for the four algorithms shown for various hourly thresholds of rainfall(a.R(ZH),b.R(ZH,ZDP),c.R(KDP),d.R(KDP,ZDP);bars represent FSE′ from Eq.(15))
3.3.3 雷达降水估计误差量化建模
分析误差属性及变化规律是未来发展降水算法优化、偏差调整技术、预报精度提升等研究的基础。雷达降水估计误差可建模为系统误差和随机误差,其中系统误差是由分析过程中一些固定的原因引起的,包括雷达反射率因子(ZH)等参数的测量误差、Z-R关系参数拟合造成的误差等,由于系统误差的存在,测量数据的平均值与真实值有较大的偏差。理想情况下,应该消除或最小化系统误差以减少整体不确定性。随机误差是雷达消除系统误差后仍然存在的误差,是不能用修正或采取某种技术措施的办法来消除的。不同来源的随机误差的叠加是雷达降水估计不确定的主要因素之一。将NUIST-CDP 雷达降水估计的误差建模为如下模型,如式(18)和(19),其中s为系统误差,ϵ为随机误差。a和b为线性回归拟合参数,分别称为回归系数和回归常数,用来解释系统误差。x表示真实雷达降雨量。

图10a1—d1显示了雷达定量估测降水的系统误差,可以发现,雷达近地面降水的系统误差和雨强成正比,且呈线性函数形式,总体趋势随着雨强的增大而增大。其斜率反映系统误差增长速度,斜率越大,误差随阈值增加越快,R(ZH)和R(ZH,ZDR)的斜率明显大于R(KDP)、R(KDP,ZDR),说明含有ZH的测雨公式系统误差随阈值的增大而迅速增大,在大雨时显示较大的误差。
图10a2—d2分别为4 个测雨公式随机误差概率分布和两种模型(高斯、双指数)拟合结果,其中纵坐标代表误差概率密度函数(PDF),横坐标表示误差值,mean 和standard 分别表示误差平均值和标准差。双指数模型定义为式(20),其中α为总体样本均值,β为总体标准差。高斯模型和双指数模型都通过总体的均值和标准差表示。通过对比分析可以发现,两种模型都可以反映随机误差的变化趋势,但双指数模型比高斯模型更贴合误差分布。消除系统误差后,随机误差的均值都接近于0。R(ZH)公式的随机误差为0 的概率约为0.39,而R(KDP)为0.25 左右,说明含有ZH的测雨公式随机误差分布更为集中。R(ZH,ZDR)和R(ZH)的随机误差分布类似,但R(ZH,ZDR)的随机误差更小;R(KDP,ZDR)的随机误差为0 的概率密度比R(KDP)随机误差为0 的概率密度更集中,都说明含有ZDR的公式随机误差更小。
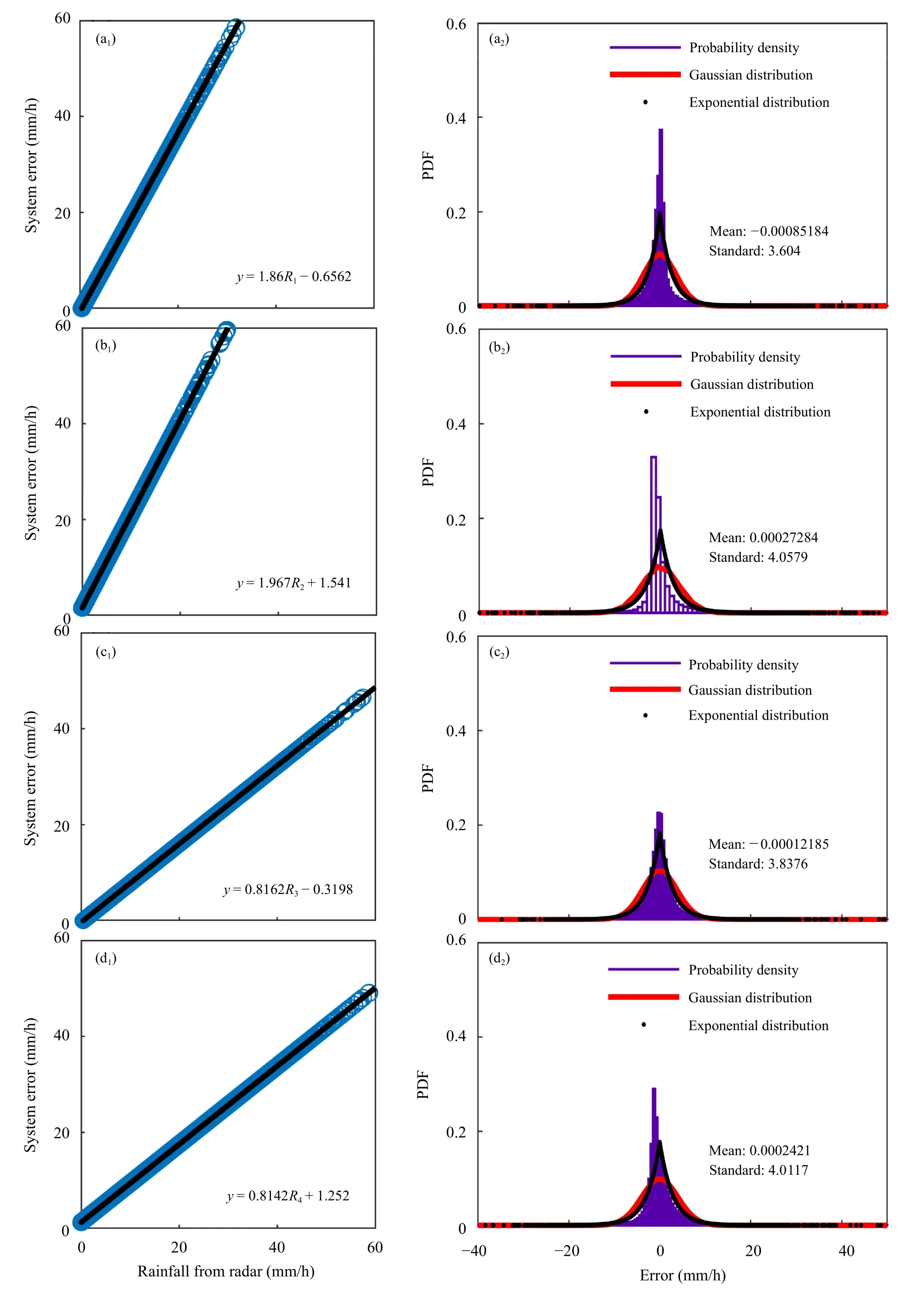
图10 四个测雨公式的系统误差模型(a1—d1)和相应的随机误差模型(a2—d2)Fig.10 Systematic error models(a1—d1)and random error models(a2—d2)for the four rainfall algorithms
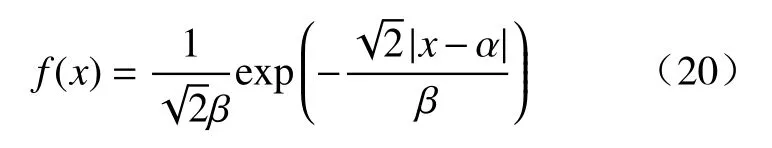
4 最优组合降水公式的提出
为得到最佳雷达定量降水估计效果,基于对4 个雷达测雨公式的误差分析,组合得到最优降水反演算法。图11a—d 分别给出了雷达降水估计算法R(ZH)、R(ZH,ZDR)、R(KDP)和用这3 个公式组合的R(C)在ZH-ZDR空间中的性能。通过雷达估计值与雨量计测量值的归一化绝对误差(NE,式(21))分析各雷达公式定量估计降水的性能。其中ZH和ZDR的分辨率分别取2 dBz 和0.2 dB,NE 的大小用填充的颜色方框表示。
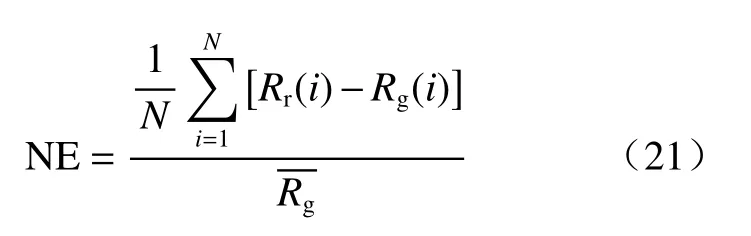
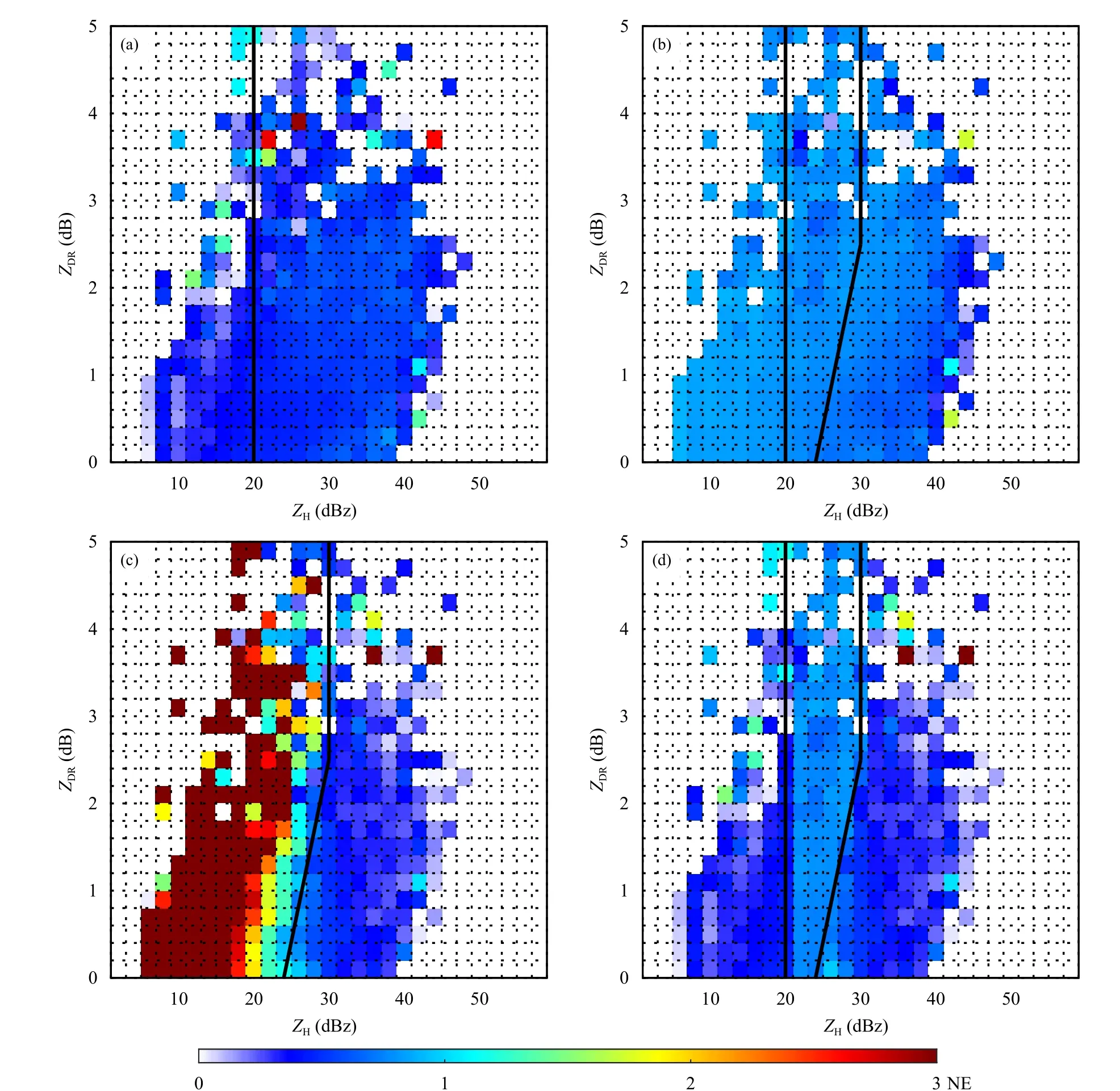
图11 (a)R(ZH)、(b)R(ZH,ZDR)、(c)R(KDP)和(d)R(C)在ZH-ZDR 空间中的每小时定量估测降水的归一化误差(黑线代表三种降雨估计值的阈值,用以计算综合的R(C))Fig.11 Hourly normalized QPE errors of(a)R(ZH),(b)R(ZH,ZDR),(c)R(KDP)and(d)composite algorithm R(C)for the three cases in ZH-ZDR space(black lines represent the thresholds of three rainfall estimators to calculate composite R(C))
图11a—c 中,在ZH<20 dBz 的区域内,R(ZH)的NE 值低于其他两种公式,除个别区域,其他NE值都保持在0.6 以下。当20 dBz<ZH<30 dBz 时(图11b 两条黑线中间的区域)R(ZH,ZDR)的表现比较好,特别是在R(ZH,ZDR)较大时,R(ZH,ZDR)的NE 值保持在0.8 以下。R(KDP)在图11c 中黑线右侧表现最好,大部分值小于0.6。其中黑色斜线部分经过计算为ZDR=0.4167×ZH−10.008。3 种降雨估计算法的性能表明,每种算法都有自己的优点,用单个公式的反演结果并不能很好地显示降雨率,为获得更好的结果,提出了一种综合不同降雨公式的综合算法R(C)。本研究采用的R(C)阈值主要是根据3 种雷达公式在ZH-ZDR空间的最小误差选取的,如图11 中的黑线所示。计算流程如图12 所示。
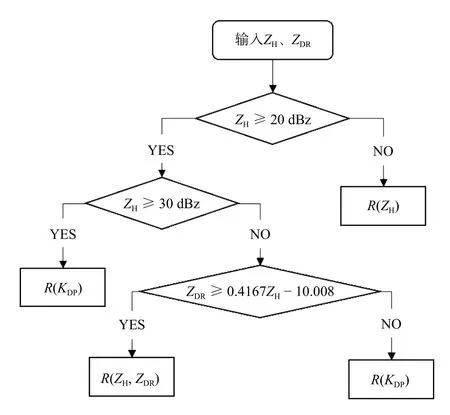
图12 双线偏振雷达降水估测综合方法R(C)算法流程Fig.12 Block diagram illustrating the composite algorithm R(C) for rain-rate estimation by dual linear polarization radar
优化组合算法R(C)的性能如图11d 所示。可以看出,在整个ZH-ZDR空间中,R(C)的NE 值都取到图11a—c 中的最优结果。如图11 所示,在ZHZDR分布区域,每一种降雨估计值的优势都得到了体现,这证明复合算法能够充分利用这3 种降雨估计值,产生最佳的定量降水估计结果。表3 显示了复合反演公式R(C)的性能分析结果。在降雨阈值为0.2 mm/h 时,R(C)的相关系数比单个公式最优值提高了0.027,MAE 降低了0.154 mm/h,RMSE 降低0.952 mm/h,FSE 降低10.57%,每项性能都比单个测雨公式结果更优。虽然随着降雨阈值的增大,每个统计结果增优量在减小,到7.6 mm/h 时各项指标和R(KDP)基本一致,但总体来看,优化组合算法R(C)的性能都比单个公式的统计结果好,说明优化组合算法可以结合4 个测雨公式的优势,从而提高雷达定量估测降水精度。
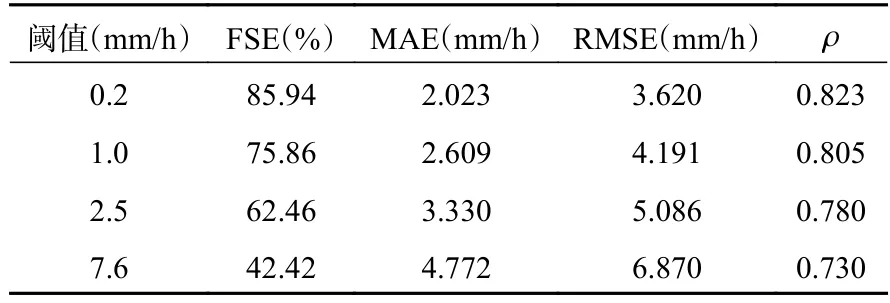
表3 R(C)统计性能分析Table 3 Statistical performance analysis of R(C)
为了分析定量估测降水和优化组合算法的效果,使用2015 年6 月26—28 日降水个例进行分析。2015 年6 月26—28 日暴雨过程是典型的梅雨期降水,暴雨从26 日22 时前后一直持续到27 日22 时前后,近24 h,降水持续到28 日中午才渐止。
现使用Chen 等(2017)中拟合的测雨公式与本研究拟合的测雨公式拟合效果做一对比。Chen 等(2017)使用的也是C 波段雷达,雨滴谱数据为南京地区2014—2015 年夏季观测。如图13所示,其中图13a、b、c 分别是R(ZH)、R(ZH,ZDR)、R(KDP)3 个雷达测雨公式计算雨量与雨量计雨量的对比,黑色的点为Chen 等(2017)中拟合的雷达公式,灰色点为本研究拟合公式。通过散点分布情况和数据统计结果可以看出,两者结果在单个测雨公式中比较接近,R(ZH,ZDR)稍好。图13d 为优化组合R(C)的反演结果,可以看出对于此次降水过程的反演结果和两年降水统计数据的结果一致,R(ZH)的相关高但在雨强较大时反演结果偏差较大,R(KDP)的反演结果在大雨时与雨量计更为一致。而优化组合公式结合了3 个测雨公式在不同阈值的优势,是优化的定量降水估计公式。
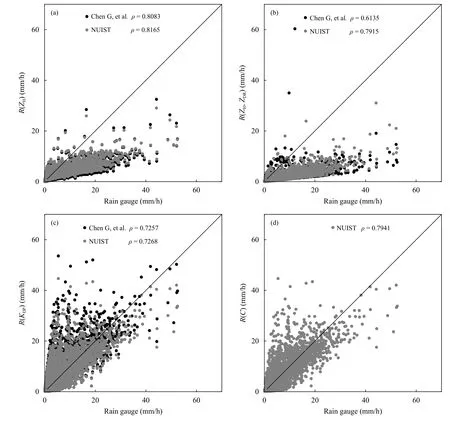
图13 2015 年6 月26—28 日个例NUIST-CDP 雷达定量降水估测公式对比散点(a)R(ZH),(b)R(ZH,ZDR),(c)R(KDP)以及(d)优化组合算法散点对比(其中图a、b、c 中黑色点是Chen 等(2017)拟合的雷达公式结果)Fig.13 Scatter plots of(a)R(ZH)method,(b)R(ZH,ZDR)method,(c)R(KDP)method,and(d)composite algorithm R(C)for 26—28 June 2015(black points in(a),(b)and(c)are the results of radar rainfall formula fitted by Chen,et al(2017))
5 结论
南京信息工程大学C 波段双偏振雷达自2014年架设成功以来,获得了大量降水资料。通过对4 个测雨公式的雷达降水估计数据进行误差分析,得到如下结论:
(1)C 波段双偏振雷达容易受到衰减的影响,因此在使用C 波段双偏振雷达探测资料前要对偏振参量进行预处理,且文中预处理步骤得出的结果能较好改善NIUST-CDP 的数据;在4 个测雨公式中,R(ZH)在小雨时有很大的优势,但随着降雨阈值的增大,到达中雨以后,R(KDP)的优势得以突显。
(2)在以雨量计作为真值评估雷达数据质量时,雨量计和雷达空间不匹配造成的误差不能忽视,且其随着阈值的增大而增大,在雷达分辨率平均为0.33 km2的像素内,R(KDP)的点面误差方差占总误差方差的百分比从0.2 mm/h 阈值时的0.5%增长到7.6 mm/h 阈值时的17%。因此,在雷达可分辨面积较小时分析雷达定量估计测雨误差需计算并剔除点面误差。
(3)对雷达估测降水进行误差建模,将其分为系统误差和随机误差,可以发现,雷达近地面降水估计的系统误差和雨强成正比,且呈线性函数形式。在消除了系统误差带来的影响后,随机误差呈近似正态分布,利用高斯模型和双指数模型分别进行建模,发现双指数模型能更好模拟随机误差分布。
(4)基于对每个测雨公式在不同阈值上的统计性能和误差分析,结合在双偏振信号ZH-ZDR空间中雷达测量值和雨量计归一化绝对误差的分布,利用4 个测雨公式在不同阈值上的优势,得到的优化组合算法R(C)。相对单个降水公式,优化组合算法能产生最佳的定量估测结果,明显提高了定量降水估计的准确度和稳定性。
文中通过对4 个测雨公式误差的分析,发现含有ZH的公式系统误差增长较快,说明R(ZH)和R(ZH,ZDR)在测量大雨时准确度较低,而含有KDP的公式系统误差增长较慢,可以在大雨时提供相对准确的测雨结果。另外,含有ZDR的公式随机误差在0 附近的分布较为集中,体现了增加ZDR测雨的优势。这些均说明不同降水公式各有不同优缺点和误差性能,而优化组合是一种有效的提高双偏振雷达降水估计精度的方式。另外,本研究中的雷达降水估计误差量化建模为以后降水算法优化、不确定性建模、数据同化以及多源降水数据融合等提供了研究基础。

