一种基于随机超曲面的扩展目标形状评估方法
徐 寒,韩玉兰,曹晓峰
(宁夏大学 物理与电子电气工程学院,宁夏 银川 750021)
衡量一个算法的好坏往往需要合理的评估方法,因此评估方法是至关重要的。在目标跟踪领域,一般的评估方法是通过计算目标的真实状态和目标估计状态之间的误差来实现的。以点目标为例,通常是使用目标的真实状态和估计状态的均方根误差(RMSE),作为状态估计性能好坏的指标[1]。随着传感器精度的不断提高,点目标假设不再成立。在实际情况下,目标在每个时刻可能会占据多个分辨单元,存在多个量测源,产生多个量测,这样的目标称之为扩展目标。扩展目标的多个量测不仅可以对目标的运动学状态进行估计,还可以提取目标的形状信息。因此,对扩展目标的形状估计性能进行评估是十分重要的。
当扩展目标为规则形状时,滤波器对形状的估计性能可由其主要参数的RMSE进行度量。例如,针对Koch提出的基于随机矩阵(RM)算法[2],可以采用长轴、短轴、方向的RMSE来度量滤波器对椭圆形扩展目标的形状估计性能,但这种方法不适用于不规则形状[3]。为了能够度量不规则形目标的估计形状,部分学者将计算机视觉和图像处理领域的交并比(IoU)概念引入到扩展目标跟踪中,作为对形状的估计性能指标。但是IoU方法只采用了面积的交并比,对形状的相似度不能够很好地表示,如椭圆形和长方形的IoU值也有可能很大[4]。因此,IoU并不能很好地描述目标的估计形状和真实形状的差异。部分学者采用拟Jaccard距离来对其进行评估,但是在计算最短距离和最长距离时将估计形状和真实形状看作一个整体,这无疑忽略了两者的独立性[5-9],导致了即使估计的形状和目标的真实形状很相似,但是大小不同,得到的拟Jaccard距离会偏大,因此该方法也存在缺点。
为了解决上述问题,本文在Baum提出的随机超曲面模型(Random hypersurface model-RHM)的基础之上,提出了一种基于径向函数的扩展目标形状估计的评估方法。提出的方法对每一个角度上估计距离和到目标边界的真实距离进行了比值运算,然后对所有角度下得到的集合求解标准差,利用该集合中数据的离散程度来对扩展目标的估计结果进行评估。实验表明,提出的方法能够较好地描述估计形状和真实形状之间相似度的变化。
1 扩展目标的形状建模与跟踪
Baum提出RHM可以描述星凸形目标的形状,对符合星凸形形状条件的不规则的扩展目标直接建模。星凸形可以定义:如果集合S⊂SN当中的任意一个点到质心m的线段上所有的点都仍属于此集合,则集合S形成的形状称为星凸形[10-12]。对于星凸形目标,可以通过径向函数来描述其形状,其可以展开成如下的傅里叶级数形式:
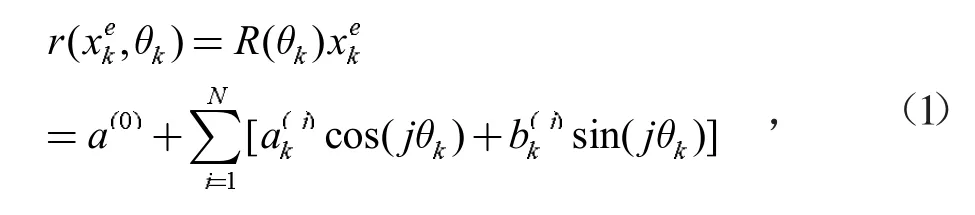
其中,θk是k时刻质心与边界点的夹角,R(θk)是傅里叶系数,ak和bk是组成目标形状参数的分量。

加入缩放因子s,s∈(0,1],星凸形扩展目标形状S(xk)可以由下面式子来表示:

其中,e(θk)为单位向量,,分别表征了扩展目标在k时刻的坐标、速度。量测方程可以表示:

其中,h是非线性函数,vk,l是量测噪声,sk,l是第l个量测点的缩放因子。
2 基于径向函数的估计形状评估方法
对扩展目标的形状评估可以转化为求解2个封闭曲线的相似度问题。在跟踪扩展目标时,如果扩展目标的估计中点mk在真实目标的内部,则扩展目标的真实形状和估计形状的边界都可以用径向函数来表示,基于径向函数的扩展目标形状估计评价算法有如下解释。
以估计中点mk为坐标原点建立平面直角坐标系,并引出一条射线,与所建立的平面直角坐标系横轴的正半轴的夹角为θ,到真实形状的边界和估计形状的边界的距离分别是Aθmk和Bθmk,由于星凸形在一个角度上只有一个确定的点,当θ确定时,有:

dθ为在角度θ上真实边界到估计边界的比值,由实际几何含义已知,当比值dθ>1时,那么在角度为θ处,真实形状是大于估计形状的,反之则是小于估计形状。借助角度均匀离散采样的思想,在θ上均匀地取N个值,第N个角度用θN表示,将每个角度θ对应的比值构成的集合定义为Dk,该集合包含了每个角度下的估计形状和真实形状的相似度。如果该集合中的元素整体变化不大,则说明估计形状和真实形状很相近。该集合的均值可以表示:

为了描述这种变化,不妨采用总体标准差来表示:

由概率统计学可知,总体标准差σk越小,则说明集合Dk中的元素离散程度越低,真实形状和估计形状的相似度越高;若总体标准差σk的值越大,则说明真实形状和估计形状的相似性很差。
由于星凸形的扩展目标的建模方式为上述的RHM,形状估计中的径向函数可以直接使用。扩展目标的估计形状用表示,目标的真实形状用S(Cx)k表示,分别通过径向距离函数来表示,即:

其中,θk∈[0,2π),采用角度均匀离散采样的方式,将上式的连续集替换成离散集。
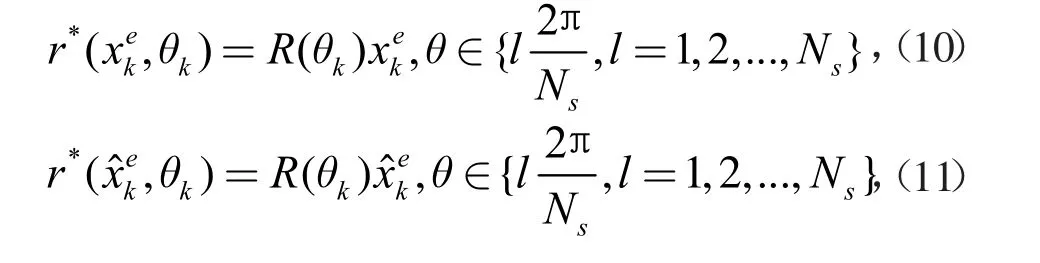
上式中,NS为采样个数,将上述2个式子带入到公式(7)中,有:
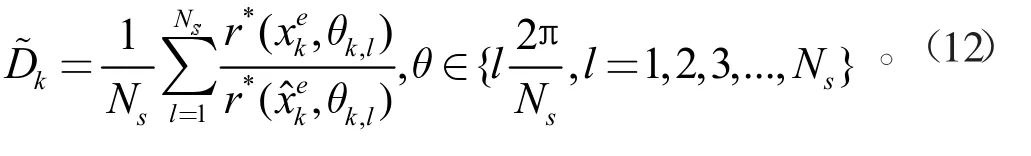
将式(12)直接带入到式(8),可以得到基于径向函数的扩展目标形状评估结果。
3 仿真与对比性能评估
为了证明提出的评估标准有效性,将提出的算法与拟Jaccard距离算法、IoU算法在2个不同场景下进行对比实验,从而说明提出方法的有效性。
本节使用的扩展目标为一个十字形目标,如图1所示。目标的初始状态为x=[20,10,10,10]T。目标在二维笛卡尔坐标平面内做匀速直线运动,设初始估计的目标形状为半径等于3的圆形。每一个时刻获得的量测的个数为服从参数等于20的泊松分布,采样周期间隔T=1 s。
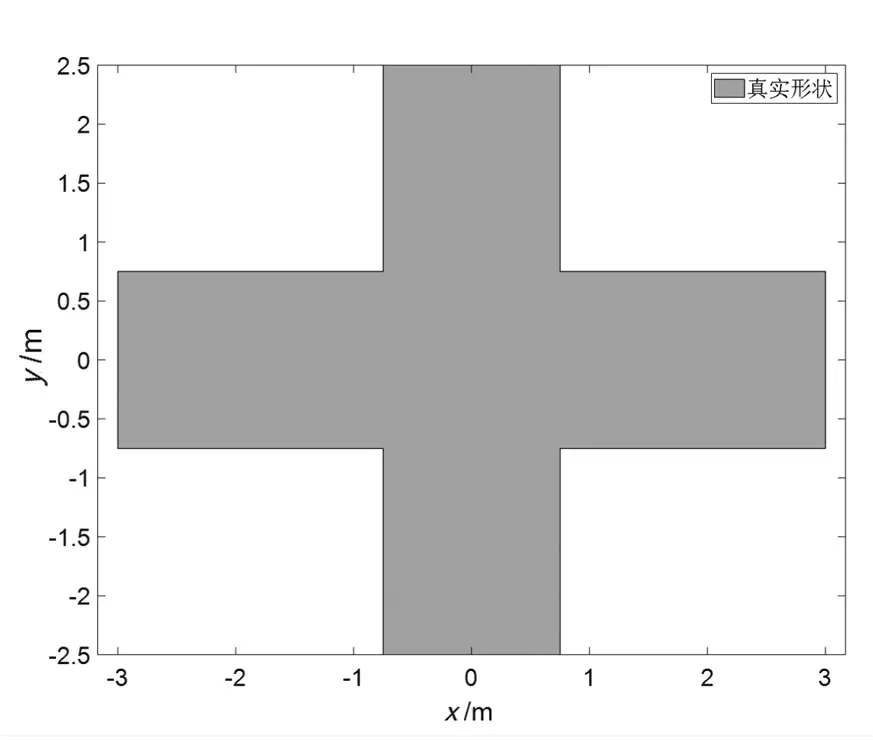
图1 扩展目标的真实形状
众所周知,在扩展目标跟踪的过程中,传感器噪声对扩展目标的形状估计效果有着很大的影响。如果传感器噪声较小,那么对扩展目标的形状估计效果应该更好,反之亦然。若对同一个目标在不同噪声下获得的形状估计进行评估,那么传感器噪声较小的估计形状应该会有更好的指标。分别给出2种不同噪声情况下扩展目标跟踪的形状估计效果。扩展目标跟踪的仿真结果如图2所示,局部放大图如图3所示,3种不同评估算法对扩展目标在各个时刻的评估结果,如图4所示。
图2、图3中,实线是低噪声情况下得到的估计形状,虚线是高噪声情况下得到的估计形状。在不同噪声的情况下,每一个时刻获得的量测数量是相同的。基于这一场景,考察的是形状评估算法的可靠性。从图4可以看出,3种算法均具有较好的可靠性。
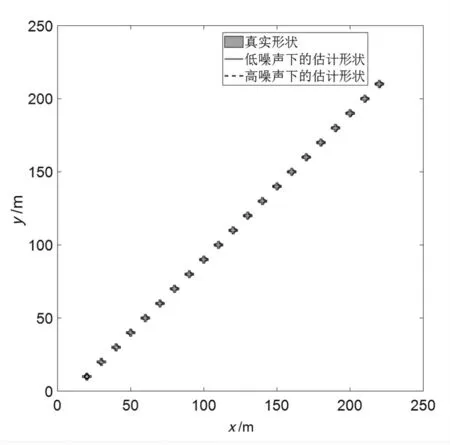
图2 场景1中的星凸形跟踪估计图

图3 图2的局部放大图
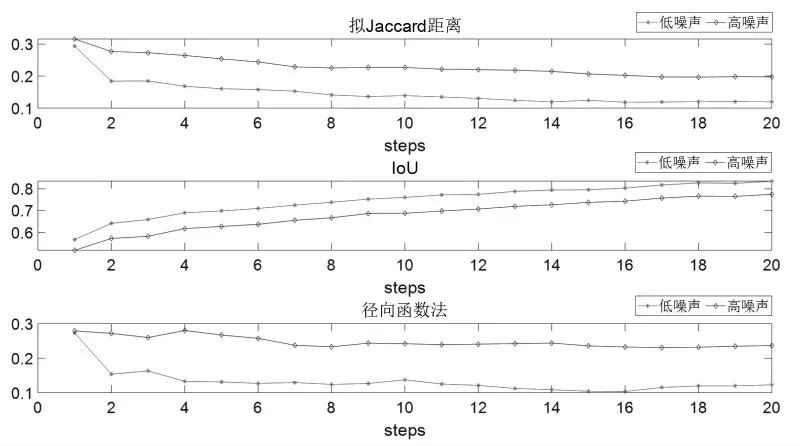
图4 3种不同算法在不同噪声影响下的形状估计评估图
在低噪声情况下,为了将每种算法较前一个时刻的优化效果量化出来,不妨采用优化率对每一个时刻的优化效果进行量化,结果如图5所示。
从图5可以看出,采用本文提出的评价方法具有更高的数值差异,这说明提出的方法具有更高的灵敏性。在第16-17时刻,估计结果有了较大的负优化,量化后约为-11.4%。为了找到负优化的原因并验证提出方法的合理性,查找16-17两个时刻的估计形状,找到两个时刻下径向函数中比值偏离均值较大的所在角度,二者差异如图6所示。

图5 3种算法在各个时刻的优化率
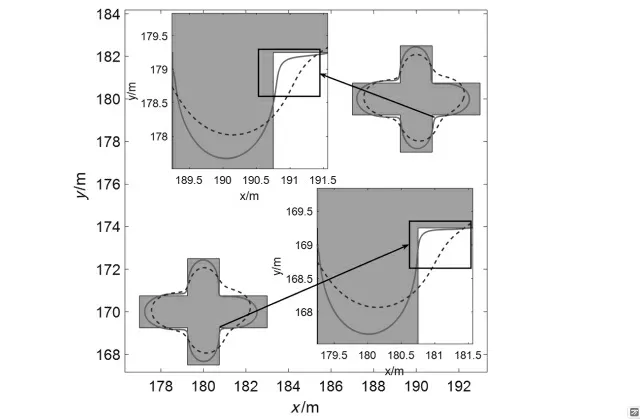
图6 目标在16-17时刻的局部效果图
从图6可以看出,在低噪声情况下(实线),在箭头所指的部分,第16个时刻(右下)得到的估计形状,比第17个时刻得到的估计形状(左上)效果更贴近目标的真实形状,正是由于这一点的偏差,使得在第17个时刻产生了负优化。而其他2种算法无法将这一细节通过数值来准确地表示出来,由此可见本文提出方法的灵敏度与可靠性。
以上的仿真实验表明,本文提出的基于径向函数的扩展目标形状估计的评估算法,是合理且有效的,它对形状的变化具有高度的灵敏性。
4 结束语
本文对基于随机超曲面的扩展目标跟踪,提出了一种基于径向函数的形状估计评估方法,作为扩展目标跟踪中的形状估计好坏的指标。实验证明了该方法是一种有效的度量指标,相比较IoU和拟Jaccard距离方法,提出的方法具有好的灵敏性,对目标的细微的变化也可以表示出来。下一步工作拟将其推广到非星凸形扩展目标跟踪中。

