含尘气泡形变及相互作用对颗粒脱除率的影响

梁 纤， 潘伟童， 陈雪莉

（ 华东理工大学国家能源煤气化技术研发中心，上海煤气化工程技术研究中心，上海 200237）

煤气化作为现代煤化工的龙头，气化界区的合成气中细灰颗粒含量需严格控制在1 mg/Nm3以下[1]，因此煤气化粗合成气中细灰的高效脱除尤为重要。在已工业化应用的煤气化技术中，合成气中细灰的脱除多采用湿洗分离方法，而鼓泡接触型湿式分离又是其中的首选[2]。含尘气泡是鼓泡接触型湿式分离体系中的单元集尘体，对含尘气泡的运行特性进行深入研究，将为细颗粒的高效脱除和鼓泡洗涤器的优化设计提供重要的理论支撑。

在前人的研究中，多将集尘气泡分为两部分讨论：气泡的单独上升运动与理想化流场下气泡携带颗粒的上升运动。1976 年，Grace 等[3]给出了单个不含尘气泡上升的形状谱图，Bhaga 等[4]对气泡图谱进行了完善。之后又有许多学者对单个气泡进行了研究，包括上升速度、界面变化、添加表面活性剂等[5-8]。对于同步上升的两气泡，其受力和运动情况与单气泡不同，其中研究最多的是并行双气泡的上升过程[9-11]，对其他组合方式双气泡的共同上升过程也有研究[12-14]。

在系统研究鼓泡体系中气液两相相互作用机制的基础上，学者们开始关注气液固三相间相互作用机制。颗粒在气泡内部的运动传输主要受不同的传输机制控制，如惯性扩散、布朗扩散、对流等机制[15-17]。1964 年Fuchs 等[18]通过实验研究首先预测了气泡在上升过程中会出现内部循环，该循环将大大增强粒子的扩散和惯性作用，并据此提出了球形上升气泡内颗粒脱除的数学模型。Li 等[19]运用CFD 计算模拟软件对气液固三相流态化系统建立了模型，并模拟了液固两相床中单气泡上升过程的颗粒夹带和尾迹脱落现象，结果表明其所建立的模型与文献报道结果吻合良好。Xu 等[20]运用电声技术考察了不同粒径和润湿性的石英及玻璃微珠颗粒在振荡气泡中的分离过程，结果发现气泡-颗粒聚集体在高黏度液体中的稳定性与颗粒的动态接触角有关。Pan 等[21]通过流体体积-离散相模型（VOF-DPM）耦合法模拟研究了含尘气泡在静止液体中上升时的形变特征，分析了气泡形变对颗粒脱除的影响，结果表明气泡形变能够增强微细颗粒的脱除率。

综上分析可知，关于含尘气泡上升过程的动态变化与颗粒脱除机制间的内在关系尚不明晰，且大部分模拟研究仅是基于二维物理模型，无法反映含尘气泡上升过程动态变化的全貌。基于此，本文将通过建立三维物理模型模拟研究静止液体中不同含尘气泡上升过程对颗粒脱除的影响。

1 数值模拟

1.1 物理模型

基于二维物理模型的局限性，本文将采用三维物理模型对含尘气泡上升过程进行模拟研究。三维物理模型如图1 所示，图中显示的为单气泡，双气泡时的计算域模型与此相同。相；α=0 时，表示该区域没有该相；0＜α＜1 时为混合物[23]。不可压缩流体的流动控制方程如下：

连续性方程：

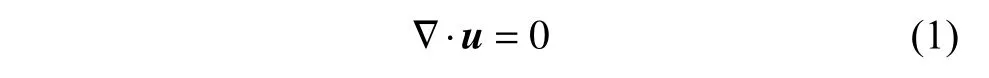
动量方程：

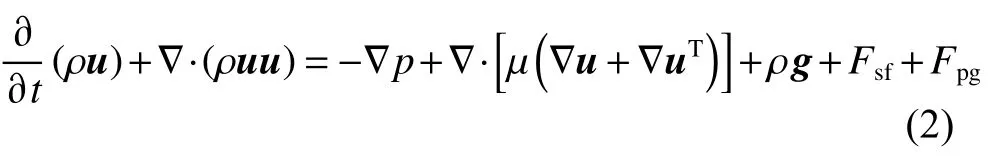
其中u,ρ 分别为计算相的速度和密度；Fsf是表面张力；Fpg是来自颗粒的作用于流体相的动量交换力，作用于含有颗粒的晶胞。在VOF 模型中通过求解整个区域内的单一的动量方程，得到由各相共享的速度场，而动量方程取决于通过所有相的容积比率。

体积分数方程：

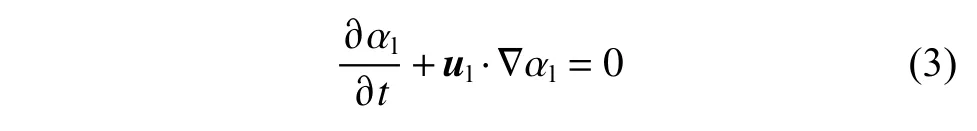
计算域中充满了水(温度25 ℃，密度9.982×102kg/m3，黏度10-3Pa·s，表面张力系数0.072 8 N/m)。初始时在计算区域底部中心放置一个含尘气泡(气体密度1.225 kg/m3，气体黏度1.789×10-5Pa·s；含尘颗粒粒径分别为1 μm 和2.5 μm，密度2×103kg/m3)。模拟计算时根据气泡尺寸大小调整计算域的宽度，计算域的高度始终保持在60 mm，网格划分使每个气泡内至少包含10 000 个单元以确保计算的精确性。

模拟计算基于以下几点假定：

(1) 气体被认为是不可压缩的。

(2) 颗粒的脱除通过水膜擦洗方式实现，当颗粒到达液体体积分数0.5 的区域即认为被脱除(在已有文献报道中认为空泡体积分数大于0.5 的部分是气泡[22])。因此本文忽略了液体-颗粒之间的相互作用和颗粒通过液膜时的界面力。

(3) DPM 模型将微米级颗粒视为运动质点，忽略颗粒间的相互作用及其对气相体积的影响。

1.2 数值模型

1.2.1 流体相模型 模拟中气相与液相均视为连续相，通过欧拉法计算其连续性方程与动量方程，数值模型采用VOF 模型。VOF 模型是一种表面跟踪技术，用于处理没有相互穿插的多相流问题，通过求解一组动量方程并在整个计算域内跟踪每一相的体积分数(α)来区分两相，当α=1 时，表示该区域充满该

其中，下标l 表示每个控制体积中的液相，由于所有相的体积分数之和应为1，因此可以根据式（4）计算气相的体积分数( αg)：

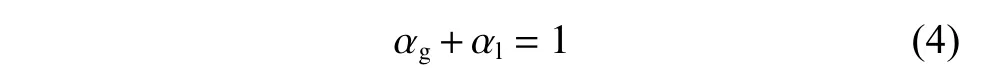
表面张力是一种作用在表面上的力，它平衡了内部放射状的分子引力和跨过表面的放射状的外部压力梯度。表面张力对处于水中的气泡的变形影响显著。另外，Fluent 中表面张力模型采用的是Brackbill等[24]提出的连续表面力模型。

1.2.2 固体相模型 由于固体颗粒的体积分数较低，将其视为离散相，采用拉格朗日方法，选用DPM 模型，并假定不考虑颗粒-颗粒之间的相互作用以及颗粒体积分数对连续相的影响。Fluent 中通过积分拉氏坐标系下的颗粒作用力微分方程来求解离散相颗粒的轨道。颗粒的作用力平衡方程(颗粒惯性＝作用在颗粒上的各种力)在笛卡尔坐标系下的形式为（x方向）：

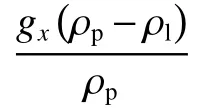
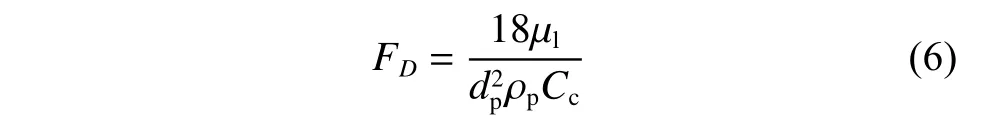
其中μl为液体动力黏度，dp为颗粒粒径，Cc为Stokes'曳力公式的Cunningham 修正(考虑稀薄气体力学的颗粒壁面速度滑移的修正)，其计算公式为：

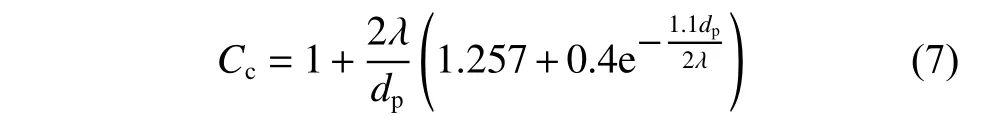
其中λ为气体分子平均自由程：

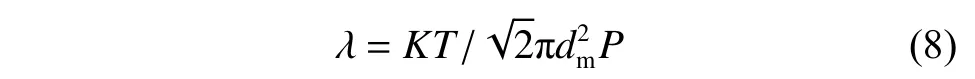
式中T为温度；dm为空气气体分子的直径，dm=3.5×10-10m；P是气相压力。由式（8）计算得平均自由程λ=6.9×10-8m。

在整个计算过程中，颗粒脱除率η可定义为：

式中Np是该时刻气泡内剩余颗粒数，Np0是初始时刻气泡内总颗粒数。

1.2.3 气泡上升形态验证 图2 所示为单气泡上升形态实验装置。透明有机玻璃水箱尺寸为200 mm×200 mm×600 mm，有机玻璃板厚度为1 cm，箱内装有适量的纯水。实验装置中的气泡发生部分主要由空气注射器、测量管道、可旋转调节的杯罩和单向阀组成。在实验装置中分别进行了尺寸为6、8、10、12 mm气泡的上升实验。

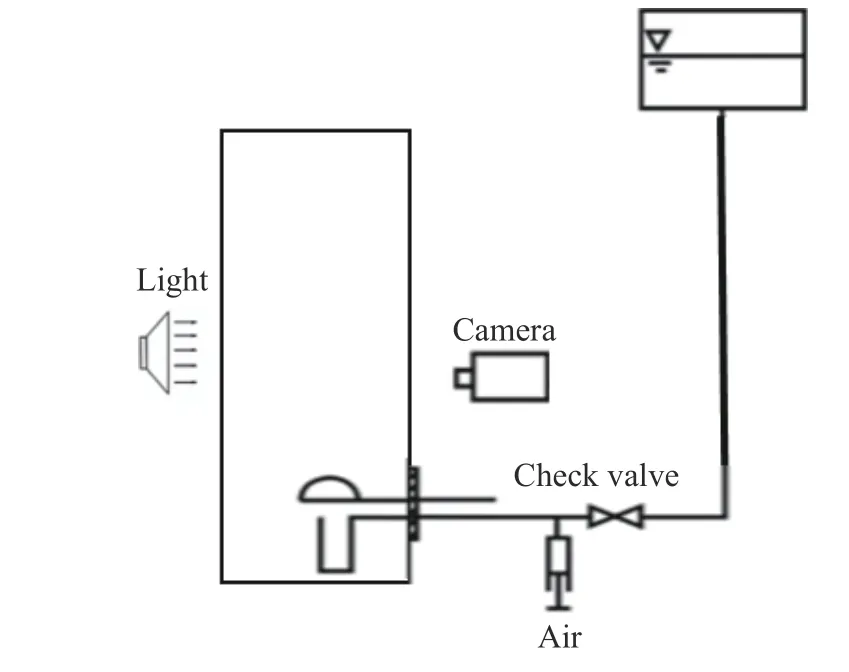
图2 单气泡上升实验装置Fig. 2 Device of single bubble rise experiment

图3(a)所示为实验拍摄的气泡形态变化，气泡尺寸从左至右依次为6、8、10、12 mm；图3(b)所示为模拟条件下含尘单气泡在上升过程中的形态变化结果，对比图3(a)可知，与实验结果基本一致。

图3 气泡形变的实验结果（a）和模拟结果（b）比较Fig. 3 Comparison of bubble deformation experimental results (a)with simulation results (b)

2 结果与讨论

2.1 含尘气泡上升过程

2.1.1 含尘单气泡上升过程 模拟计算了不同尺寸(6、8、10、12、14 mm)含尘气泡的上升过程，气泡中颗粒粒径均一，分别为1.0 μm 和2.5 μm，结果如图4所示。图4 中颗粒粒径为1.0 μm，红色部分为颗粒(非颗粒实际大小，为了便于观察将颗粒放大处理)。

由图4 可以看出，对于给定的气泡尺寸范围，气泡在上升过程中均发生形变，且形变总是从气泡下表面向内凹陷开始，最终都发展成扁椭球的形状，但随着气泡尺寸增大，气泡的形状变化越来越稳定。尺寸较小(6～8 mm)的气泡呈现出复杂的变形和不规则的振荡，形变强度较高；当气泡尺寸大于12 mm时，形状变化被抑制，当下部凹陷变为“头盔”状后，气泡由于倒流涡旋而使其尾部变平，随后成为带有凹入底部的球帽并上升。

图4 不同尺寸含尘单气泡上升过程Fig. 4 Rising process of dust-containing single bubbles of different sizes

2.1.2 并行含尘双气泡上升过程 单气泡及其上升过程动力学的研究已较多，而在双气泡共同上升过程中，由于气泡间的相互作用，其形变必然不同于单气泡，从而对气泡内颗粒的脱除产生影响，因此有必要对双气泡的共同上升过程进行模拟。双气泡共同上升的模式较多，其中等尺寸并行上升气泡是较典型且有代表性的一种。本文模拟计算了不同尺寸(6、8、10、12、14 mm)含有1.0 μm 颗粒的并行双气泡上升过程，单个气泡中颗粒数量与前文相同，双气泡间初始间距均为5 mm。图5 所示为不同尺寸含尘双气泡上升过程示意图，图中红色部分为颗粒(非颗粒实际大小，为了便于观察将颗粒放大处理)。

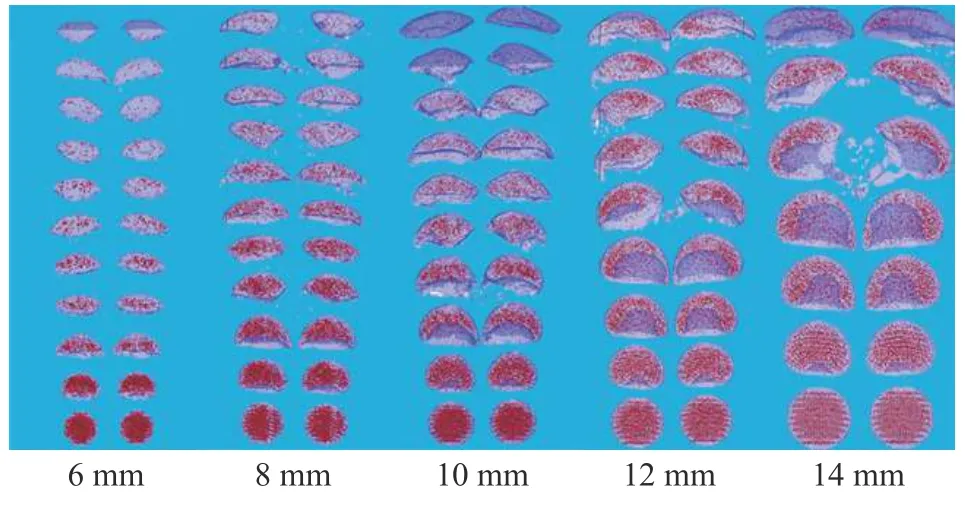
图5 不同尺寸并行含尘双气泡上升过程Fig. 5 Rising process of parallel dust-containing double bubbles of different sizes

计算域高度一定，在固定初始间距为5 mm 情况下，并行双气泡在上升过程中发生了形变但均未发生聚并；尺寸较小的气泡形变与单气泡上升时形变相似，气泡首先变化为扁椭球形，呈摇摆状上升，气泡对之间呈现出靠近-分离-靠近-分离的趋势。分析认为，气泡一旦开始上升，周围流体将产生涡旋，伴随涡旋脱落将形成尾流区，尾流内流体上升速度较大，随着尾流的增长，气泡的摇摆运动使得两个气泡可以正向运动也可以反向运动。并行上升的大尺寸气泡因气泡间相互作用较强，使其气泡形变与单气泡上升时的形变显著不同。上升初期，两气泡间交汇处形成剪切变稀流体区域，该黏度特征推动气泡在水平方向相互靠近，而靠近后的大尺寸气泡对间的涡旋挤压作用增强，气液界面向两侧凹陷，气泡对被推动分离，呈现V 型对称式分布；随间距的增加，内侧涡旋作用减弱，气泡对再次靠近。

2.2 不同含尘气泡上升过程中颗粒的脱除率

2.2.1 含尘单气泡上升过程中颗粒的脱除率 图6 所示为含尘单气泡上升过程中颗粒脱除率随气泡尺寸的变化，气泡中颗粒粒径分别为1.0 μm 和2.5 μm。

由图6 可知，当颗粒粒径为1.0 μm 时，随着气泡尺寸增加，颗粒的脱除率单调下降；当气泡中颗粒粒径为2.5 μm 时，不同气泡上升过程中颗粒的脱除率几乎都高于粒径1.0 μm 颗粒的脱除率，且随气泡尺寸增大颗粒脱除率曲线不再呈单调变化，而是在气泡尺寸为8 mm 左右时出现峰值(97.5%)。综上说明，小尺寸气泡中的颗粒更易脱除；对不同粒径的颗粒，存在使其高效脱除的适宜的气泡尺寸范围，超过该范围，则颗粒脱除率显著下降。

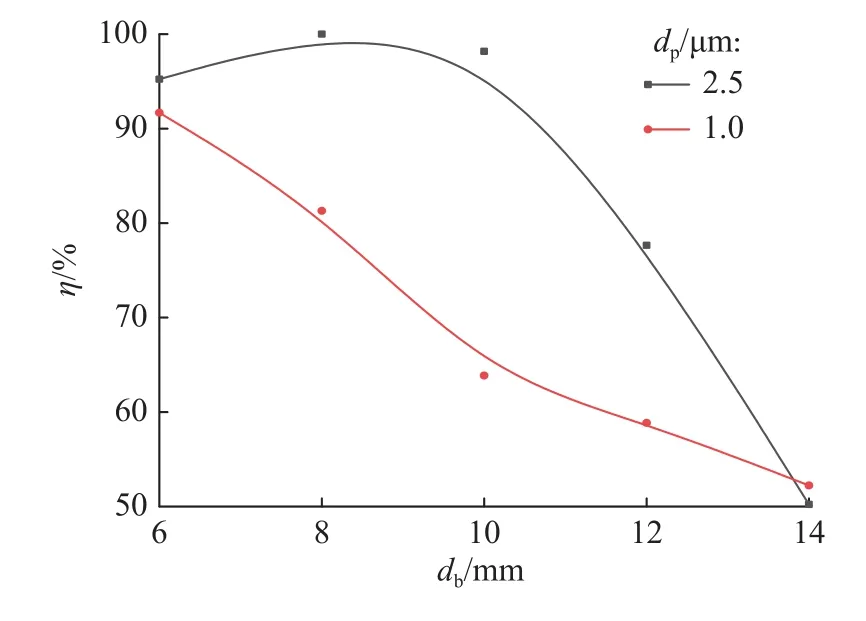
图6 不同尺寸含尘单气泡中颗粒的脱除率Fig. 6 Removal efficiency of particles in different sizes of dustcontaining single bubbles

图7 所示为含不同粒径颗粒时单气泡上升过程的形态变化。由图可以看出，气泡中颗粒粒径增大对其上升过程形态变化几乎没有影响，颗粒脱除率不同的原因在于颗粒本身，粒径较大的颗粒具有更大的惯性，更容易被脱除。

图7 含不同粒径颗粒的单气泡上升过程形态变化Fig. 7 Morphological change of dust-containing single bubbles of different sizes during the rising process

图8 所示为含两种粒径颗粒的不同尺寸单气泡内颗粒脱除过程。由图8 可以看出，气泡尺寸越小，其内颗粒在上升初期脱除速率越快，在较短时间内即能达到较高的脱除率；当颗粒粒径由1.0 μm 增大至2.5 μm 时，6、8、10 mm 3 种尺寸气泡呈现出不同的脱除趋势，8 mm 和10 mm 气泡中的颗粒脱除更快，这与图6 中所表现的颗粒脱除率趋势相符合。从图8 还可以看出，对于所有尺寸的气泡，颗粒的脱除速率并未随时间的增加而单调减小，在某些时刻会增大，该现象可在图9 中直观体现。

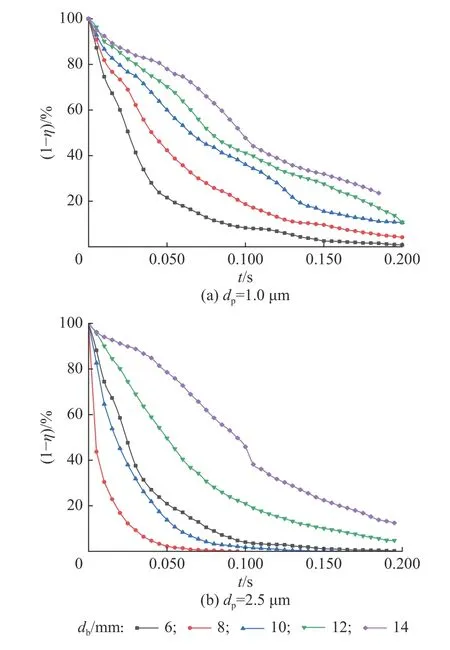
图8 不同尺寸单气泡内颗粒脱除过程Fig. 8 Removal of particles in single bubbles of different sizes

图9 所示为含两种粒径颗粒时，不同尺寸气泡在上升过程中的颗粒脱除速率。由图8 和图9 可知，在气泡上升过程中，颗粒的脱除速率并不单调，不同尺寸气泡存在快速脱除时段且各不相同，总体表现为6～8 mm 气泡中颗粒脱除速率变化相似，10～12 mm气泡中颗粒脱除速率变化相似，这与气泡上升过程中的变形规律相符。

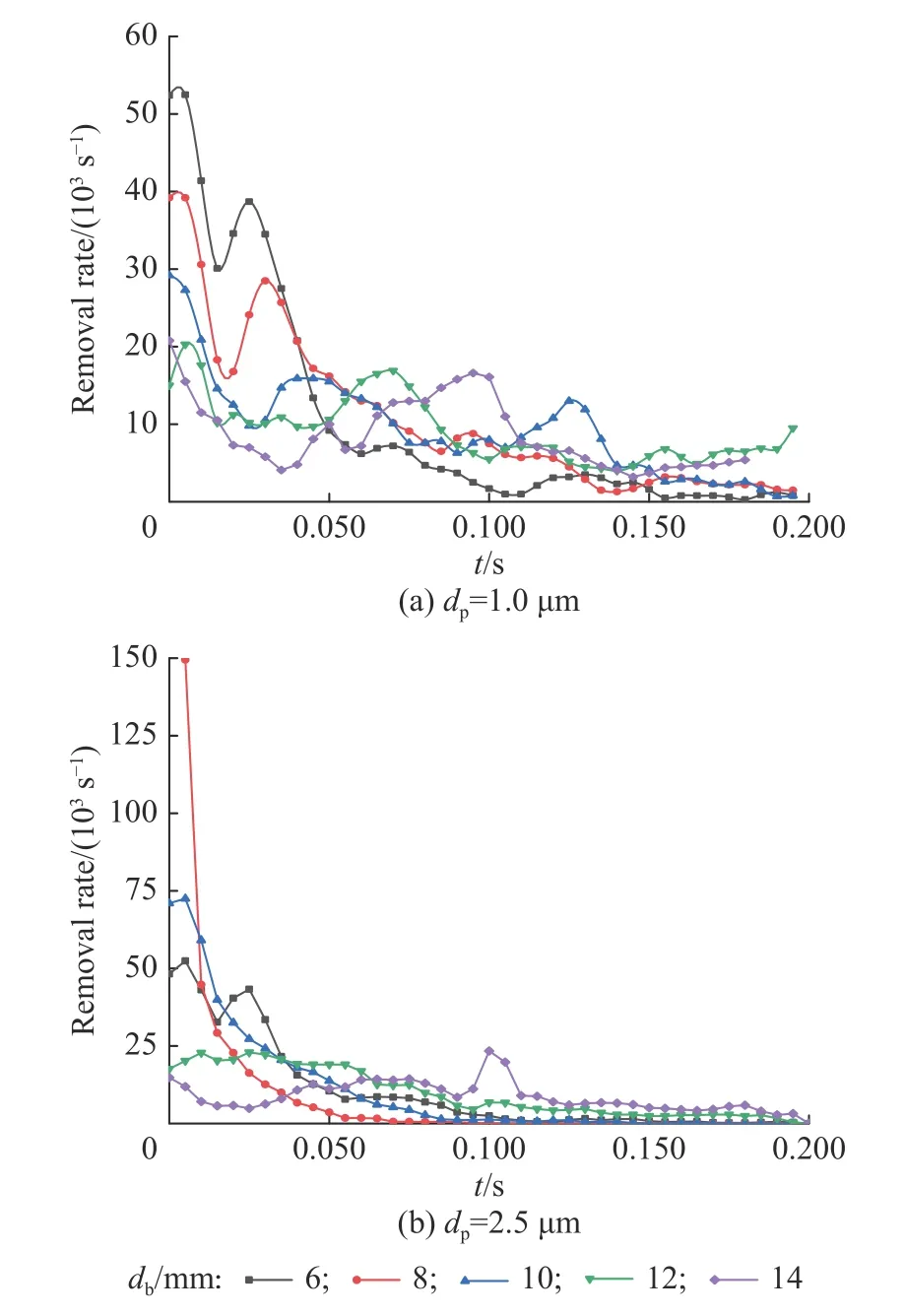
图9 颗粒的脱除速率随时间变化Fig. 9 Removal rate of particles over time

为探究快速脱除阶段的机理，取各尺寸气泡快速脱除时段内颗粒浓度分布并作图(气泡中颗粒粒径为1.0 μm)，结果如图10 所示。结果表明，快速脱除阶段为气泡由下凹陷球体变化为扁椭球的阶段，这可能是由于该阶段气泡形变最显著，在变形阶段，由于气泡涡旋的变化，气相对颗粒的作用力方向(式5 中Fg)改变，从而加快颗粒与气液界面发生碰撞，与已报道文献[21]中提出的变形对颗粒脱除有增强作用相符。

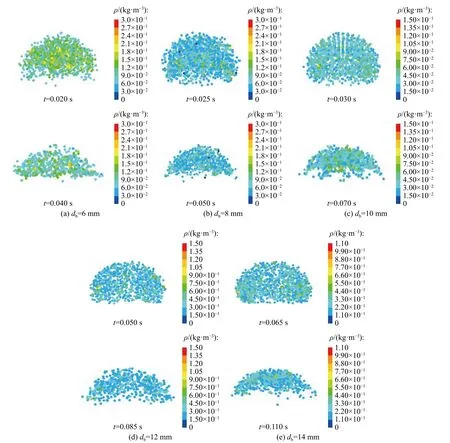
图10 不同上升时间单气泡内颗粒浓度分布变化Fig. 10 Changes of particle concentration distribution in single bubbles with different rise time

2.2.2 并行含尘双气泡上升过程中颗粒脱除率 图11所示为并行含尘双气泡上升时粒径为1.0 μm 颗粒的脱除过程。由图可知，8 mm 与10 mm 并行含尘双气泡的脱除过程基本相同，这与前文含尘单气泡中颗粒的脱除过程不同(8 mm 含尘单气泡具有显著优势)。该现象表明在一定气泡尺寸范围内，两气泡的共同作用可以增强脱除率；但随着气泡尺寸进一步增大，该增强作用减弱。

图11 不同尺寸并行含尘双气泡内颗粒脱除过程(dp=1.0 μm)Fig. 11 Removal of particles in parallel dust-containing double bubbles of different sizes(dp=1.0 μm)

图12 所示为不同尺寸含尘单气泡与并行含尘双气泡上升过程中粒径为1.0 μm 颗粒的脱除率。由图可知，不同尺寸并行含尘双气泡中，粒径为1.0 μm颗粒的脱除率并未全部高于或低于含尘单气泡，而是交错变化。对含尘单气泡和并行含尘双气泡而言，小尺寸(6 mm)气泡均表现出较高的脱除率；但从8 mm 左右的气泡开始，并行含尘双气泡中1.0 μm 颗粒的脱除率增加，气泡尺寸在10 mm 左右时1.0 μm 颗粒的脱除率达到最大，随后随气泡尺寸增大，1.0 μm颗粒的脱除率快速降低，甚至低于含尘单气泡中颗粒的脱除率。

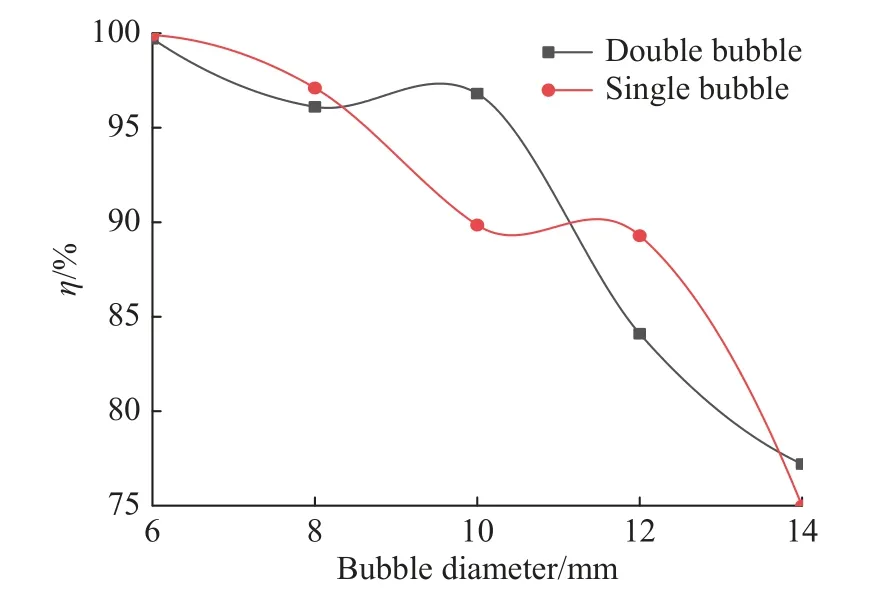
图12 不同尺寸含尘单气泡与并行含尘双气泡颗粒脱除率(dp=1.0 μm)Fig. 12 Removal efficiency of particles with different sizes of dust-containing single-bubble and parallel dustcontaining double bubbles(dp=1.0 μm)

图13 所示为颗粒粒径为1.0 μm 时，并行含尘双气泡颗粒脱除速率曲线。由图可知，各尺寸气泡均有快速脱除阶段，6 mm 气泡在上升初期即快速脱除并达到高脱除率；8 mm 气泡与10 mm 气泡表现出相似的脱除速率变化趋势，12 mm 气泡与14 mm 气泡的脱除速率规律相似。由前文可知，快速脱除的原因一方面是由气泡发生剧烈变形所造成，而另一方面必然与双气泡间的相互作用相关。

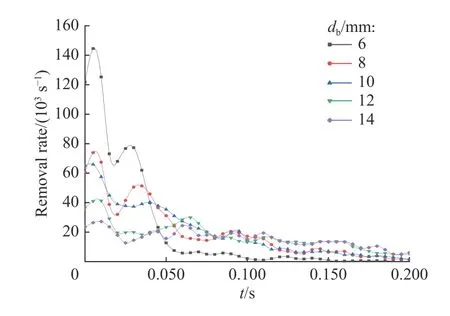
图13 并行含尘双气泡颗粒脱除速率随时间变化(dp=1.0 μm)Fig. 13 Removal rate of parallel dust-containing double bubbles varies with time(dp=1.0 μm)

图14 所示为8 mm 含尘双气泡在t为0.020～0.045 s(图13 中脱除速率增加阶段)与t为0.045～0.065 s(图13 中脱除速率减小阶段)的气泡形态与相对运动趋势。由图可知，当t为0.020～0.045 s 时，两气泡相互靠近，呈现出倒八字形；当t为0.045～0.065 s时，在前时段内两气泡已非常接近，但受中心射流作用无法聚并，二者各自的尾流使气泡发生远离，呈现出类八字形。取靠近过程的流场矢量图分析并行含尘双气泡上升过程中的流场变化，结果如图15 所示。由图15 可知，当两气泡靠近时，靠近部分流场的挤压作用可能更有利于颗粒向气液界面运动；相比于含尘单气泡，并行含尘双气泡周围的多个涡旋强化了颗粒的脱除。

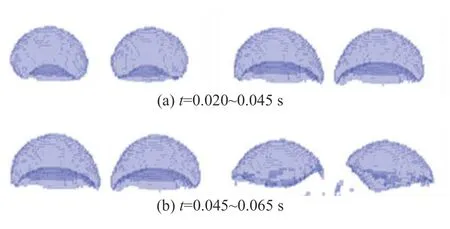
图14 不同时段内并行含尘双气泡运动趋势变化(db=8 mm)Fig. 14 Trend change of parallel dust-containing double bubbles movement during different periods(db=8 mm)

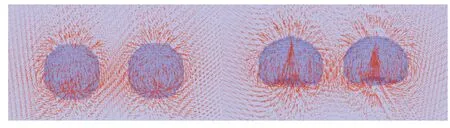
图15 并行含尘双气泡上升过程中流场变化(db=8 mm)Fig. 15 Flow field changes during the rising process of parallel dust-containing double bubbles(db=8 mm)

12 mm 与14 mm 的并行含尘双气泡也经历了靠近过程，但总体颗粒脱除率却下降，该现象可从两气泡相互作用导致双气泡的形变与含尘单气泡不同进行解释。由图5 可知，当气泡尺寸较大(12 mm与14 mm)时，两气泡靠近会使靠近侧被挤压变形，与含尘单气泡的对称变形及小尺寸并行含尘双气泡的对称变形不同，内侧所含空泡体积减小。由前文分析可知，脱除强化的机制在于靠近侧的流场挤压作用，但当受挤压侧变形空泡体积减小后，颗粒会更集中到两气泡的外侧区域，内侧颗粒浓度降低，如图16 所示，使得大尺寸并行含尘双气泡中颗粒的脱除率下降。

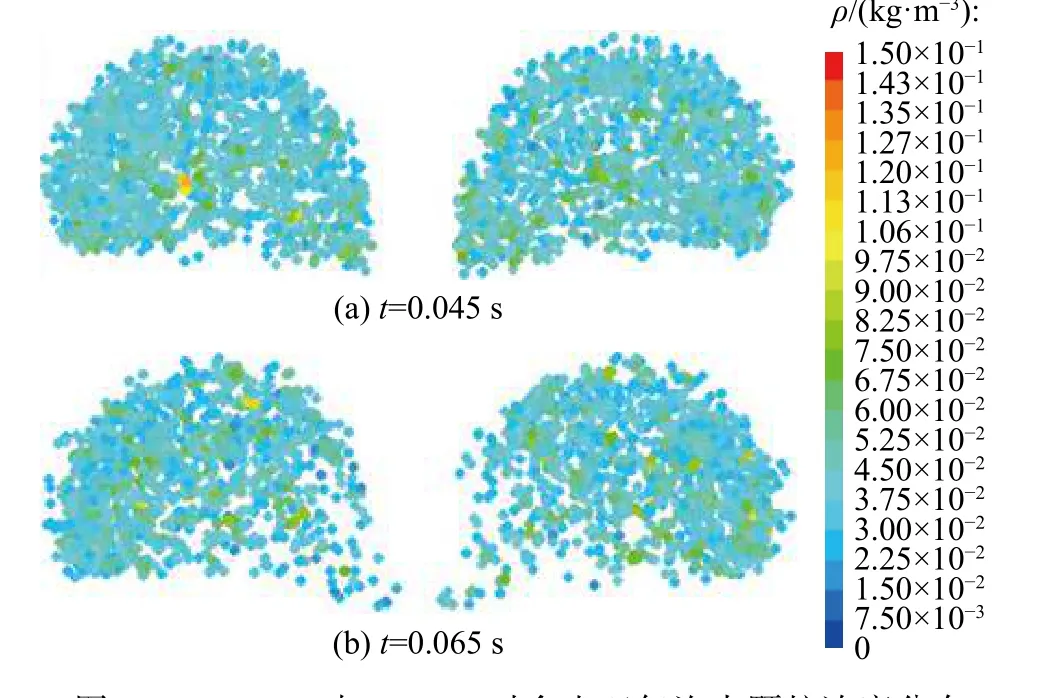
图16 t=0.045 s 与0.065 s 时含尘双气泡内颗粒浓度分布(db=12 mm)Fig. 16 Particle concentration distribution in dust-containing double bubbles at t=0.045 s and 0.065 s(db=12 mm)

3 结 论

本文通过DPM-VOF 耦合方法模拟研究了不同尺寸含尘单气泡和并行含尘双气泡在初始静止液体中的上升过程，以及对不同粒径颗粒脱除率的影响，得出结论如下：

(1) 当单气泡尺寸为6～14 mm 时，上升气泡的变形对颗粒的脱除具有增强作用，形变最复杂的6 mm气泡中颗粒的脱除率最高。

(2) 不同粒径的颗粒中存在能够使颗粒被高效脱除的适宜的气泡尺寸范围，1.0 μm 颗粒在6 mm 单气泡中表现出最佳的脱除率，2.5 μm 颗粒在8 mm 单气泡中脱除率最佳。

(3) 并行含尘双气泡的初始间距一定时，气泡在初始静止液体中的上升过程呈现“靠近-分离-靠近”的循环；受气泡间相互作用影响，并行含尘大气泡上升过程的形变与含尘单气泡不同。

(4) 不同尺寸并行双气泡上升过程中的相互作用对颗粒脱除的影响存在差异，8～10 mm 双气泡的相互作用强化了粒径为1.0 μm 颗粒的脱除，而12～14 mm 双气泡相互作用则弱化了粒径为1.0 μm 颗粒的脱除。