基于HVCE-RBFNN的矿区地表三维形变监测研究
周文韬 张文君 缪骏懿 申 锐 訾应昆
1 西南科技大学环境与资源学院,四川省绵阳市青龙大道中段59号,621010 2 国家遥感中心绵阳科技城分部,四川省绵阳市青龙大道中段59号,621010 3 四川航遥智测科技有限公司,四川省绵阳市涪金路389号,621010
随着测绘技术的不断更新,矿区地表形变监测方法取得了很大进展[1-2]。传统GNSS测量方法可得到高精度的单点三维形变数据,但仅依靠单点测量无法客观反映地表真实形变情况[3]。合成孔径雷达干涉测量(InSAR)技术具有高空间分辨率、高自动化和广域监测等优点,为形变监测领域提供了前所未有的机遇[4-5]。然而,InSAR仅能监测沿卫星视距方向的形变,且由于合成孔径雷达(SAR)卫星近南北向飞行,导致其对南北向形变不敏感[6]。将GNSS与InSAR数据融合解算三维形变场是目前国内外众多学者关注和研究的热点[7-9]。目前的融合方法主要分为2种:1)将GNSS南北向形变插值后代入解算InSAR在东西向和垂直向的形变场[10],但该方法过于依赖GNSS在南北向的形变精度,忽略了InSAR在南北向形变的贡献;2)通过建立合适的融合模型解算三维形变场[11],但会遇到先验方差不准确及迭代负方差的情况,导致不能完整地表达真实地表三维变化。
本文以金昌市金川西二采矿区为研究对象,提出一种融合赫尔默特方差分量估计(Helmert variance component estimation, HVCE)和径向基函数神经网络(radial basis function neural network, RBFNN)的三维形变计算法HVCE-RBFNN。利用该方法对同期的GNSS和InSAR数据进行迭代定权,解算出地表三维形变场,并与地下采空区进行对比分析,以期为矿区地表三维形变监测提供新方法。
1 HVCE-RBFNN模型建立
1.1 InSAR三维几何分解原理
传统InSAR技术仅能获取沿卫星视线(LOS)向的一维形变,然而真实地表形变通常是三维的,因此需要将InSAR单一方向的形变分解为三维方向的形变。根据卫星侧视观测几何,沿卫星LOS向的形变可分解为地表某一点在东西向、南北向和垂直向的位移[12],如图1所示。InSAR的累积形变DLOS可以表示为:

图1 InSAR三维几何分解原理Fig.1 3D geometric decomposition schematic of InSAR
DLOS=-DEsinθcosα+DNsinθsinα+DUcosθ
(1)
式中,DE、DN和DU分别为地面点P沿东西向、南北向和垂直向的位移;θ为卫星入射角;α为卫星方位角,以顺时针方向为正。令S=[SESNSU]T、SE=-sinθcosα、SN=sinθsinα、SU=cosθ分别为卫星LOS向形变在三维方向的投影。
1.2 HVCE-RBFNN模型
假设有n组观测数据,且各组数据之间互不相关,根据间接平差的数学模型有:
Vi=Bi-li,i=1,2,…,n
(2)
式中,Vi为改正数矢量;Bi为系数矩阵;li为观测数据。法方程表达式为:
=N-1W
(3)
式中,Pi为权重矩阵,在第1次最小二乘平差中可定义为任意矩阵[13]。
通常情况下,由于很难准确计算观测数据的先验方差,因此在第1次平差中给定的权阵Pi也是不合理的。为此引入HVCE法,设各组观测数据的单位权方差为,则有:
=A-1Wθ
(6)
式中,ai为各组观测数据li的观测量个数。根据式(7)计算新的权重矩阵为:
式中,c为任意常数。将求得的新权阵i代入式(2)中计算,直至满足:
当满足式(11)时,可输出计算结果。各类观测数据差异较大时,往往会导致式(11)出现负方差的情况,这是因为观测方程系数矩阵秩亏,导致矩阵N病态或完全秩亏,使得N-1→∞,N-1与法矩阵Ni的乘积的迹tr(N-1Ni)→∞,从而导致迭代出现负方差。基于此,采用RBFNN算法对负方差的点进行计算。
RBFNN具有自主学习、自主组合和自主适应等特点,可对差异较大的数据进行训练,从而达到数据融合的目的,不仅解决了计算效率的问题,还可完整地表达各组数据在融合中的贡献[14]。RBFNN由3层前向网络构成,第1层为输入层,第2层为隐含层,第3层为输出层,其数学模型表示为:
(12)
式中,wij为权值;X为训练样本;xi为基函数中心;φ(‖X-xi‖2)为基函数;k为输出单元数。
RBF函数中心确定的方法不同,RBFNN的学习策略也不同。根据各组观测数据的特点,采用随机选取固定中心的学习策略,使基函数中心和标准差恒定不变。当各组数据比较典型、具有代表性时,这种策略的学习效率会大幅提升。传递函数选择高斯分布函数:
式中,r为模糊半径;σ为基函数的标准差。为防止RBF函数过尖或过平,对σ进行选取:
式中,dmax为选取中心之间的距离;n为隐含节点个数。得到基函数为:
i=1,2,…,n
(15)
最后采用伪逆法计算权值:
ωij=φ(‖X-xi‖2)dkj
(16)
式中,dkj为期望输出值。
2 实验分析
2.1 研究区概况及数据介绍
金川西二采矿区位于甘肃省金昌市(图2),地处河西走廊中段、祁连山北麓,平均海拔1 700 ~2 700 m。该区属大陆性温带干旱气候,光照充足,气候干燥,降水少且蒸发强,地下水系不发育,总体生态环境较弱[15]。矿区地下开采范围南北长420 m,东西宽230 m,总面积约43 512 m2。由于长期受地下开采和断层活动影响,矿区地表塌陷明显,安全隐患极大。

(a)矿区地理位置;(b)实验SAR影像覆盖情况;(c)监测点位分布;(d)地面监测桩图2 研究区概况Fig.2 Overview of the study area
本研究在地表均匀布设139个监测点,得到2019-04~2020-06期间GNSS三维形变数据。通过欧洲航天局官网下载同期67景C波段升降轨Sentinel-1A斜距单视复数(SLC)影像,卫星重访周期为12 d,分辨率为5 m×20 m,为提高数据处理效率,裁剪影像至合适区域(图2(b)),实验参数详见表1。

表1 Sentinel-1A实验参数Tab.1 The experimental parameters of Sentinel-1A
根据前文可知,受SAR卫星飞行轨道影响,InSAR在各方向的敏感程度不同。提取表1中卫星升降轨入射角和方位角,可由式(1)表示为:
由式(17)可知,InSAR数据对垂直向形变最敏感,东西向次之,南北向不敏感。
2.2 实验过程与分析
针对GNSS监测数据,采用克里金(Kriging)插值法将点数据内插至与InSAR相同像元的面,得到GNSS三维形变场(图3)。采用短基线集(SBAS)方法处理InSAR数据,并引入AUX_POEORB精密定轨星历和30 m分辨率的SRTM DEM数据去除地形相位,得到升降轨LOS向累积形变场(图4,其中东、北和上为正方向)。

图3 Kriging插值的GNSS三维形变场Fig.3 GNSS 3D deformation fields with Kriging interpolation

图4 升降轨InSAR LOS向形变场Fig.4 InSAR LOS direction deformation fields of ascending and descending
利用GNSS三维形变与InSAR升降轨LOS向形变结果提取融合后的三维形变场,根据式(2)构建误差方程:

为验证HVCE-RBFNN法的有效性,分别用3种方法进行解算:1)结合GNSS南北向形变与InSAR升降轨LOS向形变,解算东西向和垂直向形变场;2)结合GNSS三维形变与InSAR升降轨LOS向形变,采用等权估计法定权,利用最小二乘法解算融合后的东西向、南北向和垂直向形变场;3)采用HVCE-RBFNN法融合解算方法2中的5组形变数据的东西向、南北向和垂直向形变场。由方法1可以解算东西向和垂直向形变场,南北向形变场由GNSS插值代替,方法2和方法3可解算东西向、南北向和垂直向形变场。将139个监测点的观测量作为真值,分析3种方法三维形变的精度,结果如表2所示。

表2 不同方法的三维形变误差Tab.2 The 3D deformation errors of different methods
由表2可以看出,方法1南北向RMSE为0 mm,但东西向RMSE达到50.22 mm,垂直向RMSE达到75.63 mm,监测精度较低。对比方法1和方法2发现,方法2在综合考虑了GNSS三维形变和InSAR升降轨LOS向形变的情况下,东西向和垂直向的形变精度显著提升,南北向形变精度虽不及方法1,但顾及了InSAR监测在南北向的贡献,精度可达mm级。对比方法2和方法3发现,后者在三维方向的精度略优于前者,尽管二者的精度差别不大,但在一般情况下,方法2利用等权法决定权重难以将各组数据进行合理融合。综上,通过方法3迭代定权解算的三维形变结果精度优于方法1和方法2。
2.3 地表三维形变结果及分析
图5为139个监测点GNSS三维形变结果与方法3得到的结果的对比。不难发现,由于InSAR对垂直向形变最为敏感,对南北向形变最不敏感,因此图5(c)中融合形变较GNSS形变有一定差异,但曲线走势基本一致;图5(b)中2种形变曲线高度一致,验证了InSAR对南北向形变贡献小的问题;图5(a)中曲线走势介于图5(b)和图5(c)之间。整体来看,利用HVCE-RBFNN法得到的三维形变结果与GNSS三维形变结果较为一致。
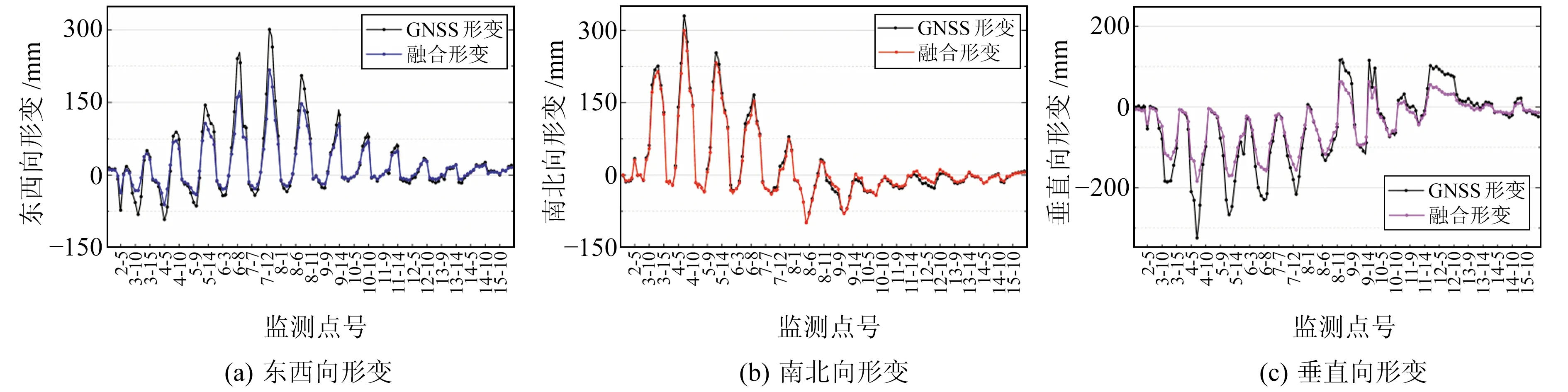
图5 GNSS与HVCE-RBFNN法的三维形变结果对比Fig.5 Comparison of 3D deformation results between GNSS and HVCE-RBFNN method
提取西二采矿区融合后的三维形变场,并与地下采空区位置进行叠加,以分析地下开采对地表的影响。由图6(a)可知,采空区以西区域向东偏移,最大偏移量为228 mm;采空区以东区域向西偏移,最大偏移量为62 mm。由图6(b)可知,采空区以南区域向北偏移,最大偏移量为300 mm;采空区以北区域向南偏移,最大偏移量为99 mm。由图6(c)可知,矿区最大沉降量为193 mm,最大抬升量64 mm,沉降中心与采空区中心重叠,在地表形成沉降盆地。
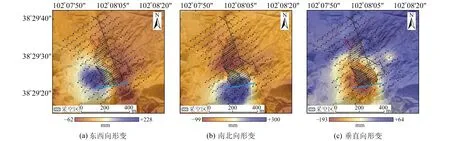
图6 基于HVCE-RBFNN法的三维形变场Fig.6 3D deformation fields based on HVCE-RBFNN method
采空区地表东西向和南北向的形变量在采空区中心表现平稳,并由中心向两侧先增大后减小,垂直向形变量由采空区中心向四周逐渐减小。整体来看,研究区地表形变受地下开采和断层影响,但其三维形变结果与采空区基本一致,符合开采沉陷规律。
3 结 语
本文以金昌市金川西二采矿区为研究对象,分别采用GNSS和SBAS-InSAR方法对矿区地表进行监测,得到GNSS在三维方向和升降轨InSAR在LOS向的形变数据;然后根据GNSS和InSAR的优势互补性提出HVCE-RBFNN方法解算矿区地表三维形变,并通过3种不同的融合方法验证其有效性。计算表明,本文方法解算的三维形变结果在东西向、南北向和垂直向的RMSE分别为20.85 mm、7.41 mm和34.47 mm,优于其他2种方法。同时,利用本文方法获取的三维形变场与采空区基本一致,符合开采沉陷的基本规律。由此可知,本文提出的方法可用于矿区地表的三维形变监测。

