GPT3模型反演GNSS大气可降水量精度评定

蔡 猛 刘立龙,2 黄良珂 莫智翔 黄东桂 李浩杰

1 桂林理工大学测绘地理信息学院，桂林市雁山街319号，541006 2 广西空间信息与测绘重点实验室，桂林市雁山街319号，541006

大气水汽是对流层的重要组成之一，其变化与降水直接相关。大气可降水量PWV是单位面积空气柱里含有的水汽总数量，通常用来反映对流层中大气水汽的分布和变化。传统的大气水汽探测方法主要包括无线电探空站、微波辐射计、雷达观测和卫星遥感等，但由于费用昂贵，且时空分辨率低，这些方法离监测和预报中小尺度灾害性天气的要求还有很大差距。地基GNSS能较好地弥补传统大气水汽探测在时空分辨率上的不足，并提供精细化气象预报所需要的高精度、近实时的大气水汽资料，已逐渐成为获取大气水汽的主要方法[1-6]。然而，使用地基GNSS反演大气水汽时需要获取地面气压和气温等气象数据，但大部分GNSS观测站未配备气象传感器。因此，本文探讨利用GPT系列模型的最新模型GPT3[7]提供的气象参数来反演PWV，并选用探空站资料验证该模型的有效性。

1 数据来源及计算方法

1.1 数据来源

探空站资料可提供每天00:00和12:00的实测地表及分层气象数据，数据可从美国怀俄明州立大学网站(http:∥weather.uwyo.edu/upperair/sounding.html)下载。中国大陆构造环境监测网络(CMONOC)提供的GNSS观测数据可通过中国地震局GNSS数据产品服务平台(http:∥www.cgps.ac.cn)获取。本文选用2017～2018年49个GNSS站和与其并址的探空站数据进行实验，站点位置见图1。

图1 GNSS站与探空站分布Fig.1 Distribution of GNSS stations and radiosonde stations

1.2 GNSS PWV反演计算

GPT3模型的表达式为：

式中，r(t)为模型估计的大地水准面处的气象参数函数；doy为年积日；A0为年平均振幅；A1、B1和A2、B2分别为年周期和半年周期参数。GPT3模型仅需输入测站位置和年积日即可输出气压、气温、Tm等气象参数。本文利用GPT3模型计算出49个探空站和49个GNSS站处的气压、气温和Tm。因探空站采用海拔高，GNSS站采用大地高，故使用EGM2008模型统一高程[8]。

首先利用GNSS观测数据解算对流层天顶总延迟量(ZTD)，再根据Saastamoinen模型[9]计算天顶静力延迟量(ZHD)，将其从天顶总延迟中减去，从而得到天顶湿延迟(ZWD)。最后利用ZWD与PWV转换系数K计算得到PWV：

PWV=K·ZWD

(2)

(3)

式中，ρw=1×103kg/m3为液态水的密度；Rv=461.495 J/(kg·K)为水汽气体常数；k′2、k3为大气物理参数，经验值通常为22.13±2.20 K/hPa、(3.739±0.012)×105K/hPa。采用Bevis经验公式Tm=70.2+0.72Ts计算Tm，其中，Ts为地表温度。

2 精度评估

采用偏差(bias)与均方根误差(RMSE)为评估指标，以12 h时间分辨率的探空站资料中的气压、气温和Tm数据为参考值，评估GPT3模型的气压、气温和Tm的精度：

(4)

(5)

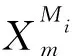
2.1 GPT3模型计算气温、气压的精度评估

用GPT3-1和GPT3-5分别表示1°和5°分辨率的GPT3模型，每个站上气压和气温的bias和RMSE见图2，bias和RMSE统计结果见表1、2。

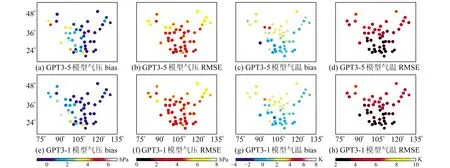
图2 利用探空站检验GPT3模型气压和气温的bias和RMSE分布Fig.2 Distribution of bias and RMSE values of air pressure and temperature obtained from GPT3 tested by radiosonde stations

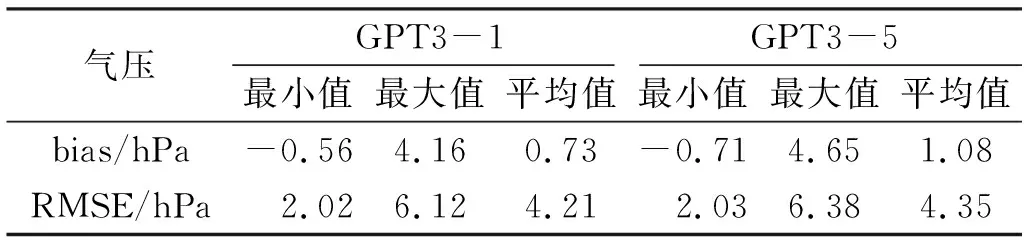
表1 气压精度统计Tab.1 Accuracy statistics of air pressure

由图2可知，GPT3-1和GPT3-5模型气压在中国西部出现较大bias的情况比其他地区多，并且在中国东北地区和西北地区均表现出较大的年均RMSE；GPT3-1和GPT3-5模型气温在中国西部地区不仅表现出较大bias，而且也表现出较大的年均RMSE，其原因可能是西部地区地形起伏较大。

由表1可知，GPT3-1模型的气压bias均值为0.73 hPa，最大值与最小值之差为4.72 hPa，气压RMSE均值为4.21 hPa，最大值与最小值之差为4.1 hPa；而GPT3-5模型的气压bias和RMSE均值比GPT3-1模型分别高0.35 hPa和0.14 hPa，说明GPT3-1模型的气压精度比GPT3-5模型更优。

由表2可知，GPT3-1模型的气温bias均值为1.34 K，最大值与最小值之差为5.32 K，气温RMSE均值为3.75 K，最大值与最小值之差为4.41 K；GPT3-5模型的气温bias和RMSE均值与GPT3-1模型接近。

表2 气温精度统计Tab.2 Accuracy statistics of temperature

表1、2说明，GPT3-1模型的气温和气压精度优于GPT3-5模型。

2.2 GPT3模型计算Tm的精度评估

同样采用中国地区2017～2018年49个与GNSS站并址的探空站提供的Tm作为参考值来评价GPT3模型Tm的精度，并统计GPT3模型Tm的bias和RMSE，结果见图3和表3。

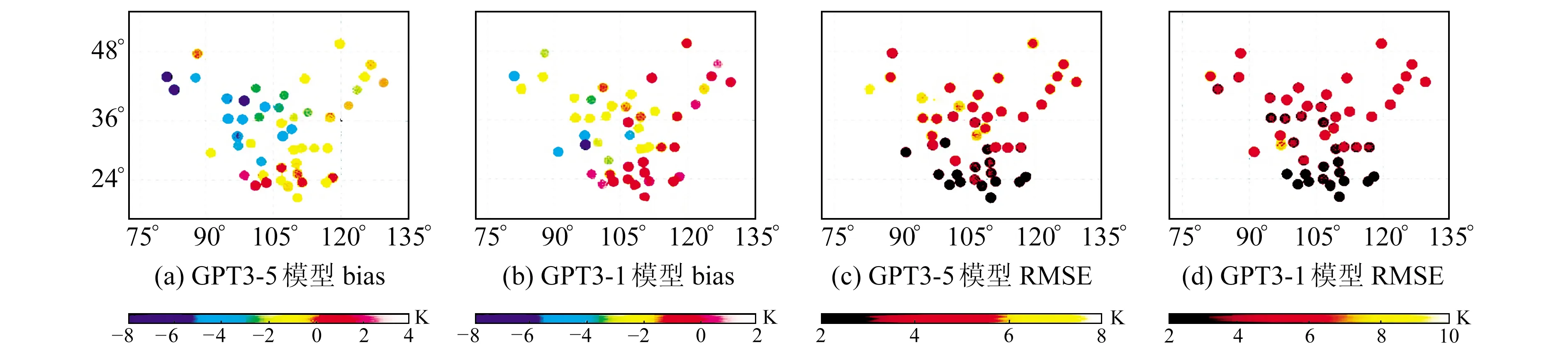
图3 利用探空站检验GPT3模型Tm的bias和RMSE分布Fig.3 Distribution of bias and RMSE values of Tm obtained from GPT3 model tested by radiosonde stations

表3 Tm精度统计Tab.3 Accuracy statistics of Tm

由图3可以看出，GPT3-1和GPT3-5模型高bias主要出现在中国西部地区，其他地区bias较小。2种模型在中国北部及西南地区的RMSE高于南部低纬度地区，其主要原因是西部地区地形起伏大、北部地区存在显著的Tm日均周期，而在南部低纬度地区和东南部地区，Tm的变化振幅低于中纬度地区，有利于对Tm进行精确模型化[10-11]。

由图3和表3可知，GPT3模型在中国区域表现出显著的负偏差，且主要集中于西部地区。说明GPT3模型估算的Tm值在多数西部地区测站上要低于探空站计算的Tm值。这是由于GPT3模型在计算Tm时没有考虑高程改正[3]，导致在地形起伏相对较大的西部地区产生显著的负偏差。GPT3-5和GPT3-1模型的bias均值分别为-1.91 K和-1.67 K，最大值分别为1.99 K和0.70 K，说明GPT3-1模型比GPT3-5模型更稳定；GPT3-5和GPT3-1模型的RMSE均值分别为4.39 K和4.15 K，也表明GPT3-1模型的性能要优于GPT3-5模型。

为了进一步分析2种模型Tm的精度，对49个站的bias和RMSE进行统计，结果见图4。

图4 Tm的bias和RMSE分布直方图Fig.4 Histogram of bias and RMSE of Tm

由图4可知，GPT3模型的2种分辨率均呈现出明显的负bias，其中GPT3-5模型的bias变化更为显著，说明GPT3-1模型比GPT3-5模型更稳定。同时，GPT3-1模型的RMSE分布要比GPT3-5模型集中，表明GPT3-1模型的性能要比GPT3-5模型好。

2.3 基于GPT3模型的GNSS反演PWV的精度分析

由上述分析可知，GPT3-1模型的精度和性能优于GPT3-5模型，因此下文选用GPT3-1模型来反演PWV并进行精度分析。

为分析不同区域基于GPT3-1模型2种方案(GPT3-1模型提供的气温结合Bevis经验公式计算得到Tm(Bevis-PWV)和GPT3-1模型提供的Tm(GPT3-PWV))反演的PWV与探空站利用实测地表温度反演的PWV(TKZ-PWV)的偏差，选取SXTY、HBES、SCGZ、XJKC等4个GNSS站(分别代表北方、南方、青藏、西北地区)2018年数据进行分析，结果见图5。图6为GPT3-1模型2种方案反演的PWV与探空站反演的PWV的差值时间序列(GPT3-TKZ表示利用GPT3模型Tm反演的PWV与探空站反演的PWV差值，GPT3B-TKZ表示采用GPT3模型提供的气温结合Bevis经验公式得到的Tm反演的PWV与探空站反演的PWV差值)。

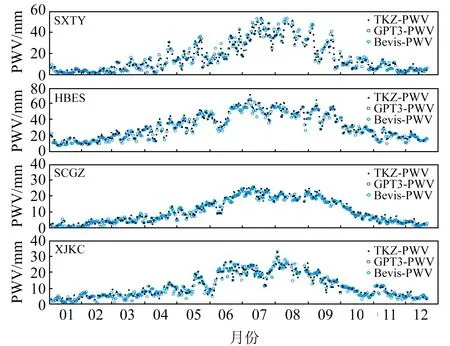
图5 SXTY、HBES、SCGZ和XJKC站PWV时间序列Fig.5 PWV time series at SXTY, HBES, SCGZ and XJKC stations

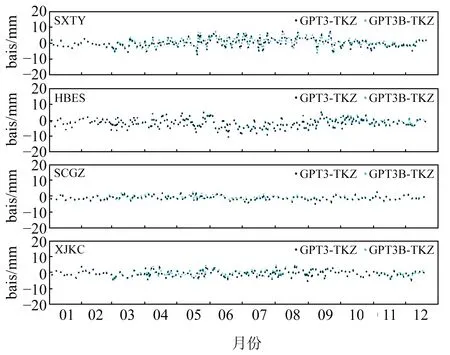
图6 SXTY、HBES、SCGZ和XJKC站GPT3模型反演的PWV与探空站反演的PWV的偏差Fig.6 Bias of PWV derived from radiosondes with respect to GPT3 model-derived PWV at SXTY, HBES, SCGZ and XJKC stations

由图5可知，Bevis-PWV、GPT3-PWV与TKZ-PWV的整体变化趋势基本吻合，具有很好的一致性，利用GPT3模型2种方法反演的PWV精度相当。由于我国夏季气候温暖湿润，PWV表现出明显的季节性变化，其峰值一般出现在6～9月。其中，HBES站位于我国南方，水汽含量大，因而其PWV明显高于其他3个站。由图6可知，除HBES站外，2种方法反演的PWV与探空站反演的PWV之间的差值主要集中在5 mm以内。同时，这些差值的时间序列也表现出与PWV相似的季节性变化，其峰值出现在6～9月，表明该时期水汽变化剧烈。另外，由于GNSS站和探空站的位置存在距离，差值之间会出现一些异常值。

图7为2018年与探空站并址的49个GNSS站利用2种方法反演出的PWV与探空站推导的PWV之间的RMSE。为便于比较，将中国区域分为4大地区(北方、南方、青藏、西北)，同一地区测站放在一起。由图7可知，在大多数站点，GPT3-PWV、Bevis-PWV与TKZ-PWV之间的RMSE接近且部分几乎相等，说明2种方法反演的PWV的精度相当。由于中国南方地区气候温暖湿润，位于南方地区的多数站点的RMSE大于3 mm；少数位于北方地区的测站存在RMSE大于3 mm的情况，主要是由于这些站靠近海边，水汽含量和变化较大。相比之下，青藏地区和西北地区由于海拔高、气候干燥，其RMSE低于3 mm。由表4可知，基于GPT3模型反演的PWV精度在青藏和西北地区优于南方和北方地区，但北方和南方地区多数站点也能满足气象学应用要求[12]。

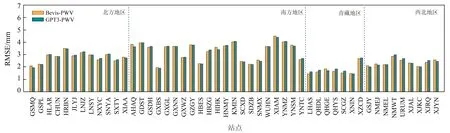
图7 基于GPT3模型反演出的PWV与探空站推导的PWV之间的RMSEFig.7 RMSE of GPT3 model-derived PWV with respect to radiosonde station-derived PWV

表4 中国不同地区PWV的RMSE统计Tab.4 RMSE statistics of PWV in different areas in China

3 结 语

本文利用中国地区2017～2018年49个与GNSS站并址的探空站数据对GPT3模型的气压、气温和Tm进行精度分析，并将GPT3模型提供的气象参数应用于GNSS水汽反演，结果表明：

1)与49个探空站实测的气压、气温相比，GPT3-1模型的气压和气温bias均值分别为0.73 hPa和1.34 K，RMSE均值分别为4.21 hPa和3.75 K；GPT3-5模型的气压和气温bias均值分别为1.08 hPa和1.31 K，RMSE均值分别为4.35 hPa和3.81 K。总体而言，GPT3-1和GPT3-5模型气温和气压在南方地区的精度优于北方地区和西部地区，并且GPT3-1模型优于GPT3-5模型。

2)GPT3-1模型Tm的精度和稳定性优于GPT3-5模型。相对于南方地区，GPT3模型估算的Tm在北方地区和西部地区表现出较大的误差，可能是受地形起伏大和显著的Tm日周期变化影响。

3)利用GPT3-1模型提供的气温结合Bevis经验公式得到的Tm反演的PWV和GPT3-1模型提供的Tm反演的PWV与探空站推导的PWV呈现出较好的一致性，且2种方法反演精度相当。总体而言，南方和北方地区站点反演的PWV的RMSE要大于青藏和西北地区，因而GPT3模型在青藏和西北地区反演大气水汽的精度更高，但北方和南方地区多数站点精度也能满足气象学应用要求。