基于 LOF 与 CEEMD 的城镇取用水监测数据异常值识别
宋丽娜 ,刘 淼 ,秦 韬 ,何 鑫 ,郭中磊 ,王小胜
(1.河北工程大学数理科学与工程学院,河北 邯郸 056038;2.河北省水资源研究与水利技术试验推广中心,河北 石家庄 050000;3.中国水利水电科学研究院水资源研究所,北京 100038)
0 引言
在我国北方缺水地区,为确保节约用水与水资源高效利用,对城镇取用水进行监测与管控十分必要。近年来,对城镇取用水户取用水的在线监测已成为国家水资源监控能力建设的一项重要内容。但由于取用水在线监测数据随机性强,易受环境与人为因素的影响,大部分监测数据极易受到异常值的干扰,若不经处理直接使用则难以客观真实地反映当地取用水的实际情况,并且由于水资源监控数据规模日益增大,依靠人工检测异常值存在难度。因此,研究开发能够有效识别城镇取用水监测数据中异常值的科学方法,对后续用水总量管控和水资源税征收等工作具有重要意义。
有效识别数据集中的异常值是数据分析中十分重要的环节。取用水监测数据中的异常值识别是一个新兴的研究课题,目前行业对于识别方法尚未形成共识,同时学术界对于异常值的定义也没有统一标准。本研究定义的城镇取用水监测异常数据为某一时刻的数据与其邻域点相比出现偏离程度较大的数据。目前异常值识别方法可分为基于统计[1]、分类[2]、距离[3]等的方法。侍建国等[4]、刘明等[5]分别使用高斯分布的 3σ准则法与方差分析法对异常值进行识别,此类基于统计的方法存在数据无法简单服从某一特定统计分布条件的局限性。近年来,随着数据挖掘与人工智能技术的高速发展,基于人工智能的识别算法得到了广泛应用[6],魏晶茹等[7]、赵臣啸等[8]31分别将改进的支持向量机与孤立森林等算法应用到监测数据异常值识别中。这 2 种方法本质上是基于分类的异常值检测方法,适合小规模训练样本,在大规模数据噪声较多的情况下会导致分类性能下降。吴琼等[9]、林之岸等[10]、李航[11]分别将局部异常因子(LOF)算法应用于绝对重力测量与用电等数据异常检测方面,LOF 算法是一种基于距离的异常值识别方法,以上研究在使用 LOF 算法进行异常值检测时均取得较好的效果。由于取用水监测异常数据特征多样且复杂,单一的识别方法会受异常程度大的数据的影响而导致识别效果不佳,故有学者提出 2 种方法相结合分步识别的方法。方海泉等[12][13]258、杨瑛娟等[14]、张峰等[15]317基于统计的方法与集成经验模态分解(EEMD)相结合应用于水资源监测异常数据识别,验证了 EEMD 方法在取用水异常值识别方面的可操作性,且相比于传统单一的方法具有更好的适用性,识别效果也明显提高,但仍存在基于统计的方法依赖数据集分布的缺点,以及使用 EEMD 拟合数据有噪声残余的问题。
CEEMD(互补集成经验模态分解)法[16]是在传统经验模态分解(EMD)法[17]与 EEMD 法[18]上做出的改进,解决了 EMD的模态混叠与 EEMD 的噪声残余问题。因此针对城镇取用水监测数据体量大、类型多的特点,结合数据的可直观与不可直观识别异常值的情况,提出 LOF[19]93与 CEEMD 相结合的方法,分两步对城镇取用水监测数据异常值进行自动识别。
1 研究方法
1.1 LOF 算法
LOF 算法通过比较给定数据点与相邻点的密度判断数据是否异常,并同时量化出数据点的异常程度,具有识别速度快,精度高等特点[19]101。相关概念如下:
1)可达距离dk(P,O)。计算公式为
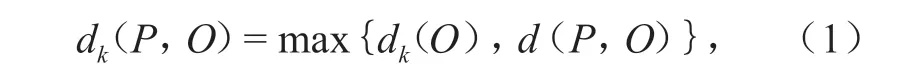
式中:dk(O)为点O的第k距离,即点O与距点O最近的第k个点之间的距离;d(P,O)是点O与点P之间的距离。
2)点P的局部可达密度ρk(P)。计算公式为
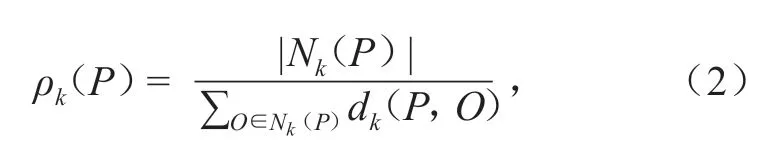
式中:Nk(P)为所有距离不大于dk(P)的点集合;|Nk(P)|为集合Nk(P)中点的个数。
局部异常因子lk(P)表示Nk(P)中其他点的局部可达密度与点P的局部可达密度之比的平均值,计算公式为
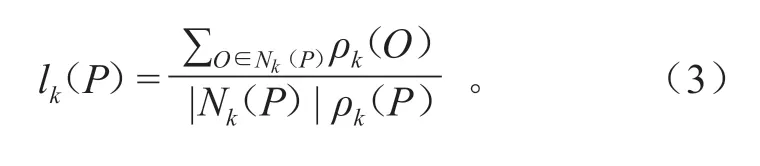
局部异常因子反映的是点P与其相邻点之间的离群程度。若lk(P)的值趋近于 1,说明点P与该点相邻点局部密度相近;若lk(P)的值大于 1,值越大则表示点P与相邻点越疏远,可视为可能的异常点。故可通过计算lk(P)判断数据集中任意点P的离群程度。
1.2 CEEMD 法
CEEMD 法在达到很好分解效果的同时,能够有效提高分解效率。序列经过 EMD 分解可以得到一系列高频到低频的固有模态函数(IMF)分量和1 个残余分量,其中:IMF 分量是接近单分量信号特征的 1 组函数,在每一时刻有且只有 1 个频率与之对应;残余分量通常不含有序列的振荡模态,只反映序列的变化趋势。CEEMD 法的分解步骤如下:
1)将时间序列数据x(t)(t为监测数据对应的时间)分别加上和减去正态分布的白噪声ui(t)构成 2 个新的序列,重复n次,则第i次序列为
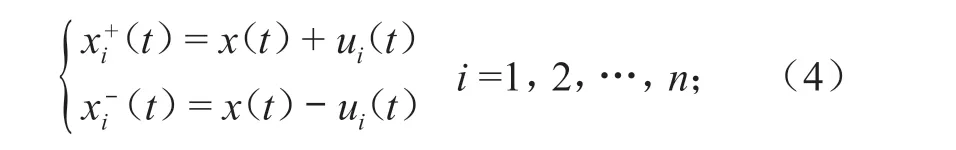
2)对每次构造的 2 个新数据分别用 EMD 进行计算,每组结果的总体平均分别记为和

4)对Ii求集总平均,即

式中:I为x(t)经过 CEEMD 分解得到的 1 组 IMF分量与 1 个残余分量。
2 异常值识别与修正方法
2.1 异常值识别模型
通过对城镇取用水户监测数据的统计分析,发现其异常数据具有多样性、复杂性等特点。按识别的难易程度,分为可直观与不可直观 2 种识别。可直观识别的异常值通常可以通过观察监测数据时间序列曲线的走向与变化得知,即缺失值、0 值、连续 0 值、突变幅度过大值;不可直观识别的异常值一般突变幅度不明显,是取用水量监测数据处理中的难点。
因此,针对城镇取用水量数据中同时存在可直观与不可直观识别异常值的特点,采取结合 LOF 与 CEEMD 组合模型的方法进行识别。首先,应用 LOF 方法对原始时间序列中的可直观识别异常值进行识别处理,即初识别阶段;其次,对修正后的序列进行 CEEMD 分解,将分解的低频分量叠加作为正常数据的参考序列,通过计算初识别后序列与参考序列之间的相对误差,进一步识别出不可直观识别异常值,即精识别阶段。分 2 步对异常值进行识别处理,可以降低不可直观识别异常值的漏检率与误检率,更好地提高监测数据的可靠性。模型结构如图 1 所示。
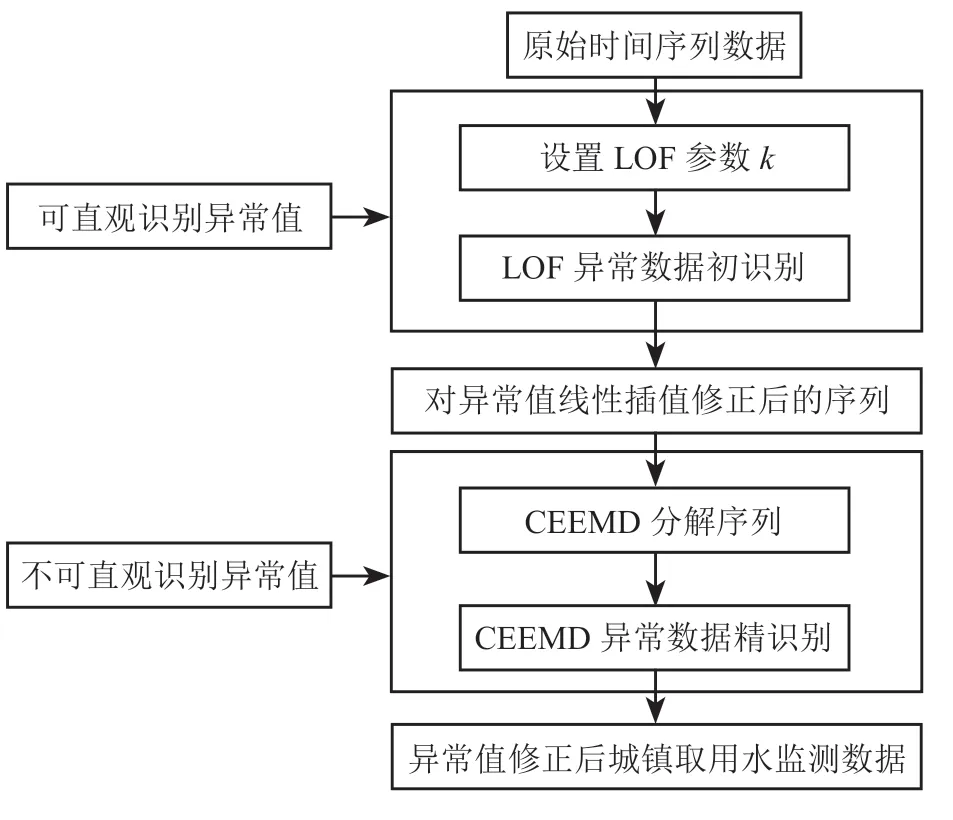
图1 异常值识别模型
2.2 异常值识别
2.2.1 LOF 初识别阶段
记原始日取水监测数据为x(t)。为避免缺失值、0 值、连续 0 值 3 类异常值对初识别的影响,先将其替换为空值,再利用 LOF 识别突变幅度过大的异常值。选定参数k后,计算各数据对应的 LOF 值lk(P),P=1,2,…,t。若lk(P)> 1,认为该点为异常数据点,lk(P)值越大,该点的离群程度越大,异常的可能性就越大。将识别到的异常值替换为空值并进行修正,其余数据顺序不变,记为x′(t)。
2.2.2 CEEMD 精识别阶段
初识别后的数据x′(t)是非平稳非线性的时间序列数据,对于序列中不可直观识别的突变幅度不明显的异常值,采用 CEEMD 方法进行分解,可得到尺度各不相同的N个 IMF 分量。将各分量按对应频率从高到低进行排序,并将后L个低频分量进行求和得到一个新的序列y(t)。当低频分量选取恰当时,低频分量叠加的序列既能滤除原始序列中的噪声影响,又能很好地保持序列中的趋势部分,即该叠加序列既能很好接近序列中的正常值,又不受异常值影响。根据经验,低频分量选取的个数L与 IMF 分量个数N的比例为 2∶3 时较合适[13]259,即。利用低频分量叠加后序列这一特点,将叠加序列y(t)与序列x′(t)进行对比,计算 2 个序列的相对误差δ,即
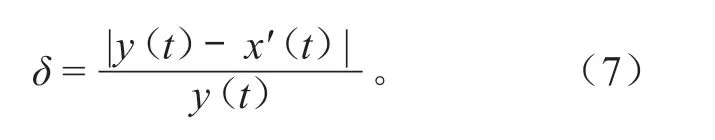
相对误差δ量化了数据之间的偏离程度,δ越大,偏离程度越大,异常的可能性越大。设置δ0为δ的阈值,当δ > δ0时,认为该点为异常数据点。将精识别后找到的异常值再次替换为空值并修正,记为x′(t)。
2.3 异常值修正
取用水监测数据是时间序列数据,对于识别出的异常值不能简单地进行剔除或做置零处理,这不仅会影响时间序列数据间的联系,也会影响后续数据分析与预测的质量。因此,对可直观与不可直观识别异常值分别采用线性插值与低频分量叠加数据进行修正,该方法在允许一定的误差下,可以对异常数据进行合理补偿,保证时间序列数据的连续性。处理方式如下:
1)可直观识别异常值。若ti是异常值点,x(ti)是其对应的异常值,x(ti-1)与x(ti+1)分别为异常值前后 2 个数据,则修正后的数据为
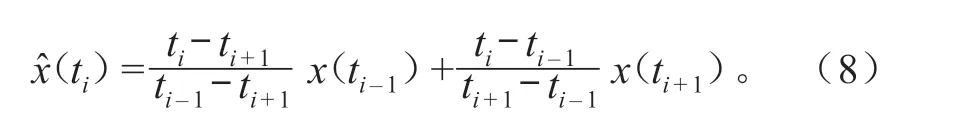
2)不可直观识别异常值。由于低频分量叠加后的序列能够很好地接近序列中的正常值,因此在精识别阶段,利用叠加后的序列对异常值进行修正。若ti是异常值点,x(ti)是其对应的异常值,y(ti)是点ti对应的低频叠加数据,则。
3 实验分析
3.1 实验目的
为验证 LOF 与 CEEMD 相结合的方法在识别城镇取用水监测数据异常值中的有效性,以河北省某自来水厂的取用水监测数据为例开展实验分析。首先,收集水厂取水口监测数据;其次,应用本研究方法识别异常值,对数据集中的异常值进行修正;最后,比较修正前后的取用水总量的变化,分析异常值分布规律。
3.2 实验数据
选取自来水厂 2019年日取水监测数据作为研究对象,共计 365 个数据点,具体监测数据如图 2 所示,记原始日取水量监测数据为x(t),数据来源于河北省水资源税取用水信息管理系统。该水厂位于河北省邯郸市,所用水源为浅层地下水,供水对象为水厂周围城镇居民生活用水,供水规律呈现出夏季多冬季少、白天多夜晚少的典型居民生活用水特征。从数据中可以看出,该水厂监测数据没有缺失数据、0 值与连续 0 值,存在突变幅度过大的异常数据,包括过大值与过小值,以过大值为主。
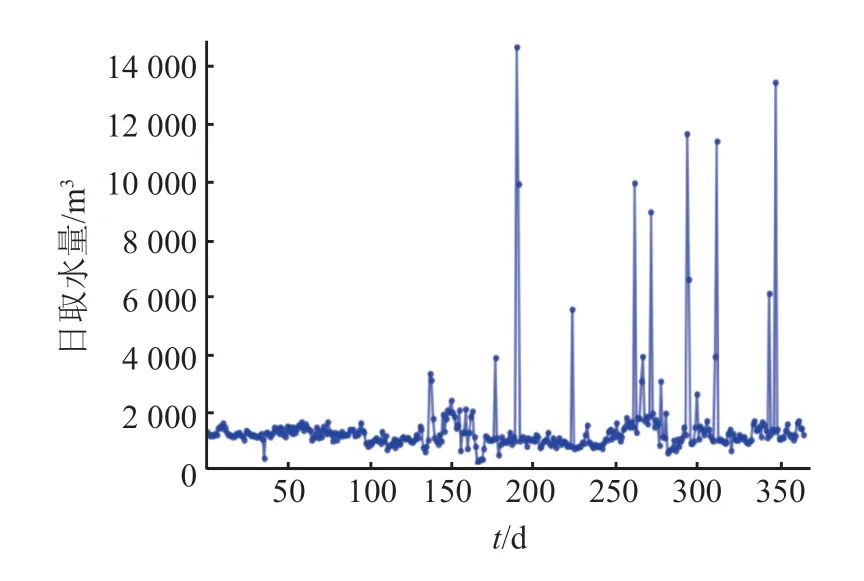
图2 原始日取水量监测数据
3.3 实验方法
3.3.1 基于 LOF 的可直观识别异常值初识别
取 3 组样本数据,选取k= 10,20,30 多种情况,进行异常值识别计算,识别效果如图 3 所示,图中A为可直观异常值个数,B为不同k值下检验出的异常值个数。
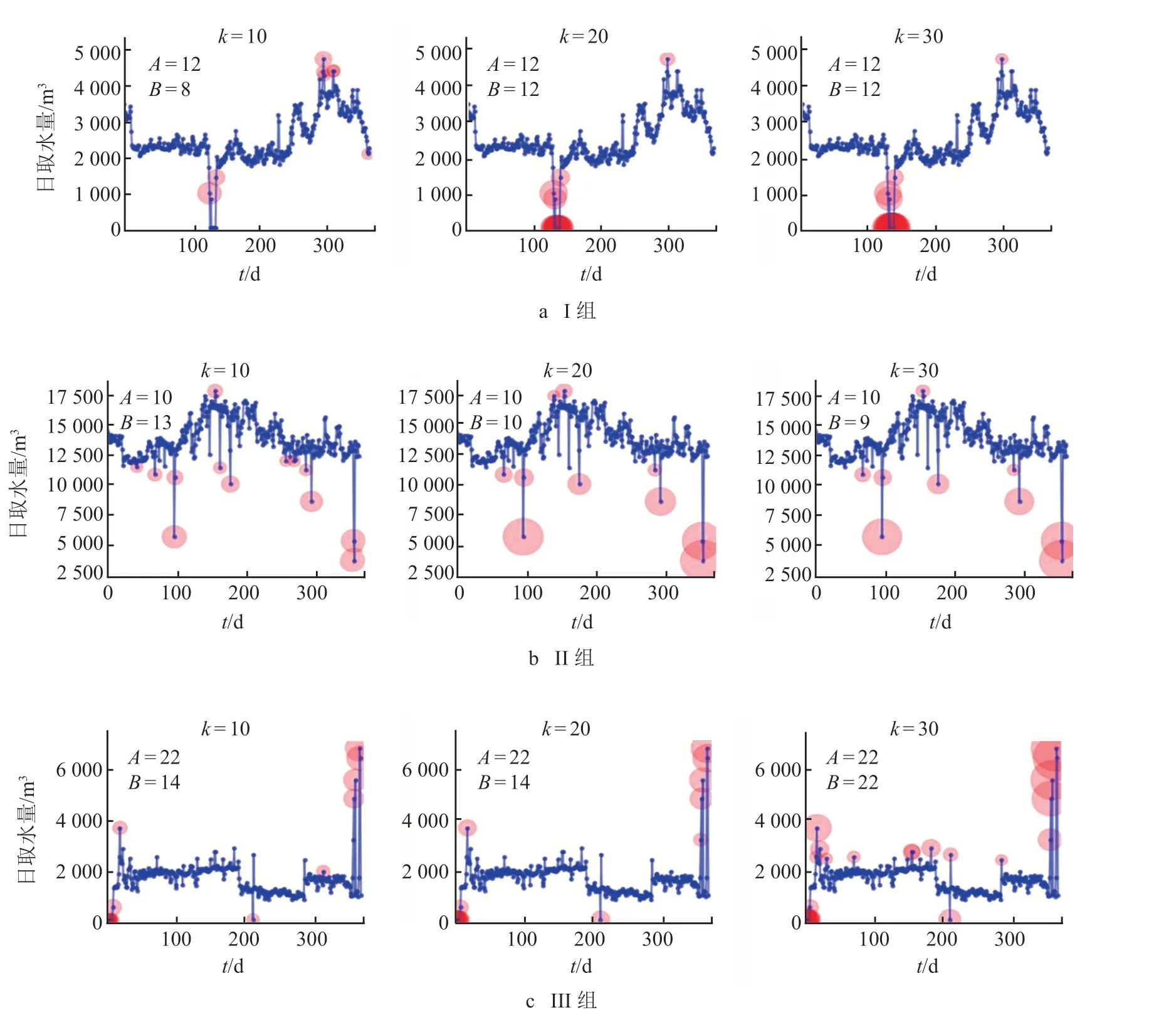
图3 不同 k 值下 3 组样本数据的识别效果
I 组共有 12 个异常点,当k= 10,20,30 时,可分别识别出 8,12,12 个异常值;II 组共有 10 个异常点,当k= 10,20,30 时,可分别识别出 13,10,9 个异常值;III 组共有 22 个异常点,当k=10,20,30 时,可分别识别出 14,14,22 个异常值。k=10 时,I 与 III 组数据中部分可直观异常值被漏检;k= 20 时,I 与 II 组数据识别效果明显有所提升,但 III 组数据仍有部分异常数据存在漏选情况;k= 30 时,3 组数据均能识别出可直观异常值,效果较好。
进一步将k的取值细分到 1~100,并对更多组样本数据进行异常值效果验证,发现:所研究的水厂取用水监测数据样本,当k≥ 30 时,能对样本有较好的异常值识别效果,考虑到k越大计算成本越高,耗时越大,因此本研究设定k= 30。
应用 LOF 进行可直观识别异常数据的初识别。设置k= 30,对序列x(t)初识别出突变幅度明显的 23 个数据点如图 4 所示,图中红色范围对应的是局部异常因子值的大小,面积越大说明 LOF 值越大,异常的可能性越大。从图中可以看出:LOF 在识别突变幅度较大的可直观异常值中的表现优异,不论是单独的还是连续的异常值都能被有效识别。同时 LOF 值的大小量化了异常点的异常程度,增加了异常数据在管理系统中的可视化水平,为人工判断异常值提供了更多参考。
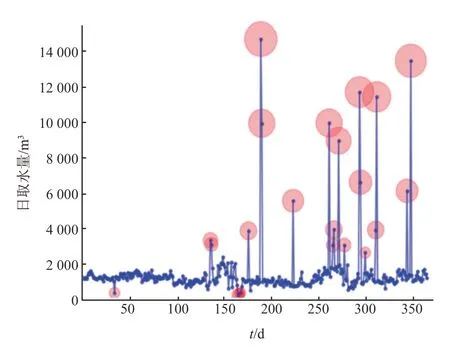
图4 基于 LOF 初识别的异常点(k = 30)
3.3.2 基于 CEEMD 的非可直观识别异常数据精识别
对时间序列x′(t)进行 CEEMD 分解,从高频到低频共得到 7 个分量,包括 6 个 IMF 分量与 1 个残余分量,如图 5 所示。
从图 5 可以看出:序列低频部分(IMF3~6,残余分量)可以刻画序列趋势,同时又蕴含着一定的周期波动成分;序列高频部分(IMF1~2)表现较为平稳,随机波动性较强,可视为噪声成分。去掉前 2 个高频分量,即滤除波动幅度大的噪声成分,再将后 5 个低频分量叠加,得到的序列y(t)如图 6 中红色虚线所示,图中蓝色实线为时间序列x′(t)。
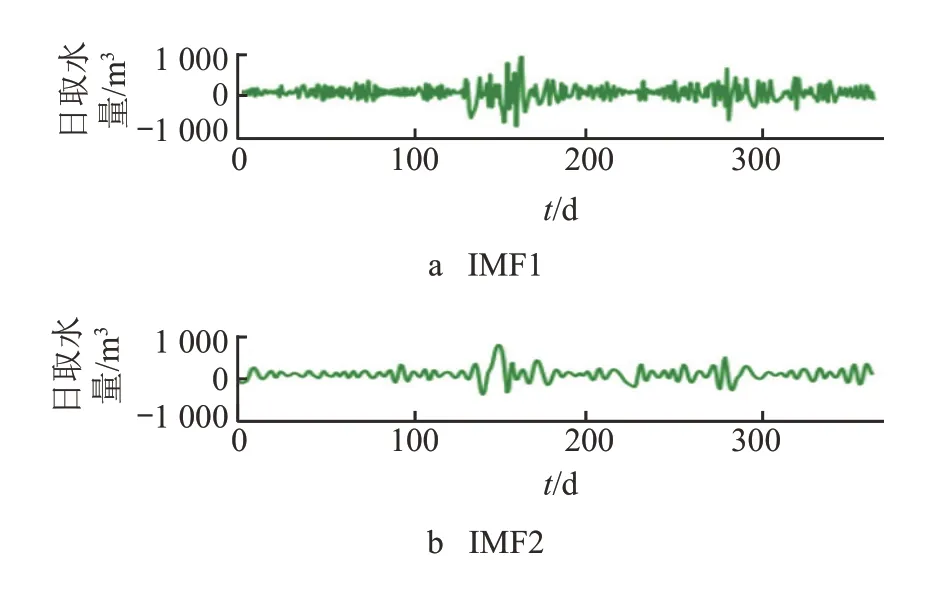
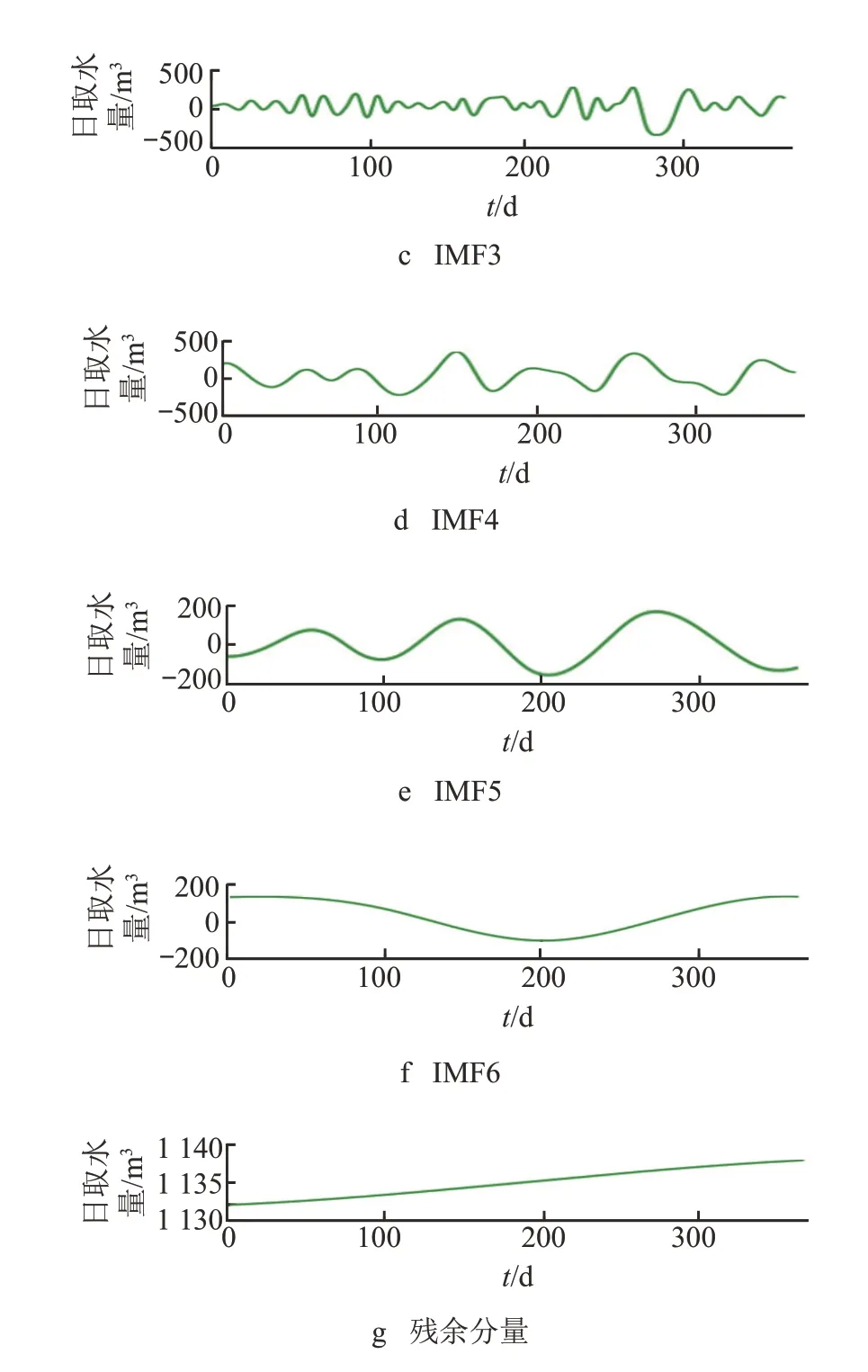
图5 初识别后的数据频谱 CEEMD 分解
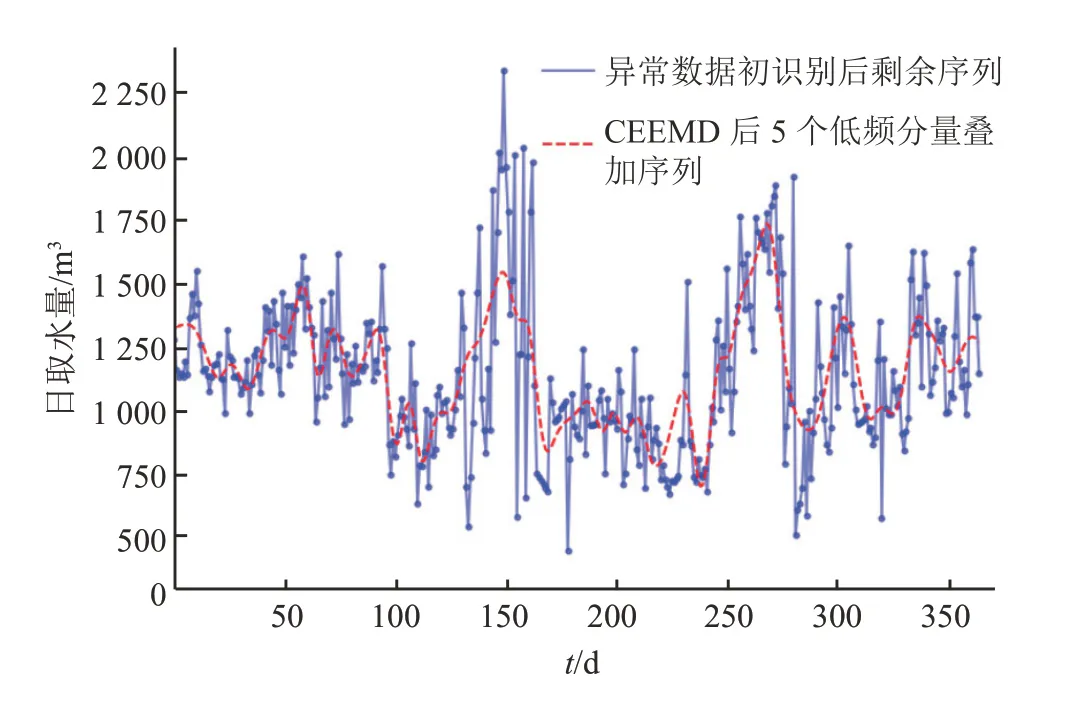
图6 低频分量叠加的拟合序列
根据式(7)计算 2 个序列之间的相对误差,结果如图 7 所示。结合现有统计数据及专家经验进行定量与定性分析,取 2 个序列相对误差δ的阈值δ0为 0.5,即当 2 条曲线对应的某点相对误差大于 0.5 时,判定该点为异常数据点[15]320。据此,经过 CEEMD 的分解与相对误差的识别,在异常数据精识别阶段共识别出 8 个异常数据,如图 8 所示。
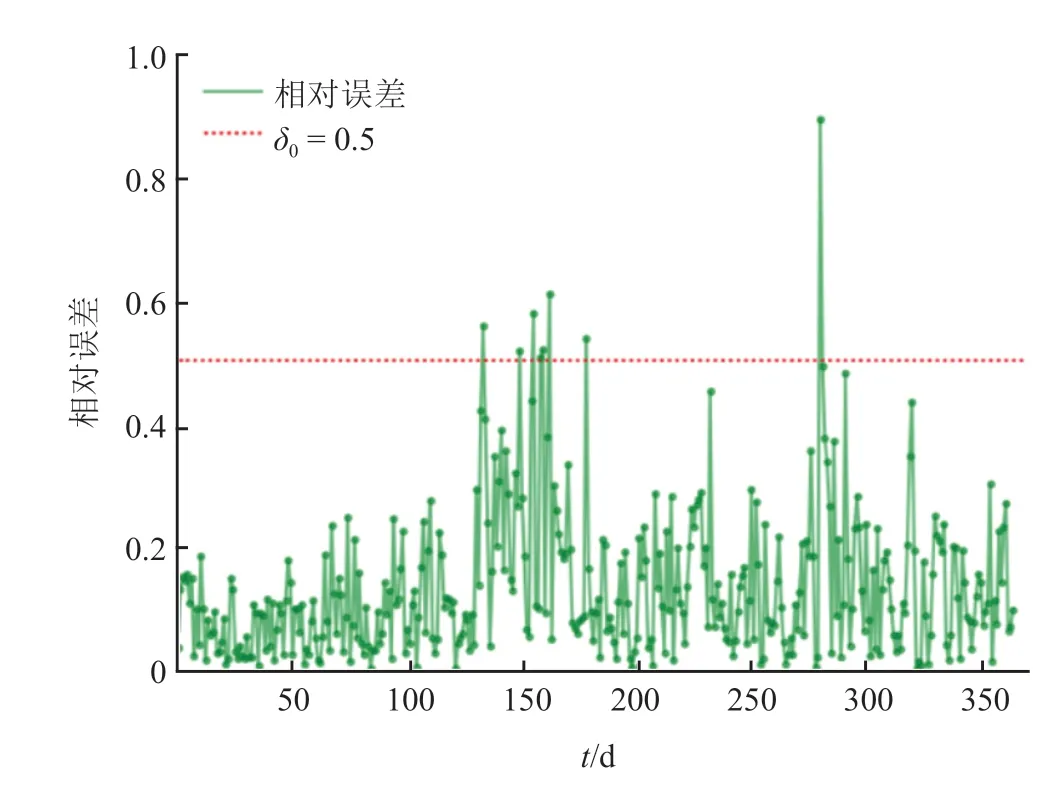
图7 相对误差
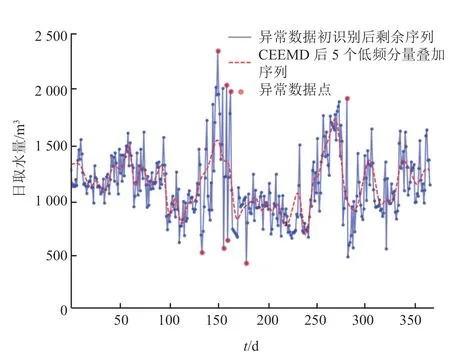
图8 基于 CEEMD 精识别的异常点
3.4 实验结果与分析
本研究共收集到河北省某自来水厂 1 个自然年内的取用水监测数据 365 个,取用水量共计51.27 万 m3。初识别阶段共找到异常数据点 23 个,利用线性插值进行初步修正后,得到的年度取用水量为 41.19 万 m3,变化幅度为 19.6%。精识别后又找到异常数据点 8 个,将其替换为低频分量叠加数据,最终取用水量修正为 41.14 万 m3,较初识别阶段变化幅度为 0.12%。通过观察案例识别的取用水监测数据异常值,发现异常值多集中在 8—10月,正是 1 a 中取用水量偏高的时间段,同时监测数据也呈现相同趋势,即夏季取用水量较其余时间取用水量更多。可以发现,取用水量偏高时出现异常值的概率会增大,主要原因是水资源监控能力建设的前期监控体系不完善,尤其是基础计量设施的选取与安装不太合适,因此在大规模建设监控网络的同时要加强监控设备的安装设计,以保障监测数据效力的发挥。
此外,对异常值进行识别的首要目的是监控取用水总量,因此为进一步说明取用水监测数据修正后的有效性,本研究利用 LOF 与 CEEMD 修正后的年取用水量数据与自来水厂核定的年取用水量数据进行比较。研究的自来水厂 2019年的核定年取水量为 34.42 万 m3,其中,核定取水量是当地水利部门根据原始实测数据,通过人工排查去除异常值并结合经验判别核定后的结果。由本研究可知,若使用未经质量控制的原始数据,则 2019年度该水厂的取用水总量为 51.27 万 m3,大于核定取水量与本研究计算的修正后取水量(41.14 万 m3)。这说明原始数据中存在测量过大的异常点占多数,本研究方法可以识别这些过大的异常点,具有一定的可靠性。本研究修正后的取水量仍大于核定取水量 6.72 万 m3,由于人工核定采用的方法标准不统一,因此无法断定人工核定的结果就一定比自动识别的结果更加准确。从分析对比中可以得出,自动识别异常点的修正是有效果的,且效率远高于人工筛选。
4 结语
城镇取用水户在线监测异常数据具有缺失值、0 值、连续 0 值,以及相比邻域点呈现突然上升或下降等特征。造成这些异常的原因有多种,包括监控设备故障或停用,数据传输过程失真,异常用水行为等,在本研究算例中,异常数据的存在形式主要以过大值为主。例如 2019年7月9日单日取用水量超过前一时刻 1.37 万 m3,与相邻数据规律明显不一致。这种情况极大概率是由监测设备损坏、数据传输异常等因素所致,较小可能是正常的用水行为。因此本研究方法可以给取水单位提供自动化的及时反馈,提示需要进行人工检查维修,对其设备异常、漏水与窃水等异常用水行为进行预警,与传统人工异常排查相比,工作量减少且排查效率更高。同时,本研究方法若应用于实践,可以避免后续统计取用水量时造成较大误差,为水资源的精准管理提供便利。
在异常值识别的方法方面,本研究采用初识别与精识别相结合的思路,结果证明:初识别可以有效地将绝大多数的异常点剔除,对用水总量的影响较大;精识别虽然对异常值的进一步过滤起到一定的作用,但是过程更为复杂,需要进行频谱分解,对总体用水量的影响很小。因此在计算条件不能充分允许的情况下,仅通过初识别就可以对数据集中的异常值形成较好的质量控制。
通过将修正后的年取用水量与自来水厂的核定数据进行对比,验证了顺序结合 LOF 与 CEEMD 的方法,结果具有一定的可靠性,可为进一步人工判断异常值提供一定支撑。尽管该方法在取用水异常值识别方面效果较好,但是对于异常值识别算法而言,不论基于何种数据特征的异常值识别方法,都只能找出可能异常值,并不能 100% 确定发生异常的原因[8]32,如在实际取用水过程中,观测数据会存在因实际用水行为突然发生变化而导致的观测值突变的情况,因此为准确判定是否为异常值,还需进一步结合专家经验进行判别。

