基于优化包覆层结构的高压单芯电缆暂态热路建模方法
曾含,王健,韩卓展,刘顺满,范星辉,聂阳阳,刘刚
(1.华南理工大学 电力学院,广东 广州 510641;2.广东电网有限责任公司广州供电局,广东 广州 510310)
随着用电量增大,电缆线路所需输送的电能也随之增加[1-2]。目前城市中广泛使用以XLPE材料作为绝缘的高压电缆[3-4],为了保证电缆绝缘在输送电能的过程中不会受到高温损伤[5-9],准确计算电缆的实时载流量十分重要。
目前,国外学者提出的电缆载流量计算方法主要有有限元法[10]、边界元法[11]以及热路法[12];国内学者提出的方法主要有无网格伽辽金法[13]和场路结合法[14-15]。其中,以有限元法和热路法最具有代表性。有限元法能够利用计算机软件,模拟电缆的运行环境,在各种复杂条件下进行计算;但其难以模拟持续多变的环境,在载流量实时预测中有所不足。传统热路法原理简单,但在构建热路模型时将电缆周围环境等效为单一均匀的介质,而电缆线路的敷设环境复杂多样,会造成较大的计算误差。为了解决电缆环境热参数难以确定的问题,刘毅刚等学者基于热电类比理论,提出一种由电缆表皮温度推算电缆线芯温度的热路解析法,该方法无需考虑外界环境的变化,对于掌握电缆的实时载流量和实时温度具有重要意义[16]。周凡、雷成华等学者在此基础上进一步优化热路模型,提出电缆动态增容等方法[17-19]。
有研究发现,采用传统热路模型通过电缆表皮温度计算电缆导体温度时,将电缆绝缘层集中处理,造成较大的计算误差,因此优化绝缘层暂态热路模型可以减小误差[20]。另一方面,传统热路模型将电缆包覆层中的绕包带、气隙层、皱纹铝护套划分为独立的串联结构,然后分层计算出各自的热容热阻参数。然而,刘刚等学者指出,皱纹铝护套与绕包带间的空气介质存在强制对流传热热阻,并且皱纹铝护套凹进部分与绕包带接触存在接触热阻[2]。由于电缆包覆层内部各层结构交错复杂、传热类型多样,不能将包覆层中的绕包带、气隙、皱纹铝护套视为独立结构串联建模。
为了进一步提高电缆暂态载流量计算精度,本文将绕包带、气隙层、皱纹铝护套合并为一层(包覆层),构建高压单芯电缆暂态热路模型。为了获取包覆层的热阻热容参数,首先进行第1次电缆暂态温升实验,基于实验得到的导体稳态温度和皱纹铝护套稳态温度,通过优化的暂态热路模型逆推出其热阻参数;采用逼近法求解热容参数,将基于给定初值并通过优化的暂态热路模型计算得到的导体温度与实验测得的导体温度进行比较,不断修正该值,使其满足精确度要求。然后在同类型电缆上进行第2次暂态温升实验,测量电缆表皮温升曲线以及导体温升曲线。利用第1次实验逆推的包覆层热参数和第2次实验测量的电缆表皮温升曲线,结合MATLAB、COMSOL软件,在优化建模假设下分别求取暂态热路法计算的导体温升曲线和仿真导体温升曲线。对比优化模型的导体温升曲线、传统模型的导体温升曲线与实验测量的导体温升曲线,验证将包覆层作为一层暂态热路模型的计算精度。
1 电缆暂态热路模型
1.1 电缆实际结构及参数
以YJLW0364/1101×500电缆为例说明电缆的实际结构与传统热路模型中的假设理想结构之间的差异。该电缆横截面如图1所示,纵截面如图2所示,电缆参数见表1[21]。
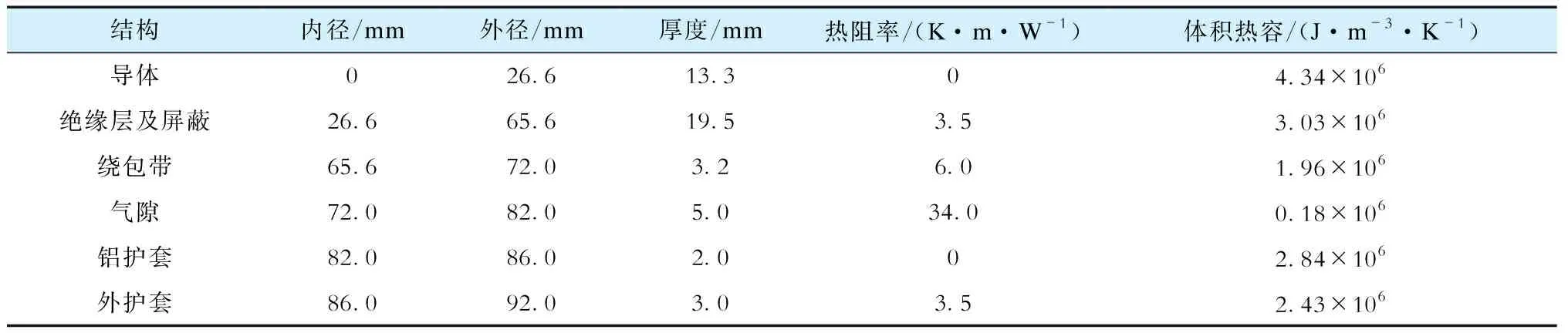
表1 YJLW0364/1101×500电缆参数Tab.1 YJLW0364/1101×500 cable parameters
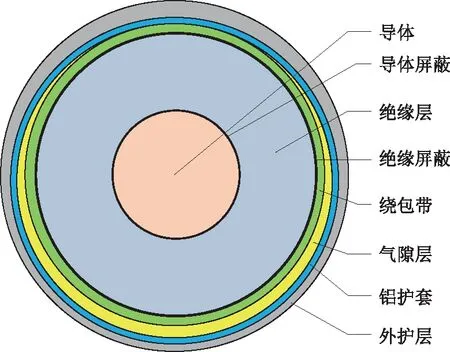
图1 YJLW0364/1101×500电缆横截面Fig.1 Cross-section of YJLW0364/1101×500 cable
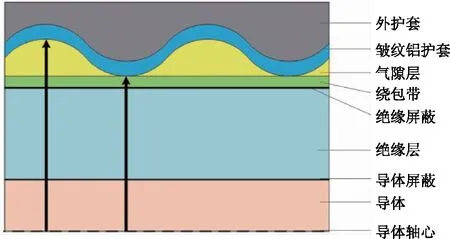
图2 YJLW0364/1101×500电缆纵截面Fig.2 Lengthwise section of YJLW0364/1101×500 cable
由图1和图2可知,电缆的皱纹铝护套为螺旋式前进结构,且在横截面上是偏离电缆轴心的圆环,圆环少数点与绕包带直接接触,大部分点与气隙层空气接触。另外,由于绕包带的蓬松状结构,紧密接触的点在实际结构中为一个小区域。电缆包覆层的这种结构与刘刚、雷成华等学者提出的观点具有相似性[22]。
综上所述,由于电缆的绕包带、气隙层、皱纹铝护套这3层结构有所交互,导致内部传热类型复杂多样,在构建热路模型时不能将其单独串联处理,而将3层合并为包覆层统一处理,可以忽略其内部结构及内部传热方式,建立更为清晰简单的热路模型。
1.2 传统暂态热路模型
传统热路法计算电缆载流量时,包覆层被分为绕包带、气隙层、皱纹铝护套3层作串联处理,根据文献[20]可知,当绝缘层分层数大于10时其计算误差减小不明显,故将绝缘层及内外屏蔽分为10层。电缆暂态热路模型如图3所示。图3中:T1为电缆导体表面实时温度,T2—T11为导体绝缘各分层外表面实时温度,T12为绕包带外表面实时温度,T13为皱纹铝护套实时温度,To为电缆表面实时温度,单位均为℃;C0为电缆导体热容,C1—C10为绝缘层(含内、外屏蔽)各分层热容,C11为绕包带热容,C12为气隙层热容,C13为皱纹铝护套热容,C14为外护套热容,单位均为J/K;R1—R10为绝缘层(含内、外屏蔽)各分层热阻,R11为绕包带热阻,R12为气隙层热阻,R14为外护套热阻,单位均为K/W;P为电缆导体损耗,单位为W。
这种模型是假设绕包带、气隙层、皱纹铝护套构成了从内而外的3层同心圆筒壁结构,3层结构的传热方式是在热传导的条件下构建的。然而该假设与电缆的实际结构和传热方式有较大出入,尤其是独立气隙层引入的过大热阻必然给传统暂态热路模型带来较大的误差。
1.3 优化暂态热路模型
根据文献[21]可知,绝缘层外侧的温差在1.5 ℃以内,相对极差为2.8%,在工程误差5%的允许范围内,可以假设绝缘层外侧为等温面。金属铝护套由于良好的导热性能,其外侧也近似为等温面。结合以上的分析以及传统建模假设,提出的优化建模假设如下:
a)绝缘层外侧温差较小,故假设电缆绝缘层外侧面为等温面。
b)假设铝护套为理想传热体,其外侧为等温面;皱纹铝护套整体上与导体同心,铝护套外侧面与导体同心,其半径为波峰和波谷的平均值。
c)将绕包带、气隙层、皱纹铝护套合并为一层包覆层,不再考虑其中复杂的结构及传热方式,其内外侧传热方式均为热传导。
d)忽略层间接触热阻,即假设各层之间紧密接触。
e)忽略温度变化时电缆各个参数的变化,即不考虑温度变化时电缆几何参数的变化以及材料热参数的变化。
f)因为内、外屏蔽层较薄,且热参数与绝缘层相近,建模时将内、外屏蔽层归并为绝缘层的一部分。
g)忽略导体的多芯纽绞线结构,假设导体为实心圆柱体。
h)单根单芯电缆载流时铝护套涡流和环流很小,忽略其损耗;绝缘层的损耗相较于导体损耗较小,因此也忽略。
i)假设电缆足够长且不考虑弯曲情况,忽略其轴向传热。
由以上假设得知,导体外侧、绝缘层外侧、铝护套外侧及电缆表面均为等温面,并且各个面同心,因此电缆可以简化为4层的中心对称结构。根据电缆结构及温度分布的对称性,以及忽略其轴向传热的情况下,可假设电缆仅存在径向温度梯度,由此构建出导体-绝缘层(含内、外屏蔽)-包覆层(绕包带、气隙层、皱纹铝护套)-外护套的一维优化传热模型。由此避免了对包覆层复杂内部结构的划分与传热分析,对传统暂态热路模型进行了优化设计。优化后的暂态热路模型如图4所示。图4中:C11为包覆层热容,R11为包覆层热阻,T11为包覆层实时温度,其他热容、热阻、损耗、温度与传统模型相同。
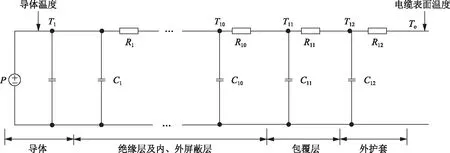
图4 优化的电缆暂态热路模型Fig.4 Optimized transient thermal circuit model of cable
根据热路与电路的相似性,对暂态热路模型中每一节点列热平衡方程,如下:
(1)
式中:n=12,为电缆暂态热路模型中总的节点数;i=1,2,…,9;τ为时间。
将上述方程组转换为矩阵形式,有
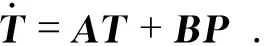
(2)
方程组的解为
(3)
式中ξ电缆内部初始温度矩阵。
式(2)和(3)中涉及的各个矩阵如下:
(4)
(5)
(6)
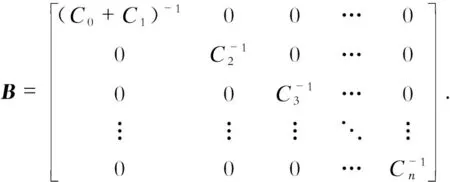
(7)
(8)
式(6)—(8)中矩阵A、B、P不具有物理含义,只是为了便于计算机编程计算。
根据IEC标准[12,23-24],计算出优化暂态热路模型中导体、绝缘各分层以及外护套的热容热阻参数,再根据电缆的载流温升实验计算包覆层热参数,即可确定矩阵A、B。编辑MATLABA程序,导入电缆表面温升曲线以及通过电缆的电流,即可确定矩阵P,并计算出电缆线芯的温升曲线。
1.4 暂态热路模型中参数的确定
1.4.1 导体发热功率计算
电缆导体的发热功率[12]
P=I2R.
(9)
式中:I为导体实时负荷电流;R为工作温度下导体交流电阻。其中[12]
R=R′(1+ys+yp).
(10)
式中:R′为导体的直流电阻;ys为集肤效应因数;yp为邻近效应因数,对于单根单芯电缆yp=0。其中[12]
R′=R′0×[1+α(θ-20 ℃)].
(11)
式中:R0′为20 ℃时单位长度电缆导体的直流电阻;α为导体的电阻温度系数,标准软铜α=0.003 92;θ为工作温度。
集肤效应因数[12]
(12)
(13)
式中:ks为经验值,取值1;f为电流频率;xs为系数。
1.4.2 热阻计算
1.4.2.1 绝缘层热阻计算(分为10层计算)
电缆绝缘层各层热阻[23]
(14)
式中:Rk为由内而外导体绝缘第k分层热阻(k=1,2,…,10),单位为K/W;dki为电缆绝缘各分层的内侧面直径,单位为mm;ρT为绝缘层热阻系数,单位为K·m/W;h1为绝缘层分层每一层厚度,单位为mm。本文采取等厚度的方法对绝缘层进行分层计算。
1.4.2.2 包覆层热阻的计算(通过测量数据计算)
测量稳态时导体和铝护套温度,即可通过式(15)计算出包覆层的热阻
(15)
式中:T′12为稳态时铝护套外侧温度,单位为℃;T′1为稳态时导体温度;P′为稳态时导体损耗,单位为W。
1.4.2.3 外护套热阻计算
外护套的热阻[23]
(16)
式中:d6为外护套外侧面直径,单位为mm;h2为外护套的厚度,单位为mm;ρ6为外护套热阻系数。
1.4.3 热容计算
依次计算各层热容,绝缘层分10层计算其热容,包覆层热容通过实验测量结合逼近法获取。
1.4.3.1 导体热容参数计算[24]
(17)
式中:dc为铜导体直径;δc为铜导体体积热容,单位为J/(m3·K)。
1.4.3.2 绝缘层各分层热容计算
采用式(18)对绝缘层各分层的热容进行计算[24]:
(18)
式中:δPE为绝缘体积热容;dko为第k层外侧面直径。
1.4.3.3 包覆层热容计算
采用逼近法确定电缆包覆层的热容。根据热路法的实际物理意义,在热路中其他参数均已知的前提下,C11必然存在唯一的正实数,使得式(3)成立,即模型计算的导体温度等于测量的导体温度。但由于测量等误差,测量导体温度与模型计算导体温度必然存在偏差σ,当σ满足给定条件,即可认为此时C11为可行解。
选择合适的包覆层热容C11初值,结合其他已知参数,计算出tj时刻电缆导体温度值T1tj,对比同时刻载流温升实验记录的导体温度值T′1tj,计算整个温升过程中测量导体温度与模型计算导体温度的偏差σ。不断修正C11值,直到偏差满足式(19),此时C11的值即为包覆层热容值。
(19)
由于绝缘层体积热容大于包覆层任何一层材料的体积热容,为此以绝缘层体积热容计算包覆层热容初值[24]:
(20)
式中d2为绝缘层外径。
以绝缘层的体积热容计算包覆层初值,其初值必然偏大,以递减的方法来逐渐修正C11,直到满足式(18)为止,此时的热容值即为包覆层热容。递减方法遵循的公式如下:
C11,m=(1-0.01)m-1C′11.
(21)
式中m表示修正的次数加1。当C11,m满足式(19)时,其值即为C11的值。
1.4.3.4 外护套热容计算
外护套的热容[24]
(22)
式中:C12为外护套热容;δ6为外护套体积热容。
2 测量与验证实验
本实验包括包覆层热参数测量和优化暂态热路模型验证实验。前者采集电缆包覆层热参数计算所需的数据;在假设同一类型的电缆具有相同包覆层热参数的前提下,验证实验采用同一类型电缆验证优化模型的准确性,2个实验相互独立。在包覆层热参数测量实验中,将采集到的电缆稳态时导体温度和铝护套温度代入式(15),计算出包覆层的热阻参数;再将电缆表皮温升数据、导体温升数据以及包覆层热容的初值,结合式(19)—(21),计算包覆层的热容参数。
为了验证优化暂态热路模型的有效性,选用同一类型的电缆进行加载与测量实验相同电流的温升实验,得到电缆导体和表皮温升曲线,然后通过传统暂态热路模型和优化暂态热路模型,由实验表皮温升曲线分别计算得到导体温升曲线,再与实验导体温升曲线进行比较,从而验证优化暂态模型的准确性和合理性。
2.1 实验系统
本实验系统由380 V电源、调压器、PLC控制柜、计算机操作台、升流器、电流互感器、补偿电容箱和电缆组成,如图5所示。本次实验电缆型号为YJLW0 64/1101×500。实验采用热电偶以及无纸记录仪采集电缆各层的温度。在电缆本体上打孔,埋入热电偶以测量电缆内部各层温度;将热电偶紧贴电缆表面即可测量其表面温度。为减小热电偶介入式测温带来的误差影响,在测温之前对热电偶进行校正实验,并采用环氧泥对钻孔处作密封处理。
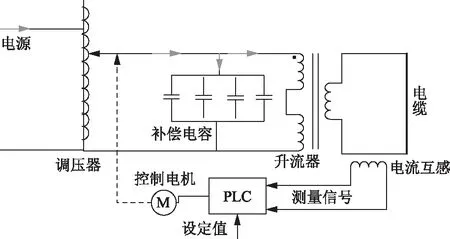
图5 实验系统原理Fig.5 Schematic diagram of experimental system
2.2 包覆层热参数测量实验
选择给定型号的实验电缆进行载流温升实验,加载电流为1 000 A,采集电缆表面温度等数据并导入MATLAB程序,计算电缆包覆层的热阻热容参数。电缆达到稳态时,导体温度为66.9 ℃,皱纹铝护套温度为42.5 ℃,计算导体损耗得37.56 W。将上述参数结合式(15)计算得到包覆层的热阻R11=0.155 2 K/W。而传统暂态热路模型下采用IEC标准计算得到的包覆层热阻为0.792 7 K/W。
采用式(20)计算包覆层的热容初始值C′11=5 980.1 J/K,将基于此初值计算得到的电缆导体温度以及实验测得的导体温度代入式(19)进行计算。经过2次修正后,σ≈0.329 5<1,符合要求,包覆层热容参数C11=5 861.1 J/K。而传统暂态热路模型下采用IEC标准计算得到的包覆层热容为1 527.2 J/K。
2.3 验证实验
选择并更换与测量实验同类型的单芯高压电缆,加载1 000 A电流再一次进行载流温升实验,持续到稳态,记录整个实验过程电缆导体以及电缆表皮的温升曲线,如图6所示。
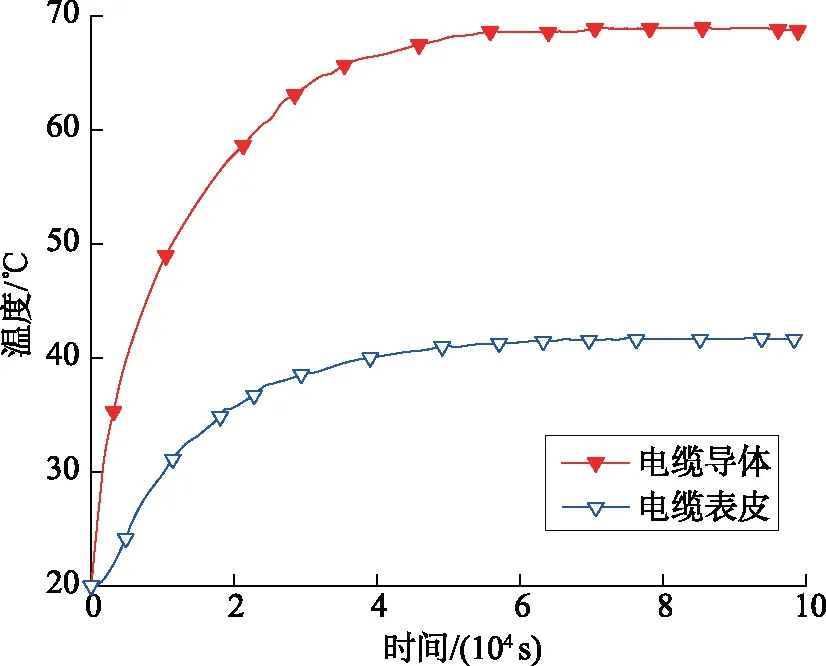
图6 电缆导体、表皮温升测量曲线Fig.6 Measuring curves of temperature rise of cable conductor and skin
3 讨论与分析
3.1 暂态热路计算导体温升曲线
编辑MATLAB程序,结合测量的包覆层参数,基于电缆表皮温升曲线分别计算传统热路模型和优化热路模型下的导体温升曲线,二者有明显的差异,如图7所示。
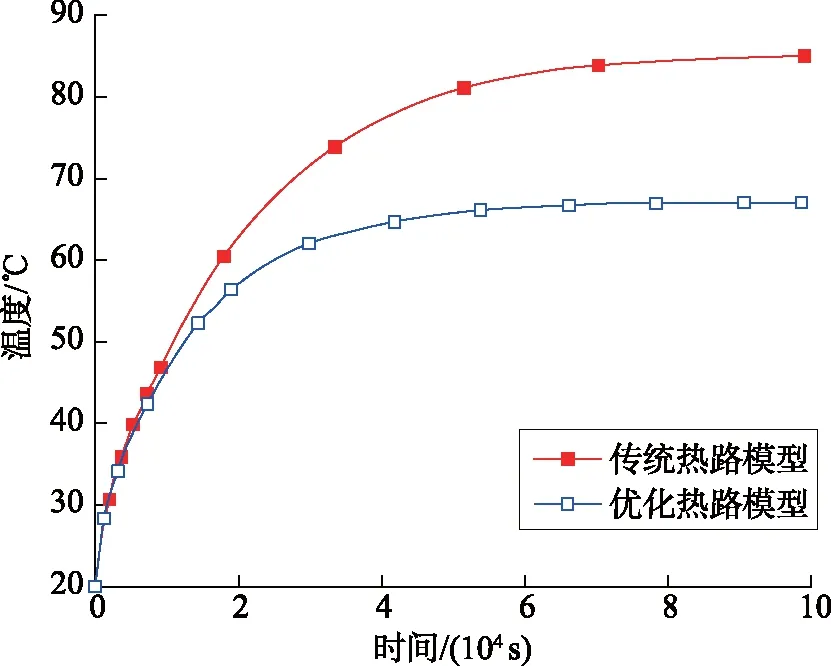
图7 传统、优化热路模型计算的导体温升曲线Fig.7 Conductor temperature rise curves calculated by traditional and optimized thermal circuit models
3.2 仿真导体温升曲线
为了进一步验证优化暂态热路模型的有效性,采用COMSOL仿真软件,依据传统建模假设构建传统仿真模型,即导体-绝缘层(含内、外屏蔽)-绕包带-气隙层-皱纹铝护套-外护套结构的电缆模型,电缆各层的参数设置见表1。将电缆导体设置为电磁热源,加载与实验相同的工频电流,电缆外表面与空气接触,符合传热的第3类边界条件,即对流边界条件,根据文献[13]将对流换热系数设置为12.5 W/(m2·K)。依据优化建模假设构建优化仿真模型,即导体-绝缘层(含内、外屏蔽)-包覆层-外护套结构的电缆模型,包覆层的热阻热容参数根据2.2节的计算值设置,其余设置与传统仿真模型相同。仿真计算对应2种仿真模型的导体温升曲线,规律与热路模型计算类似,如图8所示。
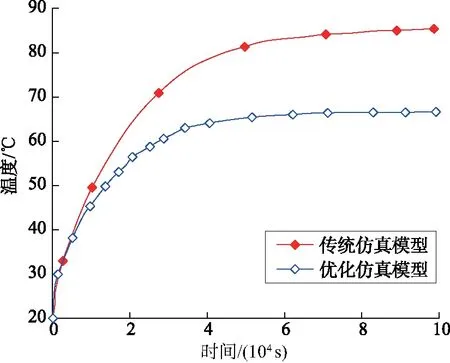
图8 传统以及优化仿真模型下的导体温升曲线Fig.8 Conductor temperature rise curves under traditional and optimized simulation model
3.3 对比分析
为了直观分析不同方法计算的导体温升曲线和实验测量结果之间的差异,将优化前后的模型计算、仿真计算导体温升曲线及测量导体温升曲线绘制在同一图中进行比较,如图9所示。
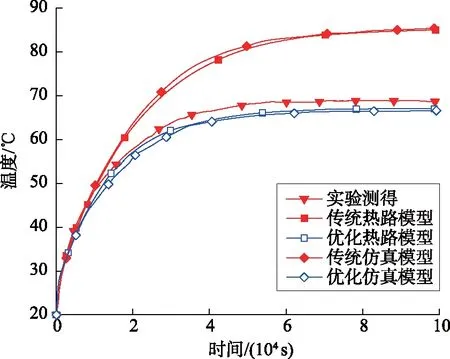
图9 不同方法得到的导体温升曲线Fig.9 Conductor temperature rise curves obtained by different methods
由图9可知,传统热路模型计算的导体温度远大于实测温度,主要是过大的气隙层热阻造成的。而采用优化热路模型计算得到的导体温升曲线更加接近实际测得的导体温升曲线,仿真分析得出同样的结论。优化前后热路模型计算和仿真计算结果差异不大,在稳态阶段二者差异接近于0。而优化后的热路模型计算结果和仿真模型计算结果与实验结果仍存在微小差距,这主要是由于采用热电偶介入式测温带来的误差影响。由此可见,导体温度计算的准确度主要取决于模型的假设与构建,不合理的模型会带来更大的计算误差。
3.4 误差分析
将测量得到的导体温度与仿真计算得到的导体温度进行误差分析处理,分析二者之间的绝对误差与相对误差。
3.4.1 绝对误差
由图10可以看出,传统与优化模型的绝对误差曲线变化规律不一样,这是由于优化模型采用集中参数代替分布参数。在导体温升阶段,模型不同,误差规律亦不同。优化模型计算的绝对误差最大值为2.7 ℃,随着温度缓慢上升,误差逐步减小,并最后趋于稳定值1.4 ℃;优化模型仿真在暂态时的绝对误差最大值为2.9 ℃,趋于稳态时为1.8 ℃;模型计算比仿真具有更高的精度,主要是仿真难以模拟环境的变化,给定的环境温度设置增大了计算误差。
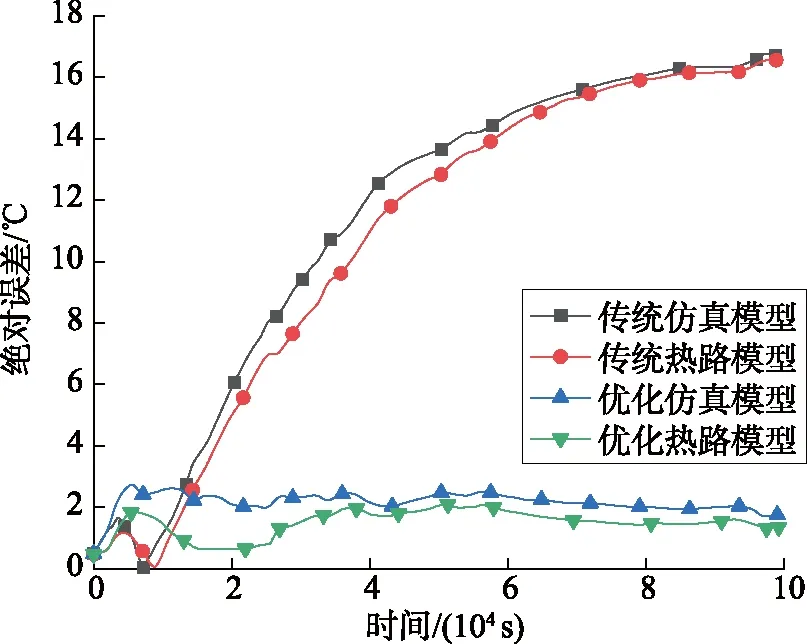
图10 不同方法得到的导体温升绝对误差曲线Fig.10 Absolute error curves of conductor temperature rise obtained by different methods
相比于优化模型的计算和仿真结果,传统模型计算和仿真结果误差较大,并且随着温度上升而变大,稳态时传统模型计算达到16.4 ℃,传统模型仿真为16.6 ℃。原因是气隙层的串联处理使得包覆层热阻过大,绕包带、气隙层、皱纹铝护套3层串联结构使得包覆层热容过小。
3.4.2 相对误差
不同方法得到的导体温度相对误差变化曲线如图11所示。
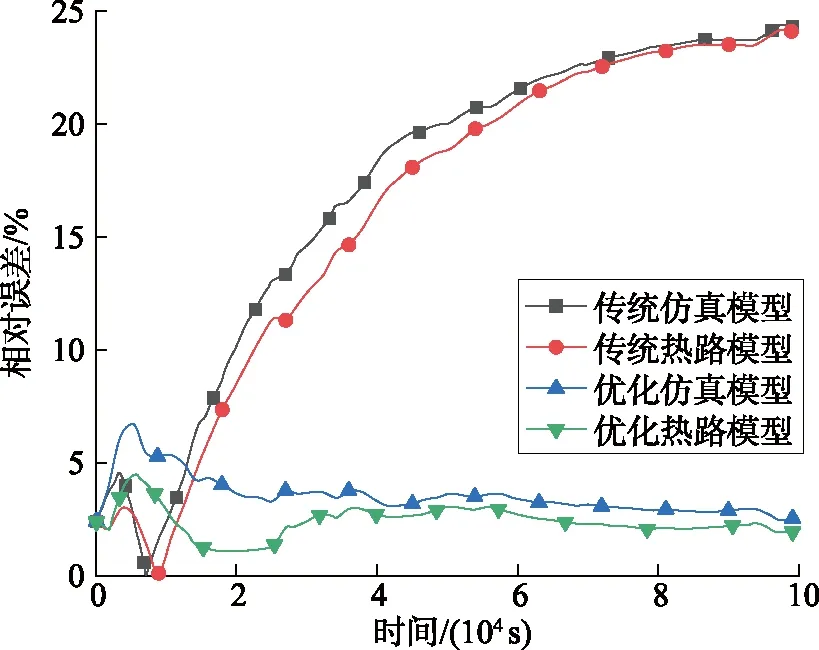
图11 不同方法得到的导体温升相对误差曲线Fig.11 Relative temperature error curves of conductor temperature rise obtained by different methods
由图11可知,相对误差与绝对误差有相同的变化规律。其中传统模型计算和仿真的最大相对误差分别为24.06%和24.33%,远远超过工程允许的误差5%。而优化模型仿真的导体温度最大相对误差为6.69%,稳态时趋近于4.15%,优化模型计算对应的分别为4.45%和2.31%,显著提高了模型的计算精度。
4 结论
本文首先从高压单芯电缆的实际结构分析,指出传统暂态热路模型将包覆层中的绕包带、气隙层、皱纹铝护套视为相互独立结构串联建模的局限性,并提出将绕包带、气隙层、皱纹铝护套合并为一层包覆层统一建模的优化暂态热路模型方法。以YJLW0364/1101×500电缆为例,理论分析传统暂态热路模型计算导体温度造成较大误差的原因,结合计算、仿真、实验评估优化后暂态热路模型的准确性和合理性,得出以下结论:
a)由热路计算结果可知,传统暂态热路模型下的包覆层热阻为0.792 7 K/W,热容为1 527.2 J/K,优化暂态热路模型下的包覆层热阻为0.152 2 K/W,热容为5 861.1 J/K。传统模型气隙层的串联处理使得包覆层热阻增大,绕包带、气隙层、皱纹铝护套,这3层串联结构使得包覆层热容减小,造成导体计算温度偏高。
b)结合热路计算结果、仿真结果、实验结果可知,传统暂态模型计算和仿真得到的导体温度最大绝对误差为16.4 ℃和16.6 ℃,最大相对误差为24.06%和24.33%;优化暂态模型计算和仿真得到的导体温度最大绝对误差下降为2.7 ℃和2.9 ℃,最大相对误差下降为4.45%和6.69%,显著提高了模型计算精度。

