Three-dimensional time-varying sliding mode guidance law against maneuvering targets with terminal angle constraint

Xinxin WANG, Hongqin LU,*, Xinlin HUANG, Yefeng YANG,Zongyu ZUO

a Center for Control Theory and Guidance Technology, Harbin Institute of Technology, Harbin 150001, China

b The Seventh Research Division, Beihang University, Beijing 100191, China

KEYWORDS Guidance law;Maneuvering target;Terminal angle constraint;Three-dimensional;Time-varying sliding mode

Abstract This paper deals with the problem of intercepting maneuvering targets with terminal angle constraints for missiles subjected to three-dimensional non-decoupling engagement geometry.To achieve the finite-time interception and satisfactory overload characteristics,a time varying sliding mode control methodology is developed based on a time base generator function.The main feature of the proposed guidance law guarantees the Line-of-Sight (LOS) angles to converge to small neighborhoods of the desired values at the interception time. First, a fractional power extended state observer is used to estimate the unknown target acceleration, which can significantly reduce the adaptive switching gain. The fractional power extended state observer enjoys the advantage of better noise tolerance.Then,a newly designed sliding mode surface is constructed by introducing a time base generator function and the time-varying sliding mode guidance law is developed based on this time-varying sliding surface. The proposed guidance law significantly reduces the overload magnitudes.Numerical simulations are carried out to verify the performance of the proposed guidance law.

1. Introduction

With the development of modern guidance,designing the guidance laws with the terminal angle constraint has attracted a huge deal of research attention.During the past few decades,the Proportional Navigation (PN) method is extensively utilized in designing guidance laws with terminal angle constraints due to its simple form and easy implementation.As for the task of intercepting high maneuvering targets, the PN guidance laws are difficult to fulfill the requirements of high-precision guidance. Besides, the Optimal Control (OC)has been also applied in designing terminal angle constrained guidance laws.Nevertheless, these OC guidance laws require accurate information on the target acceleration and the time-to-go estimate when intercepting a maneuvering target.Apart from the PN guidance laws and OC guidance laws,the sliding mode control provides a new approach to design the guidance laws as a result of its robustness to external disturbances.There are several guidance laws with terminal angle constraints through the sliding mode control.Note that these guidance laws only concern the asymptotical stability.

Since the terminal guidance time is very short, it is necessary to design guidance laws with finite-time convergence.To achieve the finite-time convergence,Terminal Sliding Mode(TSM)-based guidance laws with terminal angle constraints were presented.However, a singularity may exist due to the negative exponent term. Hence, a NTSM-based (Nonsingular Terminal Sliding Mode-based) guidance law was presented to intercept the maneuvering targets at a desired terminal angle to deal with the singularity problem while providing the finite-time convergence.A finite-time bang-bang type guidance law based on the Linear Sliding Mode (LSM)was proposed for intercepting maneuvering targets.The results in Refs. 15,16, however, require the accurate upper bound of the target acceleration in advance, which is difficult to accurately measure in the actual battlefield scenario. An effective way is to use the adaptive technique to estimate the target acceleration upper bound.A guidance law was proposed to intercept the maneuvering targets with the terminal angle constraint via the NTSM and the adaptive control.Nevertheless, large adaptive switching gains are required in this result for guaranteeing the robustness of the closed-loop system, which will in turn, increase the energy consumption and induce the undesired chattering. An alternative way is to estimate the ternal disturbance through an observer, which can reduce the gain significantly. Using the observers for estimating and compensating the unknown target acceleration, guidance laws with terminal angle constraints were proposed for intercepting maneuvering targets.However, these guidance laws have two main limitations.First,these guidance laws were only designed for the planar case. Second, the estimate accuracy of the observers may drop sharply when there is the measurement noise with an adverse impact on the performance of the guidance law.

The targets are intercepted by the missiles in the threedimensional (3D) space, and the model correctly describing the relative motion of the missile and the target is highly nonlinear and coupled.However, in most of the existing results, the 3D guidance laws were designed for two mutually orthogonal planar engagements decoupled from the 3D engagement affecting the guidance accuracy.Several terminal angle constrained guidance laws for intercepting maneuvering targets have also been designed for the non-decoupling 3D model. A 3D cooperative guidance for multiple missiles was developed to intercept maneuvering targets at desired LOS angles. This work requires the upper bound of the target acceleration to guarantee the robustness of the closed loop system, which restricts its practical application.A 3D guidance law was proposed based on the adaptive integral sliding mode control against maneuvering targets.Nevertheless,the terminal angle constraint was not taken into consideration. Based on the NTSM and adaptive control,some finite-time 3D guidance laws with terminal angle constraints were proposed.Nonetheless, these designs require large adaptive switching gains to guarantee the robustness of the closed-loop system.To overcome this drawback,observer-based 3D guidance laws were presented for intercepting the maneuvering targets.However, the estimate accuracy of the observers may also be influenced by the measurement noise.

The convergence time derived in the above finite-time guidance laws depends on the initial states, whether they are designed for the planar case or the 3D case. Large gains in these guidance laws are required to achieve the fast convergence when the initial error is large.Hence, the initial acceleration of the missile is large which may cause an input saturation problem and consume much more energy. Polyakov presented a so-called fixed-time stability, which ensures that the convergence time is bounded regardless of the initial conditions.Recently, many fields have developed the fixedtime controllers including the multi-agent consensus,the air-to-ground missile control,and the spacecraft formation control.Particularly, two different fixed-time terminal angle constrained guidance laws were proposed by using the fixedtime NTSM and the adaptive control to intercept maneuvering targets.These works, however, have two two main shortcomings. (1) Large adaptive switching gains are required to guarantee the robustness of the closed-loop system. (2)These two fixed-time guidance laws only concern the planar case. Note that there exists a common limit in the aforementioned fixed-time control methods: a large magnitude of initial control input. This is owing to existence of the specific structure, i.e., a power which is larger than one.Therefore,the system may occur an input saturation which would weaken the performance of the system. In recent years, Time Base Generator (TBG)-based controllers have been developed in Refs.. These TBG-based controllers have two main features. (1) The settling time is independent of the initial conditions and the convergence region of the system state can be regulated to a desired level via tuning a TBG gain.(2) The amplitude of the controller can be restricted in a reasonable range by selecting a proper TBG gain. In Refs.,two time-varying sliding mode guidance laws were proposed with impact angle constraints where the Linear Extended State Observer (LESO) was employed to estimate the unknown target acceleration. However, these two guidance laws were only designed for the planar case and the performance of the LESO will deteriorate when there is the measurement noise. To the best of our knowledge, there may be no three-dimensional time-varying sliding mode guidance law which is design for intercepting maneuvering targets and has good performance in restraining the measurement noise.

Motivated by the above discussion,this paper is devoted to designing a three-dimensional terminal angle constrained timevarying sliding mode guidance law for intercepting maneuvering targets with high precision although there exists the measurement noise. First, we design a fractional power extended state observer to estimate the unknown target acceleration.Then,a new sliding mode surface is constructed by introducing a TBG function and the 3D time-varying sliding mode guidance law is developed based on the designed sliding mode surface. The main contributions of this paper are as follows.

(1) Compared with the time-varying guidance laws in Refs.,which were only designed for the planar case,this guidance law is derived by using coupled 3-D model,which shows great potential in the practical application.

(2) Different from the conventional three-dimensional finite-time guidance laws based on TSM, the presented guidance law employs the Time Varying Sliding Mode(TVSM) based on a TBG function driving the system states to converge to small neighborhoods of the desired values at the interception time. Consequently, the large overloads at the initial stage can be avoided by consuming less energy.

(3) Compared with the LESO utilized in the existing results,this guidance law adopts the Fractional Power Extended State Observer (FPESO) to estimate the target acceleration, which enjoys the advantage of better noise tolerance.

The rest of this paper is organized as follows. The preliminaries and the problem formulation are given in Section 2. In Section 3, the proposed guidance law is developed in detail,followed by the several simulations in Section 4. Finally, a brief conclusion is presented.

2. Preliminaries and problem formulation

2.1. Preliminaries

Lemma 2. Consider the system (3), if the control law is constructed as in Eq. (4), then the system state p（t ） converges into the region

Remark 1. It can be observed from Eq.(5)that the size of the convergent region can be determined by the values of δ and κ.Since δ ≪ξ（0 ）, the size of the convergent region can be decreased to a desired level by choosing a sufficiently small δ and large κ.

2.2. Problem formulation

This part concerns a 3D engagement geometry of the target and the missile. For simplicity, the target and missile are regarded as constant-velocity point masses. The engagement geometry is shown in Fig. 2, where OXYZand OXYZdenote the inertial reference frame and the LOS reference frame, respectively. OXYZand OXYZdenote the body coordinates for the target and missile, respectively. Vand Vrepresent the velocities of the target and missile,respectively. ϑ, ψand ϑ, ψrepresent the pitch and yaw path angles of the missile and target, respectively. r, θand φare the relative distance between the missile and the target,the elevation,and azimuth angles of the LOS to the inertial reference frame, respectively. The target and missile motions in the inertial reference frame are obtained as:target and missile. Based on the parallel approach principle,the objective is to establish a guidance law guaranteeing a small miss distance of the missile, the LOS angle errors e（i=1，2） and the relative velocities perpendicular to the LOS, i.e., V（i=1，2） converge to small enough neighborhoods of the origin at the interception time while existing the unknown target acceleration.

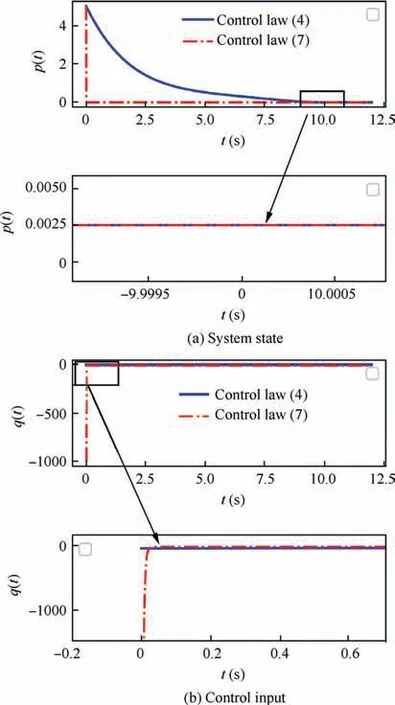
Fig. 1 Curves of system state and control input under two control laws.

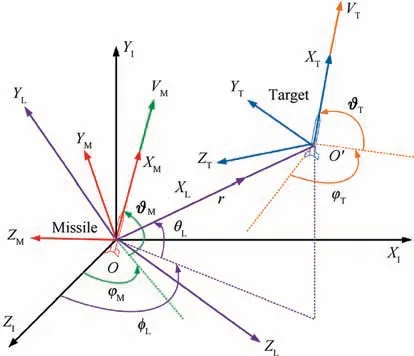
Fig. 2 3D engagement geometry.

3. Guidance law design

The guidance dynamics are strongly coupled,highly nonlinear,and time varying. Moreover, the target maneuver is also unknown in practice.By difficulties arising from these aspects,it becomes essential to involve these aspects in the 3D guidance law design. Therefore, this study deals with the unknown target maneuver and the terminal angle constraint.In this section,a novel 3D Time Varying Sliding Mode Guidance Law(TVSMGL) is developed. Firstly, to estimate the external disturbances caused by the unknown target acceleration, a FPESO is proposed. Then, the TVSMGL is designed based on a novel time-varying sliding mode surface with a TBG function.

3.1. Fractional power extended state observer

3.2. Time-varying sliding mode guidance law

Based on assumption 2, r is a small positive constant at the interception time, i.e., ris a small positive constant. Since the objective here is to make the LOS angle errors e（i=1，2） and the relative velocities V（i=1，2） converge into small neighborhoods of the origin at the interception time,we can choose the prescribed time instant as t=t,in which tis interception time.Thus,a feasible selection of the TBG function is given as ξ（t ）=r-r. Based on Lemma 2, a timevarying sliding mode surface can be built as follows:

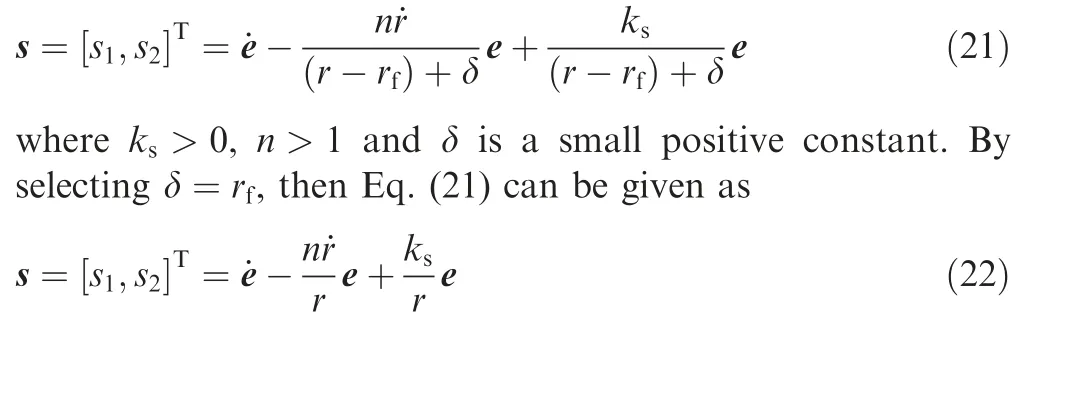
Remark 2. Note that the TBG function ξ（t ）in the control law(4)should satisfy ˙ξ （t ）=0 when t>tto ensure the continuity of the control law at the time instant t. In this paper, this condition is not necessarily satisfied since we selected the prescribed time instant as the final time of the interception.

(1) The LOS angle errors e（i=1，2） will converge into small neighborhoods of the origin at the interception time.

(2) The relative velocities perpendicular to the LOS, i.e.,V（i=1，2） ultimately converge into small neighborhoods of the origin at the interception time.

Remark 3. It should be noted that the TVSMGL in Eq.(24)is discontinuous as a result of the presence of a signum function resulting in undesirable chattering.To alleviate the chattering,we replaced the signum function in Eq.(24)with the following continuous smooth function:

Remark 5. There is a close relation between the TBG function ξ（t ） and the TVSM method recommended in this study. The choice of ξ（t ）is not unique.The different choice of ξ（t ）results in different convergence performances, which can make the design of guidance law more flexible.

3.3. Theoretical analysis of the proposed guidance law

This article aims at designing a terminal angle constrained guidance law which entails the missile to intercept maneuvering targets in 3D space. The main innovation of this guidance law is that it enables the LOS angles to approach to their desired values at the interception time such that it possesses good overload characteristics.Now we give a detailed analysis of the proposed guidance law.The expressions for aand acan be obtained by expanding as follows:

4. Simulation results

According to Eq. (24), the parameter parameter n should satisfy n-1>0,i.e.,n>1.Here,we choose n=1.8.According to the sliding mode surface in Eq.(22)and the convergence region of the LOS angle error e in Eq. (40), the value of kshould satisfy r≪k≪r（0 ）. Since r（0 ）=15000 in the simulation and ris a small constant and usually satisfies r＜1.Hence, we select k=100. Since the estimate error of the FPESO is bounded and not large,the value of K is not appropriate to choose too large.Here,we select K=8.The choice of the parameter τ should integrate the satisfactory chattering suppression and high control accuracy. Here, we select τ=0.002. According to Refs. 44,45, the parameters kand kshould satisfy k>0 and k>0. Here, we choose k=2 and k=3. The parameter ϑ should satisfy ϑ ∈ （0.5，1） and we select ϑ=0.7. Ref.46 pointed out that the Extended State Observer (ESO) would have satisfactory performance when 0.01 ＜μ ＜0.1. Here, we choose μ=0.02. Furthermore, the larger the bandwidth of the ESO is, the larger the disturbance amplitude the ESO can track and the larger the influence of the noise is. Therefore, we should select the bandwidth λ by integrating the estimable disturbance amplitude and the influence of the noise. Here, we select λ=40. In order to show more clearly, we list the design parameters of the proposed TVSMGL in Table 1.

Table 1 Parameters of the proposed TVSMGL.

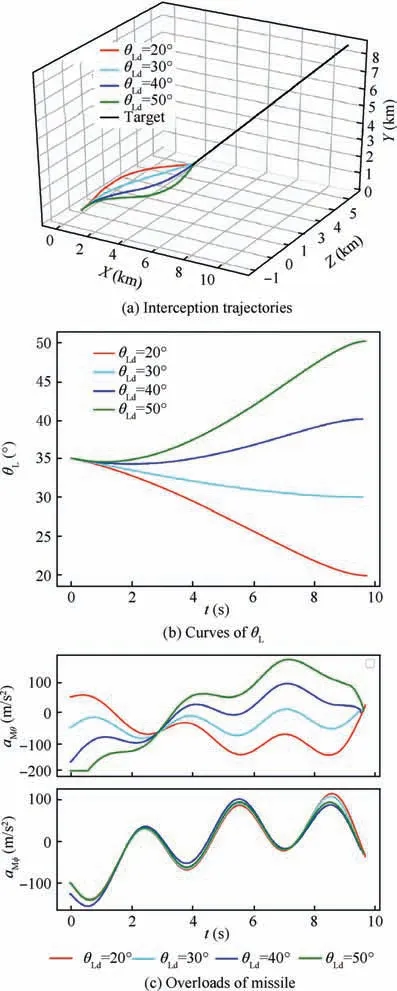
Fig. 3 Simulation results under TVSMGL:θLd =20°，30°，40°，50° when φLd =-30°.

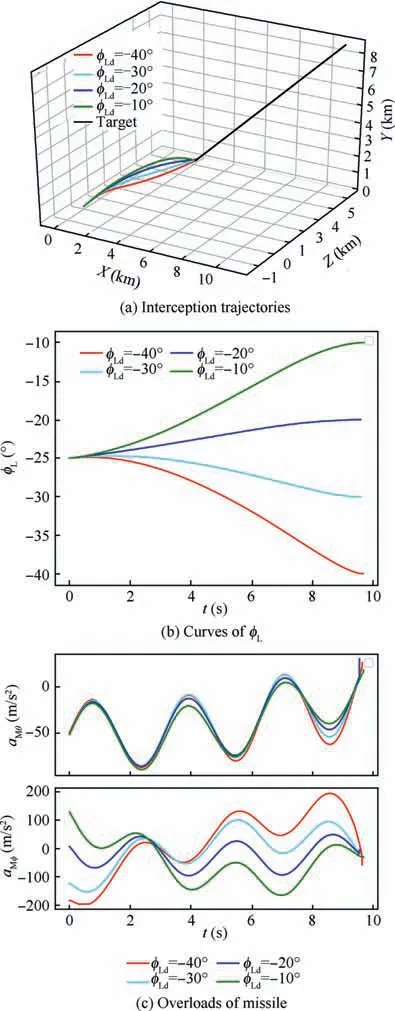
Fig. 4 Simulation results under TVSMGL: φLd =-40°，-30°，-20°，-10° when θLd =30°.

4.1. Terminal angle constraint test

Here, the simulation results of sinusoidal target interception with various preferred impact LOS angles are provided. The accelerations of the target are set as a=6gsin（2t ）m/s,a=6gsin（2t ）m/s. The desired LOS angles are θ=20，30，40，50when φ=-30and φ=-40，-30，-20，-10when θ=30.

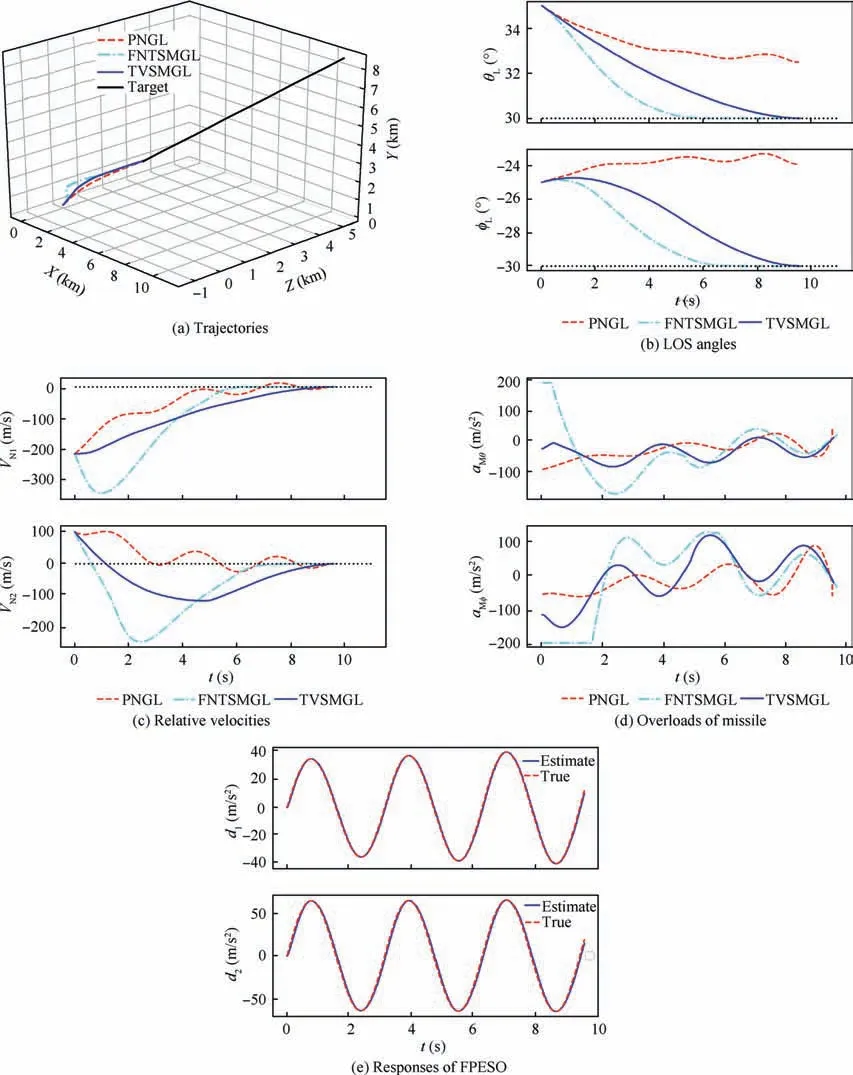
Fig. 5 Simulation results under three guidance laws of Case 1.

The simulation results are illustrated in Figs. 3-4. Fig. 3(a)and 4(a)show the interception trajectories,Fig.3(b)shows the terminal LOS angle θ,Fig.4(b)shows the terminal LOS angle φ, and Figs. 3(c)and 4(c) represent the profiles of the missile overloads.It can be seen from Figs.3(a)and 4(a)that the missile can successfully intercept the target with different desired LOS angles. As Figs. 3(b) and 4(b) clearly show, the LOS angles approach to their desired values at the interception time. Figs. 3(c) and 4(c) indicate that the characteristics of the overloads is satisfactory. Moreover, the miss distances,the interception times, and the LOS angle errors are listed in Tables 2 and 3. We can conclude from Tables 2 and 3 that the miss distances and the LOS angle errors with variousdesired LOS angles are sufficiently small verifying the terminal angle constraint property of the proposed guidance law.Moreover, the interception time and the overloads are subjected to the LOS angle error.The larger error leads to the longer interception time and the larger overloads.

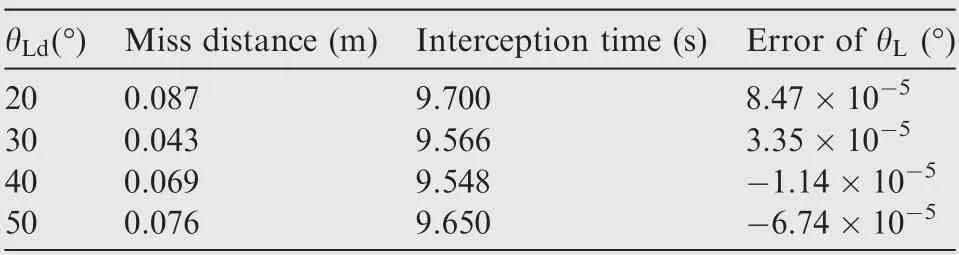
Table 2 Miss distances,interception times and errors of θL for various θLd when φLd =-30°.

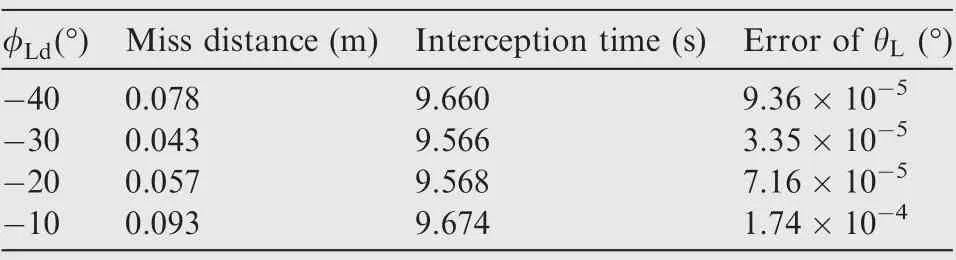
Table 3 Miss distances, interception times and errors of φL for various φLd when θLd =30°.

4.2. Comparison with other guidance laws

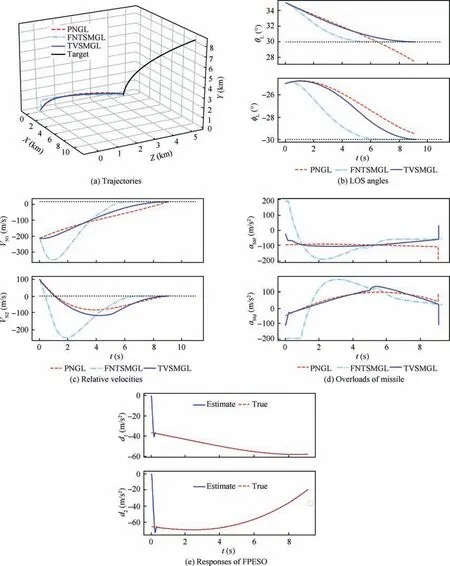
Fig. 6 Simulation results under three guidance laws of Case 2.

In this part, the desired LOS angles are set as θ=30,φ=-30.The comparisons are made by using Proportional Navigation Guidance Law (PNGL) and the Finite-time Nonsingular Terminal Sliding Mode Guidance Law(FNTSMGL).The PNGL can be expressed as

where the parameter N is set as 5.

The nonsingular terminal sliding mode surface is designed as

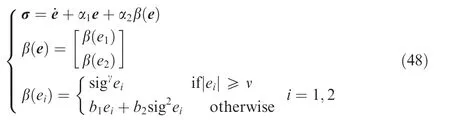
where sige= |e|sign（e）, b= （2-γ）ν, b= （γ-1）ν,0 ＜γ ＜1, α, αand ν are positive constants.

Fig. 7 Simulation results under three guidance laws of Case 3.

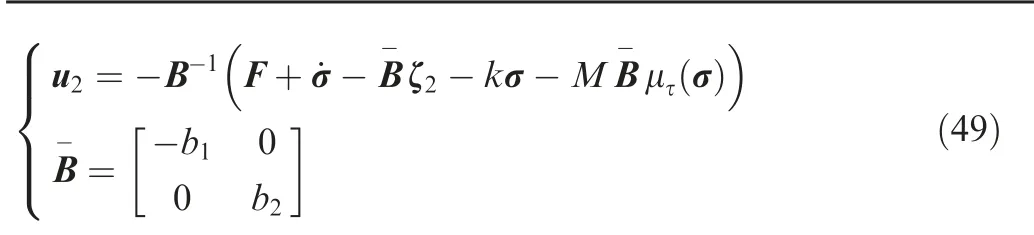
The corresponding FNTSMGLis presented as pared to the TVSMGL. The reason is that the large gains are adopted in FNTSMGL to guarantee the convergence while the TVSMGL is constructed based on a TBG function and time-varying robust terms. Accordingly, the trajectories under

where ζis the same as that in Eq. (16). The parameters of FNTSMGL are selected as α=α=0.2, γ=0.7, ν=0.005,k=5, M=10 and τ=0.002.

Three cases for the various target accelerations are chosen as follows:

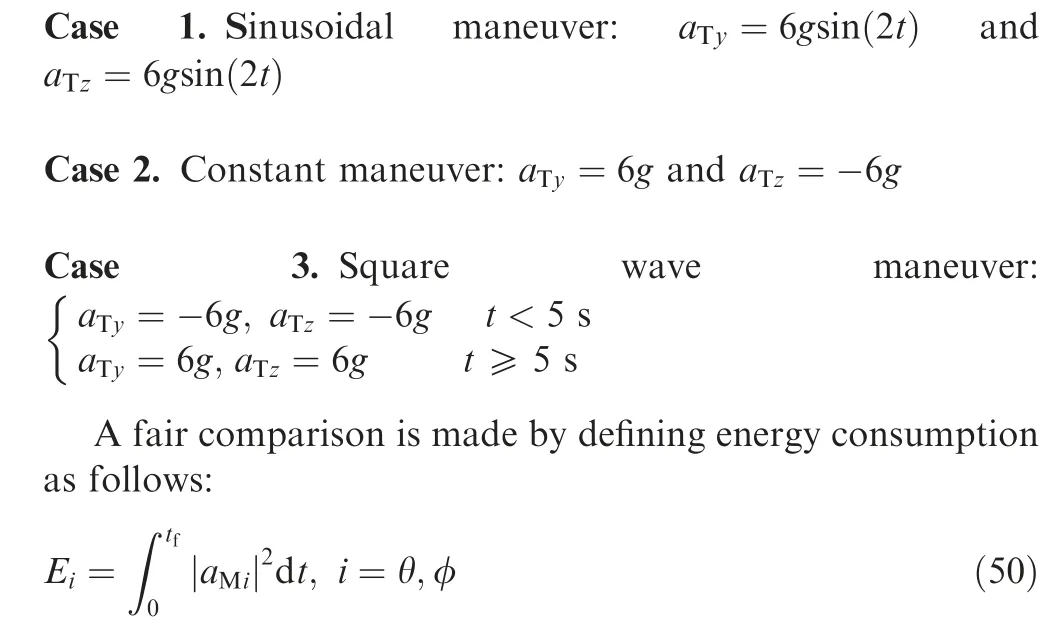
where tis the interception time.

The simulation results of the three cases are shown in Figs. 5-7 including interception trajectories, LOS angles profiles,relative velocities perpendicular to the LOS,missile overloads,and responses of the FPESO.From Figs.5(a)-7(a),it is observed that all of these three guidance laws can assure effective interception. The trajectories under the PNGL and the TVSMGL are smoother and shorter compared to the FNTSMGL.The LOS angles curves in Figs.5(b)-7(b)demonstrate that the FNTSMGL and the TVSMGL can make the LOS angles approach to their desired values in contrary to the PNGL verifying the terminal angle constraint property of the FNTSMGL and the TVSMGL. Furthermore, the FNTSMGL makes the LOS angles converge more rapidly than the TVSMGL. Figs. 5-7(c) indicate that all these guidance laws can ensure the relative velocities perpendicular to the LOS converge to small neighborhoods of the origin.However, the FNTSMGL ensures the relative velocities converge more quickly than the PNGL and the TVSMGL. Fig. 5(e)-7(e) reveal the disturbance estimation, it is observed that the estimates approach to the real values as soon as possible denoting the satisfactory performance of the FPESO.The missile overloads’ profiles are represented in Figs. 5(d)-7(d) indicating that the FNTSMGL causes the actuator saturation.Tables 4-6 list the miss distances, LOS angle errors, interception times,and energy consumption under these three guidance laws. According to Tables 4-6, the miss distance and the LOS angle errors under the PNGL in these three cases are much larger compared to the FNTSMGL and the TVSMGL. The reason is that the PNGL can hardly deal with the maneuvering target while the TVSMGL and the FNTSMGL adopt the FPESO for estimating the target acceleration better compensating for the influence of the target maneuver. The miss distances under the FNTSMGL are close to those of the TVSMGL. Moreover, under the TVSMGL, the LOS angle errors are smaller than those of the FNTSMGL.Furthermore,the energy consumed by the FNTSMGL is much larger com-the FNTSMGLin Figs. 5(a), 6(a) and 7(a) are more tortuous than those of the TVSMGL. Besides, the convergence rates of the LOS angles under the FNTSMGL shown in Figs. 5(b),6(b)and 7(b)are faster compared to the TVSMGL.Therefore, the overload curves are in Figs. 5(d), 6(d) and 7(d) saturation for a long time under the FNTSMGL and the energy consumption obtained by the FNTSMGL is much larger than the TVSMGL.

Table 4 Miss distances, interception times, LOS angle errors and energy consumption of Case 1.

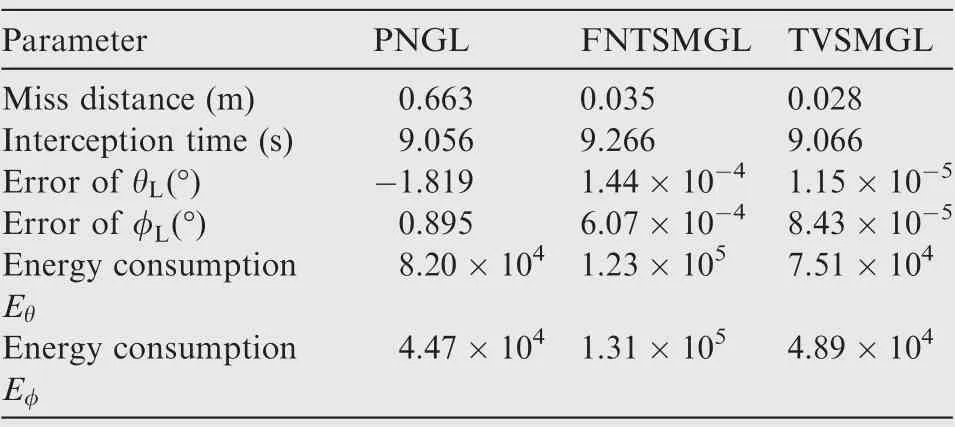
Table 5 Miss distances, interception times, LOS angle errors and energy consumption of Case 2.

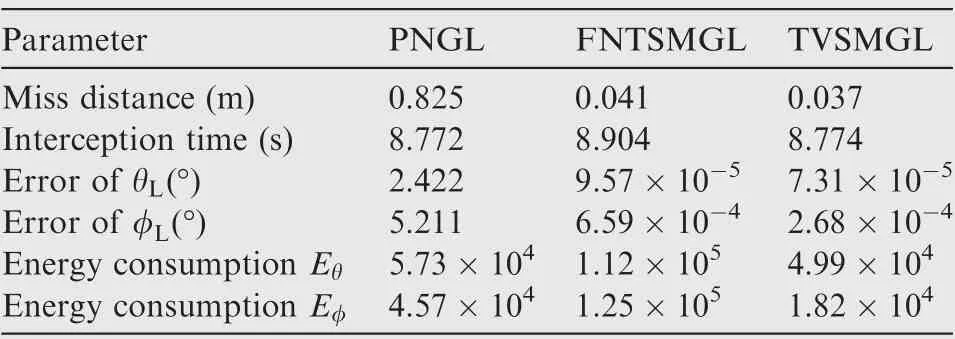
Table 6 Miss distances, interception times, LOS angle errors and energy consumption of Case 3.

Fig. 8 Responses of FPESO and LESO without noise.

Table 7 Miss distances and LOS angle errors for the comparison of FPESO and LESO.

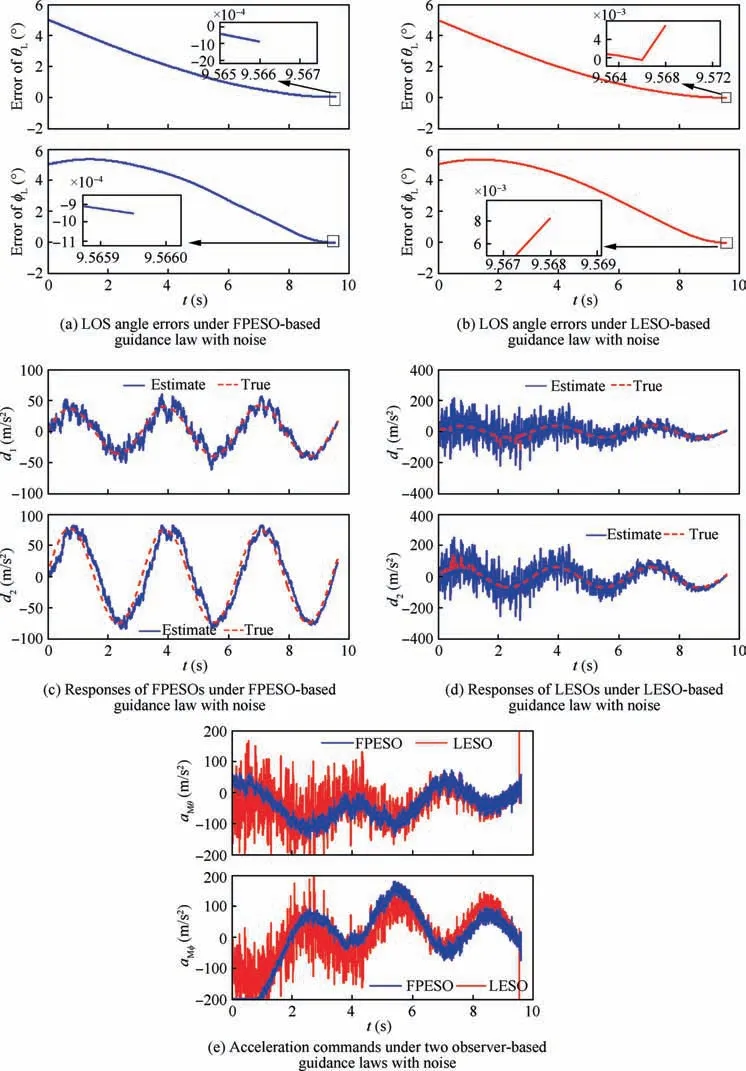
Fig. 9 Simulation results under two observer-based guidance laws with noise.

From the above simulation results, we can conclude that the proposed TVSMGL includes the following two advantages.First,the TVSMGL can realize terminal LOS angle constraint precise interceptions compared to the PNGL.The miss distance and the LOS angle errors under the PNGL are obviously larger than those of the TVSMGL. Second, compared with the FNTSMGL, the TVSMGL owns better overload characteristics and consumes much less energy with a similar guidance precision and smaller tracking control precision.

4.3. Test the performance of the FPESO

To examine the performance of the FPESO and the linear extended state observer (LESO), a comparison is made. The FPESO in Eq. (24) is replaced by the LESO, and the rest remains the same. Motivated by the Refs. 1,38,39, the LESO is designed as follows:

where the parameters of the LESO-based guidance law are selected as the same as the FPESO-based guidance law, i.e.,n=1.8, k=100, K=8, and τ=0.002.

Here, the desired LOS angles are set as θ=30,φ=-30. The accelerations of the target are set as a=6gsin（2t ）, a=6gsin（2t ）. The simulation results of these two extended observers(Fig.8)indicate that the estimate accuracy of the FPESO is much higher than that of the LESO with the same bandwidth λ when there is no measurement noise.The miss distances and the LOS angle errors under these two observer-based guidance laws without noise are listed in Table 7. According to this table, the miss distance and the LOS angle errors obtained by the FPESO-based guidance law are slightly smaller compared to the LESO-based guidance law.This is because that the estimate accuracy of the FPESO is higher than that of the LESO with the same bandwidth λ.Generally, the measurement information obtained by the seeker contains noise,and the signal-to-noise ratios of the LOS angular rates are much smaller compared with the relative distance.We assume that the LOS angular rates contain the Gaussian white noise with the standard deviation equal to σ=0.05（）/s.Fig.9 represents the simulation results including the LOS angle errors, the responses of the observers and the missile acceleration commands. Furthermore, the miss distances and the LOS angle errors under these two observerbased guidance laws with noise are also listed in Table 7.Figs.9(a)and(b)reveal that the LOS angle errors under the FPESObased guidance law is smaller than those of the LESO-based guidance law. Figs. 9(c) and (d) indicate that the effect of the noise on the FPESO is much smaller than the LESO, which implies that the FPESO benefits better measure noise tolerance. The curves of the acceleration commands in Fig. 9(e)clearly indicate that the guidance commands with the FPESO are much smoother compared to the LESO. Table 7 demonstrate that the miss distance and the LOS angle errors under the FPESO-based guidance law are much smaller compared to the LESO-based guidance law with noise. We can theoretically analyze that the FPESO has better performance in measurement noise suppression. From the second line of Eq. (16),the λ-dependent term of the FPESO is λ.Since θ ∈ （0，1 ）,we have ϑ+1 ＜2,hence,λcan be smaller than λin the LESO for a large λ. Based on the simulation results, the FPESObased guidance law can realize a smaller miss distance, and the LOS angle errors are smaller than those of the LESObased guidance law particularly for the case with noise. This verifies that the FPESO has better performance than the LESO in reducing the estimation error and noise suppression.

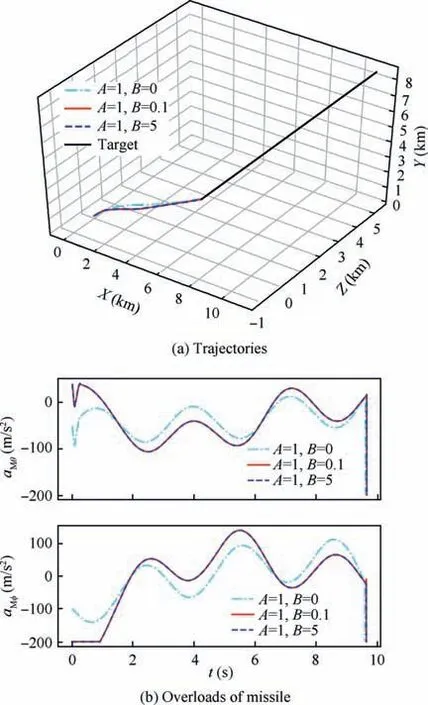
Fig. 10 Simulation results with ξ （t ）=Ar+Br2.

4.4. Different choice of TBG function

In this part, the desired LOS angles are set as θ=30,φ=-30. The accelerations of the target are set as a=6gsin（2t ）, a=6gsin（2t ） and the TBG-function ξ（t ） is selected as r-rin the implementation of guidance law in Eq. (24). As mentioned in Remark 5, ξ（t ） is not unique and yields a huge deal of flexibility in the guidance law design.To confirm this property,the results with various ξ（t ）are analyzed in this part. We choose ξ（ t ） as the second-order polynomial of r-r, which is expressed as

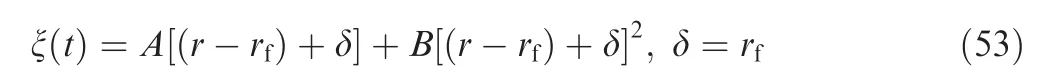
where the coefficient A is set to 1 and the coefficient B is selected as 0,0.1 and 5,respectively.Fig.10 represents the simulation results including the trajectories of the target and the missile and the overloads of the missile. It is observed that the trajectory is the shortest and the overloads are the smallest when B=0. Moreover, the curves of the case B=0.1 and B=5 are almost coincident. The reason is that the term Brin Eq.(53)is dominant when r is large and the term Ar is dominant when r is small. From Eq. (53), we have

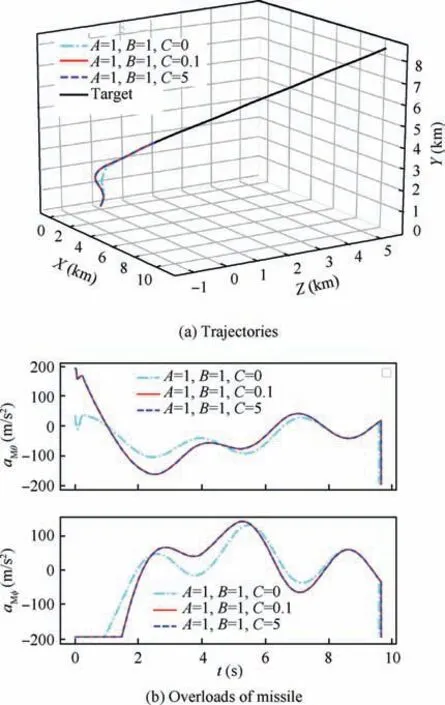
Fig. 11 Simulation results with ξ（t ）=Ar+Br2+Cr3.

According to Eq. (54), the overloads of the case B≠0 are larger than when B=0. From Eq. (54), we can obtain that ˙ξ（t ）/ξ（t ） is slightly changed for different B when B≠0. Thus,the curves of the cases B=0.1 and B=5 are almost coincident.

Then,we select the ξ（t ）as the third-order polynomial of r,which is explained as

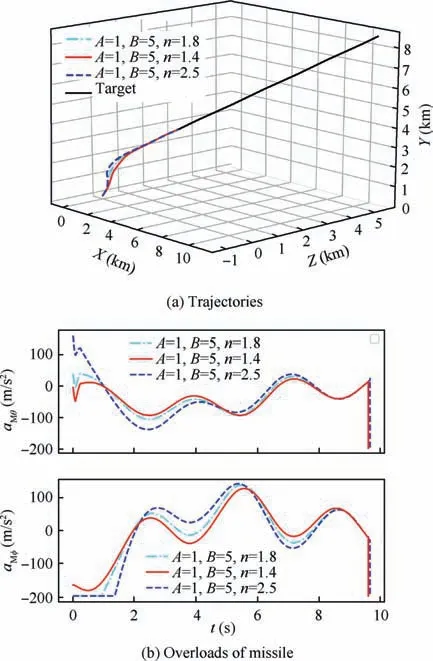
Fig. 12 Simulation results: ξ（t ）=Ar+Br2, n=1.8，1.4，2.5.

5. Conclusions

This study proposes a three-dimensional TVSMGL with terminal angle constraints for a missile intercepting maneuvering targets in the 3D engagement geometry. The proposed TVSMGL guarantees the LOS angle errors and the relative velocities perpendicular to the LOS to converge to small neighborhoods of the origin at the interception time.The details can be summarized as follows:

(1) A time-varying sliding surface is constructed with a TBG function, then the TVSMGL is developed based on the time-varying sliding surface. The large overloads are not included by TVSMGL at the initial stage compared to the finite-time guidance laws based on the conventional NTSM.

(2) The FPESO is used to estimate the unknown target acceleration significantly reducing the adaptive switching gains. Compared to the LESO, the FPESO shows better performance in the estimation accuracy and noise suppression.

(3) The effectiveness and the superiority of the proposed TVSMGL are verified by the theoretical proofs and simulation results.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

s

This study was co-supported by the National Natural Science Foundation of China (Nos. 61673034 and 62073019).