圆柱头盘形悬式瓷绝缘子钢脚结构优化分析

周学明，尹骏刚，胡丹晖，王森林，朱广飞，王德福，肖汉宁

(1.国网湖北省电力有限公司电力科学研究院，武汉430077；2.湖南大学，长沙410082；3.湖南湖大华龙电气与信息技术有限公司，长沙410205；4.山东淄博电瓷厂股份有限公司，山东 淄博 255129)

0 引 言

近年来，在运盘形悬式瓷绝缘子劣化率偏高，炸裂[1-3]甚至断串[4-6]等事故时有发生，对电网安全稳定运行构成了严重威胁。运行绝缘子劣化是电气、机械和环境因素综合作用的结果。目前，国内外学者针对瓷绝缘子电气性能评估开展了大量研究，包括绝缘子电场分布仿真和检测研究[7]、电路模型及电路传输特性研究[8]、绝缘子零值[9-11]、污闪[12-13]及冰闪特性研究[14]等。针对瓷绝缘子机械性能评估也开展了大量研究，涉及静态及动态载荷下应力特性[15-17]、形变特性[18-19]、振动疲劳性能[20-21]、覆冰故障率[22]、大吨位瓷绝缘子运行状态评估[23]以及极端外部环境下输电线路综合风险评估[24]等。

盘形悬式瓷绝缘子头部结构可分为圆锥形和圆柱形两种。我国输电线路上目前所使用的悬式瓷绝缘子大多数为圆锥头结构；但近年来圆柱头绝缘子的使用量显著增加。电气性能方面，圆柱头和圆锥头结构的内、外绝缘性能在理论上无本质差别[25]。机械性能方面，圆锥头绝缘子受部件材料性能经时变化的影响大，易受这种变化的作用而改变产品的结构配合或造成较大应力集中。而圆柱头绝缘子对于这种变化有较好的分散和调整能力，使其影响显著减小，且不在产品中累积，从而使得产品不受过大应力及不均匀应力的长时作用，具有较高的可靠性[26-27]；并且，圆柱头产品瓷件形式统一，机械化成型中无过多切削过程，因而十分适合模具成型。

据统计，在运悬式瓷绝缘子断串的主要原因是其自身质量问题[28-29]。鉴于技术成本等因素，提升部件材料自身性能变得愈发困难；因此，绝缘子结构的优化设计已成为提升其产品可靠性的关键。为提高绝缘子产品机械性能，通常可增大头部内眼尺寸与壁厚。但该方法会造成头部尺寸过大，铁帽与瓷件质量增加。圆柱头绝缘子头部结构几乎无锥角，因而只能通过优化钢脚结构来实现应力应变尽可能分布均匀。通过有限元分析优化绝缘子产品结构是十分有效的手段[30-31]。本研究在不改变绝缘子铁帽及瓷件结构的前提下，建立钢脚参数化的精细仿真模型，通过有限元法计算分析钢脚几何参数对圆柱头瓷绝缘子机械性能的影响，为产品优化提供设计参考。

1 绝缘子仿真模型

1.1 固体力学计算理论

笔者以某厂家出产的某型120 kN圆柱头瓷绝缘子产品为研究对象，其仿真模型见图1。

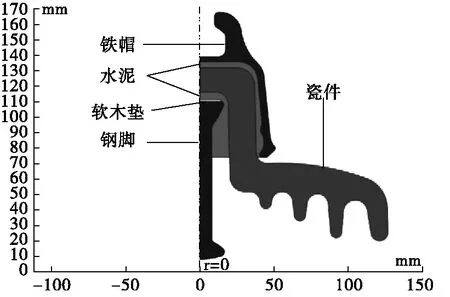
图1 某型圆柱头瓷绝缘子仿真模型示意图Fig.1 Schematic diagram of simulation model of a type of cylindrical head porcelain insulator

该模型结构力学仿真基于线弹性材料假设，遵循如式(1)所示的固体力学方程。式中，F为变形梯度，S为第二类皮奥拉-基尔霍夫应力，FV为体积力，u为位移场，I为预应力，Finel为非弹性变形梯度贡献；Ji为非弹性体积比，ε为应变张量，C为柯西-格林张量，E为杨氏弹性模量，ν为泊松比，Sad为预应力张量。

(1)

为使模型受力符合实际工况，模型需在铁帽头部内侧添加固定约束,且在绝缘子钢脚处添加相应的载荷。其约束方程如下：

(2)

式中，n为边界单位法向量，FA为边界载荷，A为边界面积，Ftot为总力；其值如下：

(3)

式中FN为绝缘子额定载荷，取值为120 kN。

相关材料参数设置见表1。

表1 材料属性Table 1 Material properties

1.2 钢脚几何参数

笔者主要研究钢脚浸入水泥胶合剂的头部几何参数对绝缘子机械性能的影响。见图2，选取5个主要的几何参数进行分析，分别为根部弧半径R1，中段弧半径R2，顶部弧半径R3，钢脚头总高D1，钢脚头总宽D3。

图2 绝缘子钢脚结构参数示意图

2 仿真计算与分析

2.1 D3对绝缘子的影响

扫描参数D3，计算瓷件、钢脚和水泥中的应力应变分布。图3(a)、图3(b)反映的分别是瓷件和水泥随D3变化时，其最大应力和应变的变化规律；图3(c)、图3(d)反映的是D3在所示取值范围内分别取最小、最大值时的绝缘子应力云图。从图3(a)可以看出，D3参数在17 mm附近时瓷件上的最大应力出现极小值，而体积应变值在D3取值范围内都保持很低的水平。图3(b)反映了随着D3的增大，水泥胶合剂上的最大应力与体积应变都呈现相同的单调下降趋势。从图3(c)、图3(d)可以发现，随着D3的增大，瓷件上的最大应力点发生了移动，从圆柱根部内侧移动到头部内侧。

图3 D3对绝缘子的影响图Fig.3 Influence diagram of D3 on insulator

2.2 D1对绝缘子的影响

扫描参数D1，计算瓷件、钢脚和水泥中的应力应变分布。见图4(a)，钢脚头高度D1存在一个最优点使瓷件上的最大应力达极小值，其取值在19～20 mm之间。图4(b)表明，与D3类似，随着D1增大水泥胶合剂上的最大应力与体积应变都呈现相同的单调下降趋势。通过图4(c) 、图4 (d)可发现瓷件上的最大应力和最大应变点随着钢脚头部的伸长而上升；若钢脚头部太过靠近瓷件头部内壁，将引起瓷件头部转角处的应力集中。

图4 D1对绝缘子的影响图Fig.4 Influence diagram of D1 on insulator

2.3 R2对绝缘子的影响

扫描参数R2，计算瓷件、钢脚和水泥中的应力应变分布。通过图5(a)、图5(b)可发现随着R2的增大，瓷件和水泥胶合剂的最大应力和应变都随之增大；钢脚头部侧面的大弧若变为直线(R2值很大)，不利于绝缘子瓷件的受力。

通过图5(c) 、图5 (d)可看出随着R2弧半径增大，钢脚头部的侧面变得更加平直，最大应力朝圆柱根部移动而应变分布没有很大变化。从应力的角度考虑，尽量减小R2的半径，增大钢脚头部侧面的弧度，可以降低瓷件上的应力集中。

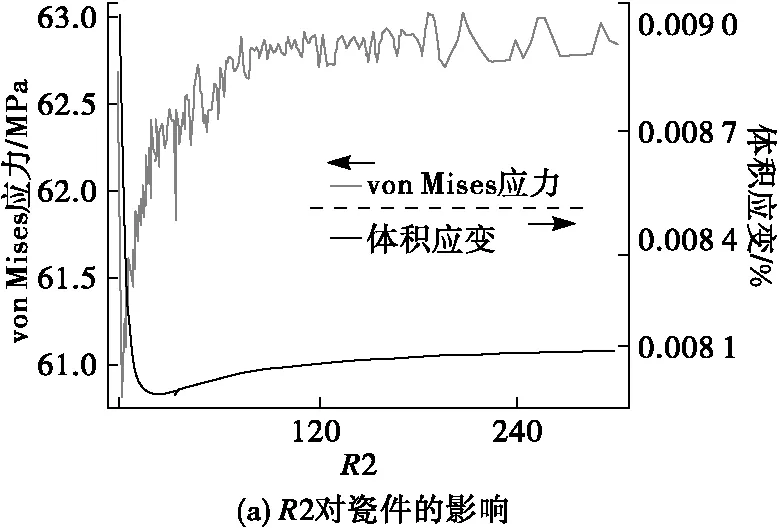
图5 R2对绝缘子的影响图Fig.5 Influence diagram of R2 on insulator

2.4 R3对绝缘子的影响

扫描参数R3，计算瓷件、钢脚和水泥中的应力应变分布。从图6(a)可看出，存在一个最优的R3值使瓷件上的最大应力达到极小值，其取值约为4 mm。

图6(b)反映了R3的增加会小幅降低水泥胶合剂上的最大应力。

通过图6(c)、 图6 (d)可以看出，随着R3的增大，瓷件中的最大应力点上移至瓷件到钢脚的近点。

图6 R3对绝缘子的影响图Fig.6 Influence diagram of R3 on insulator

2.5 R1对绝缘子的影响

扫描参数R1，计算瓷件、钢脚和水泥中的应力应变分布。经分析从图7(a)，发现随着R1的增大，瓷件上的最大应力也相应变大，而最大应变在R1较小时变化平缓，较大时快速增加；总之，在考虑瓷件应力的情况下，不宜选取较大的R1值。分析图7(b)可发现当R1超过3.6 mm后，水泥胶合剂中的最大应力和最大应变均出现一个阶跃式上升；超过9 mm后，又出现一个阶跃式下降；超过14.2 mm后，再次阶跃上升。通过分析发现，随着R1的增长，R1弧逐渐代替R2弧，使钢脚由外凸结构变为内凹结构，导致受力构型发生变化，从而引起最大应力和应变的阶跃式跳变。

图7 R1对绝缘子的影响图Fig.7 Influence diagram of R1 on insulator

从图7(c)、图7(d)可以发现，R1的变化并没有导致瓷件的最大应力分布发生明显的改变，对瓷件的影响较小。

2.6 综合分析

1)D3、D1分别为绝缘子钢脚头部半径及高度，两者控制钢脚头部尺寸，对绝缘子瓷件、水泥受力影响较大。D3、D1的设计应使钢脚头部不能过分远离或靠近瓷件。

2)R1，R2，R3三个半径分别对应绝缘子钢脚由直线朝头部曲线过渡的过渡弧(根部弧)和钢脚头部侧面的中部弧以及钢脚头顶部直线与中部弧衔接的顶部弧；三者控制钢脚头部侧面的形状和微小结构。

3)R2不宜过大(即对应的圆弧不应为直线)，较大的弧度可以有效优化绝缘子的应力分布。R3在允许的范围内取稍大的值能够优化瓷件柱头壁面上的应力分布，但R3过大会使钢脚头部靠近瓷件内壁，也会挤压R2的调整空间。R1对瓷件受力影响不大；但随R1变化，水泥的应力应变出现多次阶梯式跳变，R1取值不当将导致钢脚侧面受力形态发生质变，内凹的形态不利于钢脚将侧面的压力传递给瓷件的内壁，因此会对水泥胶合剂产生不利影响。

4)总体而言，仿真的所有参数均未对钢脚产生显著的影响，也未发现明显的变化规律。一方面因为钢脚的最大应力和应变都不在研究对象钢脚头部处；另一方面，钢脚被设计为承受远大于瓷件的应力，头部几何参数改变对钢脚受力的影响较小。

3 结 论

本研究针对某型圆柱头盘形悬式瓷绝缘子产品，建立了钢脚参数化的精细仿真模型，采用有限元法计算分析了5个主要的钢脚几何参数(钢脚头总高D1、钢脚头总宽D3、钢脚根部弧半径R1、中段弧半径R2、顶部弧半径R3)对绝缘子机械性能的影响，得出以下结论：

1)几何参数D3、D1控制绝缘子钢脚头部尺寸，对绝缘子瓷件受力的影响较大；R1、R2、R3对绝缘子瓷件受力的影响相对较小，但可通过适当调整改变应力应变分布，避免过度集中。

2)几何参数D3、D1、R1对水泥应力应变的影响较大。其中，D3、D1与应力应变均呈近似线性；随R1变化应力应变出现多次阶梯式跳变，因此R1的取值应慎重考虑；而R2、R3对水泥应力应变的影响较小。

3)所仿真的5个主要几何参数均未对钢脚产生显著的影响，也未发现明显的变化规律。

通过开展圆柱头瓷绝缘子有限元仿真计算，可为产品优化升级提供快捷有效的设计参考。