科技创新效率与区域经济韧性交互分析——基于珠三角地区的实证

王 鹏，钟誉华，颜 悦

(1.暨南大学 经济学院，广东 广州 510632；2.华南农业大学 经济管理学院，广东 广州510642)

0 引言

自我国实行改革开放政策以来，屡屡创造国内经济增长奇迹的“人口红利”逐渐消失，即将面临刘易斯拐点。从长期看，如何选择和转变经济增长方式成为促进我国经济稳定增长的关键[1]。转变经济增长方式的出路之一就是科技创新，即通过科技进步提高经济产出效率、优化产业结构、引领经济增长方式转型[2]。从党的十八大报告首次明确提出实施创新驱动发展战略、必须将科技创新摆在国家发展核心位置，到党的十九大报告提出创新是引领发展的第一动力及建设现代化经济体系的战略支撑，再到“十四五”规划明确提出全社会研发经费投入年均增长7%以上的指标要求，科技创新已经成为影响我国经济高质量增长的决定性因素。“十四五”时期作为承接两个百年奋斗目标的关键5年，是我国迈向第二个百年目标新征程的一个起点。当前，我国经济发展既面临重大机遇，同时也经历着前所未有的考验。新冠疫情全球大暴发、中美贸易摩擦加剧、国际逆全球化思潮抬头、西方技术封锁等外在因素不断冲击着我国经济发展，考验着我国的经济韧性。在新发展格局下，珠三角地区作为我国重要的经济腹地及科技创新示范高地，提高珠三角地区科技创新产出效率和转化效率，对于打破地区壁垒、促进区域经济高质量发展、强化区域经济韧性具有重要现实意义。基于此，本文从科技创新两阶段效率入手，使用非期望超效率SBM模型测算珠三角地区科技创新两阶段效率，引入区域经济韧性变量，分析两者之间的交互作用，可为提高珠三角地区科技创新效率提供理论支撑。另外，通过揭示区域环境对科技创新的影响作用，根据不同地区特点和发展水平制定差异化方案，能够更好地提高不同区域科技创新水平和经济发展韧性。

1 文献综述

1.1 从科技创新产出到科技创新效率

“创新”这一概念来源于Schumpeter[3]的创新理论，他强调生产技术革新对于促进经济发展的重要作用，认为创新是经济发展的本质。在新古典增长理论和内生经济增长理论中，技术同样被视为驱动经济增长的重要因素。在研究初期，大多数学者聚焦于科技创新投入产出水平，一类以专利权衡量科技创新产出，以量化科技创新产出水平。如Mueller[4]使用相关系数衡量行业内部科技创新投入与专利数之间的关系；另一类用R&D投入产出弹性系数研究科技创新对经济发展的促进作用。如Griliches[5]、Mansfield[6]、吴延兵[7]分别对美国、日本及中国制造业进行科技创新产出弹性测量，证实科技创新对生产率提升有显著促进效应；卢方元和靳丹丹[8]从区域视角研究发现，中国各区域R&D投入与经济增长存在长期、稳定的正相关关系且具有空间异质性特征。随着研究的不断深入，研究重点从科技创新是否促进经济产出到科技创新如何促进经济增长，再到科技创新投入冗余与转换效率上。Jones & Williams[9]通过构建一个包含R&D扭曲参数的内生增长模型，指出相对于社会最优水平，分散经济体科技研发投入不合理。中国东、中、西部地区科技创新效率存在显著的空间差异，高R&D投入地区资源配置不合理，甚至还出现R&D投入规模报酬递减[10]。而且，当前R&D规模对我国经济具有抑制作用，因此要重视R&D转换效率[11]。本文认为，科技创新衡量标准不仅应包括科学技术发明，还应涵盖其所带来的经济价值和社会价值。

1.2 科技创新与经济韧性

韧性一词近年来频频出现在区域经济学研究中。由于世界各地都在遭受不同类型的外部冲击，国家或地区在抵抗力和恢复力上存在显著异质性，这一现象引起学者广泛关注[12]，并由此引申出区域经济韧性的概念，以解释地区在面对外部冲击时的差异化表现[13]。目前，学界对区域经济韧性的定义尚未达成共识。Martin[14]从抵抗力、恢复力、适应力和创造力4个维度定义区域经济韧性；也有学者从城市角度出发，将经济韧性定义为当城市遭受外部冲击后恢复甚至超过原有发展水平的能力[15]。总的来说，区域经济韧性是指区域受到外部冲击后吸收、转换冲击的演化能力。现有文献对科技创新与经济韧性关系的研究主要聚焦科技创新对区域经济韧性的作用，大部分学者认为技术进步和积累对经济韧性发挥着不可替代的作用[16-18]，但也有学者持相反观点[19]。

综上所述，既有研究存在以下不足：第一，科技创新效率测量方法单一，评价科技创新效率的主要方法是绝对投入产出比或者DEA，未考虑投入冗余对结果造成的偏误。第二，科技创新系统是一个多投入多产出的多阶段过程，已有研究主要集中在科技创新系统内部投入产出效率上，缺乏对科技创新系统经济产出效率的研究。第三，将科技创新视为经济韧性影响因素，以这种固定视角研究两者之间的关系，忽略了经济韧性对科技创新的反馈效应，有可能导致内生性问题。第四，珠三角地区作为我国改革开放前沿及科技创新示范高地，对珠三角地区内部科技创新与区域经济韧性关系的研究较少。

鉴于此，本文主要解决如下问题：使用非期望超效率SBM模型对珠三角地区科技创新效率进行测度，通过构建联立方程组，分析科技创新两阶段效率与经济韧性之间的交互关系。而且，本文考虑到不同经济发展水平地区内部科技活动对经济韧性的敏感度不同，故根据《中国城市竞争报告》将珠三角地区划分为高发展水平地区和次高发展水平地区两个区域，前者包括广州、深圳、佛山、东莞，后者包括中山、珠海、肇庆、江门、惠州。

2 研究路径

科技创新活动是一个多投入多产出的“黑箱子”过程，当前学者对科技创新活动产出的研究主要集中在以下两个方面：一是将科技创新划分为直接经济产出和间接经济产出[20]；二是把科技创新划分为多个阶段(傅春等，2021)。本文将科技创新活动划分为科技创新成果产出和经济效益转化两个阶段，分别测量两个阶段的转换效率。同时，本文将区域经济韧性和产业结构多样化也纳入考量，重点探讨科技创新与经济韧性之间的交互关系，揭示三者之间的影响路径，如图1所示。

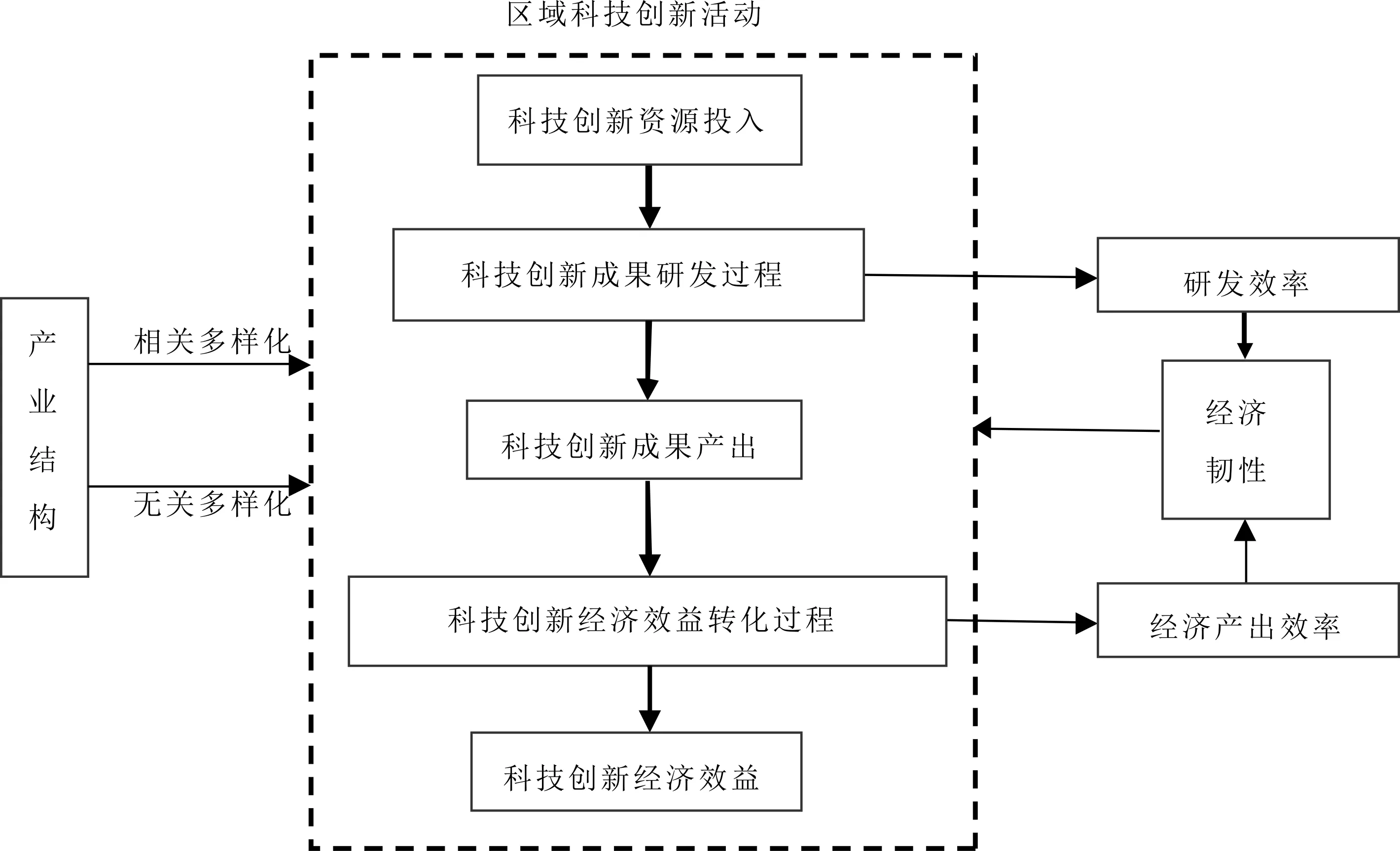
图1 科技创新与经济韧性关联路径Fig.1 Correlation path between scientific and technological innovation and economic resilience

本文以测量科技创新效率为出发点，分别测量科技创新系统成果研发和经济产出效率。科技创新与经济韧性之间并非单向影响关系，经济韧性可作为科技创新环境支撑影响科技创新效率，科技创新效率也可通过提高区域技术水平影响经济韧性；同时，科技创新亦有可能作为中介传导影响经济韧性。因此，本研究通过构建联立方程，研究经济韧性与科技创新两阶段效率之间的交互性，并且加入产业多样化作为两类方程的因变量，探讨其在经济韧性和科技创新两阶段活动中的影响路径。

3 科技创新效率测度方法与结果

3.1 研究方法

3.1.1 非期望超效率SBM模型

科技创新活动两阶段投入产出并不是单通道运行，每个阶段都具备多投入多产出的路径特征，为评估这种多投入多产出路径特征的转换效率，本文使用数据包络分析非参数估计法对数据进行检验，因其具有客观性、简化性和误差小等优势，在理论和实证研究中得以广泛运用。另外，DEA及其衍生的一系列测算模型。如super-DEA、SBM模型在科技创新效率测算方面也具有一定的可靠性和可行性[21-22]，因此本文选择非期望超效率SBM模型提供了理论支撑。

在DEA分析结果中只有当效率值等于1时，决策单元(Decision Making Unit，DMU)才有效，这就会导致同时出现多个有效的DMU效率值。由于科技创新存在投入过剩或产出不足的问题，因此基于松弛变量度量(Slacks-based measure，SBM)模型更符合科技创新系统特征，该方法不仅可以直接测量决策单元投入产出冗余，而且和普通DEA模型相比，更能体现过程效用最大化原则。在此基础上，本文结合超效率模型，使DMU有效值大于1[23]，以避免后续因素分析时产生数据上的缺陷。由于在经济转换阶段存在废气、污水等非期望产出，因此本文选择非径向非导向的CRS非期望超效率SBM模型进行测算，公式如下：

minρSE=

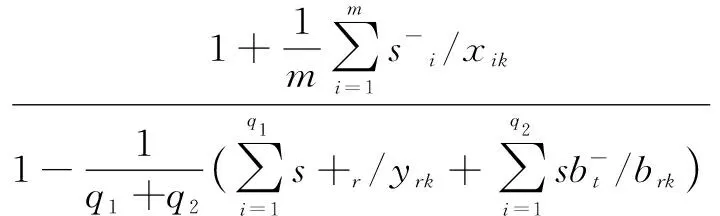
(1)

式(1)中，ρSE为系统效率值；x、y、b分别代表系统投入要素、期望产出要素和非期望产出要素的数值；m、q1、q2分别代表投入要素、期望产出要素和非期望产出要素的个数；i、r、t分别代表投入、期望产出和非期望产出决策单元；s-i、s+r、sb-t为松弛变量，λj为模型中的权重向量。ρSE数值决定系统产出效率，ρSE≥1说明系统有效；ρSE<1说明在系统内部转化过程中处于无效状态，可通过调整投入产出水平达到系统有效。

3.1.2 投入产出要素选取

本文在已有研究的基础上[24-25]，将科技创新投入划分为资金投入和人力投入，以地方财政科学事业费支出衡量科技创新资金支持、R&D活动人员衡量地区科技创新人力资本投入，其中R&D活动人员包括政府部门和规模以上工业企业活动人员；在科技创新成果产出方面，考虑到科技创新成果既有知识载体的特性，又具备一定的市场价值，因此选取发明专利授权量和新产品产值作为该阶段的产出指标；考虑到数据的全面性和代表性，本文还选取新产品出口额和地区生产总值作为经济转换阶段的期望产出指标，选取工业废水排放量、工业二氧化硫排放量和工业烟尘排放量作为非期望产出指标，具体指标如表1所示。

表1 两阶段效率评价指标Tab.1 Two-stage efficiency evaluation index

科技创新两阶段具有一定的时滞性，科技创新投入和科技创新成果产出存在累积效应，因此本文将地方财政科学事业费支出、专利授权量和新产品产值作为科技投入时考虑其有效累积量而非当期数量。本文参考刘汉初、樊杰和周侃[26]对科技创新滞后效应的测算，设置如下模型定义每一期的有效累积投入量。

(2)

3.2 数据来源与说明

本文数据主要来源于2002—2019年《广东省统计年鉴》,专利授权量数据来源于广东省市场监督管理局网站公示信息，个别数据来源于各市国民经济和社会发展统计公报和统计年鉴，部分缺失数据通过线性插值法补全。

由于《国民经济行业分类》在2011年和2017年有所修订，因此本文以2017年最新版《国民经济行业分类》作为行业分类标准；另外，《广东省统计年鉴》2009年以后相关数据统计口径由大中型工业企业改为规模以上工业企业，R&D活动人员指标包含规模以上工业企业R&D活动人员和政府部门R&D活动人员，因此本文中采用的新产品产值、新产品出口额统计对象都是规模以上工业企业。

3.3 科技创新两阶段效率测算结果

本文采用Matlab软件对各地区科技创新系统进行非期望超效率SBM建模分析，对科技研发阶段和经济产出阶段分别进行测算，科技研发阶段效率值测算结果如表2所示。从中可见，珠三角地区城市之间的效率值差异较大，该阶段大部分地区均为无效率，没有一个城市能持续保持效率值大于1。平均研发效率值排名前3位的城市分别为惠州(1.162)、深圳(1.082)、珠海(0.893)，后三位城市分别为肇庆(0.251)、中山(0.352)、佛山(0.607)。珠三角地区科技创新研发阶段总体水平比较稳定，研发阶段平均效率值在2013年达到谷值后有一定程度回升，波动幅度虽有明显变化，但总体来看处于合理范围内。

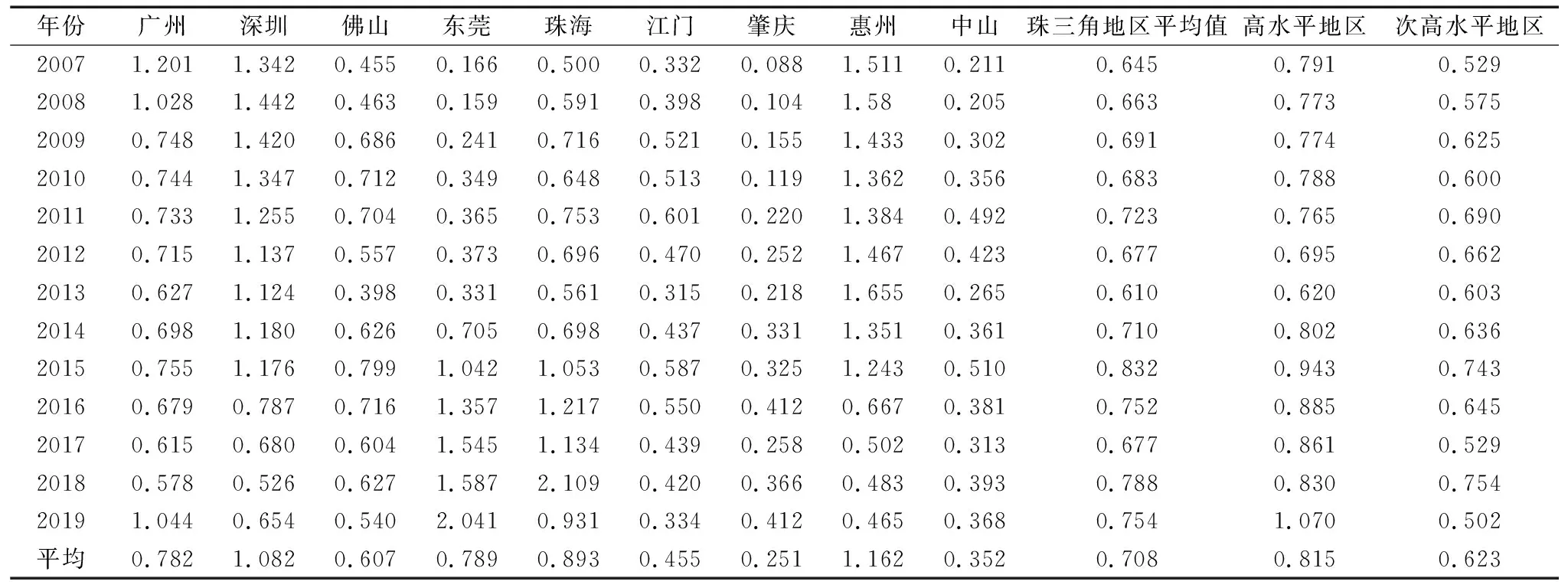
表2 2007—2019年珠三角城市科技创新研发阶段效率评价指数Tab.2 Efficiency evaluation index of scientific and technological innovation and R & D stage of cities in the Pearl River Delta from 2007 to 2019

高发展水平地区与次高发展水平地区研发阶段效率值具有显著差距，高水平地区研发阶段平均效率值比次高水平地区高0.192，两者之间效率差距在2013年之前不断缩小，在2013年接近相等之后又被迅速拉开并有扩大趋势。两类地区整体变化趋势与珠三角地区类似，效率值变动幅度均由平缓变得逐渐陡峭，区别在于2013年以前高发展水平地区效率值呈下降趋势，而次高水平地区则呈现缓中带增趋势。从图2可以看出，高水平地区效率值大于次高水平地区，因为高发展水平城市往往伴随着更高的科技研发效率。

图2 珠三角地区科技创新经济产出阶段效率评价指数变化趋势Fig.2 Change trend of efficiency evaluation index in the economic output stage of scientific and technological innovation in the Pearl River Delta

科技创新经济产出阶段具有非期望产出特征，加入3类非期望产出后测算的转换效率结果如表3所示。从中可见，相对于研发阶段效率，经济产出阶段除部分城市外都是有效的，平均效率值排名前3位的城市分别为深圳(1.612)、惠州(1.268)、广州(1.2)，后三位城市分别为珠海(0.666)、江门(0.797)和佛山(0.96)。在经济产出阶段，城市间差距比研发阶段更大，效率值最高的深圳比效率值最低的珠海高出将近1，说明城市经济水平和贸易环境对科技成果转化具有显著影响。

表3 2007—2019年珠三角城市科技创新经济产出阶段效率评价指数Tab.3 Efficiency evaluation index of scientific and technological innovation and economic output stage of cities in the Pearl River Delta from 2007 to 2019

2007—2019年，珠三角地区经济产出平均效率值为1.087，整体有效，平均效率变化趋势如图3所示。随着时间推移，珠三角地区效率值呈现轻微的倒U形变化特征。2013年之前，效率值变化呈上升趋势，之后每年虽有轻微下降，但变动幅度较小，极差为0.205。另外，高发展水平地区整体平均效率值高达1.233，次高水平地区仅有0.971，说明高发展水平地区与次高发展水平地区效率值差距较大。但随着时间推移，两者差距逐渐缩小，次高水平区域经济产出效率变化幅度明显增大，在2012年达到经济产出有效后基本维持在这一水平之上。与研发阶段类似，高发展水平地区在经济产出阶段效率值也更高。

图3 珠三角地区科技创新经济产出阶段效率评价指数变化趋势Fig.3 Change trend of efficiency evaluation index in the economic output stage of scientific and technological innovation in the Pearl River Delta

4 科技创新效率与经济韧性交互路径分析

4.1 指标构建

4.1.1 区域经济韧性评价指标

区域经济韧性测量方法主要包括以下两类：一类是 “一篮子”综合指标法，如使用层次分析法、熵权法等进行分析[27-28]；另一类是选取一个兼备敏感性和代表性的指标，用于反映区域对外部冲击的敏感程度[29-32]。本文借鉴Martin[14]的做法，选择单变量指标测算法，由于就业状况是最有可能受到冲击的指标，能反映一个地区的真实经济运行情况，因此本文重点对其进行探讨，具体计算公式如下：

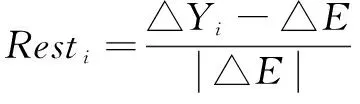
(3)

(4)

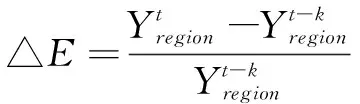
(5)

在公式(3)中，Resti代表i地区第t年的经济韧性；在公式(4)中，△Yi表示i地区从t-k年到t年Yi的变化率，本文选取地区就业人数作为Yi的观测值；同理，△E代表地区i所在经济区域region从t-k年到t年的Yregion变化率。本文设定k=1，Resti代表第t年的经济韧性。当i地区经济运行状况好于整体区域经济运行状况时，便认为该地区经济韧性较强。为直观考察时空差异并进行实证分析，使用指数化方式处理测量结果。

(6)

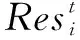
4.1.2 产业多样化评价指标

考虑到科技创新依赖于企业及区域经济活动的多样性[33]，会通过产业结构多样性分散外部冲击风险并增强区域经济韧性，因此本文加入相关多样化和非相关多样化两个指标，并采用孙晓华和柴玲玲[34]的熵值法进行测量，计算公式如下：

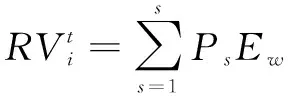
(7)

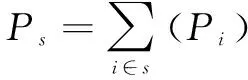
(8)

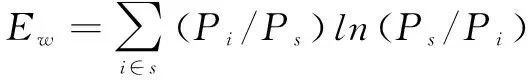
(9)

假设经济系统中存在s个大类部门，大类部门又可细分为n个小类部门(s≤n)。其中，RVti代表i地区第t年的产业相关多样化指数，数值越大，说明产业相关多样化程度越高；Ps、Pi分别代表第s个大类部门和第n个小类部门的就业份额，式(8)表示某大类部门就业比重之和是该部门下细分部门就业比重之和；Ew代表一大类部门内部各细分部门的多样化程度。

(10)

4.2 实证模型设定

利用非期望超效率SBM模型虽然可以直接测算投入冗余，但会将研究视角局限在投入变量上，因此本文选择Tobit模型进行回归分析，基本模型设定如下：

(11)

其中，Yit为因变量，代表科技创新两阶段效率值；Xit是由各种解释变量构成的矩阵，核心解释变量为区域经济韧性、区域产业相关多样化和非相关多样化；β为待估计系数，εit为误差项，本文假定其服从正态分布：εit～N(0，σ2)。

为更加全面和准确地考察外界因素对科技创新效率的影响，本文加入区域经济开放程度、区域教育经费支持、区域教育资源配置、金融发展规模和政府干预力度4个变量，分别选取当年实际使用外资金额(FDI)、教育费用支出占地方财政支出的比重、高等学校师生比、金融机构贷款余额和地方财政支出占GDP的比重作为观察指标。为消除量纲不一致可能带来的偏误，本文对变量进行对数化处理，因变量描述性统计结果如表4所示。

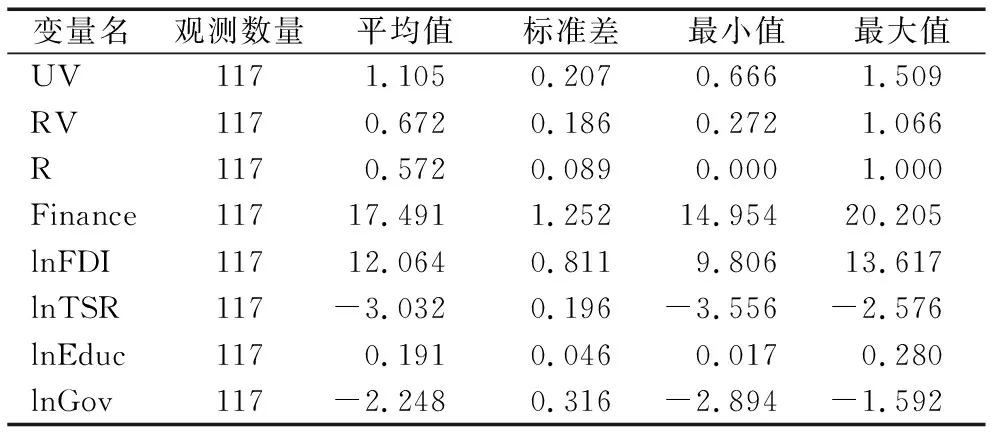
表4 因变量描述性统计结果Tab.4 Descriptive statistics of dependent variables

4.3 Tobit模型估计结果与内生性讨论

本文采用2007-2019年珠三角地区9个城市数据对变量进行检验，结果如表5所示。其中，在模型(1)和模型(2)中，因变量只包含区域经济韧性、产业相关多样化和非相关多样化；模型(3)～(6)加入控制变量，其中模型(5)、(6)进一步考虑地区和时间异质性，控制时间和地区固定效应，以提高估计系数的准确性。总体而言，区域经济韧性对科技创新第一阶段效率值具有显著正向影响，但第二阶段三类模型估计系数正负不一致，同时在10%显著性水平下不显著。产业相关多样化和非相关多样化也存在类似问题，但这是否说明除科技创新第一阶段外，区域经济韧性及产业多样化未对科技创新活动产生显著促进效果？本文认为，Tobit模型并不能完整反映科技创新活动、经济韧性与产业多样化之间的关系，由于三者之间存在交互，科技创新活动一方面能通过产业结构多样化将科技研发产出转换为经济效益，进而影响区域经济韧性；另一方面，科技创新活动的开展有赖于经济环境，经济韧性强的地区能提供稳定的研发环境和良好产业结构以供其开展科技研发与经济转换，使用Tobit模型可能存在内生性问题并导致系数估计结果有误，因此本文采用联立方程模型解决这一问题。

表5 Tobit模型实证结果Tab.5 Empirical results of Tobit model

4.4 联立方程组模型估计结果

从理论上讲，区域经济韧性影响科技创新每个阶段的产出效率；反过来，科技创新每个阶段的转换效率也会影响地区经济韧性。因此，本研究通过构建联立方程组考察区域经济韧性与科技创新两阶段转换效率的关系，具体公式如下：

式(12)为区域经济韧性方程，其中lnRit为i市在第t年的区域经济韧性，lnsbm1it、lnsbm2it分别代表i市在第t年科技创新研发阶段和经济转化阶段的效率值，lnRVit、lnUVit分别表示i市在第t年的产业相关多样化和非相关多样化程度，考虑到经济韧性可能存在时间关联，因此加入滞后一期的值；由于当期研发阶段效率受上一期经济产出阶段的影响，因此在式(13)科技创新第一阶段方程中加入lnsbm2it-1，反映第二阶段效率滞后一期的值；同理，科技创新第二阶段也受当期第一阶段的影响，因此加入当期第一阶段活动的效率值。

本文对两阶段效率值、经济韧性、产业多样化指数进行对数化处理，以降低量纲的影响，将左侧断尾效率值对数化后可以减少一定的误差。Tobit模型中的其它因变量被当作外生工具变量用在3SLS估计中，不直接出现在模型结果中(见表6)。

表6模型(1)结果表明，科技创新活动对经济韧性具有正向影响，但科技创新活动研发阶段和经济产出阶段对经济韧性的影响作用相反。其中，研发阶段对经济韧性有轻微抑制作用，但估计系数不显著；经济转换阶段在1%显著性水平上对经济韧性具有显著正向影响，该阶段效率值每增加1%，经济韧性将提升0.22%。考虑地区和时间固定效应后的估计结果如模型(4)所示，从中可见，无论是第一阶段还是第二阶段的效率值均在1%显著性水平上大于0，说明科技创新两阶段效率对经济韧性具有显著正向影响，无论是第一阶段还是第二阶段效率值每增加1%，经济韧性均能提高1%，这从侧面印证地区和时间异质性会影响估计结果。引入地区和时间虚拟变量能在一定程度上消除地区异质性的负面影响，因此本文采取固定效应估计模型。在区域经济韧性方程中，产业多样化类型和程度未直接对经济韧性产生显著影响，估计系数不显著，由此得出科技创新活动两阶段效率提升均有利于增强经济韧性的基本结论。

表6模型(2)、(5)和模型(3)、(6)分别为研发阶段效率与经济转换阶段效率估计系数结果。在科技创新研发阶段，产业相关多样化对该阶段效率起抑制作用，而非相关多样化则起促进作用，二者估计系数均在1%显著性水平上显著，而经济韧性估计系数为负且不显著。在控制地区和时间固定效应后，产业相关多样化和非相关多样化系数值未发生明显改变，而经济韧性估计系数为正且在1%检验水平上仍然显著，说明经济韧性对科技研发阶段效率具有正向影响，强经济韧性地区更能提供稳定的研发环境，进而提高该阶段产出效率。从产业多样化估计系数结果可以看出，非相关多样化数值每增加1%，研发阶段效率提高2.475%；而相关多样化系数值每上升1%，研发效率就将下降1.92%，两者估计系数均通过1%显著性水平检验。

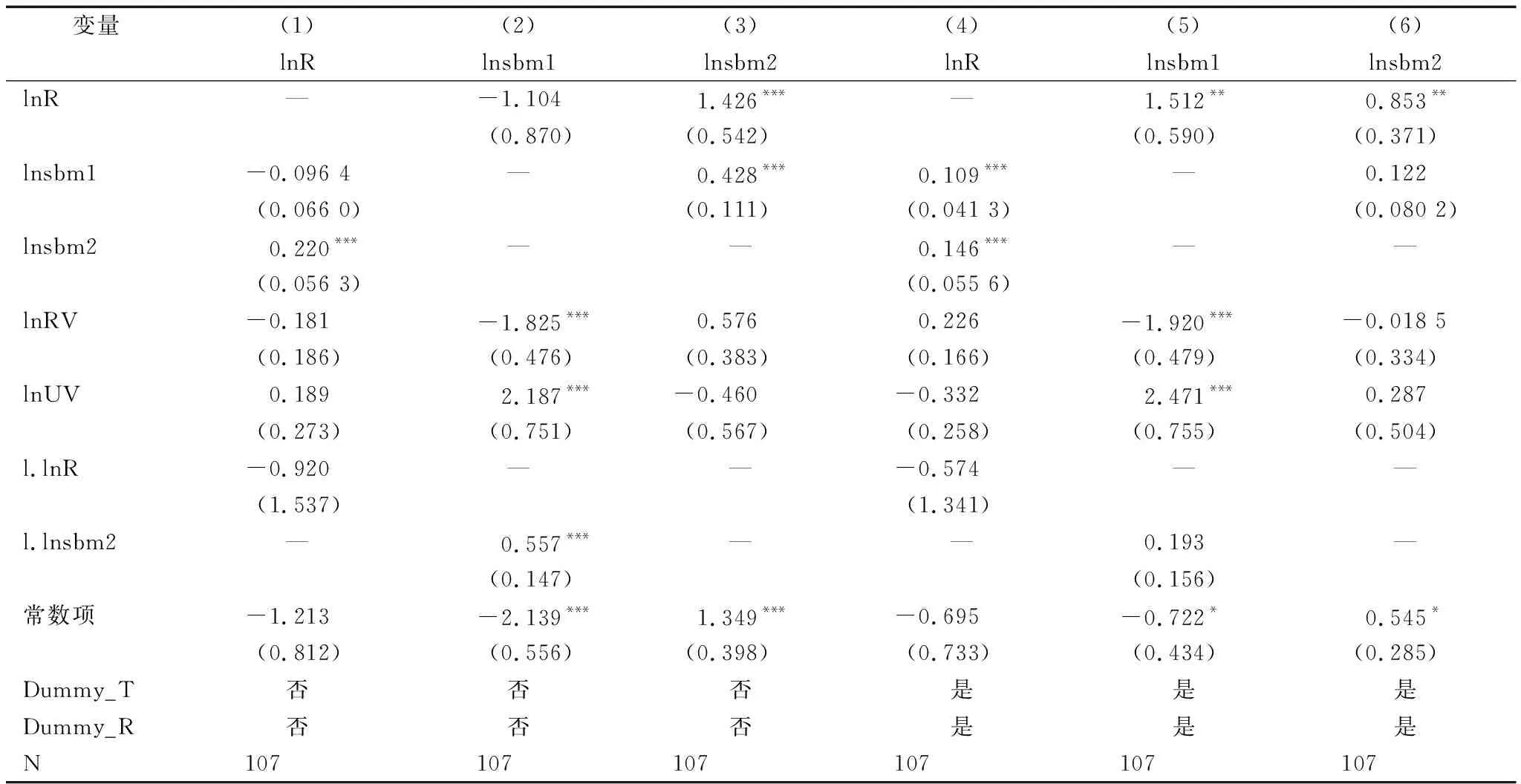
表6 联立方程组模型实证结果Tab.6 Empirical results of simultaneous equations model

本文认为,相关多样化会抑制研发阶段效率提升，非相关多样化反而会提升第一阶段效率值，这与主流观点相反。这是因为，珠三角地区是整个中国科技创新活动最为活跃也是科研创新水平最高的地区之一，相较于国内其它大部分地区，珠三角地区创新路径已经从产业内部创新跨越到应用范围更广、适用面更宽的产业间创新，属于一种跨产业、跨领域、跨平台交互创新，因此增加产业非相关多样化更能够提高现阶段珠三角地区科技创新研发水平。

在经济产出阶段，无论是否控制固定效应，区域经济韧性对经济产出均具有显著正向影响，在控制双向固定效应后，估计系数减少到0.853，但依然在5%显著性水平上对第二阶段效率起促进作用；当期研发阶段效率对第二阶段经济产出的估计系数也都为正，但在控制固定效应后系数变得不再显著，说明前一阶段研发结果对后一阶段存在一定程度的影响。在经济产出阶段方程中，产业多样化无显著影响。这是因为，当研发阶段结束后，研发成果转换只涉及单一行业内部出售和应用，产业多样化在该阶段并不能带来显著影响。

结合整个联立方程看，在控制地区和时间异质性后，产业多样化尽管没有对经济韧性产生显著影响，但通过科技创新活动影响区域经济韧性。从回归结果看，产业相关多样化对研发阶段具有抑制作用，而非相关多样化对研发阶段则具有促进作用；在经济产出阶段，尽管产业多样化估计系数不显著，但相关多样化和非相关多样化系数与第一阶段相同。结合3个决定方程可以发现，产业相关多样化会削弱地区经济韧性，而非相关多样化反而会增强地区经济韧性，这一结论符合韧性构建原理。即当地区产业结构特征高度相关时，尽管产业多样化会在一定程度上将外部冲击风险分散和转移到不同产业，但产业间强相关性反而会将外部风险分散路线固定，进而加大某一产业风险。而且，产业高度相关意味着当一个产业衰落时，与其相关联的一系列产业也会遭遇冲击，从而不利于区域经济韧性构建。相反，当地区产业结构特征非相关多样化程度较高时，即使一个产业受到巨大冲击，其它产业依然能够在保持自身功能的同时共同分担风险，以保持区域经济稳定。

5 结论与讨论

5.1 研究结论

本文以非期望超效率SBM模型测算珠三角地区2007—2019年的科技创新活动两阶段效率，分析两阶段效率值时空分布和变化趋势。以区域经济韧性和产业多样化为研究视角，探讨科技创新两阶段效率、经济韧性和产业多样化之间的关联，得出以下结论：

(1)珠三角地区科技研发阶段和经济产出阶段效率值存在显著差异，且在空间上存在着显著异质性。科技创新两阶段转换效率值较为平稳，但研发阶段系统效率值不高，而经济产出阶段则基本达到有效标准。时空异质性主要表现为：高发展水平地区往往拥有更高的科技研发和经济产出效率，在研发阶段效率值地区差异先缩小后又拉大，经济产出阶段则逐年缩小。

(2)科技创新两阶段效率与经济韧性存在双向因果关系，且存在一定的内生性问题。经济韧性可通过影响科技创新活动环境而对科技创新效率产生影响，科技创新效率也可通过提高地区科技创新水平、加快地区经济转型和推动产业结构升级，使地区更具有经济韧性，因此模型中存在一定程度的内生性问题。

(3)在考虑地区和时间异质性后，科技创新两阶段效率对经济韧性具有显著正向影响，经济韧性也能给两阶段效率提供支持，高经济韧性地区科技创新两阶段效率值更高。产业相关多样性会降低珠三角地区科技创新研发阶段效率，而非相关多样性则会提高该阶段产出效率。

(4)当科技创新活动处于不同研发水平时，其创新路径和创新内容并不会一成不变，研发阶段需要有技术的铺垫和支持。当一个地区整体处于低端创新阶段时，产业相关多样性能够节约创新成本，通过技术外溢和协同效应提高研发效率。但随着技术创新水平的不断提升，相关性强的创新成果趋于饱和，边际产出效应递减，从而降低研发阶段效率。因此，在高科技创新水平地区，相关部门在引导产业结构转型升级过程中应关注产业非相关多样化，开展跨部门跨领域融合创新。

(5)产业多样化虽然对经济韧性无直接显著影响，却可通过科技创新研发对经济韧性产生间接影响。产业高相关多样化会削弱地区经济韧性，当面临外部冲击时，风险固定传导路径会抵消产业多样化对风险的分散作用，让外部冲击向特定部门和产业传导，不利于地区经济韧性构建。相反，非相关多样化结构更能让外部冲击分散到各个产业，使各产业部门在可接受范围内承担风险并保持稳定，使地区更具有经济韧性。因此，相关政策部门不仅需要重视地区产业布局多样化，也需要考虑非相关产业发展，把握好两者之间的平衡，并根据地区发展水平和发展目标制定相应计划，做到因地制宜。

5.2 研究启示

珠三角地区科技创新两阶段效率状况带来如下启示：一方面，当前珠三角科技创新活动研发处于无效率阶段，相较于经济产出阶段，该阶段更应引起政府部门和企业重视，避免因为第一阶段无效率而“拖后腿”；另一方面，地区科技创新效率差异主要集中在第一阶段，并且差异值越来越大，为缓解地区效率不平衡，政府需要进行科技创新要素的合理配置。

5.3 不足与展望

本文存在如下不足：一是数据获取有限。由于科技创新活动指标没有完整的统计数据，所选取的替代性指标在一定程度上会影响结论的可靠性。二是科技创新效率、经济韧性、产业多样化及外界影响因素大多选取的是量化指标，缺乏对地区文化习俗、人文环境、政策执行效率和政府公信力等非量化指标的探讨。未来可从空间分布、空间集聚度等视角，将区域产业结构变化纳入科技创新与经济韧性交互作用中，分析三者之间的传导路径，并进行更为详细和深入的研究。