基于粒子群和遗传算法的面板堆石坝土石方调配研究

赵瑜， 贾政， 张建伟， 曹克磊， 陈传宇

(华北水利水电大学,河南 郑州 450046)

面板堆石坝具备良好的抗震性和透水性，施工导流方便，对河谷地质要求也不高，现已被普遍应用在大型水利工程建设中。但其施工条件复杂、挖填方量大，且料源众多，有时还需考虑施工过程中存在或可能产生的不确定性问题，规划与协调好土石方调配工作对于整个工程建设十分重要。

土石方调配问题普遍存在于路堤、场平、地下、土石坝等众多土建工程中，不同土建类型考虑问题的侧重点不同。当前对土石方调配主要围绕两个方面的问题进行研究：一是创建考虑具体工程特点的土石方调配模型；二是寻找更合适的算法对已有土石方调配方案进行优化。柳志新等[1]根据堆石坝施工过程中动态变化的特点，建立了对机械设备等资源进行优化的土石方调配模型；周厚贵等[2]对土石方调配研究工作进行了系统总结；陈秀铜等[3]、李晓伟等[4]、黄丙湖等[5]、王仁超等[6]分别使用改进粒子群算法、线性规划方法、蚁群算法、蒙特卡洛树算法对运算所得土石方优化方案进行了可行性研究。针对五岳抽水蓄能电站面板堆石坝复杂的施工条件，结合以上的研究成果，充分考虑各种不确定性因素[7]，建立适合工程需要的土石方调配模型，并分别采用粒子群和遗传算法对所建模型进行计算，以便得到贴合工程实际的土石方调配方案，实现对土石方调配方案的优化。

1 粒子群和遗传算法

Eberhart和Kennedy通过对鸟类捕食行为进行观察，创造了一种以群体协作和信息共享为思想的进化计算技术，称为粒子群算法(particle swarm optimization，PSO)。John Holland通过研究遗传学中自然选择过程，以适者生存为理念，提出了一种可以不断交叉和变异从而产生更优秀下一代的进化计算技术，称为遗传算法(genetic algorithm,GA)。

1.1 粒子群算法

假定有群体数量相同的未知鸟群，鸟群数量不小于1。先以其中一个鸟群为研究对象，不关注这个鸟群中每只鸟的高矮胖瘦，只关注它们在三维空间的位置及飞行速率和方向，鸟群被抽象为只有坐标点位置和速度的矢量。以Xin(k)表示粒子位置，以v表示速度。每个粒子先根据自身经验搜寻到当前最优目标(个体极值)，再通过互相交流经验确定当前群体目标(群体极值)，经过不断重复以上操作，直到满足预期目标，输出最优值，此为粒子群算法循环机理[8]。粒子群算法迭代公式如下：

Vin(k+1)=ωVin(k)+c1r1[Pin-Xin(k)]+

c2r2[Pg-Xin(k)]，
Xin(k+1)=Xin(k)+Vin(k+1)。

(1)

式中：ω为惯性权重；c1、c2为加速常数；r1、r2为随机数；Vin为粒子i飞行速度的n维分量;Pin为i粒子个体经过的最好位置;Pg为粒子群体经过的最好位置。

1.2 遗传算法

假定一个鸟群中有数量不少于1只的鸟。该鸟群中每一只鸟都具有不同的捕食能力，并会根据生物学规律产生具有不同捕食能力的下一代鸟群。鸟群中任何一只鸟都有可能发生遗传学变异，表现在鸟身体内部为染色体变异。每一只鸟身体内部的染色体在不断发生遗传、交叉和变异，子代鸟群和父代鸟群不断对比捕食能力，能力强的被认定为更适合生存，体现在数学应用上就是能更好地满足目标效果的群体更强。通过不断迭代更新出更适合生存的群体，这就是遗传算法的循环机理。染色体的交叉和变异是以一定的概率产生的，运用遗传算法程序时使用默认值即可满足大多数求解条件。

1.3 粒子群和遗传算法的特点

粒子群和遗传算法都基于对生物群体生存需求的研究，两者运算流程大体相同，都会随机初始化群体、并创建适应度评价，通过不断迭代来实现最终目标。迭代方式的差异使得两种算法各有优缺点。粒子群算法以粒子速度和位置的变化进行迭代[9]，遗传算法以染色体交叉、遗传、变异来进行迭代，共享信息机制的不同造成遗传算法全局寻优性能强，粒子群算法收敛速度快[10]。

2 土石方调配问题分析

2.1 影响土石方调配的因素

土石方调配工作贯穿面板堆石坝施工全过程。基于粒子群和遗传算法的土石方调配运算流程设计如图1所示。主要影响土石方调配的因素包括：①规划需要开挖的项目[11]，如坝基、库岸、导流工程等；②规划需要填筑的项目[12]，如坝体、道路、库内回填等；③具备开采和加工作用的料场及放置中转料和弃渣的堆场，它们的容量、位置的不同会影响调运单价，从而改变调配费用；④为土石料运输提供条件的器械和配套道路，合理的器械配套及道路布置可使材料运输通畅，利于施工，减少费用；⑤施工技术水平，水平越高，施工单位对各种土石料的利用越充分，可减少很多不必要的财力浪费。以上要素互相关联、相互约束，在时间和空间上也相互影响。在土石方调配过程中还应遵循料尽其用、有利上坝、经济合理等原则。

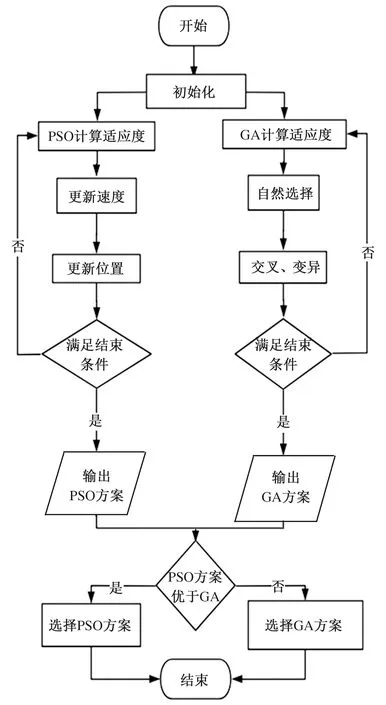
图1 土石方调配运算流程

2.2 土石方调配优化模型的构建

以调配费用最低为目标，确定目标函数：

(2)

式中：y为供料源；z为受料点；St为调配时段；Cyz为从供料源y到受料点z之间的费用系数；Xyz为从供料源y到受料点z之间的调配方量。

考虑施工管理水平、挖填进度要求、料场容量限制等实际情况，建立约束条件如下[13-16]。

1)填筑进度约束，约束条件如下：

(3)

式中:ATjSt为St时段填筑项目Tj的填筑总量;X为调配方量；XWiTjSt为St时段开挖项目Wi到填筑项目Tj的调配总量,i∈[1,nw];Zm为中转场，m∈[1,nz];Lk为料场，k∈[1,nl]。

2)开挖进度约束，约束条件如下：

(4)

式中:AWiSt为St时段开挖项目Wi开挖料的有效利用量；Tj为填筑项目，j∈[1,nt];Ql为弃渣场，l∈[1,nq]。

3)中转料场容量约束，约束条件如下：

(5)

式中：AZmSt为St时段初中转场Zm的料物堆存量；VZm为中转场Zm的容量。

4)中转料场出料约束，约束条件如下：

(6)

5)中转料场平衡约束，约束条件如下：

(7)

式中AZmSt+1为St+1时段初中转场Zm的料物堆存量。

6)中转场调配结束的零约束，约束条件如下：

(8)

7)弃渣场容量约束，约束条件如下：

(9)

式中VQl为弃渣场Ql的容量。

8)运输路径约束。运输路径约束反映挖、填、转、弃料场的使用规划，在某时段内，对于不可能运输路径取值为0，对于符合使用规划和设计规定的取实际运距。

9)非负约束。要求线性规划的所有变量为非负数，即:

XWiTjSt≥0，XWiZmSt≥0，

XWiQlSt≥0，XLkTjSt≥0，

XLkZmSt≥0，XZmTjSt≥0，

XLkQlSt≥0。

3 工程实例

3.1 工程概况

五岳抽水蓄能电站面板堆石坝工程主要有主坝、库岸、副坝和进/出水口建筑物构成。坝顶高程351.0 m，顶宽10.0 m，主坝和副坝坝顶中心线总长1 354.2 m。库底开挖线位于310.0 m高程处，岸坡顶高352.1 m。库岸分两级坡开挖，高程330.0 m处设一级马道，道宽2.0 m。大坝填筑分两期进行[17]，一期填筑于第2年3月6号开始至第3年5月28号结束，大坝所有断面填筑至高程300.0 m，共需完成填筑量432.14万m3，月平均填筑28.81万m3，二期填筑于第3年5月28号开始至第4年2月28号结束，大坝所有断面填筑至坝顶高程，共需完成填筑量281.52万m3，月平均填筑31.28万m3。

根据大坝石料平衡和砂石加工毛料平衡示意图规定，转存场在土石方调配开始前有23.91万m3存量，并在一期调配结束达到37.95万m3存量，二期10.67万m3土石参与厂房工程施工，转存场最大容量为130万m3；砂石加工系统在土石方调配开始前有19.72万m3存量，并在一期调配结束达到47.52万m3存量，二期41.29万m3土石参与厂房工程施工，砂石加工系统最大容量为85万m3；弃渣场在土石方调配开始前有95.41万m3土石存量，弃渣场最大容量为280万m3。厂房工程施工不在此次土石方调配研究范围。对于堆、砌石料，填筑方换算成需要量时考虑5%的损耗系数；混凝土骨料需要量考虑1.35%的加工损耗及1.05%的运输、施工损耗，其他加工料需要量考虑1.25%的加工损耗及1.05%的运输、施工损耗。具体挖填进度见表1。

表1 土石方挖填进度表 万m3

在施工过程中每个阶段所对应的土石方密度不一样，在开挖时是自然方，在坝上填筑时是实方，在计算过程中均折合为自然方(实方等于自然方与转换系数的积)。土石方的转换系数见表2。

表2 自然方与实方转换系数

根据工程特点及《水利水电工程施工机械台时费定额》将本次土石方工程调运单价初步确定如下：运输单价1.2元/(m3·km)；装车单价1元/m3；开挖单价2元/m3。以匹配矩阵显示的供料线路运距见表3。

表3 供料线路运距的匹配矩阵 km

3.2 土石方调配结果分析

分别采用两种不同算法对该面板堆石坝土石方调配模型进行运算，迭代寻优过程如图2所示。

在粒子群优化中，当鸟群距离食物位置无限稳定地趋近零，即认定所得方案最优。图2(a)中每一个蓝点代表一个历史最优土石方调配方案，其中施工一期迭代至199代停止，施工二期迭代至181代停止。经计算得土石方调配费用分别为808.36万元和576.05万元。在图2(b)中，每一个蓝点代表一个历史最优土石方调配方案对应费用。其中施工一期迭代至51代停止，施工二期迭代至131代停止，土石方调配费用分别为807.21万元和497.08万元。由两种算法所得方案中土石方流向的具体数据见表4和表5，评价方案优劣的主要数据见表6。表4、表5和表6中数据均以自然方表示。

图2 两种算法的迭代寻优过程图

续表 万m3

表4 粒子群算法所得土石方调配方案 万m3

表5 遗传算法所得土石方调配方案 万m3

表6 两种算法方案下可利用料调配成果统计

由表4和表5初步可知：由料源到填筑区的土石方流向以库岸向堆石区为主，库岸向转存场的次之，流向弃渣场的土石方量最多的料源来自库岸。因此，由库岸向各填筑区的土石方流向应是该面板堆石坝工程土石方调配研究的重点，施工管理过程中土石方调配的重心也应放在此处。

由表6可知：两种算法下垫层区和碎石铺盖区的直接上坝率等各项数据均相同；两种算法下堆石区的上坝总量均为过渡料区的近15.66倍。按表6中堆石区和过渡料区上坝总量所占比重对直接上坝率进行加权平均，得出粒子群算法方案的整体上坝率为89.60%，遗传算法方案的整体上坝率为91.29%，遗传算法方案整体上坝率较高。经计算得，采用遗传算法方案对土石方进行调配所需费用比粒子群算法方案的在施工一期节省1.15万元、在施工二期节省78.97万元，两期共节省80.12万元。

结合表4、表5和表6中土石方流向数据及两种算法下土石方调配费用可知：整体上坝率越高，土石方调配费用越低，则对于该面板堆石坝工程，使用遗传算法方案进行土石方调配更好。

4 结语

1)文中建立了适用工程特点的土石方调配模型，并采用粒子群和遗传算法分别计算得出两种可行性方案。相比粒子群算法，遗传算法所得方案整体上坝率更高，费用更低，更适合对该工程土石方进行调配。

2)影响土石方调配的因素众多，施工现场很难做到将土石方实际流向与方案数据精准吻合，如何调整方案数据的误差范围有待进一步研究。