Cooperative differential games guidance laws for multiple attackers against an active defense target

Fei LIU, Xiwng DONG,b,c,*, Qingdong LI, Zhng REN,b

a School of Automation Science and Electrical Engineering, Science and Technology on Aircraft Control Laboratory,Beihang University, Beijing 100083, China

b Beijing Advanced Innovation Center for Big Data and Brain Computing, Beihang University, Beijing 100083, China

c Key Laboratory of Dependable Service Computing in Cyber Physical Society, Ministry of Education of China, Chongqing University, Chongqing 400044, China

KEYWORDS Active defense;Cooperative guidance;Differential games;Minimum effort optimization;Relative intercept angle

Abstract This paper is concerned with a scenario of multiple attackers trying to intercept a target with active defense.Three types of agents are considered in the guidance:The multiple attackers,the target and the defender,where the attackers aim to pursuit the target from different directions and evade from the defender simultaneously.The guidance engagement is formulated in the framework of a zero-sum two-person differential game between the two opposing teams,such that the measurements on the maneuver of the target or estimations on the defending strategy of the defender can be absent.Cooperation of the attackers resides in two aspects:redundant interception under the threat of the defender and the relative intercept geometry with the target. The miss distances, the relative intercept angle errors and the costs of the agents are combined into a single performance index of the game. Such formulation enables a unitary approach to the design of guidance laws for the agents. To minimize the control efforts and miss distances for the attackers, an optimization method is proposed to find the best anticipated miss distances to the defender under the constraint that the defender is endowed with a capture radius.Numerical simulations with two cases are conducted to illustrate the effectiveness of the proposed cooperative guidance law.

1. Introduction

The active target defense problem has received special interests in the aerospace guidance domain since it was firstly proposed in Ref. 1,2. In typical active defense scenarios, three types of agents are included: the target, the defender and the attacker.The attacker is guided to intercept the target while the defender endeavors to protect the target that strives to avoid the interception.Such problem introduces important and interesting challenges in the attack-defense confrontation scenarios,as pursuit and evasion objectives of the two adversaries, namely the attacker and the target-defender team, are combined in one system. Compared with the well-studied multi-agent control problems, it is an intellectual dynamic game process involving smart strategies of the three agents and has become a mainstream defense approach from the practical application point of view,such as high-value asset protectionsand antimissile defense missions.

(1) Motivation and presentation. In practical applications,for a high-value target, multiple missiles are often launched to ensure the saturation of the target’s defense or improve the success rate of interception. To prevent from being intercepted,the target usually launches a defender with some lethal area to destroy the threat(s). Normally, the target cooperates with the defender, where the target may perform elaborately designed maneuver to lure the attacker into an adverse situation and the defender finishes the interception more easily. In this sense, the attacker is at a disadvantage if the target is maneuvering. If more than one attacker is considered, such disadvantage could be greatly reduced. To coordinate the guidance of the multiple attackers,some cooperative strategies must be designed to confront the target-defender and the performance of the group would exceed the sum of one-on-one guidance performance of the attackers. In this paper, a small number of attackers aim to evade from the defender and intercept the target simultaneously. Notably, it is unadvisable to assign one attacker to destroy the defender because of limited resources, and it would consume the attackers and reduce the interception probability of the target. The attackers would endeavor to bypass the defender.Cooperation of the attackers are designed to reach the target with relative intercept geometry to enclose the target and benefit the observability. Moreover, to deal with the cooperation strategies of the target and defender, the differential games theory is introduced in the design of the cooperative guidance law. Such approach guarantees the lower limit of the attackers’ performance by countering the efforts of the target-defender.

Motivated by the facts stated above,this paper investigates the problem of cooperative guidance against an active defense target for imposing a relative intercept angle. Firstly, the linearized kinematics in the endgame phase is introduced and the cooperative guidance problem is formulated in differential games framework, where the objectives of the attackers and the control efforts of the adversaries are considered.Secondly,optimal solution to the cooperative guidance problem is provided by solving the differential games for the saddle point strategies. The guidance laws obtained enable the attackers to cooperatively intercept the target while maximizing the distance with the defender simultaneously. Thirdly, a second stage optimization problem is designed to obtain the desired miss distances with the defenders by minimizing the cost of the attackers. In order to reduce the computational effort,the feasible set of the optimization is simplified and the simplification method is justified.

(2) Related works. A scenario similar to the active target defense problem is the classical pursuit-evasion problem that involves two agents, the pursuer and the evader. Issacs firstly systematically studied the problem and proposed the theory of differential games.Thereafter,massive results in the guidance field are proposed in the framework of differential games theory. Remarkably, a multi-player pursuit-evasion scenario where multiple pursuers cooperate to capture a superior evader was studied in Ref. 19. Due to advances in the field of artificial intelligence, instead of using the methodology of differential games or optimal control, authors of Ref. 19 solved the cooperative pursuit problem in complex uncertain environments based on reinforcement learning, adopting distributed actor and critic networks to separately model the control strategies and value functions in the game.

Compared with the pursuit-evasion problem, the scenario of active defense introduces an extra agent, the defender, and thus complicates the design of the strategies of the agents.To reduce the complexity of the solution,it was formerly studied under the assumption that the attacker implements a known guidance strategy such as proportional guidance law. Therefore, the active defense problem is reduced to a one-sided optimal control problem to obtain the strategies for the target and the defender. Different from optimalcontrol-based methods, authors in Ref. 22 tackled this problem based on geometrical information of the target’s Line of Sight (LOS) and LOS rate, then the defender was capable of protect the target when the triangle formed by the three agents collapses to a line. The cooperative guidance laws for the target-defender team were proposed in Ref. 23 by converting the guidance problem into a two-input-two-output control problem subjected to terminal constraints and system constraints. An advantage for the guidance law in Ref. 22-23 is that no prior knowledge of the interception guidance law for the attacker is needed. Similar to Ref. 19, a reinforcementlearning-based method was adopted in Ref.24 to find the optimal launch time for the defender and the optimal bang-bang maneuver at each decision time for the target. The literatures referred above mainly focus on the cooperative strategies of the target-defender team.From the perspective of the attacker,if the cooperation strategies of the target-defender team are available,the optimal strategy for the attacker can be designed in the same optimal-control-based formulation. And in Ref.25, optimal guidance algorithms for both the attacker and the target-defender were proposed separately.

If the strategies of the attacker and target-defender are unknown to each other, which is reasonable in reality, the guidance strategies of the agents can be approached via differential games. Generally, the three-player game is transformed into a two-player game by grouping the cooperative players:The target and the defender.The work in Ref.27 investigated the case where the defender possessed a capture radius and obtained the analytical solution to the active target defense differential game.The authors of Ref.27 further studied the problem and provided a completed, closed form solution of the active target defense differential games in Ref.28.It was shown that the value function of the game was continuous and continuously differentiable over the target’s escape set.Note that the admissible controls in Refs. 27,28 are given in the form of instantaneous heading angles. Considering the dynamics of the heading angle, the attacker’s feasible region in the Attacker-Target (AT) engagement and infeasible region in the Attacker-Defender (AD) engagement were derived by one-to-one optimal guidance laws, respectively, in Ref.29.The guidance law for the attacker was divided into three phases: pursuit for the target until reaching the boundary of the infeasible region, evasion form the defender until the end of attacker-defender engagement and pursuit for the target by optimal guidance law. Analogous to Ref.29, the guidance problem for an interceptor against a ballistic missile with active defense was investigated in Ref.30 by switching the guidance strategies obtained in the AD and AT engagements respectively, where the zero-effort distance between the attacker and the defender was chosen as the key switching signal.Based on norm differential game strategy and linear quadratic differential game strategy, guidance laws for adversaries in a two-on-two engagement were proposed in Ref.31, where the interceptor is required to capture the spacecraft and evade from the defender with the aid of the protector.

Most of the aforementioned literaturesconsidered the active defense problem with one attacker.For multiple attackers, cooperative guidance problems have been studied extensively. Based on single impact-angle constrained or impact-time constrained guidance laws, cooperative guidance problems were addressed through impact-angle coordinationor impact-time coordination. Instead of imposing specific impact angle constraint, Ref.38 dealt with the explicit cooperative guidance problem in the presence of relative intercept angle constraint and Ref.39 obtained the guidance laws for the interceptors in the framework of zero-sum two-player differential game. The cooperative guidance law with relative intercept angle constraint guarantees the multiple missiles to intercept the target from various directions,and requires lower control effort than those guidance laws enforcing one-on-one preselected intercept angle. However, few researches on cooperative guidance consider the case of an active defense target.To the best of our knowledge, the problem that multiple attackers cooperate to intercept a target with a defender is still open.

Compared with the existing literatures, the main contributions of this paper have three aspects.Firstly,cooperative guidance laws for multiple attackers against an active defense target are proposed, where the attackers are enforced with relative angular geometry constraint at intercept. The guidance problem considered in this paper is a combination of cooperative guidance and active target defense problem. This problem can be deemed as a continuation and extension of the cooperative guidance in Ref.39.On the other hand,it is also a scenario of active target defense problem with more than one attacker involved, which is absent in most literature referred above in this domain. The proposed guidance law enables the attackers to simultaneously evade the defender and pursue the target with relative intercept angle constraint. Secondly,the problem is formulated in the differential game framework and saddle point solution to the game is obtained, with no information about the control strategies of the target/defender needed. In this paper, the cooperative guidance against the active defense target is analyzed in one differential games framework, which is a game of two groups: The attackers and the target/defender. Therefore, cooperation of the attackers and the target/defender are both considered in the guidance strategy design. In Refs. 29,30, the guidance law for a single attacker was derived via two separate one-on-one differential games, namely the attacker-target engagement and attackerdefender engagement, where no direct connection between the evasion from the defender and pursuit for the target is established in the game.Thirdly,since the defender is endowed with a lethality region, a cost function for the group of attackers is designed and an optimization method is proposed to determine the optimal zero-effort miss distances of all the attackers with respect to the defender.In Refs.21,25,a special function named dead-zone function is introduced in the guidance law to evade from a defender with lethality region. However, it is hard to obtain the analytical expression of the generalized dead-zone function when the number of attackers grows and the computational effort would increase exponentially to obtain a numerical solution. The method proposed in this paper greatly reduces the computational effort by filtering the optimization feasible region and selecting the best subset.

The remainder of the paper is arranged as below. The engagement between the multiple attackers and the active defense target is illustrated in Section 2. Besides, the cooperative differential games formulation is presented. In Section 3,cooperative guidance laws for the agents are derived in the framework of differential games. A second stage optimization to obtain the desired miss distances in the AD engagement is presented in Section 4.Numerical simulations are given in Section 5, followed by the concluding remarks in Section 6.

2. Problem formulation

The planar engagement of multiple attackers and a target in the presence of a defender is considered. The attackers aim to intercept the target by imposing relative intercept angles while escaping from the defender. The entities in this engagement scenario are assumed to be point mass vehicles.

2.1. Nonlinear kinematics

In this subsection, the nonlinear kinematics of the multiple attackers-defender-target in the planar engagement is introduced.The engagement between the attackers and the defender is denoted as AD, and the engagement between the attackers and the target is denoted as AT.

The endgame geometry is shown in Fig.1,where the Cartesian inertial coordinate system is given by X-O-Y. Variables associated with the ith attacker, the defender and the target are denoted by additional subscripts i, D and T, respectively.The velocity, acceleration and heading angle of the engagement entities are denoted by V, u and γ, respectively. It is assumed that the velocities of the entities are constant, therefore only the lateral accelerations normal to the speed are considered. The relative range between the ith attacker and the target/defender is denoted by ρ, k=T or D. Similarly, the angle between the ith attacker-to-target/defender line of sight and the Xaxis is denoted by λ.The kinematics of the engagement between the ith attacker and the target in a polar coordinate system is given bywhere the subscripts representing the index of the attackers,the defender and the target are dropped for simplicity.

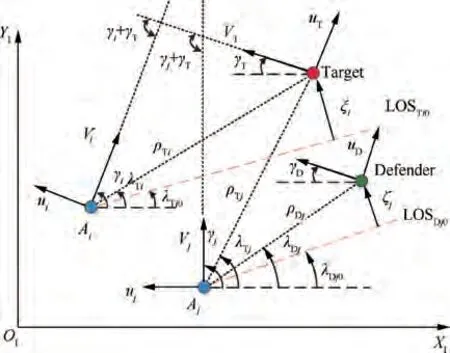
Fig. 1 Planar engagement geometry.

The intercept angles of the ith and jth attacker against the target are γ+γand γ+γ, respectively. The relative intercept angle refers to the difference between γ+γand γ+γfrom the target’s perspective. If the interceptions of the two attackers occur simultaneously, the relative intercept angle is calculated as γ-γ. Otherwise, the concept of relative intercept angle may lose meaning,but the attackers can still achieve a better tracking of the target by means of observability enhancement from different directions.

2.2. Linearized kinematics for cooperative guidance law derivation

The cooperative guidance laws for the attackers are derived based on linearization of the engagement kinematics. Usually,in the endgame,the deviations from the initial collision geometry to the current state is small, and the linearization brings little error. In some cases, if the target possesses large maneuverability or the initial scenario varies a lot from the collision triangle, then one can resort to extended linearization method and the linearization can be done at each time step.

Under the assumption of near collision course geometry,the linearization for the kinematic model of ith attacker is conducted at the initial attacker-to-target/defender line of sight,denoted by LOSand LOS, respectively. The relative displacement between the ith attacker and the target, normal to LOS, is denoted by ξ, and that between the ith attacker and the defender, normal to LOS, is denoted by ς.

Since the guidance to the target and the evasion from the defender are performed by employing the relative displacements ξand ς,it is natural to work with the accelerations that are normal to the initial line of the sights,which are obtained as

In the cooperative guidance of the attackers, it is also required that the attackers intercept the target by imposing different intercept angles.

2.3. Performance index of the cooperative differential games

In the attackers-target-defender scenario, the success of guidance mission is that the attackers achieve large miss distances in the AD evasion engagement and zero miss distances in the AT guidance engagement, along with the relative intercept angle requirements. The former miss distances are determined by the radius of lethality region R of the defender,where the following conditions should be satisfied:

Remark 1. The adversaries including the multiple attackers and the target-defender team constitute players of a zero-sum twoperson game. Cooperative guidance formulation in the framework of differential game requires no knowledge of the control strategies of the target and the defender,which has an advantage over the optimal-control-based methods that proceed with perfect information about the guidance strategies of the target-defender.The performance index of the game enforces cooperation between the multiple attackers, so as the target-defender team.The cooperation of the attackers is achieved in response to the target-defender strategies. Furthermore, the relative geometry requirement coordinates the trajectories of the attackers without assigning specific intercept angles.

3. Guidance law derivation

In this section, the optimal guidance laws for the agents that satisfy the saddle point of the differential game are derived.The original dynamics of the engagement motion is firstly transformed by order reduction technique based on its homogeneous solution. Then a two-side optimization is conducted to obtain the saddle point solutions of the differential game that is governed by the order-reduced engagement dynamics.

3.1. Order reduction

In the attackers-target-defender engagement scenario, the attackers are desired to escape from the defender and intercept the target with relative intercept angles. Therefore, the zeroeffort miss transformation is performed in both the AD and AT engagements, while the zero-effort angle transformation exists only in the latter engagement.

The order-reduced variable associated with the ith attacker is defined as

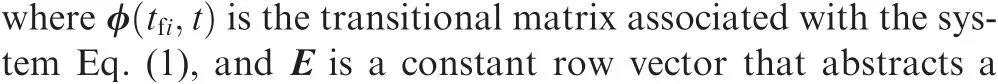
where 1（t-t） and 1（t-t） are step functions as defined above.

In the case of multiple attackers, even if the defender is initially located between the attackers and the target, it is probably that some attackers would be out of the reachable region of the defender. An attacker indexed as i would focus on intercepting the target without considering the threat of the defender if t≤t. To deal with this situation, the dynamics of the ZEMD is revised, by introducing an indicator reflecting the comparison between the AD and AT terminal time, as

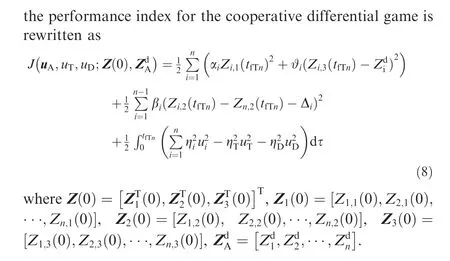
Remark 2. By means of the order-reduction transformation,the order of the original problem is reduced from 5n to 3n,where only the variables related with the control objectives are selected.Moreover, the other states in the dynamics of the engagement,which are not considered in the performance index,would not be regulated by the optimal strategies of the game.If the differential game is solved in the original problem formulation,all the states shall be stabilized and converge to some values,but such solution is superfluous to the guidance and evasion objectives.

3.2. Solution of the differential game

where t- and t+ represent the time before and after t,and so do t- and t+, and N, N, Nare interior constraints on the transformed states at intermediate time.

Since there are no constraints on the interior and boundary points, i.e. N=0（j=1，2，3）, then one gets from Eq. (11)that

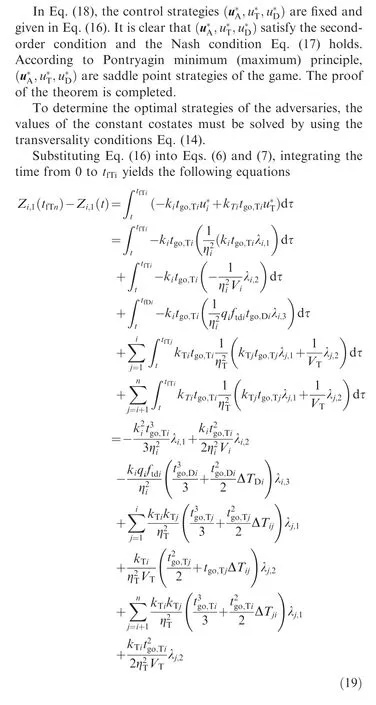
Remark 3. From Eq. (26), the proposed optimal guidance law for the attackers can be deemed as a classical proportional guidance law with extra terms. The first term in Eq. (26)integrates the ZEMT and ZEAT of the attackers because the cooperation of interception imposing relative intercept angles in the game needs the information of the other attackers. The second term is to generate the maneuver to avoid the interception of the defender.The optimal control strategies of the target and the defender counteract the guidance effort of the attackers with respect to the designed performance index.

4.Second-stage optimization for the desired miss distances in the AD engagement

4.1. Design of the optimization problem

4.2. Feasible set simplification of the optimization

Remark 4. The set S is a union of n unconnected convex domains. If there are n interceptors, the set S consists of 2convex sets and the optimal solution can be obtained by comparing the minimum solutions in each convex set. However,if n gets larger, the computational effort could be unacceptable.In Ref.25, the concept of dead-zone function is introduced to represent the optimal solution and the analytical expression of the one-dimensional dead-zone function is given explicitly in accordance to one interceptor. However, if the number of interceptors is two or more, the higher-dimensional dead-zone function is very complicated and can only be obtained through detailed discussions on every possible case.

To avoid such computation explosion, we choose two typical feasible subsets,over which numerical convex optimization algorithms, such as prime-dual interior point method, can be implemented to find the suboptimal solution rapidly.The computation complexity will be reduced from O（2） to O（n）. The two subsets are given as

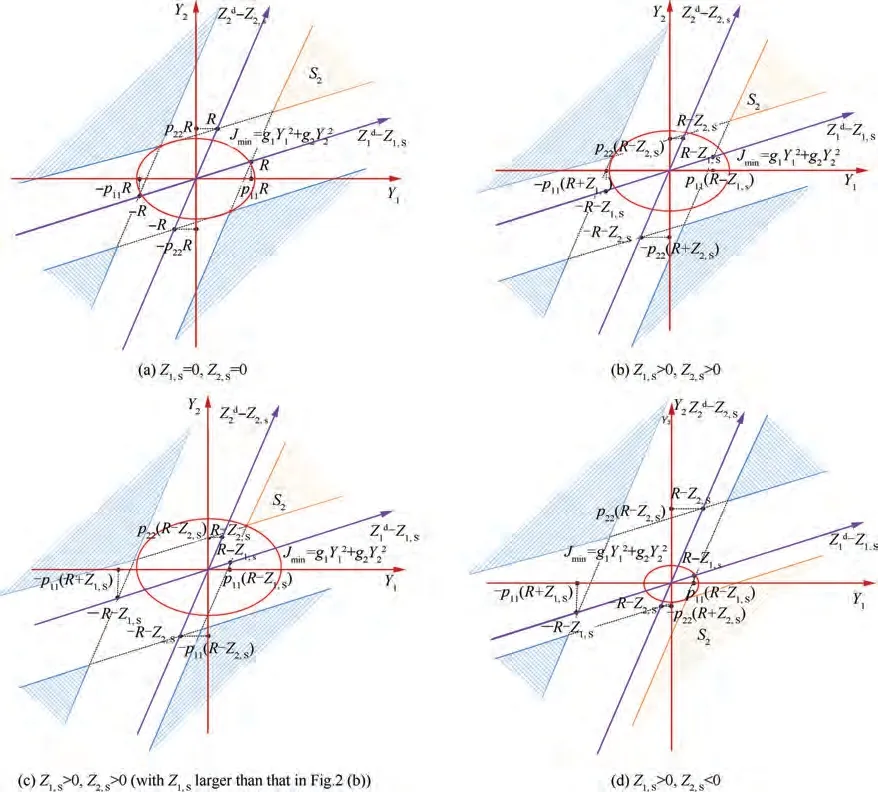
Fig. 2 Objective function and the feasible sets of the optimization.

Remark 5. It is difficult to obtain the analytical solution of the second-stage optimization as expounded in the above.Therefore,the selection of the subset of the original feasible set is a tradeoff between computation complexity and optimization performance.If the number of attackers is large,efficient computation method is necessary since the attackers must obtain the appropriate desired miss distances with the defender to feed the optimal guidance laws every time step to act rapidly, meantime saving energy and avoiding interception. And such subset selection criterion proposed in this paper is illustrated to having a better optimization result in most cases and verification is given in the numerical examples.

Remark 6. Although the suboptimal desired miss distances can be found by the proposed optimization method, it would be beyond the capability of the attackers to actually achieve the designed miss distances, if the radius of lethality region is very large or the defender stays close enough to the target. In these cases, it is impossible for the attackers to bypass the defender.The defender must be destroyed first and the problem would degrade to a cooperative guidance problem. The design of the‘‘first-strike” strategy is out of the scope of the paper and can be considered in future works on multiple missile confrontation problems.

5. Numerical simulation

In this section, the performance of the proposed guidance law is investigated in two active defense scenarios, where the nonlinear dynamics governs the motion of the entities in the simulation.

The first scenario is that the defender aims to directly intercept one of the attackers and the rest of the attackers are neglected. Therefore, the target would be exposed to the risk of interception by the free attackers.However,such dangerous situation is relieved to some extent by the fact that the attackers lack the information of the explicit target of the defender.

The second scenario is conceived based on and slightly more complicated than the first one.In this scenario,the defender at the outset employs the accompanying flight mode by maintaining a small distance with the target and being located in the collision course of the attackers. A threat identification zone is attached with and centered at the target, where any attacker firstly enters the threat identification zone will be target of the defender. Once the defender decides to intercept an attacker, the second scenario degrades into the first one.

The two scenarios involve three attackers,one defender and one target.The defender applies the typical proportional guidance law and the target performs a constant maneuver. The radius of the lethality region of the defender is known to the attackers, while the radius of the threat identification zone is private to the target-defender team and not accessible to the attackers. In the simulation, the adversaries are assumed to have first order actuator dynamics and a control saturation.The general fixed parameters in the engagement scenarios and the guidance laws are listed in Table 1.

5.1. Scenario 1

In this subsection, the performance of the proposed guidance law in the first active defense scenario as depicted above is investigated. The initial range between the attackers and the target is 3000 m, and the initial attackers-defender range is 2000 m. In the engagement, a relative intercept angle of 0.2 rad between the attackers against the target is enforced.The radius of the lethality region of the defender is given as R=20 m. Weights in the performance index of the cooperative differential games are chosen to be α=10, β=10,γ=10, η=1, η=3, η=3.

The trajectories and control inputs of entities in the engagement are presented in Fig. 3 and Fig. 4, respectively. For the attackers, the cooperative guidance consists of two phases.In the first phase,the attackers mainly concentrate on the evasion from the defender. The defender anticipates to intercept Attacker 2 at 2.82 s. However, due to the relative positions between the attackers and the defender, two of the attackers,namely Attacker 1 and Attacker 2, are in an adverse circumstance and under the threat of being intercepted. Since theattackers lack the knowledge of which of them is the target of the defender, both Attacker 1 and Attacker 2 detect the approaching of the defender and perform evasion maneuvers as seen from Fig. 4. Moreover, although the guidance laws of the attackers use no information of the acceleration of the defender, Attacker 2, which is the target of the defender, performs the maneuver ahead of the defender.When the guidance control saturation occurs, the control input of Attacker 2 and the defender are synchronized until the control of Attacker 2 is saturated, which means the defender cannot achieve more advantage in the AD engagement. This property is brought by the fact that the guidance laws for the attackers are derived based on the differential game solutions with no assumptions or reliance on the guidance strategies of the defender.

Table 1 Parameters in the engagement scenarios.

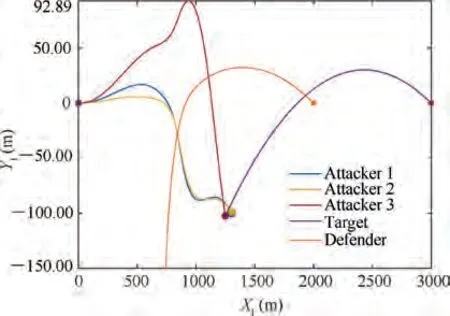
Fig. 3 Scenario 1: Trajectories of entities in the engagement(R=20 m).

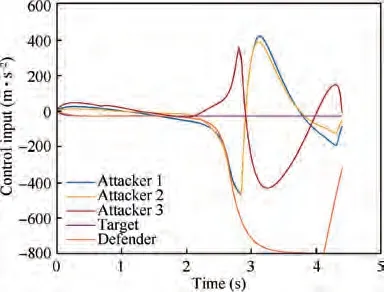
Fig. 4 Scenario 1: Control input of entities in the engagement(R=20 m).

When the defender passes the attackers,the attackers enter the second phase of the guidance and focus on the interception of the target with relative intercept angle constraint, which engenders the jump of the control inputs of the attackers.The profiles of ZEMT and ZEAT are presented in Fig. 5.Before the extrication from the entanglement with the defender, the ZEMT of the attackers continues to soar. Nevertheless, once the AD engagement ends, ZEMT of the attackers rapidly converge to values near zero (0.31 m, 0.01 m and 0.23 m, respectively). Meanwhile, relative intercept angles between the attackers are achieved with a relatively acceptable error, whose values are 0.15 rad and 0.25 rad comparing with the requirement of 0.2 rad.In guidance problems,the precision of the actual relative intercept angle performance is less important than the miss distance, and the gap can be reduced by increasing the corresponding weight in the performance index,where the relative values of the weights represent the relative importance of different control objectives.

Fig. 5 Scenario 1: ZEMT and ZEAT profiles in the engagement (R=20 m).

The profiles of ZEMD and the optimal desired ZEMD are presented in Fig. 6. At the end of the AD engagement, the ZEMD of the Attacker 1 and Attacker 2 are close to the radius of the lethality region of the defender.The guidance law regulates the curves of ZEMD of Attacker 1 and Attacker 2 to the boundary of safety region which is guided by the curves of suboptimal desired ZEMD. After the defender passes the attackers, the ZEMD are meant to approach the infinite. To prevent the singularity of the algorithm, a bound between-500 m and 500 m is set.In this case,the ZEMD of the attackers are equal to the suboptimal desired ZEMD. The part of maneuvers generated by the guidance laws to evade from the defender would no more exist and such a bound design has no adverse effects on the algorithm.

To evaluate the impact of radius of lethality region on the guidance engagements, simulations are also performed with R=10 m and R=30 m, respectively, while the other conditions remain the same. The trajectories in these two cases are shown in Fig. 7. The trajectories in Fig. 7(a) are similar to those in Fig. 3. Comparing Fig. 7(b) with Fig. 3 and Fig. 7(a),due to the expansion of the lethality region of the defender,both Attacker 1 and Attacker 2 maneuvers extremely to evade from the defender, whereas Attacker 3 neglects the defender and directly intercepts the target. It can be concluded that a larger lethality region of the defender can drive more attackers away from the target and a smaller lethality region reduces the threat of the defender.

The optimal desired ZEMD is obtained by the second-stage optimization of a cost function defined in Section 4. The cost function represents the combined control objectives of miss distance for the target,the relative intercept angle and the total control effort of the attackers. The profiles of the optimized cost in the engagements under three cases of radius of lethality region are presented in Fig. 8. Before the end of the AD engagement, the cost for the attackers continues to rise on account of the increasingly competitive confrontation with the defender. In fact, the cost would be nearly approaching infinite at the end of the AD engagement, hence a boundary of 10is added to the profiles in the figure for a better presentation.Because the saturation of the control inputs of the entities is not modeled in the cooperative differential games, the attackers would not expect a bound of the control signals generated by the guidance law and the cost is expected to rise continuously as reflected in Fig. 8. Once the AD engagement terminates,the cost experiences a sharp reduction and is gradually down to zero when the target is intercepted.Moreover,if the radius of the lethality region becomes larger,the cost of the attackers increases more rapidly since the attackers need larger maneuver to change their courses and complete the missions,however, such tendency fails to be valid at the beginning of the engagement since the threat of the defender is small.

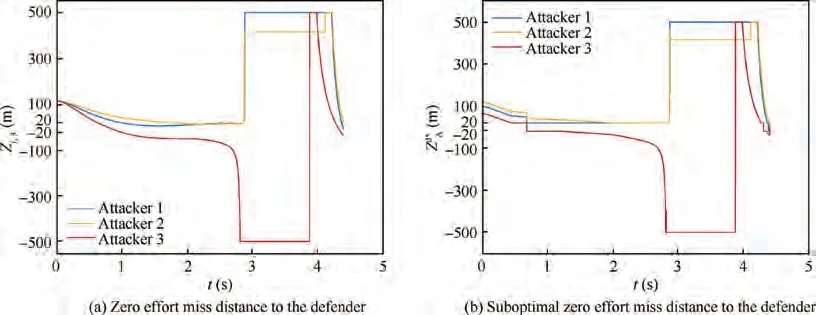
Fig. 6 Scenario 1: Actual and suboptimal zero effort miss distance against the defender in the engagement (R=20 m).

Fig. 7 Scenario 1: Trajectories of entities in the engagement with different values of R

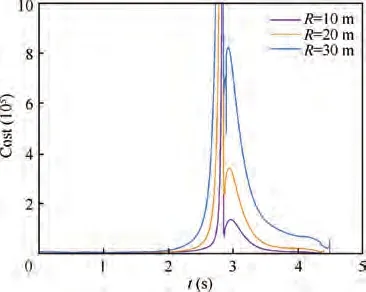
Fig.8 Scenario 1:Total cost of the attackers in the second-stage optimization

5.2. Scenario 2

In this subsection, the performance of the proposed guidance law in the second active defense scenario is investigated.In scenario 2,the initial attackers-target range is 3000 m and the initial defender-target range is 300 m. The initial heading angles for the defender and the target are zero. The other other conditions are the same as those in scenario 1.As a matter of fact,the defender and the target are supposed to have the same velocity to maintain the accompanying fly mode and the change of the relative defender-target range is small during the endgame. The accompanying flight for the defender is achieved by using a simple guidance law of pure pursuit against a virtual target.

Fig. 9 Scenario 2: Trajectories of entities in the engagement(R=20 m)

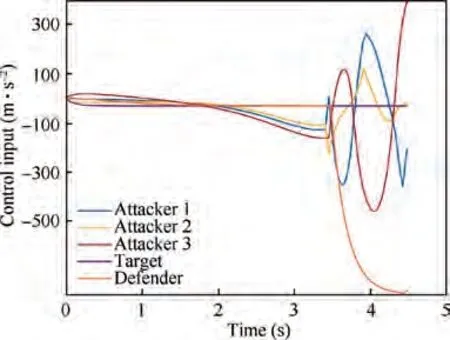
Fig. 10 Scenario 2: Control input of entities in the engagement(R=20 m)

The engagement trajectories of scenario 2 are illustrated in Fig. 9. Also, the control inputs of the entities in the endgame are presented in Fig.10.Before the target detects the attackers,the acceleration of the defender stays at a low level and synchronizes with that of the target. As the attackers enter the threat identification zone of the target, the defender instantaneously starts the interception at 3.48 s.Meantime,the attackers perceive the defender as an obstacle before the target and also perform high maneuver to bypass the defender.As shown in Fig.10,the control inputs of the attackers go through a very rapid change with large amplitude when approaching the defender and the target. The trajectories of the attackers at the endgame are severely interfered by the defender.

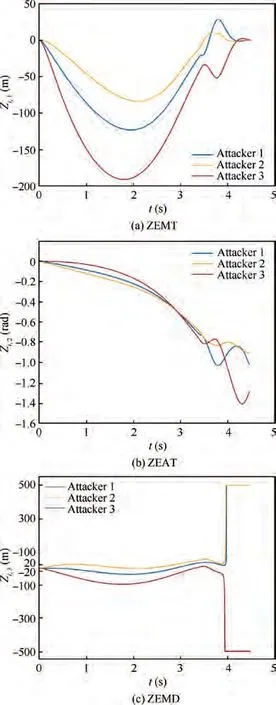
Fig. 11 Scenario 2: ZEMT, ZEAT and ZEMD profiles in the engagement (R=20 m)

The profiles of ZEMT,ZEAT and ZEMD are presented in Fig. 11. Although the attackers are hindered by the defender,the interception with relative angle constraint is completed.The miss distances between the attackers and the target are 0.32 m, 0.22 m and 0.10 m. The relative intercept angles between the attackers are 0.27 rad and 0.12 rad. From Fig. 11(c), the miss distances between the attackers and the defender are always larger than R=20 m.However,Attacker 1 and Attacker 2 are in a relatively bad situation and have to perform more maneuver to evade from the defender.After the end of AD engagement at 3.95 s,the time to go for the attackers to intercept the target is less than 0.6 s.Moreover,it should be noted that the attackers are modeled with first-order dynamics with a time constant of 0.1 s. Therefore, the time window for the attackers to switch from the evasion from the defender to the interception of the target is small. In fact,more simulations have been conducted and it is concluded that a smaller time constant and larger initial defender-target range could be beneficial for the performance of the cooperative guidance law.The former factor represents better maneuvering characteristics and the latter implies more interception time against the target after the AD engagement.

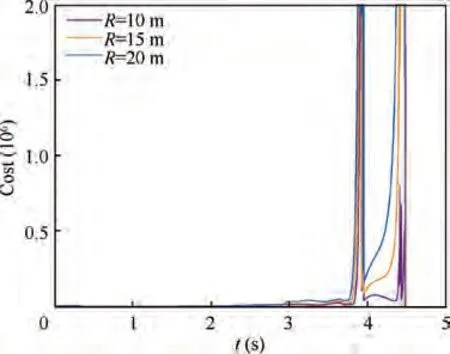
Fig. 12 Scenario 2: Total cost of the attackers in the secondstage optimization

The profiles of the optimized cost in the engagements of scenario 2 are plotted in Fig.12,with the radius of the lethality region chosen as R=10 m, R=15 m and R=20 m, respectively. In scenario 2, the cost of the attackers is rather small with R=10 m comparing with R=15 m and R=20 m.Such range of change to the cost with different R is bigger than that in scenario 1. The cost mainly represents the energy required for the attackers to escape from the defender and intercept the target. The cost profiles have two peaks, one caused by the evasion and the other caused by the interception. Under these circumstances,the attackers have trouble in both evasion and interception. Because of less time to go for the interception, the attackers must perform large maneuver to avoid the miss of the target, which is the origin of the second peak.

6. Conclusions

A guidance engagement between multiple attackers and an active defense target was considered, where the attackers tried to intercept a target from multiple directions. The nonlinear engagement was linearized such that the problem could be solved by linear differential games. Closed-form cooperative guidance laws were obtained in the framework of two-player differential game, where the two opponents are the attackers and the target-defender team. The derivation of the guidance law requires the parameter of the desired miss distances of the attackers-defender engagement; hence a second stage low-computation-effort optimization was performed to obtained the optimal sub-optimal values. The simulation results presented in this paper demonstrate that the multiple attackers are capable of evading from the defender and intercept the target by imposing relative intercept angle. In the attackers-defender engagement, the defender could interfere more than more attacker if it is located in the course between the attackers and the target. The attackers and the defender possessed the same saturation limit and the attackers being intercepted would disengage themselves from the defender when the defender is saturated. It is also shown that a larger lethality region radius of the defender makes the defender more threatening to the attackers and the attackers should paid much more effort to evade from the defender.

This work was supported by the Science and Technology Innovation 2030-Key Project of‘‘New Generation Artificial Intelligence”, China (No.2020AAA0108200), the National Natural Science Foundation of China (Nos. 61873011, 61922008,61973013 and 61803014), the Defense Industrial Technology Development Program, China (No.JCKY2019601C106), the Innovation Zone Project, China (No.18-163-00-TS-001-001-34),the Foundation Strengthening Program Technology Field Fund,China(No.2019-JCJQ-JJ-243),and the Fund from Key Laboratory of Dependable Service Computing in Cyber Physical Society, China (No. CPSDSC202001).