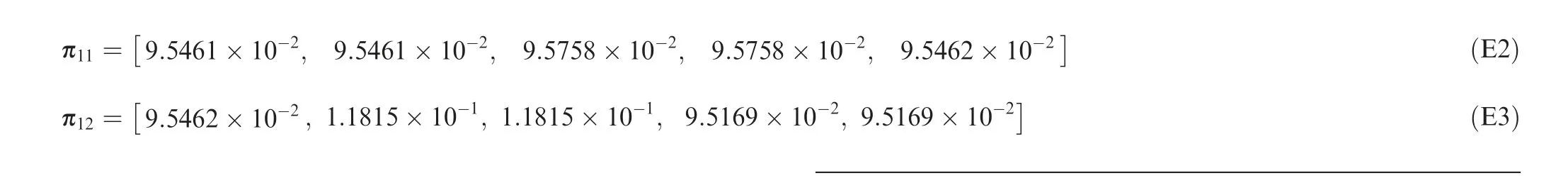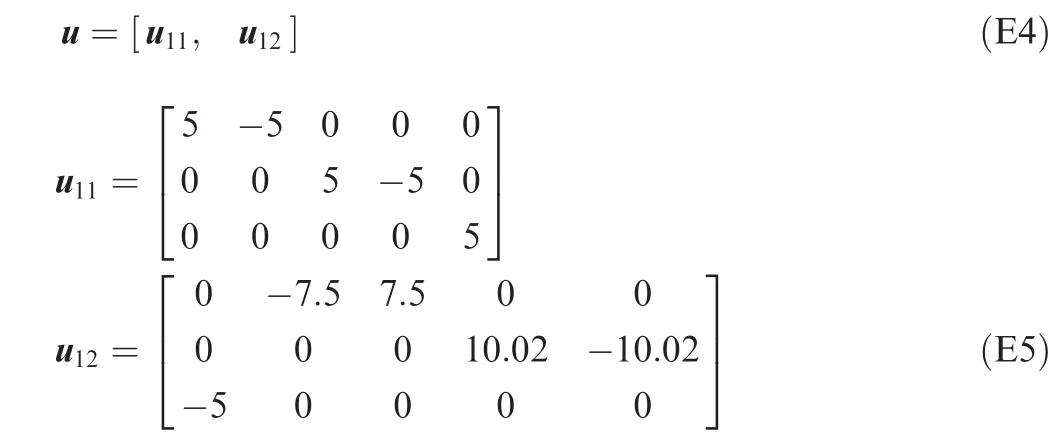Gaussian mixture model based adaptive control for uncertain nonlinear systems with complex state constraints

Yuzhu BAI, Rong CHEN, Yong ZHAO, Yi WANG

a College of Aerospace and Engineering, National University of Defense Technology, Changsha 410073, China

b Nanjing Research Institute of Electronics Technology, Nanjing 210000, China

KEYWORDS Gaussian mixture model;Nonlinear systems;State constrained;Terminal sliding mode control;Uncertain

Abstract This paper addresses an uncertain nonlinear control system problem with complex state constraints and mismatched uncertainties. A novel Gaussian Mixture Model (GMM) based adaptive PID-Nonsingular Terminal Sliding Mode Control (NTSMC) (GMM-adaptive-PID-NTSMC)method is proposed. It is achieved by combining a GMM based adaptive potential function with a novel switching surface of PID-NTSMC. Next, the stability of the closed-loop system is proved.The main contribution of this paper is that the GMM method is applied to obtain the analytic description of the complex bounded state constraints, ensuring that the states’ constraints are not violated with GMM-based adaptive potential function. The developed potential function can consider the influence of uncertainties. More importantly, the GMM-adaptive-PID-NTSMC can be generalized to control a more representative class of uncertain nonlinear systems with constrained states and mismatched uncertainties. In addition, the proposed controller enhances the robustness,and requires less control cost and reduces the steady state error with respect to the Artificial Potential Function based Nonsingular Terminal Sliding Mode Control (APF-NTSMC),GMM-NTSMC and GMM-adaptive-NTSMC. At last, numerical simulation is performed to validate the superior performance of the proposed controller.

1. Introduction

Over the past decades, the control problem of nonlinear systems has attracted considerable interests, and the high performance controller design for nonlinear systems has been widely developed.However,there still exist many long-standing yet unsolved well-documented problems. For example, there has been no unified control framework to deal with uncertainties in nonlinear control systems which significantly deteriorate the control performance.As a result, the uncertain nonlinear systemhas been paid increasing attentions. Specifically, system uncertainties are generally categorized into two main types: the matched uncertainty and the mismatched uncertainty. The matched uncertainty refers to the uncertain terms directly influenced by the control input, i.e., the matched uncertainty and the control effort co-exist in the same dynamics.Hence,this kind of uncertain system can be solved by corresponding control law design. In addition, the control law is easy to design for nonlinear system with the matched uncertainty and has been well researched in recent years.The mismatched uncertainty refers to the uncertain components of systems without any control input.As some states are not directly affected by the control effort,an indirect control input can be generated by the matched part of the system to suppress the influence of the mismatched uncertainty. Therefore, up to now, the practical controller design for the nonlinear systems with the mismatched uncertainty still remains a challenge.

Furthermore, in terms of the controller design problem for the nonlinear system with mismatched uncertainty, several robust control techniques have been proposed, such as PID control,fuzzy control,output feedback control,adaptive control,fault-tolerant control,and Sliding Mode Control (SMC).Meanwhile, these control methods are often combined to achieve better performance. Among them, the SMC has been shown to have stronger robustness compared to others. Owing to this advantage, the SMC has been widely applied to solving mismatched uncertainties of the nonlinear system in recent years. In Ref. 14, a sliding mode surface is developed by the tracking error, and then a fixed-time controller is designed by an adaptive reaching law and a fixedtime mismatched disturbance observer.In Ref.15,an adaptive fuzzy logic based function was proposed to approximate both the matched uncertainty and the mismatched uncertainty, and an iterative multi-surface SMC is designed. With the help of the novel disturbance observers designed to improve the estimation performance,the corresponding observer-based SMC are proposed to deal with the mismatched uncertainty.Furthermore, the nonsingular terminal SMC was presented for uncertain systems.The proposed schemes not only retain the advantages of conventional SMC, including fast response, easy implementation, and robustness to uncertainties,but also make the system states reach the control objective point in finite time. Nevertheless, when applying the integral SMC to accommodate the mismatched uncertainty,the above-mentioned studies do not take the state constraints into account.

As the main factor affecting system performance, state constraints inevitably exist in the actual industrial process,such as robotic manipulator,spacecraft dynamics system,permanent magnet synchronous motor,singlerod electrohydraulic actuator,financial risk management,2solid oxide fuel cells,etc. The main control strategies for preventing the violation of state constraints include model predictive control,the integral constrained optimal control,the prescribed performance control,integral SMC,etc. Specifically, Tarczewskicombined the model predictive control with a linear state feedback controller, and a constrained state feedback speed control is developed for a permanent magnet synchronous motor. To handle the constraints on both the control and the state variables in the financial risk management scenarios, the class constrained linear-quadratic optimal controllers were designed in Ref.26. Based on model predictive control and variablestructure SMC, the integral SMCs are designed for the thermal behavior of solid oxide fuel cells considering state and actuator constraints.However, compared with the state constraints in practical industrial process, the descriptions of them in Refs. 20-31 are simplified.

The previous researches, which dedicate to the controller design of nonlinear system with mismatched uncertainty and state constrains, have some of the following weaknesses:

(1)Almost all the state constraintsare defined by a single predefined inequality system. However, in practical industrial process, the state constraints are so complex that need to be defined with several inequalities. For example, when dealing with the obstacle avoidance problem in the presence of complex shape,it is difficult to describe the state constraints with one single inequality system. The application of the presented controllers in Refs. 20-31 is limited. Furthermore, most of those control approaches do not consider the complex state constraints and the mismatched uncertainty simultaneously, which further deteriorates the system performance and even induces instability.

(2) Most of the existing approaches are applicable only for systemswith particular models and most of them achieve the global stability by governing the closed-loop system.Moreover,it is difficult to reach the low control cost while maintaining the high steady control accuracy in the presence of state constrained and mismatched uncertainty.

Motivated by above discussion, this paper investigates the control problem for nonlinear system with state constraints and mismatched uncertainty. The main contributions can be summarized as follows:

(1) A more representative class of nonlinear systems with mismatched uncertainty and complex state constraints is investigated, and a general control framework is presented, which significantly broaden the application and the field of presented controllers.

(2) A novel GMM-based adaptive potential function is designed to account for the complex state constraints and the uncertainties simultaneously. The main idea of GMM is to approximate an arbitrary probability density function by a finite sum of weighted Gaussian density function, and it has been applied in model construction,uncertainty propagation,fault detection,etc. In this paper, the complex state constraints are analytically described by using the GMM method, which provides the foundation for the novel controller design considering the influence of complex state constraints. Furthermore, to consider the influence of uncertainties, the novel GMM-based adaptive potential function is proposed.

(3) Combing the benefits of the GMM-based adaptive potential function, the PID and the switching surface of the NTSMC, the GMM-adaptive-PID-NTSMC controller is proposed. In comparison with existing controllers in Refs. 7-31,the proposed controller can handle the uncertain nonlinear systems in the presence of mismatched uncertainties and complex state constraints simultaneously. Furthermore, the proposedGMM-adaptive-PID-NTSMCpreservesome properties of the conventional NFTSMC controller,such as strong robustness,no singularity and less chattering.Moreover,the proposed method further improves the robustness of the system, reduces the control cost and the steady-state error compared with the additionally designed APF-NTSMC,GMM-NTSMC and GMM-adaptive-NTSMC.

It should be emphasized that the proposed GMM-adaptive-PID-NTSMC controller is suitable for most nonlinear systems with state constraints and mismatched uncertainties. To guarantee the effectiveness of the controller,a simulation is given in section V.The simulation takes the spacecraft on-orbit service as the background, uses the nonlinear spacecraft dynamics model, considers the target’s complex shape constraints and mismatched uncertainties, and implements the safe proximity maneuver control. The simulation results prove the high performance of the controller.

The structure of this paper is as follows. The problem formulation is devoted in Section 2.The Gaussian Mixture Model is applied to obtain the analytic description of the complex bounded state constraints and the GMM-based adaptive potential function is proposed in Section 3. Next, the GMMbased adaptive PID-NTSMC is designed and the stability of the overall closed-loop systems is proved in Section 4. The results of the numerical simulation and experimental tests are analyzed in Section 5.Finally,the study’s conclusions are presented in Section 6.

2. Problem formulation

where κ is the number of the predefined inequality systems, in other words,κ is the number of the fully confined space of constrained state.ν is the dimension of x,and thereby the number of fully confined space is also ν-dimension. xand h（·） represent the constrained state parameter and constrained state function of the jth dead-zone state in the dth fully confined space, respectively. The xand xare the minimum bound and the maximum bound of the h（·）. In addition,the following conditions should be satisfied and be given as

Remark 4. As the main factors of deteriorating system performance, the state constraints and the uncertainties often appear in the practical industrial process, such as robotic manipulator,flexible crane system,spacecraft dynamics system,nonuniform gantry crane,stirred tank reactor.However, there are few works dealing with the problem of a controller for the nonlinear system with both complicated state constraints, mismatched and matched uncertainties so far. This paper tries to deal with complicated state constraints and mismatched uncertainties in a unified frame works.

The objective of this paper is to design a novel controller to ensure the high control accuracy,the suppression of the uncertainties existing in closed-loop systems and non-violation of state constraints.

Furthermore, the following notations have been employed across the paper for brevity

3. Guassian mixture model based adaptive artificial potential function

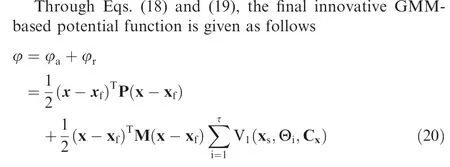
4. Guassian mixture model based adaptive PID-nonsingular terminal sliding mode control

To obtain a more efficient controller, the NTSMC is introduced to combine with GMM-based adaptive potential function and PID controller. The NTSMC provides a variety of design schemes for GMM-based adaptive potential function,considering both state constraints and uncertainties. In this paper, the novel GMM-adaptive-PID-NSTMC is proposed,and the details and sufficient proofs are completed as followings.

4.1. Design of the switching surface

In Ref.33,the Nonsingular Fast Terminal Sliding Mode Control (NFTSMC) is proposed for nonlinear system with time delay. It owns several advantages such as high precision,strong robustness, no singularity, less chattering, and fast finite-time convergence. However, NFTSMC requires too much control cost and is unacceptable in some scenarios.2Therefore, the switching surface of GMM based adaptive NTSMC is designed as follows

Remark 5. Based on Eqs. (21) and (22), the proposed switching surface has the content of GMM, NTSMC and PID. Thus, the proposed switching surface possesses the benefit of the three approaches such as strong robustness,lower state error, no singularity and finite time convergence.These properties are very significant and essential for system Eq. (1). It is because that those properties can compensate uncertainties with the state constraints, eliminate the chattering problem and stabilize the system.

4.2. Design and analysis of GMM-PID-NTSMC

where S（0 ）is the initial value of the GMM-adaptive-PIDNTSMC’s switching surface.

Moreover,based on Eqs.(21) and(A1),the control error e and ˙e will converge to zero within the finite time in the terminal switching surface.

In addition, the APF-NTSMC (Appendix. B), the GMMNTSMC (Appendix. C) and the GMM-adaptive-NTSMC(Appendix. D) is also designed for comparison to depict the superiority of the GMM-PID-NTSMC. Through Eqs. (24)-(29), (B6), (C8) and (D2), the control force of GMMadaptive-PID-NTSMC does not contain any negative fractional power since 1

p/q, and hence it is concluded that from any initial origin states, the closed-loop control system has no singularity.

5. Example

5.1. Example environment

In recent years,on-orbit failures have exceeded launch failures,and cumulatively account for losses of billions of dollars.Among them,many failures are caused by parts and materials failure and most of these failures occur in Telemetry,Tracking and Command(TTC)subsystems.For example,without any assistance from ground personnel, Demonstration of Autonomous Rendezvous Technology (DART)performed a variety of maneuvers in close-proximity to the Multi-Paths-Beyond-Line-of-Sight-Communications (MUBLCOM). However, the GPS receiver of DART suffered from a factory error, causing DART to misjudge its position and velocity continually.Hence, low-velocity collision between DART and MUBLCOM happens. In addition, one of Intelsat New Dawn’s antennas failed to deploy,and hence preventing the utilization of the C-band payload and limiting the operational lifespan of the satellite.Thus,the spacecraft close-range proximity and the space maintenance should be cautious.For these examples,the space maintenance of TTC subsystem is in high demand in space missions that enhances the operational lifetime and capability of space assets.Moreover, the spacecraft close-range proximity with obstacle avoidance in presence of complex shape can be treated as a special situation of system Eq.(1). In particular, due to the existence of sizeable protruding, such as an antenna, the complexity of spacecraft’s shape increases and the difficulty of the collision avoidance problem is enhanced. Thus, the GMM-adaptive-PID-NTSMC is presented to solve the above problems.

Then,the Local-Vertical-Local-Horizontal(LVLH)coordinate frameis utilized to describe the spacecraft relative motion.Furthermore,a state transition matrixfor nonlinear problem of relative motion on an arbitrary elliptical orbit is given as

where r=6.7781336×10m is the semi-major axis of the orbit of the target spacecraft and μ=3.986× 10m/sis the gravitational constant of the Earth. f and e=0.01 represent the true anomaly and the eccentricity of the target spacecraft, respectively. ω and ˙ω represent the angular velocity and angular acceleration of the target spacecraft, which are computed as

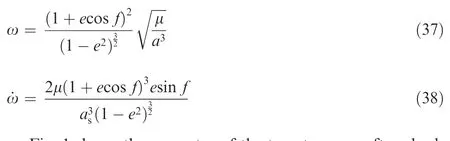
Fig.1 Geometry of the target spacecraft and relative motion of the following spacecraft in LVLH frame.

Fig. 1 shows the geometry of the target spacecraft and relative motion with respect to following spacecraft in LVLH frame. In this numerical simulation, the following spacecraft need to arrive at the desired point, which is near the antenna of the target spacecraft.The movement of the following begins at asterisk 1 and finally arrives at asterisk 2. Furthermore, the physical parameters of the two spacecraft and the initial relative position of the following spacecraft in LVLH frame are given in Tables 1 and 2, respectively.

The period of the control maneuvers and the integration step are both 1 second, and the final time is t=400 s. The GMM is assumed to consist of 10 components. The initial value for K-means is given as

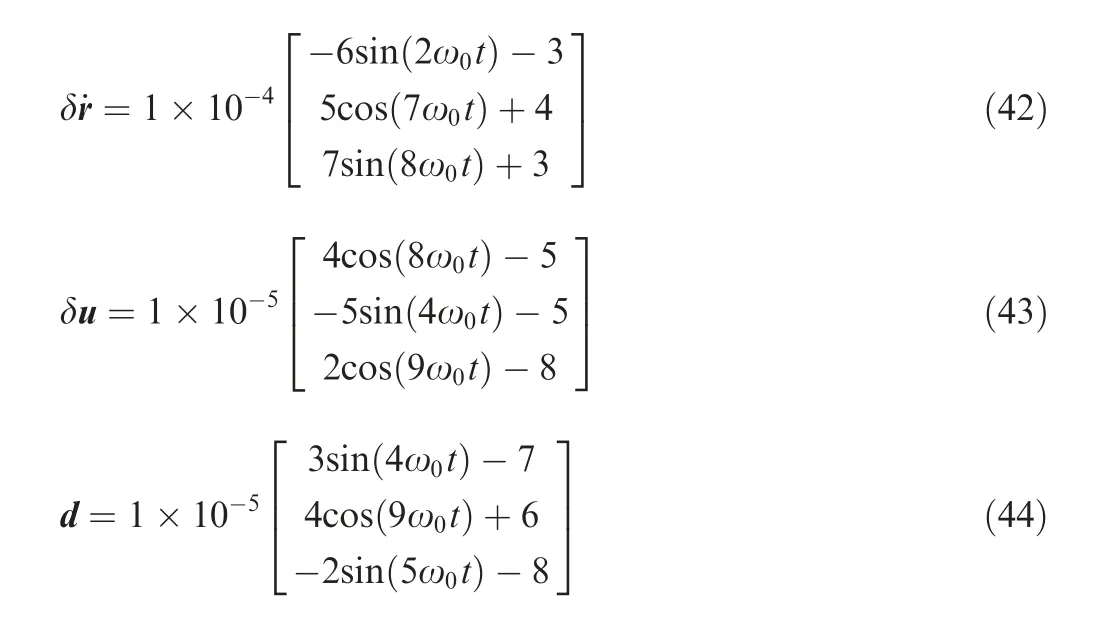
5.2. Results and discussion

Table 1 Physical parameters.

Using the K-means with the initial means in Eq. (39) and EM method, the parameters of the GMM are obtained (Appendix E) and the 3D reconstruction of the target spacecraft with GMM method is shown in Figs. 2. Moreover, Fig. 2(a) and(b) represent the 3D reconstruction of the target spacecraft from different angles.Comparing with Figs.1 and 2,it is noted that the GMM can provide the tractable statistical representation for 3D reconstruction of the complex shape of the target spacecraft.

The proposed GMM-adaptive-PID-NTSMC approach is applied for spacecraft close-range proximity with obstacle avoidance in the presence of a complex shape. In addition,the APF-NTSMC, GMM-NTSMC and GMM-adaptive-NTSMC are utilized for comparison. Fig. 3 shows the change of ln（‖e‖） with APF-NTSMC, GMM-NTSMC, GMMadaptive-NTSMC and GMM-adaptive-PID-NTSMC. Furthermore,Table 3 provides the comparison of control accuracy between APF-NTSMC, GMM-NTSMC, GMM-adaptive-NTSMC and GMM-adaptive-PID-NTSMC. Based on Fig. 3 and Table 3, it is concluded that the control error of APFNTSMC and GMM-NTSMC is much bigger than the GMM-adaptive-NTSMC and GMM-adaptive-PID-NTSMC.Comparing with the GMM-PID-NTSMC’s control error, the control accuracy of GMM-adaptive-PID-NTSMC can reduce to 64.29%.Thus,it is concluded that the GMM-adaptive-PIDNTSMC outperforms other methods.

Fig. 4 shows the actual trajectory of the following spacecraft with GMM-adaptive-NTSMC and GMM-adaptive-PID-NTSMC. From Fig. 4, the GMM-adaptive-NTSMC and GMM-adaptive-PID-NTSMC successfully avoid collision in the presence of the antenna, in other words, the GMMadaptive-PID-NTSMC can guarantee that the state constraints are not violated. This is attributed to the fact that the GMM-based adaptive potential function includes parameters of the complex shape obtained by the GMM method.Although the performance improvement of GMM-adaptive-PID-NTSMC cannot been fully shown in the Fig. 4, it will be analyzed in Table 4 with respect to the velocity change.

Table 2 Initial relative position of the following spacecraft in LVLH frame.

Fig.2 3D reconstruction of the chief with two solar panels and two antennas.

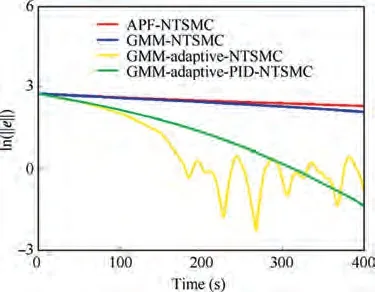
Fig.3 The change of ln（‖e‖） with four control methods.

Table 3 Comparisons of control accuracy.

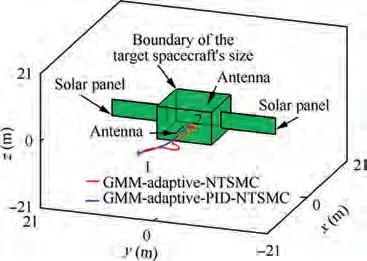
Fig.4 The actual trajectory of the following spacecraft with GMM-adaptive-NTSMC and AGMM-adaptive-PID-NTSMC.

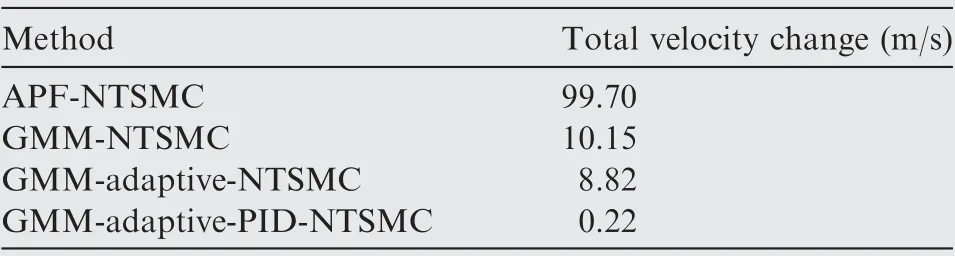
Table 4 Comparisons of total velocity change with four control methods.

Next, the fuel cost is utilized to assess the efficiency of the proposed control laws. It is generally known that the lifespan of the spacecraft depends on the residual fuel. In this paper,the following mathematical model is applied to compute the total velocity change as fuel consumption.

Table 4 shows the comparison of the total velocity change over 400 s for the APF-NTSMC,GMM-NTSMC and GMMadaptive-NTSMC avoidance strategies. As shown in Fig. 4 and Table 4, although the APF-NTSMC has low control expense and can achieve close-range proximity in presence of the antenna, it has the highest total velocity change. Comparing with GMM-NTSMC, the GMM-based control not only guarantees the safety performance of this space mission, but also has lower total velocity change. This is because that the GMM-based potential function considers the influence of the target spacecraft’s complex shape, and hence the GMMNTSMC, GMM-adaptive-NTSMC and GMM-adaptive-PID-NTSMC methods can avoid collision with the antenna and require less total velocity change. Moreover, compared with APF-NTSMC, the GMM-NTSMC can reduce 89.82%of the total velocity change, and the GMM-adaptive-NTSMC and the GMM-adaptive-PID-NTSMC reduce 91.15% and 99.78%, respectively. Note that the GMMadaptive-NTSMC and the GMM-adaptive-PID-NTSMC have the same control algorithm structure, however, the switching surface of the GMM-adaptive-PID-NTSMC is developed by combining the switching surface of the GMM-adaptive-NTSMC and the PID method. As a result, the GMMadaptive-PID-NTSMC can require less control cost and reduce 97.51% of the total velocity change with respect to GMM-PID-NTSMC. In addition, as aforementioned in Section 4, the GMM-adaptive-PID-NTSMC can avoid a singularity problem while the APF-NTSMC, GMM-NTSMC and GMM-adaptive-NTSMC cannot. Thus, the GMMadaptive-PID-NTSMC would be a good candidate to design a controller for the uncertain nonlinear systems with complex state constraints.

6. Conclusions

This paper proposes an GMM-adaptive-PID-NTSMC for a class of uncertain nonlinear system problem with complex state constraints and mismatched uncertainties. The GMMbased potential function, PID control and a novel switching surface of NTSMC are integrated in this work.The main contribution of this paper is that the GMM method is applied to obtain the analytic description of the complex bounded state constraints, and thereby guarantees the non-violation state constraints. Most importantly, the GMM-adaptive-PIDNTSMC can control a more representative class of uncertain nonlinear systems with state constrained and mismatched uncertainty. In addition, the proposed controller enhances the robustness with less control cost and reduces the steady state error with respect to the APF-NTSMC, GMM -NTSMC, the GMM-adaptive-NTSMC. Subsequently, the proposed controller is then applied for spacecraft close-range proximity with obstacle avoidance in the presence of complex shape and uncertainties.Numerical simulation is performed to validate the superior performance of the proposed controller.The proposed method takes complex factors into account and has strong universality. However, in some simple cases,the computational complexity may be a little larger than some existing methods. At the same time, there is still some further improvement of control performance. In the future work, the neural network approximations can be applied to approximate those upper bounds as the adaptive gains to the controller,hence can further reduce the convergence error and the velocity change.In addition,the performance of the developed controller should be verified in practical experiment.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was supported by the National Natural Science Foundation of China (Nos. 61690210, 61690213, 12002383).

Appendix A. Based on the definition of the final GMM-based potential function φ, the gradient ∇φ can be deduced from Eq. (20) with respect to the state vector×of the nonlinear systems Eq. (1), which is given as

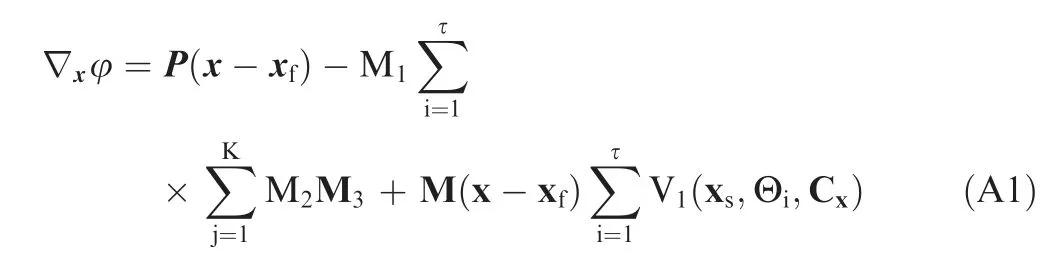
where the parameters ψand σdetermine the height and width of the repulsive potential. The matrix Nis a positive definite matrix and determines the oblateness and orientation of the Gaussian function.The magnitude of the matrix Ndetermines how sharply the repulsive potential decays with distance from the obstacle center.