Detailed modeling of aluminum particle combustion- From single particles to cloud combustion in Bunsen flames
Jirui ZHANG, Oliver T. STEIN, Tien D. LUU, Ali SHAMOONI,Zhixun XIA, Zhening LUO, Likun MA,*, Yuncho FENG,Andres KRONENBURG
a College of Aerospace Science and Engineering, National University of Defense Technology, Changsha 410073, China
b Institut fu¨r Technische Verbrennung, Universita¨t Stuttgart, Stuttgart 70174, Germany
KEYWORDS Aluminum particle combustion;Bunsen flame;Burning time;Burning rate;Particle cloud
Abstract A numerical model for aluminum cloud combustion which includes the effects of interphase heat transfer, phase change, heterogeneous surface reactions, homogeneous combustion,oxide cap growth and radiation within the Euler-Lagrange framework is proposed. The model is validated in single particle configurations with varying particle diameters. The combustion process of a single aluminum particle is analyzed in detail and the particle consumption rates as well as the heat release rates due to the various physical/chemical sub-models are presented. The combustion time of single aluminum particles predicted by the model are in very good agreement with empirical correlations for particles with diameters larger than 10 μm. The prediction error for smaller particles is noticeably reduced when using a heat transfer model that is capable of capturing the transition regime between continuum mechanics and molecular dynamics. The predictive capabilities of the proposed model framework are further evaluated by simulating the aluminum/air Bunsen flames of McGill University for the first time. Results show that the predicted temperature distribution of the flame is consistent with the experimental data and the double-front structure of the Bunsen flame is reproduced well.The burning rates of aluminum in both single particle and particle cloud configurations are calculated and compared with empirical correlations. Results show that the burning rates obtained from the present model are more reasonable, while the correlations,when embedded in the Euler-Lagrange context,tend to underestimate the burning rate in the combustion stage, particularly for the considered fuel-rich flames.
1. Introduction
Aluminum is widely used as an additive in solid rocket propellantsand pyrotechnicsowing to its outstanding characteristics such as high energy density and combustion temperature,environmentally benign products, and good stability. In the past few decades,significant progress has been made in studies of ignition and combustion of single isolated aluminum particles,and Dmodels with very low computational cost have been established for nano-and micron-sizedparticles,respectively.Since the typical mass fraction of aluminum particles in high-energy materials is less than 20%,the interactions among different metal particles can typically be neglected.In this case,correlation models for particle ignitionand combustionbased on experimental data of single aluminum particles are applicable to the simulation of solid propellant combustion.
In recent years, a process referred to as metal fuel cyclehas been proposed, in which metal fuel represented by aluminumacts as a clean and renewable energy carrier to mitigate climate change. One of the related energy conversion methods is to burn the metal fuel directly with air in a combustor to provide clean high-grade heat.In the scenario of metal-fuelled burner, the aluminum particles provide the primary fuel, the concentration of which can be as high as 600 g/m, resulting in an average inter-particle spacing of about 13 particle diameters; therefore, thermal feedback between particles cannot be neglected in particle cloud combustion.Moreover, experiments suggest that rich metal-fuel suspensions are usually required to achieve stable combustion,and under this circumstance, the conversion process of most particles is supposed to occur in the near-zero-oxygen region.Therefore, the diffusion of the evaporated gaseous aluminum and subsequent gas-phase homogeneous reaction should be considered along with the heterogeneous reaction.
In the field of metal particle suspension combustion,recent experimental investigations have shed some light on the combustion characteristics and global flame properties,but detailed information on flame structure,mass and heat transfer processes is difficult to infer from experiments. However,such information can be obtained from numerical simulations of metal particle cloud combustion. Huang et al.performed a detailed analysis which evaluated the effect of particle size at the nano and micron scale on aluminum dust flames. Later,a one-dimensional steady-state model was proposed by Khalili et al., in which the effects of thermophoresis and Brownian motion were included. Recently, Han and Sungproposed a detailed numerical model including radiation and particle surface reactions, and the propagation process of aluminum dust flames under various conditions in a half-open channel was studied.Then,Zou et al.extended the model in Ref.to capture the combustion properties of aluminum nanoparticle clouds.They approximated the flame speed by the propagation speed of the ignition front,with the latter being defined by the minimum gas temperature that can ignite a single aluminum particle.
An inherent limitation of many previous numerical studies is the direct application of experimental correlations derived from single particle combustion measurements in particle cloud models. For instance, particle burning time obtained from experimental data has been used in previous studies to determine the burning rate of the particles.In this case,macro parameters required for the correlations, such as the gas temperature and oxygen concentration, that refer to the far-field conditions of the combustion chamber in the original experiments are approximated by the state of the gas that immediately surrounds the target particle.The suchobtained governing scalars are then used to calculate the consumption rate of the particles at every time step, which may lead to significant errors.
To overcome these limitations, the objective of the present study is to establish a detailed numerical model for aluminum particle cloud combustion in the Euler-Lagrange framework,which is based on fundamental physics and avoids the use of very general empirical correlations for key quantities, such as ignition temperature and burning time. The model considers the effects of interphase heat transfer,phase change,heterogeneous surface reactions and homogeneous chemistry,as well as oxide cap growth.By simultaneously integrating these physicochemical sub-models, their interaction is directly computed,for example the competing effect of evaporation and heterogeneous surface reactions for particle consumption, among others. Another contribution of this work is that the radiative heat transfer is modeled by solving the full 3D radiative transfer equation,and the effects of dispersed particles on radiation emission, absorption and scattering are all included. The new model is then used to study single particle combustion and Bunsen flames of aluminum particles in detail, and the experimental aluminum Bunsen flame is reproduced numerically for the very first time,which acts as a solid validation case for the present model.
2. Modeling
2.1. Modeling of dispersed phase
The dispersed phase particles under consideration feature a spherical core of solid aluminum (Al) surrounded by a thin surface layer of aluminum oxide(alumina,AlO).The Al core has an effective diameter d,while the total particle diameter comprised of Al and AlOis denoted as d. It is noted that there are two formation routes of the final product of the oxidation process,AlO,in the present study.The first is Heterogeneous Surface Reaction (HSR), which leads to the newly formed AlOdirectly condensing on the particle surface and remaining a part of the Lagrangian dispersed phase. The second type of AlOis the final product of homogeneous Al oxidation,which exists as a finely dispersed smoke and attributes to the continuous Eulerian phase. Moreover, it is common practice to assume that Al particles with diameters larger than 20 μm burn in the diffusion-controlled regime,while for nanosized Al particles heterogeneous surface reactions become more important, which indicates kinetically-controlled combustion.The diameter of the Al particles used in the target Bunsen flame is about 5.6 μm, and their combustion mode should therefore be under the joint control of diffusion and chemical kinetics.Hence,both heterogeneous surface reactions and homogeneous gas reactions, as well as diffusion processes in the gas phase are considered in the combustion process of the Al particles in the present study.
The dispersed particles are described in the Lagrangian framework and their interaction with the gas phase is characterized by the transfer of mass,momentum and energy.Moreover,particle collisions are neglected in the present study.This assumption is reasonable because the dust concentration of the Al dust flame under consideration is about 500 g/m, corresponding to an average particle spacing of about 14 particle diameters.
The evolution of the particle temperature, T, is written as

where μ is dynamic gas viscosity.
The change of the particle mass is due to evaporation and HSR, and can therefore be expressed as
2.2. Aluminum combustion sub-models
The models to describe the principal physical and chemical processes occurring in aluminum particle combustion are provided in the present section,considering interphase heat transfer, melting, evaporation, surface reaction, and radiation.

where Pris the particle Prandtl number.
When particle sizes are of the order of microns, the treatment of the surrounding gas as a continuum may become questionable.Following Ref.26, particles with a diameter of 5.6 μm, which is the size of the aluminum particles employed in the Bunsen flame experimentstargeted here, are subject to the transition regime for heat transfer.Therefore,the Kavanau correlationfor the Nusselt number in the transition regime is employed in the present study

where his the heat release from the surface reaction,which is calculated as

2.2.5. Radiation model
Compared with the simplified 1D radiation models used in previous studies,radiation is modeled by solving the full 3D Radiative Transfer Equation (RTE)in the present study under the assumption of grey particles and grey gas with negligible scattering. The condensed phase alumina is assumed to exist as a very fine smoke,which we model as a continuous Eulerian species with an emissivity much higher than the remaining gas phase. Therefore, the gas absorption/emission coefficient, κ, is calculated as


2.2.6. Oxide cap growth model
When the particle temperature exceeds the melting point of alumina,the oxide layer slides on the surface of the liquid aluminum core to form an oxide cap due to surface tension.In the present study,oxide cap growth model proposed in Refs.38,39 is employed to consider the effect of the oxide cap on the reactive surface of the Al particle.Based on the geometric relationship shown in Fig. 1,the following equations can be obtained:

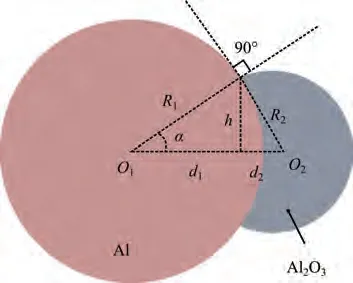
Fig. 1 Geometry of aluminum droplet with oxide cap.39

2.3. Modeling of carrier gas phase
2.3.1. Governing equations of gas phase

Considering the assumption of a unity Lewis number, the energy equation can be written as

2.3.2. Homogeneous chemistry
Table 1 shows the homogeneous chemistry adopted for the present study.It is composed of 8 species and 11 chemical reactions.Since AlOdoes not prevail as a stable gas phase species,an irreversible reaction is used to describe the transition from gaseous to condensed phase AlO, denoted as AlO(l) in Table 1. As stated above, the condensed alumina from the homogeneous reaction is assumed to exist as a very fine smoke and attributed to the Eulerian gas phase, which is a common practice in aluminum particle combustion.
3. Numerical details
3.1. Computational configurations
3.1.1. Single aluminum particle
To evaluate the behavior of the various aluminum sub-models as well as their interaction in the overall combustion model,we consider the combustion of a single particle in a hot coflow environment. The computational domain features a cuboid and it spans L=105d,L=L=65d. As shown in Fig. 2,a single aluminum particle is fixed in the flow field at(27.5d,32.5d,32.5d). According to Ref.40, the thickness of the initial oxide layer (AlO) of the particle with diameters varying from 0.01 μm to 25 μm is generally between 2 nmand 4 nm; therefore, it is assumed that the thickness of the oxide layer of all particles is 4 nm in the present study. The domain is discretized into 21×13×13 cells, which results in a mesh resolution of 5d. The initial gas temperature in the domain is set to 2500 K. Preheated air flows in from the left boundary with a fixed velocity(U) of 0.4 m/s and a temperature(T) of 2500 K. Zero-gradient outflow conditions are used for all other boundaries.
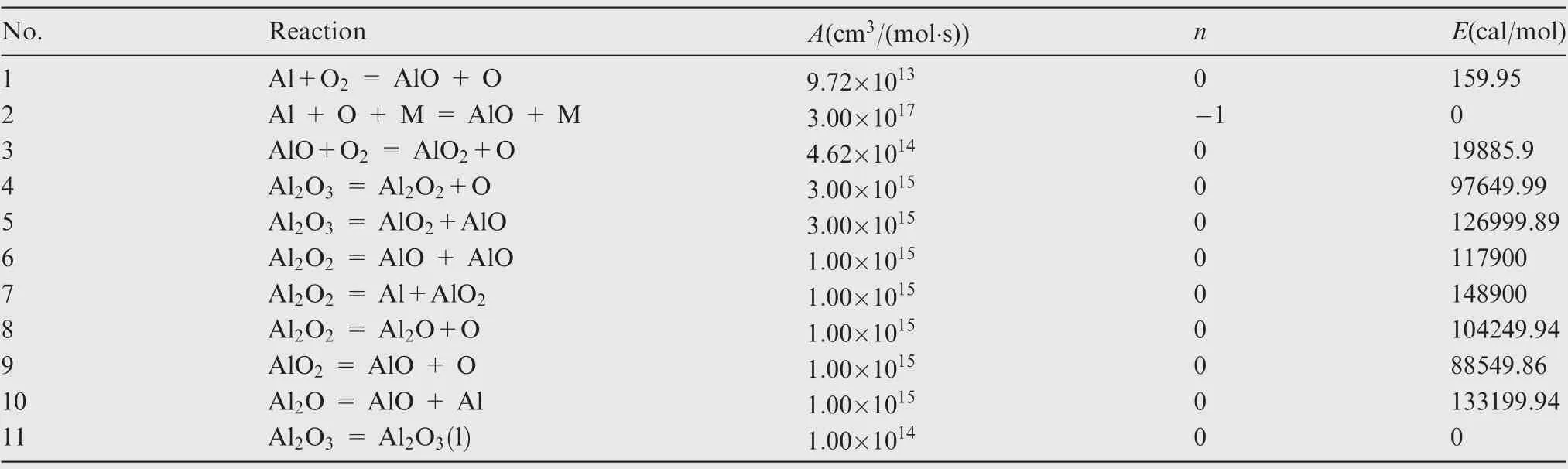
Table 1 Al/O mechanisms, k=A×Tn exp (-E/RT).
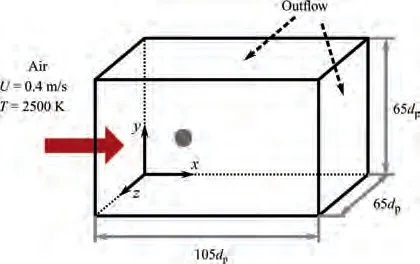
Fig. 2 Computational domain and boundary conditions for single aluminum particle combustion.
3.1.2. Aluminum Bunsen flame
The second configuration considered in this study is Al cloud combustion established on the Bunsen burner of Goroshin et al.27, in which an aluminum/air flame was stabilized above a nozzle with an exit diameter of 20 mm. To limit the computational cost of the simulations,an axi-symmetric geometry,as demonstrated in Fig. 3, is used in the present study.The computational domain is a wedge with an angle of 3°to represent a cylinder with a total radius of 40 mm and a length of 80 mm.The domain is discretized into 200 grid points in the radial direction and 400 grid points in the axial direction, resulting in a mesh resolution of 200 μm. As shown in Fig. 3, the aluminum particles are carried by air and have the same inlet velocity(U)of 0.5 m/s and temperature of 300 K as the carrier gas(red area).The coflow of air(blue area)is assumed to have the same velocity as the central jet.The width of the nozzle wall is 1 mm in the present configuration.The dust concentration at the nozzle outlet is 500 g/m, which is the same as the experimental operating condition.Moreover, all reported quantities of the Al Bunsen flame are averaged within 0.1 s after flame stabilization.
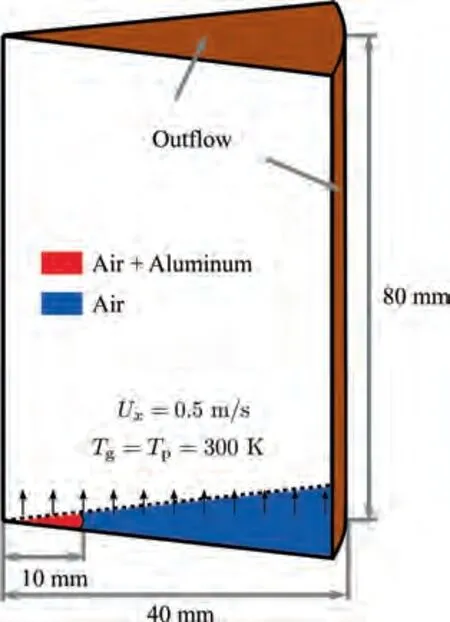
Fig. 3 Computational domain and boundary conditions for aluminum particle Bunsen flame.
3.2. Numerical setup
All simulations reported in this study are carried out using the open-source CFD package OpenFOAMv1912.The underlying reacting two-phase solver is based on our previous work documented in Ref.43 and has been extended to consider the detailed Al modeling framework described in Section 2 for the present contribution. There are nearly 130000 particles in the computational domain of the Al Bunsen flames, resulting in an average number of about 5 particles per cell. The simulation cost of the Al Bunsen flame is approximately 5000 CPU hours, in which the time step is set to 5×10s.
The transport equations are spatially discretized with a finite volume method.The convection terms in the momentum equation are discretized with a second-order linear upwind differencing scheme, while those in the scalar equations are discretized with a second-order limited linear differencing scheme.The diffusive terms are discretized with an unbounded second-order central differencing scheme. For time integration, the second-order implicit backward scheme is used.
4. Results and discussion
4.1. Single particle combustion
4.1.1. Combustion process analysis

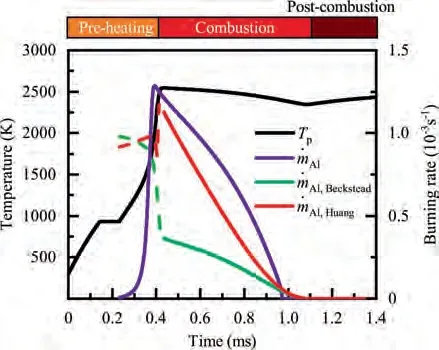
As demonstrated in Fig.4 (a),the particle is initially heated up to the melting point of Al, 933 K, and its temperature remains constant until melting is complete, that is,Y=0,indicated in Fig.4 (b).Similarly,when the particle temperature reaches the melting point of alumina around 0.4 ms, as shown in the inset of Fig. 4 (a), melting of alumina proceeds at a constant temperature of 2327 K,followed by further heat-up of the particle. Fig. 4 (c) reveals that the main heat source for heating and melting the particle mainly comes from the interphase heat transfer between the two phases, but this contribution becomes continuously weaker as the particle temperature rises. The density of Al decreases with increasing temperature, and mass loss due to evaporation is small in the early stage of preheating; therefore, the particle size increases continuously for 0.14 ms
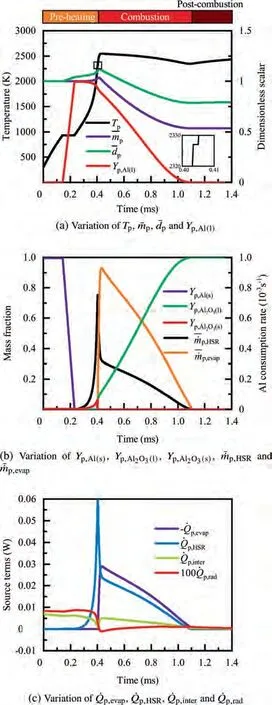
Fig.4 Combustion process of a single particle with dp =10 μm.
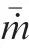
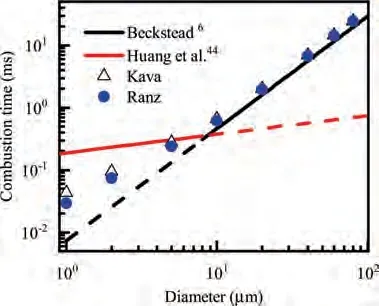
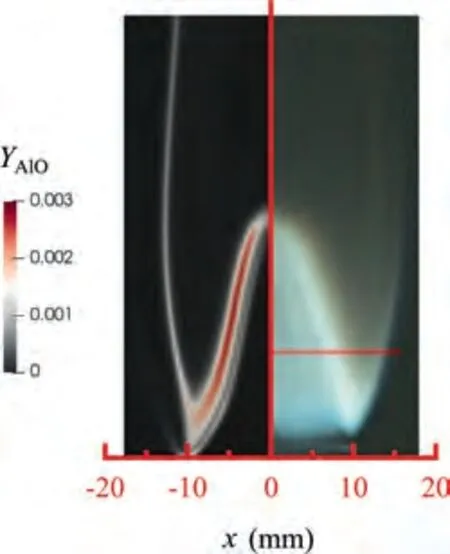
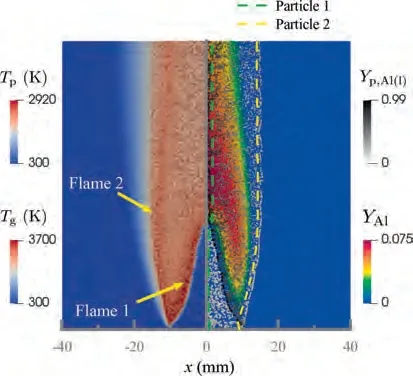
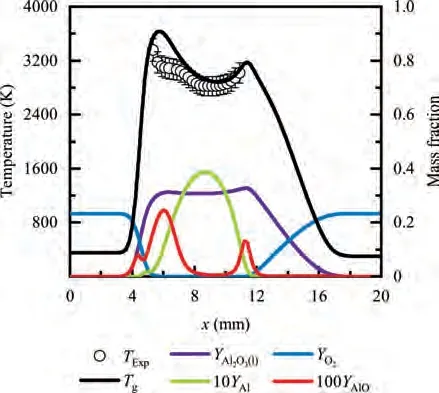
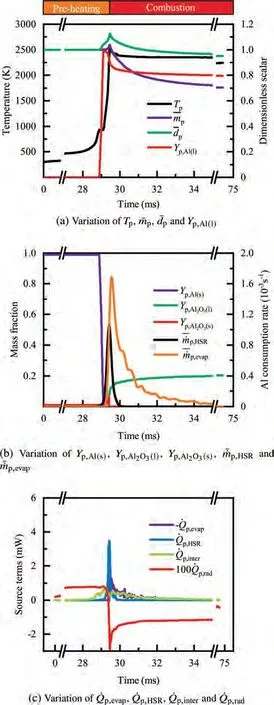
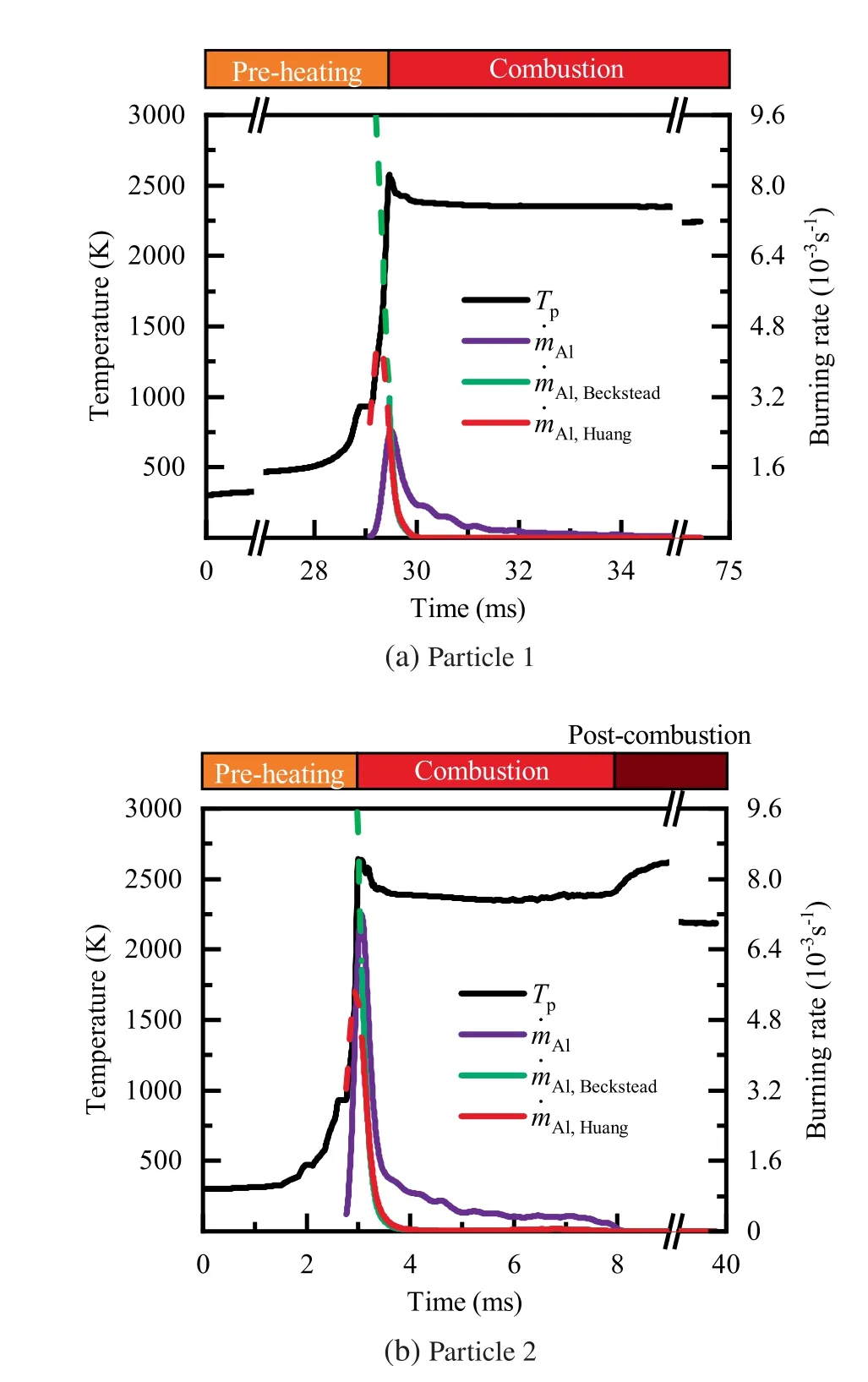
During the combustion stage,for 0.43 ms The end of the combustion stage is marked at t=1.1 ms in Fig.4,in which Y=0.In the final post-combustion stage,all Al in the particle has been consumed and turned into liquid AlO(Fig. 4 (b)), and the particle temperature starts to rise under the heating of the hot gas environment. Fig. 5 compares the simulation results for the combustion of a single aluminum particle with a diameter of 10 μm using different interphase heat transfer models. Subscripts ‘‘Ranz”and ‘‘Kava” indicate the Ranz-Marshall(Eq. (7)), and Kavanau(Eq. (8)), correlations, respectively. The results demonstrate that, for the studied conditions, the Ranz-Marshall model predicts a stronger heat exchange rate between the particle and surrounding gas, i.e., the Nusselt number of the particle, which leads to an earlier ignition. After the particle is ignited, the combustion process is weekly dependent on the gas temperature,and the heat required for aluminum particle evaporation mainly comes from HSR. Since a unity Lewis number is employed in the present study, the Ranz-Marshall model also predicts a higher Sherwood number, resulting in a higher evaporation rate during combustion (not shown).This is the reason for the somewhat lower particle mass in the post-combustion stage when the Ranz-Marshall model is used. Fig. 5 Effect of interphase heat transfer model on particle combustion process with dp =10 μm. To evaluate the effect of the particle diameter on combustion time, eight cases of single aluminum particle combustion with different diameters,varying from 1 μm to 80 μm,are simulated. Fig. 6 presents the combustion time obtained in the present study, compared with the burning time correlations in Refs.. It should be noted that these two correlations have been derived for aluminum particles of different sizes,i.e., the first one for particles with diameters greater than 10 μm,and the second one for nano- as well as sub-micronsized particles.The results in Fig. 6 indicate that the present model can accurately predict the burning time for Al particles with diameters greater than 10 μm. Moreover, the difference between the combustion time calculated using the Kavanau and Ranz-Marshall models for interphase heat transfer is negligible for particles with diameters larger than 10 μm. However, the difference between the model predictions can be as high as 39.1%for a particle with diameter of 1 μm,which indicates that the transition regime heat transfer should be considered for Al particles with diameters smaller than 10 μm. It can be seen from Fig.6 that although the prediction error of the combustion time calculated using the Kavanau model is greatly reduced compared with the results from the uncorrected interphase heat transfer model, there is still a noticeable gap between the present study and the correlation in Ref.44. One possible reason for these deviations may be that the influence of the unresolved gas near the particle surface, which is the inherent limitation of the Euler-Lagrange framework,becomes more significant as the particle diameter decreases. Moreover,the present one-step HSR model may not be refined enough,compared with the complex polymorphic phase transformation processesand chemistry reactionsreported in the literature.These two issues will be addressed in future work. 4.1.2. Combustion rate analysis Fig. 6 Combustion time calculated in present simulations with different interphase heat transfer models, compared with the correlations by Beckstead6 and Huang et al.44 . The in-depth analysis of Al particle burning shown in the previous Section 4.1.1 has demonstrated that the combustion of single Al particles is a complex process controlled by both heat and mass transfer, and it is doubtful that simply using empirical correlations can accurately describe the entire combustion process.Therefore,a comparative investigation of the burning rates calculated by the present model and burning time correlations from previous studies is carried out. The burning rate of the aluminum particle in the present model is calculated as where dis in cm, tis in s, E=73.7 kJ/mol. A priori analysis is carried out to directly compare the results from the empirical correlations to the burning rate obtained from the present model. Hence, instead of simulating another two cases with the correlation-based combustion models, the parameters in Eqs. (44)-(45) are dynamically evaluated during the simulation using the present model. Such comparison is able to show the difference in the burning rates obtained from different models under the exact same condition at each time step. Hence, Tand Xare approximated by the gas temperature and oxygen concentration of the Eulerian cell in which the particle resides and,along with the particle diameter,these quantities are updated at every time step. Fig. 7 compares the burning rates calculated by the different methods,and the results indicate that different models will lead to completely different combustion rates.The dashed line indicates the correlation-based combustion rates in the preheating stage,and solid lines show the correlation-based combustion rates in the combustion stage. All burning rates are normalized by the initial particle mass. As can be seen in Fig. 7, the correlation-based methods tend to underestimate the burning rate during the entire combustion stage,compared with the present simulation. The main reason for this bias of the burning rate is the different method of evaluating the governing variables that affect the rate. Specifically, the parameters in the empirical formulae for the combustion time, Eqs.(44)-(45),are supposed to reflect the macroscopic parameters of the entire oxidation environment where the aluminum particles are burned (‘‘far-field” conditions). However, as already stated above, in the present Euler-Lagrange simulations, the governing parameters describing the oxidation environment surrounding the particle are the spatially-averaged scalars over the Eulerian cell in which the particle is located. Although the cell volume is much larger than the particle size, the oxygen concentration and all other scalars are locally affected by the particle conversion process. Therefore, in the combustion stage, a large amount of aluminum vapor is evaporated from the particle, which acts to reduce the oxygen concentration in the local cell. Moreover, a flame located near the particle will consume oxygen and reduce its availability for HSR even further. As a result, the local cell values considered for the burning time correlations in the Euler-Lagrange approach tend to have a higher temperature and lower oxygen concentration compared with far-field conditions. Considering Eqs.(43)-(45), the following estimation can be made: Comparing conventional far-field conditions (T= 2500 K, X=0.21) with typical near-field values during particle combustion(T= 3000 K, X= 0.1), the particle burning rate for a 10 μm particle is 50.61%or 14.01%lower when using the local cell values in Eq. (44) or Eq. (45), respectively. Hence the underestimation of the burning rates shown in Fig. 7 seems reasonable. Fig. 7 Temporal variation of particle burning rate during the combustion process of a single aluminum particle with dp =10 μm. As a more stringent test of our newly developed Euler-Lagrange framework for Al combustion, we simulate particle cloud combustion stabilized on the laminar Bunsen burner from McGill University.Fig. 8 first compares the predicted AlO distribution with a photograph of the experimental flame.Yis the average mass fraction of AlO. The horizontal red line shown on the right of Fig. 8 is the sampling line for measurements in the experiment at a height of 12 mm above the burner. It is also used for data extraction in the present simulation. AlO is selected for this comparison because it is a critical intermediate of aluminum/air combustion and high levels of AlO are characteristic for regions with strong homogeneous chemical activity.Moreover, its spectral emissivity is relatively strong, and it is usually used as a characteristic signal of aluminum gas phase combustion.As can be seen in Fig.8,the predicted flame structure is generally consistent with the experimental observation, and the experimental doublefront structure with an inner (conical) and outer (jet-type)flame is reproduced successfully. Fig.8 Structure of aluminum Bunsen flame (left: predicted AlO distribution;right:photograph of aluminum Bunsen flame in Ref.27). Fig.9 Contour of average gas temperature Tg (left)and average mass fraction of aluminum YAl (right). Fig. 9 illustrates the structure of the Al Bunsen flame.Fig.9 (left)presents a snapshot of the average gas temperature and the particles are colored by their instantaneous temperature. Fig. 9 (right) shows the average distribution of gaseous Al and the particles are colored by their liquid Al mass fraction. Similar to the AlO distribution shown in Fig. 8, the gas temperature profile also presents a double-front structure,with an inner Flame 1 and outer Flame 2.This is because the target Bunsen flame is a fuel-rich flame with a dust concentration of 500 g/m, and major amounts of gaseous Al evaporated from the dispersed phase can be observed in the middle of the domain downstream of Flame 1.Moreover,an outer diffusion flame fed by the mixing of vaporized Al from the center and oxygen from the co-flow is formed and referred to as Flame 2. Focusing on the dispersed phase, particles that are injected near the edge of the nozzle at around x=10mm (outer particles, yellow trajectory) enter the flame front in a relatively short time and are ignited earlier.In contrast,particles injected via the central part of the nozzle (inner particles, green trajectory) undergo a longer preheating stage. In the downstream region of the flame, outer particles have a higher burning rate than the inner particles, and there is still residual liquid Al remaining in many inner particles near the outlet of the domain, indicating that these particles are not fully burnt. A more detailed analysis of the evolution of such inner and outer particles is presented below. Fig. 10 compares the gas phase temperature predicted by the present simulation and the measured condensed phase temperature distribution at a height of 12 mm above the burner for the target Bunsen flame. Trefers to the temperature measurement in Ref.27, and Tis the mean gas temperature predicted by simulation. Y,Yand Yare the predicted mean mass fractions of gaseous aluminum, oxygen, and condensed alumina, respectively. The temperature of the condensed phase was obtained by fitting the continuum spectra of the dust flame in the 400-900 nm spectral range to Planck’s law, and the measurement error is about 5%, as reported in Ref.27, which has been used to determine the width of the error bar in Fig. 10. The condensed phase temperature measured in the experiment has been used for our comparison.This is because it is the only quantitative data in Ref.27, the spatial distribution of which has been recovered from the raw measurement data by means of Abel deconvolution.Moreover, the condensed alumina is modeled as a continuous Eulerian phase in the present study,so that the condensed and gas phase are at thermal equilibrium. The results indicate that the predicted temperature agrees well with the measurements and the radial profile of temperature is also well reproduced.The ‘‘M” shape of the temperature distribution is attributed to the existence of the secondary outer diffusion flame, which has been explained in the previous discussion on Fig. 9. As shown in Fig. 10, the oxygen mass fraction remains constant in the inner part of the flame, for 0 mm Fig. 10 Temperature and species mass fraction distribution at a height of 12 mm above burner of Bunsen flame from Ref. 27. Fig.11 Combustion process of‘‘Particle 1”in Bunsen flame,the trajectory of which is shown in Fig. 9 by green dashed line. In order to get a better understanding of the particle characteristics inside the Al dust flame, two typical particles, the trajectories of which are illustrated in Fig. 9, are extracted from the particle cloud and their properties versus time are shown in Fig. 11 and Fig. 12 repectively. The time on the abscissas corresponds to residence time of the particles inside the computational domain. Fig.12 Combustion process of‘‘Particle 2”in Bunsen flame,the trajectory of which is shown in Fig. 9 by yellow dashed line. As can be seen in Fig. 11, Particle 1, injected in the central region of the nozzle, does not fully convert inside the domain.This can be inferred from the fact that there is still a significant amount of liquid aluminum remaining in the particle at 73 ms,which corresponds to the time shortly before the particle leaves via the domain exit.Due to a lack of oxygen in the central part of the fuel-rich Bunsen flame, as already discussed in the context of Fig. 9, the reaction rate of HSR decreases to zero quickly(Fig. 11 (b)). Fig. 12 illustrates the evolution of the outer ‘‘Particle 2”, injected at the edge of the Bunsen flame,the preheating stage of which is much shorter compared with Particle 1 injected at the center, and three sub-stages can be clearly identified, as shown in Fig. 12 (a). Because of a lack of oxygen in this Bunsen flame, HSR only occurs during the beginning of the combustion stage of these two particles, as demonstrated in Fig. 11 (b) and Fig. 12 (b). Therefore, the interphase heat transfer becomes the main contributor to the heat required for evaporation in the combustion stage, as shown in the inset of Fig.12 (c),in which the curves representing these two source terms almost coincide. Fig. 13 Temporal variation of particle burning rates during combustion process of two typical aluminum particles in Bunsen flame. The burning rates of the two aluminum particles that were tracked along the dust flame are shown in Fig. 13, and compared with the correlation-based models from Refs6,9.Similar to the case of the single particle that is shown in Fig. 7, the correlation-based methods underestimate the burning rate of the aluminum particles in the Bunsen cloud as well, and this bias of the prediction of the burning rate is increased compared with the single particle combustion case.The target Bunsen flame is fuel-rich; therefore, the oxygen concentration is almost zero in the region between the two reaction zones, as demonstrated in Fig. 10. Hence, the instantaneous burning time of the particles passing through this zone predicted by Eq. (44) or Eq. (45) can be very large, resulting in extremely small burning rates in the combustion stage. On the other hand, the burning rate calculated by the present model also shows a decreasing trend during combustion, but with a long tail,and the reason for the greater decrease in the burning rate in the combustion stage,compared to the single particle case,is that the evaporation rate is reduced due to the decrease of the aluminum vapor concentration gradient in the fuel-rich flame. In the present work, a numerical model for describing the interphase heat transfer, phase change, homogeneous and heterogeneous reaction, oxide cap growth and radiation processes involved in the conversion of micron-sized aluminum particles is proposed. The model is employed to simulate the combustion of single aluminum particles with varying diameters and an aluminum Bunsen flame in the framework of the Euler-Lagrange method. A detailed analysis of the combustion process of single aluminum particles is conducted, in which the consumption rates of aluminum due to HSR and evaporation,as well as the heat release rates due to the various sub-models are presented.The predictions of combustion time of single aluminum particles agree well with available empirical trends for particles with diameters larger than 5 μm, while the prediction gap for smaller particles is noticeably reduced by using a model for the transition regime of interphase heat transfer. The double-front structure of the experimental aluminum Bunsen flame is reproduced well in the present simulation,and the predicted temperature distribution of the flame is consistent with the experimental measurements.By comparing the evolution of the particle burning rates during combustion,it is found that the burning rates obtained from the empirical correlations deviate from the rate predicted by the present Euler-Lagrange simulation. This is because the oxygen concentration and gas temperature required for the correlations are taken from the Eulerian cell surrounding the particles,which results in an underestimation of the particle burning rate in the combustion stage, especially for particles in a fuel-rich environment. The presented generalized modeling framework is unaffected by the limits of empirical correlations and tailored to simulations of aluminum particle suspension flames.The model shall be used to predict solid rocket engine combustion in future work, which will require further extensions to consider the complex operating conditions therein. The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. This work was supported by the National Natural Science Foundation of China (No. 51706241), Hunan Provincial Natural Science Foundation of China (Nos. 2020JJ4665 and 2021JJ30775), and Hunan Provincial Innovation Foundation for Postgraduate,China(No.CX2019-0050).The support provided by China Scholarship Council (No. 201903170201) during the visit of Jiarui Zhang to University of Stuttgart is gratefully acknowledged.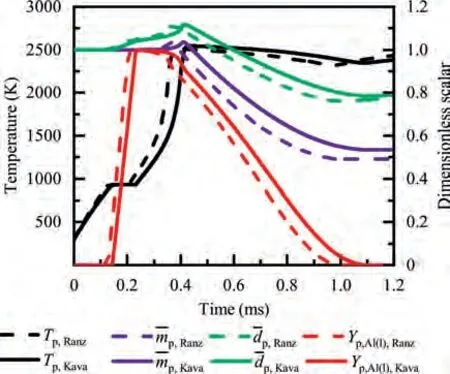

4.2. Aluminum Bunsen flame

5. Conclusions
