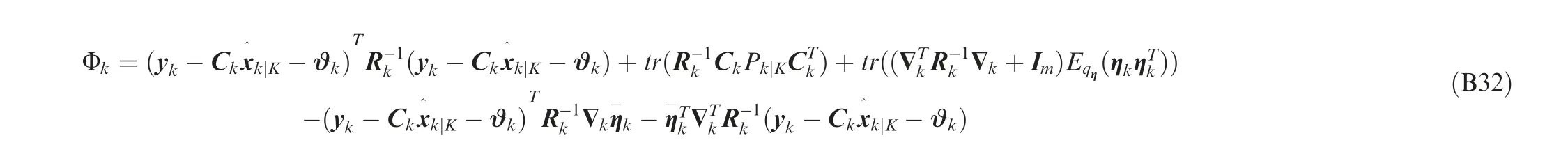Joint parameter and state estimation for stochastic uncertain system with multivariate skew t noises

Shuhui LI, Zhihong DENG, Xioxue FENG,*, Ruxun HE, Feng PAN,b

a School of Automation, Beijing Institute of Technology, Beijing 100081, China

b Kunming-BIT Industry Technology Research Institute INC, Kunming 650106, China

KEYWORDS Estimation methods;Non-Gaussian noise;Target tracking;Uncertain systems;Variational principles

Abstract Due to the pulse interference, measurement outliers and artificial modeling errors, the multivariate skew t noise widely exists in the real environment. However, to date, little attention has been paid to the state estimation for systems in which the process noise and the measurement noise are both modeled as the heavy-tailed and skew non-Gaussian noise. In this paper, the multivariate skew t distribution is utilized to model the heavy-tailed and skew non-Gaussian noise.Then a probabilistic graphical form of the multivariate skew t distribution is given and proved.Based on the probabilistic graphical form,a hierarchical Gaussian state space model for stochastic uncertain systems is proposed,which transforms the estimation problem for systems with the heavy-tailed and skew non-Gaussian noises into the one with a hierarchical Gaussian state space model.Next,given the designed Gaussian state space model,the robust Bayesian filter and smoother based on the variational Bayesian inference are proposed to approximately estimate the system state and the unknown noise parameters. Furthermore, the complexity analysis together with the controllability and observability for stochastic uncertain systems with multivariate skew t noises is given. Finally,the simulation results of the target tracking scenario verify the validity of the proposed algorithms.©2021 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

Non-Gaussian noise widely exists in the real environment due to the pulse interference, measurement outliers and artificial modeling errors.It brings a huge challenge to derive an analytical estimator because there is neither a general mathematics formula nor a closed and free form for the posterior Probability Density Function (PDF). For this purpose, particle filters are often used to deal with the state estimation problem by the sequential importance sampling. But the number of particles increases exponentially with the state dimension, which undoubtedly adds the computation complexity and limits its application in the real-world scenarios.To achieve the state estimation with less complexity and higher accuracy, many methods have been proposed for the non-Gaussian estimation issues. One technique is the Huber filter that is a generalized maximum-likelihood estimation method.The Huber cost function is used to ensure that the residual error of the filter is bounded so that the influence of non-Gaussian noise on the Kalman Filter (KF) can be reduced.And the Huber’s Filter has been successively extended into many versions, for example, a new Robust CKF (RCKF) algorithm by combining the Huber’s M-estimation theory with the classical CKF, a Robust Unscented Kalman Filter with unknown noise statistics, and a robust diffusion Huber-based least mean square algorithm with adjustable thresholds.Although the Huber Filter and its extensions can reduce the effects of non-Gaussian noise on the estimators via the cost function, the Huber cost function cannot identify whether the obtained measurement contains any useful information. Besides, multiple model adaptive estimators (for example, Gaussian Mixture Filtersand Interactive Multiple Models) are alternative methods to deal with the non-Gaussian noise, which require the precise ‘model dictionary’ to represent possible system model sets.However,the prior information is not always available.Another newly emerging estimator is the correntropy criterion based KF, which adopts the maximum/minimum correntropy criterions to exclude the non-Gaussian noise.However, it is difficult to select an approximate kernel bandwidth to capture the second and higher order statistics information, which extremely limits the estimation accuracy.

Recently,a Variational Bayesian(VB)inference method,as a promising calculation technique,is attracting more and more attention, for an efficient inference is conducted to approximate the joint posterior probability distribution of the state and unknown parameters by virtue of the mean field theory.In other words, a solution is developed by converting the intractable posterior probability density function into a tractable factored form. In this way, it can achieve a trade-off between mathematical rigor and computational load.So many VB estimators have been proposed to solve the heavy-tailed non-Gaussian noise, e.g., the Multivariable Student T Distribution (MTD) based Robust Bayesian Filtersand Smoothers, Normal-Gamma-Inverse Wishart Distribution based Estimators, Gaussian-Student’ Mixture Filters,and Gaussian Scale Mixture Estimators. Thereinto, a fast VB multi-sensor data fusion method based on the MTD was designed for the time-varying linear system with unknown and heavy-tailed measurement noise.The VB filters based on the MTD for the linear system were extended to the smoother for nonlinear systems with heavy-tailed process and measurement noises.Later, Refs.respectively expanded the current MTD based VB estimators to the novel estimators for the Normal-Gamma-Inverse Wishart Distribution, Gaussian-Student’ Mixture Distribution and Gaussian Scale Mixture Distribution. Except for Refs., the above designed estimators can hardly be utilized into the estimating framework of the general heavy-tailed non-Gaussian noise,which extremely limits their applications. Besides, most existing works approximated the posterior PDF of the state as a Gaussian PDF with adaptively selected covariance matrix via maximizing the Evidence Lower Bound (ELB).Note that besides the above VB estimators, there still exit some other estimating methods for the heavy-tailed non-Gaussian noise.A novel Kullback-Leilber Divergence (KLD) based Student t estimator was devised, which approximated the posterior PDF of the state as the Student’s T-PDF.Different from Ref., a statistical similarity measurement based robust estimator is proposed for the general heavy-tailed non-Gaussian noise, which was derived by maximizing the designed cost function based on the generalized correntropy.

Except for the heavy-tailed property, the real system noise also has the skew property. For example, in the autonomous underwater vehicle co-location system, the Doppler velocity outliers and the acoustic ranging outliers will induce the heavy-tailed and skew non-Gaussian noises, respectively.While tracking an agile target that is observed in clutter, the heavy-tailed and skew process noise may be induced by severe maneuvering, and the heavy-tailed and skew measurement noise may be induced by measurement outliers from unreliable sensors.For the Ultra-Wide Bandwidth(UWB)indoor positioning system, the multipath effect will also induce the heavy-tailed and skew non-Gaussian noises. Given the time of flight based UWB measurement experiment, Fig. 1 shows the histogram of the range measurement error, whose PDF is respectively fitted as the Univariate Gaussian Distribution(UGD), Univariate Student T Distribution (UTD) and Univariate Skew T Distribution(UST)by the maximum likelihood method. Bayesian Information Criterion (BIC)values for 3950 data points are 15,737 for the UGD, 14,470 for the UST, and 14,758 for the UTD. According to the BIC, the UST can fit the data better than the UGD and UTD, for the latter only considers the heavy-tailed property. However, the UST distribution can simultaneously take the skew and heavy-tailed property into account.Nurminen et al.firstly carried out the research on this issue and simultaneously pointed out that the skew t distributioncould model the heavy-tailed and skew non-Gaussian noise better than the symmetric Student t distribution via the BIC. Therefore, the measurement outlier based on the heavy-tailed (high-kurtosis)and asymmetric (skewed) property was firstly modeled as the univariate skew t distribution, and the corresponding filter and smoother have been proposed to jointly estimate the state and unknown parameters of the noise.Later,Nurminen et al.extended the results of Ref., and a VB-based posterior approximation with coupled location and skewness variables was used to reduce the error caused by the variational approximation.A time-varying UST distribution was adopted to match the statistics of the measurement noise via the VB technique, and simultaneously update the noise statistics and the state.Although the above methods based on the UST distribution are proposed to model the heavy-tailed and skew noise, the real physical system is generally high dimensional.It should be noted that the cross-covariance of multidimensional variables is not negligible, for ignoring the crosscovariance will inevitably lead to the imprecise covariance and further affect the estimation accuracy. Thus, the above methods based on the UST distribution cannot be directly applied to multidimensional systems. That is to say, it is more appropriate to adopt the Multivariable Skew T (MST) Distribution to model the heavy-tailed and skew non-Gaussian noise.

Fig. 1 Measurement error histogram and maximum likelihood fits of some probability distribution families.

Therefore,the heavy-tailed and skew non-Gaussian noise is firstly modeled as the MST distribution in this paper. And a Hierarchical Gaussian State-Space Model (HGSSM) based on the MST distribution is proposed by fully utilizing the statistical character of the noise. Based on the HGSSM, the VB technique is adopted here to propose a novel MST-based VB Filter (PSTVBF). Moreover, the VB technique and the design principle of the smoother are melted to propose a new MSTbased VB smoother(PSTVBS).The main contributions of this paper are concluded as follows:(A)The process and measurement noises are firstly modeled as the MST distributions that are more general and can better capture the heavy-tailed and skew properties of the received signals than the MTD or Gaussian distributions. And the Probabilistic Graphical Model(PGM) of the MST distribution is described and proved. (B)The proposed HGSSM based on the PGM can transform the estimation problem for the system with heavy-tailed and skew non-Gaussian noises into the one with the HGSSM,which can extremely simplify the design of the estimators.(C) Based on the HGSSM, the VB approach and the smoothing method, the designed PSTVBF method and PSTVBS method can provide more reliable state estimations by adaptively learning the statistics properties of the MST distribution.(D) The controllability, observability and complexity analysis for the stochastic uncertain system discussed are given here.

The rest of this paper is organized as follows:Section 2 presents the problem formulation. The PSTVBF method and the PSTVBS method for the discrete linear system with the heavytailed and skew non-Gaussian noises are presented in Section 3.Simulation results for the performance comparison are presented in Section 4, and the conclusion is finally drawn in Section 5.

2. Problem formulation

In this section,a brief review of the MST distribution is firstly given,which is a new class of multivariate skew elliptical distributions introduced by Sahu et al.A random vector Y is said to follow a MST distribution, denoted by Y ～St（ε，Ξ，Π，ν）,if it can be represented by

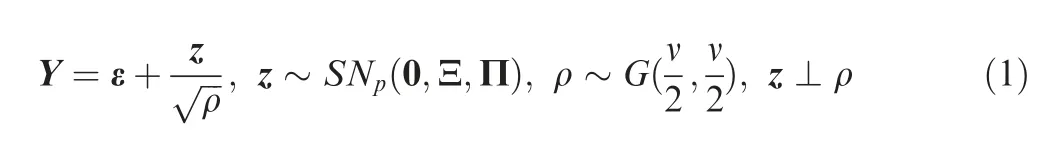
where ε， Ξ， ν and Π denote the location vector, the scale covariance matrix, the Freedom Degree (FD) and the skew matrix, respectively. Thereinto, a random vectorzfollows a pvariate Skew Normal (MSN) distribution SN（0，Ξ，Π） .A random value ρ obeys a Gamma distribution G（α，β） with parameters α and β, whose meaning is α/β . The symbol ‘‘⊥”indicates the independence. Note that the distribution of Y can reduce to the MTD t（ε，Ξ，ν） as Π=0 and to SN（ε，Ξ，Π） as ν →∞.

Considering that the stochastic system in practical applications suffers from sensor outliers,multipath effects of acoustic channels,and sharply changing environment,both the process and the measurement noises are subject to the heavy-tailed and skew noise modeled by the MST distributions.Thus,the following discrete linear system with the MST noise is considered:

However, different from the design of Gaussian filter and smoother, the heavy-tailed and skew properties of non-Gaussian noise bring some special challenges, which are listed as follows:

(1) The complex statistical properties of the MST noise make it intractable to obtain the analytical solutions for the posterior PDF p（x|y） and the smoothing PDF p（x|y）via Eqs.(4)-(5),because neither a general mathematical formulation nor a closed form exists for a non-Gaussian posterior PDF.

(2) Considering that the expression of the real MST distribution is always complex, the deeply coupling relationship exists between the state and the model parameters of the MST distribution, which makes it tough to design the estimators.

(3) The multidimensional characteristics of the MST noise make it difficult to extend the current state estimators based on the UST distribution to the cases of the MST noise due to the unknown cross-covariance among the UST noises.

Based on the above discussion, the VB inference can perform the efficient approximation for the posterior inference at a relatively low computation cost with an acceptable accuracy.To this end,the aim of this paper is to derive a new estimation method via the VB method based on the received measurements.

Remark 1. Due to the heavy-tailed and skew properties of the non-Gaussian noise,many estimators are invalid or inaccurate to calculate optimal solutions of Eqs.(4)-(5). For example, particle filters will suffer from a huge computational burden because of vast Monte Carlo sampling particles.Multiple model filters fail to obtain the accurate estimation results for the adequate models are not always available to approximate the true posterior distribution.The Huber filters based on the cost function or the maximum/minimum entropy filters will be ineffective due to the lack of an approximate kernel bandwidth.Except for particle filters,the above several types of estimators can hardly achieve the satisfying estimation accuracy for they failed to update the posterior PDF of the state via the high order statistical information of the noise.Although most of the current VB estimatorstogether with the other novel estimatorscan use the high order statistical information of the noise to update the posterior PDF of the state,they are only effective for the heavy-tailed non-Gaussian noise,for they do not consider the skew properties of non-Gaussian noise. Although Refs.are appropriate for the heavy-tailed and skew non-Gaussian noise via the VB approach,they are only suitable for the univariate heavytailed and skew non-Gaussian noise and can hardly be expanded to the multivariable cases, for the cross-covariance of the multidimensional noise distribution is always unknown.

3. Robust PSTVBF and PSTVBS for stochastic systems with heavy-tailed and skew noises

In this section, two robust estimators for discrete linear systems with the heavy-tailed and skew non-Gaussian noises are designed. Firstly, the MST distribution is adopted to model the heavy-tailed and skew properties of the non-Gaussian process and measurement noises. In order to conduct the VB inference,an equivalent PGM of the MST distribution is given and proved.Based on the equivalent PGM,an HGSSM is proposed,which transforms the estimation problem for the system with the heavy-tailed and skew non-Gaussian noises into the one with an HGSSM. Secondly, based on the HGSSM, the VB approach is utilized to propose the PSTVBF method and the PSTVBS method, which both can jointly estimate the system state and unknown parameters of the HGSSM via an approximation of the true posterior PDF. Finally, the complexity analysis together with the controllability and observability for the stochastic uncertain systems with the MST noises is derived.

3.1. Hierarchical Gaussian state space model based on MST distribution

Firstly, a theorem about an equivalent expression of the MST distribution is described, which is necessary for the derivation of the hierarchical Gaussian state space model in the next section.

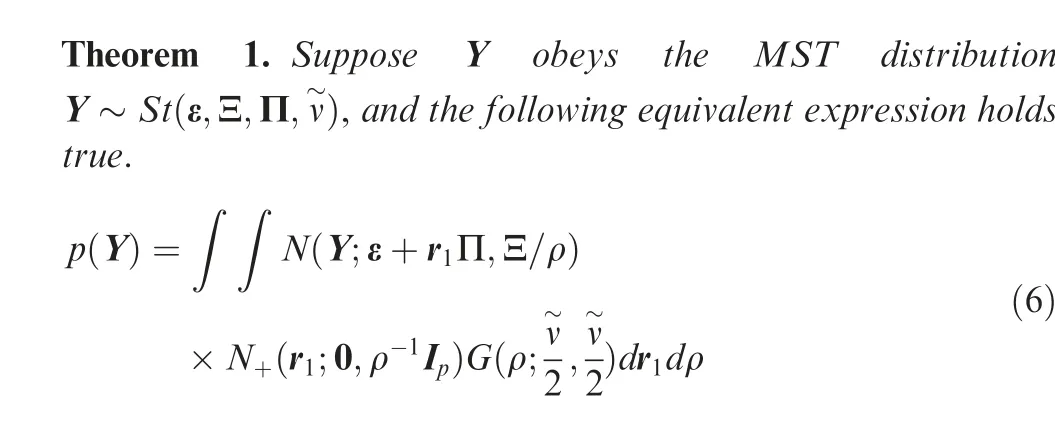
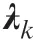
Remark 3. The proposed work can deal with heavy-tailed and skew noises at the same time. The detailed reason is that the PSTVBF and PSTVBS assume a nominal cross-covariance and simultaneously introduce the shape parameters μand ηas well as the mixing parameters φand φ,which can regulate the nominal cross-covariance to approximate the true one. In other words,the shape parameters μand ηcontrol the skewness of non-Gaussian noise (namely the mean value), and the mixing parameters φand φcan regulate the tailed properties(namely the co-variance). When the shape parameters μand ηbecome small,the left tail of the non-Gaussian noise is longer than the right one.On the contrary,the right tail is long.In this way, the shape parameters can adjust the skew properties. Similarly, when the mixing parameters φand φare small, the tail of non-Gaussian noise will be heavy. Since these unknown parameters and the state are stochastic and with the assumed prior distributions, the VB method can infer and learn the approximate posterior probability density functions of the state and unknown parameters. In this way, the state and unknown parameters can be refreshed.

3.2. Derivation for PSTVBF method

θbelongs to the set Θ, namely θ∈Θ, which represents any element in the set Θ.Let Θbe the subset of the set Θand have all the elements in Θexcept for θ, i.e.,θ∪Θ=Θ. In order to choose the optimal factorized

3.3. Derivation for PSTVBS method

The key of the Bayesian filter aims at computing the state estimation by the measurements obtained before and at timek,but the Bayesian smoother also uses the future measurements to calculate its estimate. In a sense, the latter can fully take advantage of the measurement information and achieve the better estimation performance. Hence, in this part, a robust smoother for the system with the heavy-tailed and skew non-Gaussian noise is designed. Similar with the design of the PSTVBF method in Section 3.2, the state-space model with heavy-tailed and skew noise can be transformed into an HGSSM including Eq.(13) and Eqs.(19)-(20). Correspondingly, the smoothing issue with heavy-tailed and skew noise can be transformed into the one for the equivalent Gaussian system. Based on the HGSSM, the VB approach and the smoothing technique are used to jointly estimate the unknown state x, the shape parameters μand ηtogether with the mixing parameters φand φ.

Combine the state x,the unknown shape parameters μand ηas well as the unknown mixing parameters φand

Table 1 Implementation of PSTVBF method.

Table 2 Implementation of PSTVBS method.

The PSTVBF and PSTVBS have the following advantages.Firstly, compared with the current methods based on the MTD, the PSTVBF method and the PSTVBS method do not need additional distributions to model non-Gaussian noise parameters, consequently reducing complexity of the method design. Secondly, compared with the methods based on the UST distribution,the proposed methods here have a wider range of applications for the practical system noise is always high-dimensional and obeys the multivariate distribution.Once the process noise is subject to the Gaussian distribution and the measurement noise is subject to the UST distribution, the current methodswill be the special cases of the proposed algorithms here.

3.4. Analysis of controllability, observability and complexity

The controllability and observability of stochastic systems are two important concepts in the filter field. The stochastic observability refers to the ability that moves the state to the desired destinations.The stochastic controllability means whether the output measurements can accurately determine the system state.The sufficient condition of the controllability and observability for linear stochastic systems with the MST noise are given in the following theorem.

Theorem 3. For any given scale covariance matrix Ξ, skew matrix Π, freedom degree satisfying ν ≥3 and rank（A）=n,the covariance of the MST noise is bounded, and the linear stochastic systems with the MST noise in Eqs.(2)-(3) are observable and controllable.

The detailed proof can be seen in Appendix C.

The most efficient way to analyze algorithm complexity is to count its floating-point operations. The Equivalent Flop(EF) complexity for an operation is defined as the number of the flops that results in the same computational time as the operation.Based on Ref., the EF complexities for some common matrix operations are summarized in Table 3.According to the PSTVBF method in Table 1, the EF complexity for each stage at timekis shown in Table 4, where L and K respectively represent the number of the fixed-point VB iteration and the simulation step. n and m are the dimensions of the state and the measurement, respectively.

Since Table 4 shows the EF complexity of single equations,they do not consider the number of the fixed-point VB iteration L together with the simulation step K during the implementation of the whole algorithm. Therefore, when the number of the fixed-point VB iteration and the simulation step are respectively L and K,the total EF complexity for the whole PSTVBF method in Table 1 is given by

Table 3 EF complexity of some common matrix operations38.

Table 4 EF complexity of PSTVBF method for each stage at time k.

4. Numerical simulation

The performance of the PSTVBF and PSTVBS methods is illustrated by a target tracking scenario in this section.The target moves in a horizontal plane and undergoes a constant turn maneuver. The state transition matrix Aand observation matrix Care respectively given by

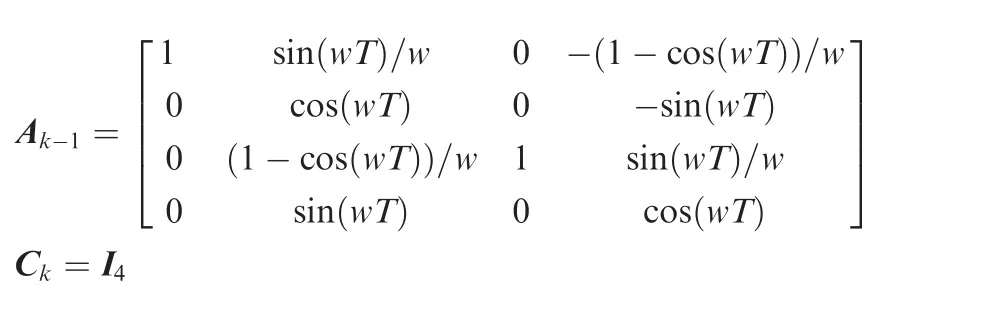
where Iis the four-dimensional identity matrix, the sampling time is T=1s, and the turn rate is w=3rad/s. The targetstate is defined as x=［x，y， ˙x， ˙y］, where x，y， ˙xand ˙ydenote the positions and corresponding velocities in Cartesian coordinates. The process noise wand the measurement noise vare generated by the MST distribution St（2，I，I，3） and St（1，0.5×I，I，3）, respectively. And the initial value of the true state xis set as x=［10，0，10，0］.

Table 5 EF complexities of some equations in PSTVBS method.

To verify the effectiveness of the PSTVBF and PSTVBS methods, the Skew T based Variational Bayesian Filter(STVBFm)and Smoother(STVBSm) for the heavy-tailed and skew measurement noise are adopted for comparison, where the heavy-tailed and skew measurement noise is modeled as the univariate skew t distribution. For the heavy-tailed and skew measurement noise is one kind of non-Gaussian noises, several methods are adopted here for comparison,which can deal with the non-Gaussian noises well,for example,the KF with a measurement validation Gating (KFG), the Kalman Filter based on Maximum Correntropy Criteria(KFMCC),the Student T Variational Bayesian Filter(TVBF)and Smoother(TVBS)with unknown measurement covariance, and the Rauch-Tung-Striebel Smoother with a Gating(RTSSG).Besides,the approximate Bayesian Smoother with unknown Process and Measurement noise covariances(SPM)for it can deal with unknown noise parameters.And the VB iterations of PSTVBF, PSTVBS, SPM, TVBF,TVBS, STVBFm and STVBSm methods are 10, 10, 10, 10,10, 10 and 10.

To compare the performance of the existing methods and the proposed algorithms, the Root Mean Square Errors(RMSEs),the Averaged RMSEs(ARMSEs)and the Averaged Absolute values of position and Velocity Biases (AAVBs) are chosen as performance metrics.The RMSE, ARMSE and AAVB of positions are respectively defined as

The true and estimated trajectories obtained from the above estimators and the proposed algorithms in a single Monte Carlo run are shown in Fig.2.The RMSEs of the position and velocity from the existing estimators and the proposed algorithms are respectively shown in Figs. 3 and 4.And the corresponding ARMSEs and AAVBs of the position and velocity are given in Table 6, respectively.

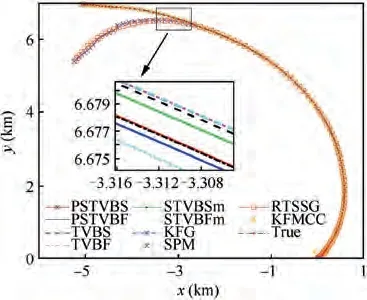
Fig. 2 True and estimated trajectories of target.

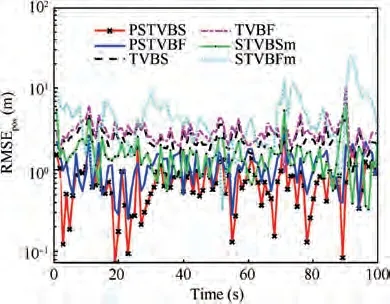
Fig. 3 RMSE comparison of position.

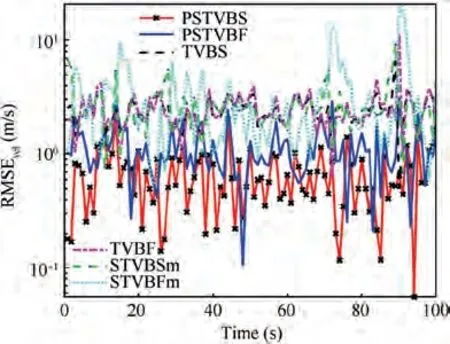
Fig. 4 RMSE comparison of velocity.

It can be seen from Fig. 2 that the estimated trajectories from the PSTVBS and PSTVBF methods are much closer to the true trajectory compared with the other eight algorithms.Besides, Figs. 3-4 show that the PSTVBF and PSTVBS have smaller RMSEs than other eight comparison algorithms. For simplification, the RMSEs of the KFG, SPM, RTSSG and KFMCC methods are omitted in Figs. 3-4 because there are much bigger estimated fluctuations. The main reason is that the KFG uses the measurement validation gating based on the χdistribution to eliminate the outliers, but the real measurement noise is with the MST distribution. In this case, the measurement validation gating seriously deviates from the realnoise distribution so that the filter divergence occurs.Different from the KFG method, the SPM method assumes that both the process and measurement noise covariances obey unknown inverse Wishart distributions.Similar with the KFG method,it still does not get rid of the traditional filter framework. However,this does not conform with the system with non-Gaussian noise discussed here. Hence it is inevitable to induce the filter divergence. Similarly, although the RTSSG method adopts the smooth strategy and the validation gating to eliminate the heavy-tailed and skew noise, the Gaussian noise assumption still makes it lose the necessary information and bring in the big estimation error because the real system is with the MST noise. And the KFMCC method generally utilizes the Gaussian kernel function to estimate the state, which is inconsistent with the real process and measurement noises.Therefore, it is inevitable to generate a big estimation error.For the TVBF and TVBS methods, they are both designed for the system with the MTD which contains less skew information. In other words, the statistics properties of the supposed noise in the TVBF and TVBS methods deviate from the true one, which will produce large fluctuations in the estimation results.Although the STVBSm and STVBFm methods use the UST distribution to model measurement noise, the assumptive process noise is inconsistent with the real one. To sum up, the statistical property of the assumptive noise is different from the real MST distribution,which makes the above eight comparison methods have low estimation accuracy.Moreover, Table 6 also shows that the position ARMSEs of the PSTVBS and PSTVBF methods are respectively 51.4%and 34.2% less than that of the other eight comparison methods. And the velocity ARMSEs of the PSTVBS and PSTVBF methods are respectively 76.5% and 59.2% less than that of the other eight comparison methods. The PSTVBS and PSTVBF methods also achieve less AAVBs than the other eight comparison methods.

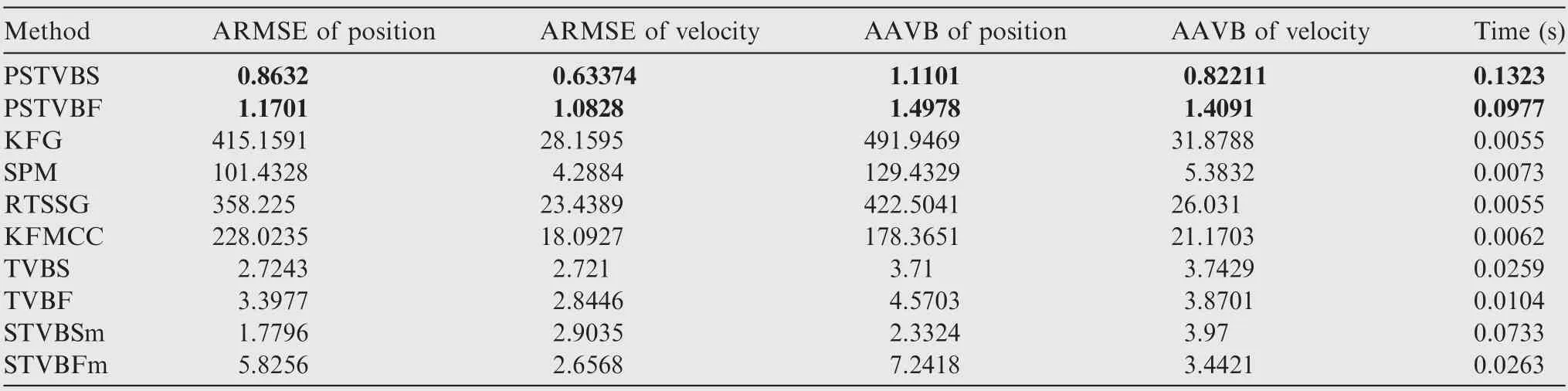
Table 6 Performance comparison of different methods.

The computational costs of eight comparison methods are compared in Table 6. The total EF complexities of eight comparison methods are given.

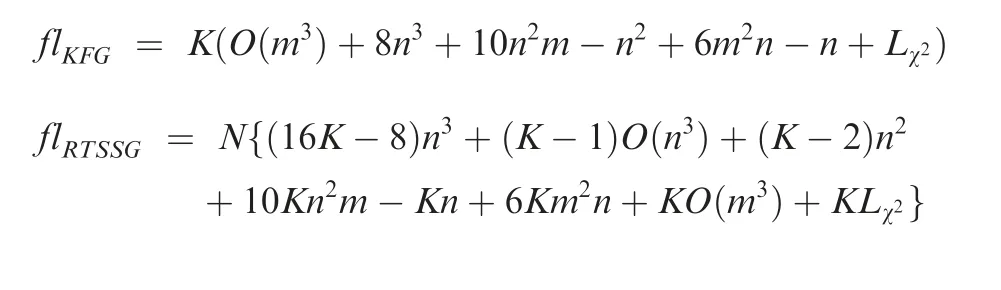
5. Conclusions

In this paper, the PSTVBF and PSTVBS methods are proposed for the system with heavy-tailed and skew noises.Firstly, the MST distribution is adopted to model the heavytailed and skew properties of the non-Gaussian process and measurement noise. In order to conduct the VB inference,the PGM of the MST is given and proved. Based on the PGM, an HGSSM for stochastic uncertain systems is proposed, which transforms the estimation problem for the systems with heavy-tailed and skew non-Gaussian noises into

Appendix A. Derivation for PSTVBF

In order to conveniently derive the expectations for the cyclic iterations of the VB filter,the log of the joint filtering posterior is necessary,which is given by(the iteration stepiis omitted for simplicity)

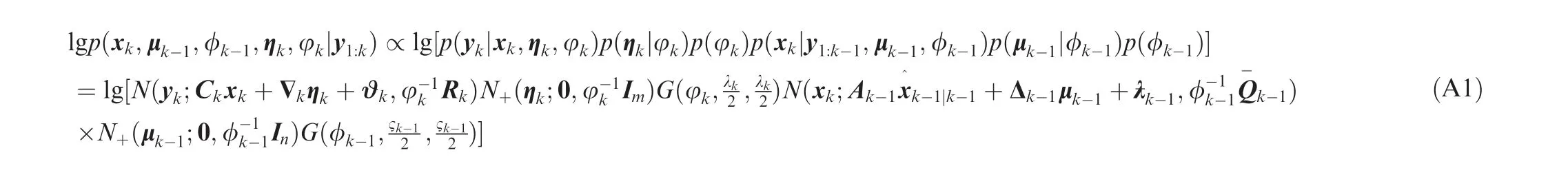
the one with an HGSSM. Secondly, given the HGSSM, the PSTVBS and PSTVBS methods based on the VB approach

(1) Derivation for lgq（x）

Based on Eq.(22) and Eq.(A1), let θ=xand we have

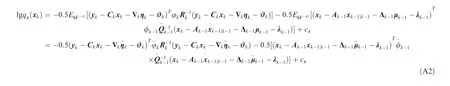
are designed to jointly estimate the system state and unknown parameters.Thirdly, the complexity analysis together with the controllability and observability for stochastic linear systems with the MST noise is given. Finally, the simulation results of the target tracking scenario verify the effectiveness of the proposed methods.In the future,some sampling methods that can extend the proposed algorithms to nonlinear systems will be considered. Besides, the design of robust multi-sensor consensus filters based on the MST distribution will be discussed.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China (Nos.61603040 and 61433003), Yunnan AppliedBasicResearchProjectofChina(No.201701CF00037), and Yunnan Provincial Science and Technology Department Key Research Program (Engineering), China (No.2018BA070).

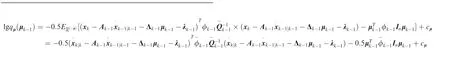
where