Adaptive cubature Kalman filter with the estimation of correlation between multiplicative noise and additive measurement noise

Quno GE, Zhonghng MA, Jingln LI, Qinmin YANG,*, Zhnyu LU,Hong LI

a School of Electronics and Information Engineering, Tongji University, Shanghai 201804, China

b Institute of Systems Science and Control Engineering,School of Automation,Hangzhou Dianzi University,Hangzhou 310018,China

c State Key Laboratory of Industrial Control Technology, and the College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, China

d Jiangsu Key Laboratory of Meteorological Observation and Information Processing, Nanjing University of Information Science and Technology, Nanjing 210044, China

e Chinese Flight Test Establishment, Xi’an 710089, China

KEYWORDS Adaptive CKF;Correlated noise;Estimation accuracy;Multiplicative noise;Performance analysis;Target tracking

Abstract Mobile robots are often subject to multiplicative noise in the target tracking tasks,where the multiplicative measurement noise is correlated with additive measurement noise. In this paper,first, a correlation multiplicative measurement noise model is established. It is able to more accurately represent the measurement error caused by the distance sensor dependence state. Then, the estimated performance mismatch problem of Cubature Kalman Filter (CKF) under multiplicative noise is analyzed. An improved Gaussian filter algorithm is introduced to help obtain the CKF algorithm with correlated multiplicative noise. In practice, the model parameters are unknown or inaccurate, especially the correlation of noise is difficult to obtain, which can lead to a decrease in filtering accuracy or even divergence.To address this,an adaptive CKF algorithm is further provided to achieve reliable state estimation for the unknown noise correlation coefficient and thus the application of the CKF algorithm is extended. Finally, the estimated performance is analyzed theoretically,and the simulation study is conducted to validate the effectiveness of the proposed algorithm.

1. Introduction

IN recent years, researches on mobile robot target tracking have been rapidly developed.In order to improve the positioning accuracy of the robot, Kalman filtering is often used to estimate the state. In general, a nonlinear mathematical model with random disturbances is established for related problems. Considering the fact that traditional Kalman filtering can only deal with linear problems, many nonlinear filtering methods have been proposed. Gaussian filter algorithm is widely used in nonlinear Gaussian systems, which is able to provide a filtering framework for the state estimation, such as Unscented Kalman Filters(UKF)and Cubature Kalman filters (CKF). Comparatively, CKF is recognized to have higher estimation accuracy. However, a fact cannot still be avoided,namely,the used model in the filtering process is generally mismatching to the practical system because of modeling error, linearization and non-Gaussian noise, inaccurate crosscorrelation formulation and so on. Accordingly, the adaptive filtering has been presented to obtain better accuracy and more robust estimation. Recently, many adaptive filtering methods have been proposed ceaselessly for different application background.As a result,the application study has been further advanced on the adaptive Kalman filtering. The realization of CKF is often based on the premise that the system process noise and measurement noise are additive white Gaussian noise.However,there is not only additive noise but also interference of multiplicative noise in the actual engineering practice. Multiplicative noise is usually caused by undesired channels,including jitter or vibration during the measurement,and attenuation of signal energy. Especially in target tracking, the sensor measurement noise increases with distance. The filtering estimation accuracy will inevitably decrease, if the multiplicative noise model is not taken into consideration. Thus, how to achieve a satisfactory performance of state estimate in target tracking in presence of the multiplicative noise is of great importance.

In the early stages, state estimation or filtering with multiplicative noise was generally discussed in underwater acoustic communications, and some improved linear Gaussian Kalman filters and fusion methods have been established for different applications. The above work only focused on the estimator design under known statistic characteristics of multiplicative noises and non-relation to other noises.Afterwards,for more complex systems with multiplicative measurement noise and correlated additive noises, state estimation has been further studied.In the existing literature,two approaches have been introduced to solve the multiplicative noise problems. The first is to adaptively modify the filtering model with certain approximation methods,and the other is to obtain a filter algorithm with multiplicative noise by mathematical derivation. For the first method, a Kalman filtering algorithm for maximum likelihood estimation is introduced in Ref. [23]to solve the target tracking problem under the multiplicative noise model. Experimental results have also verified that the multiplicative noise cannot be ignored in such a distance measuring system.In Ref.[24],a Generalized Iterative Kalman Filter (GIKF) with state-dependent multiplicative measurement noise has been proposed, which obtains a higher estimation accuracy than the Generalized Extended Kalman Filter(GEKF)and EKF.In addition,an iterative MEKF filter algorithm is discussed in Ref. [12], which can effectively overcome the effects of multiplicative noise in the satellite attitude estimation. The idea of Levenberg-Marguard (LM) optimization is utilized to improve Iterative Extended Kalman Filter(IEKF) in Ref. [13], and a modified LM-IEKF algorithm for adaptive measurement noise is then proposed,which can avoid the filtering accuracy decrease due to multiplicative noise.The second category of methods is relatively less studied. In Ref.[14],a generalized Kalman filter method is proposed in the scenario of wireless sensor networks. By using the definitions of mean, covariance and cross-covariance, the state estimation value and covariance of Kalman filter with multiplicative noise are presented to extend the applications of Kalman filtering.

Actually, there is correlation on multiplicative noise because of complex signal sampling and transmission. Unfortunately, the correlation is not considered for most of current Kalman filters. In Ref. [25], a distributed estimation of a nonlinear system has been studied by considering the correlations between multiplicative noises and process/measurement noises.But,it supposes that the correlations are known.For practical applications, it is very difficult to obtain accurately the correlation coefficients in advance. Additionally, the correlation coefficient is very important because it is closely dependent on performance evaluation and analysis of the Kalman filters.Accordingly,dynamically estimating the correlation coefficient becomes an essential way to improve estimation performance.Therefore,in this work,a mobile robot tracking problem using distance sensor is studied,where the data measured by the distance sensor are contaminated by the distance-dependent multiplicative and additive measurement noises.To overcome this problem, a nonlinear correlation multiplicative measurement noise model is firstly built. A nonlinear estimator is subsequently designed for the multiplicative noise correlation system. In order to improve the tracking ability, an inaccurate model is further considered, where the correlation coefficient is no longer accessible and is estimated by using the covariance matching method.An adaptive CKF algorithm with correlated multiplicative noise is thus provided.

The rest of this paper is organized as follows. Section 2 gives the problem formulation. In Section 3, the influence of multiplicative noise on the estimated performance of CKF is analyzed first. Then the Gaussian filter with correlated multiplicative noise is designed. Finally, the CKF algorithm with correlated multiplicative noise is given. For the problem that the noise correlation matrix is unknown, Section 4 proposes a noise correlation adaptive estimation algorithm.In Section 5,the influence of correlated multiplicative noise on the FMSE is analyzed first,and then the influence of the inaccurate correlation coefficient on the filter performance is deeply studied.Simulation examples are provided in Section 6. We conclude this paper in Section 7.

2. Problem formulation

2.1. System description

In the target tracking problem, the measurement error of the distance sensor increases with the distance between the sensor and the target.Moreover,it is assumed that the measured distance value of the sensor is contaminated by distancedependent multiplicative measurement noise, which is correlated to additive noise.

Consider the following discrete-time nonlinear system with multiplicative noise as follows:

2.2. Model conversion

3. Gaussian filter algorithm with correlated multiplicative noise

3.1. Performance mismatch analysis of cubature Kalman filter

When the measurement data of the sensor contain multiplicative noise,it is necessary to establish a model under multiplicative noise. Besides, if additive measurement noise is only considered, it will lead to inaccurate modeling, which further results in a decrease of filter estimation accuracy.

In the filtering process, the estimation error covariance is often used to represent the Mean Squared Error (MSE) of the filter estimation.When only additive measurement noise is considered,based on the basic principle of the Kalman filter,the Filter-calculated MSE (FMSE) is given as follows:

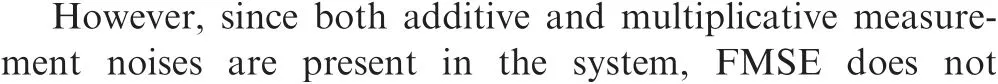
Theorem 1. If the system measurement data contain system state dependent multiplicative measurement noise, one has

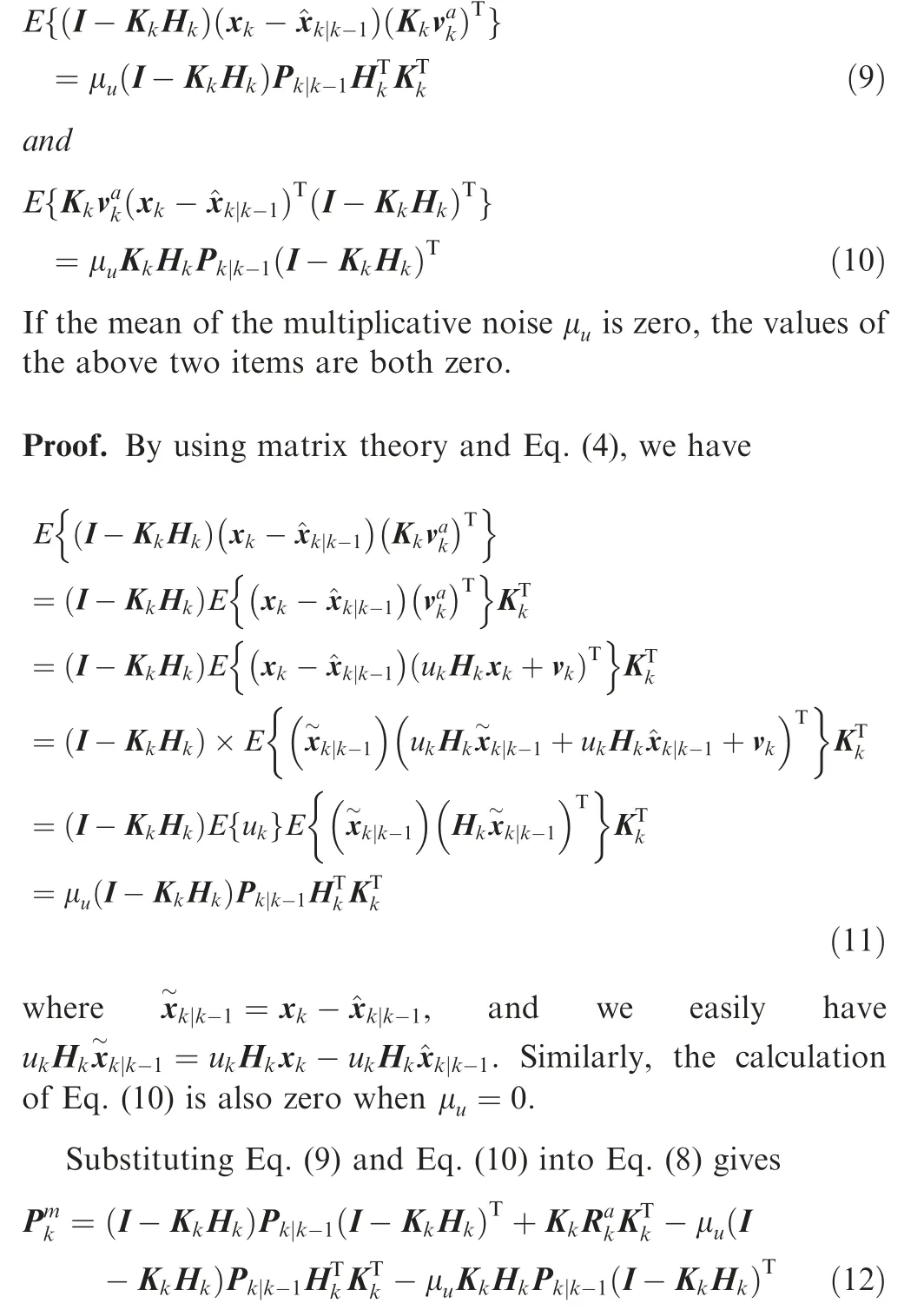
where the superscript （·）represents the true value.

By comparing Eq. (5) with Eq. (12), it can be found that if the CKF is implemented without the considering of the multiplicative noise, FMSE and TMSE do not match with each other and filtering accuracy will be hurt.Therefore,it is necessary to tailor the CKF according to the multiplicative noise model.

3.2. Improved Gaussian filter algorithm

3.3. CKF algorithm with correlated multiplicative noise

CKF is a filtering method proposed in Ref.[6]for dealing with nonlinear systems. In Gaussian filter, it solves the problem of multidimensional Gaussian weighted integration in practical applications,and transforms the integral form into a spherical radial integral form. CKF is constructed with a third-order spherical radial cubature criterion,which uses a set of cubature points to approximate the state mean and covariance of nonlinear systems with additional Gaussian noise, and has higher filtering accuracy. In this paper, CKF can be regarded as an implementation of improved Gaussian filter. A CKF with correlated multiplicative noise will be provided, which enables CKF to deal with the cross-correlation problems,and expands the application range of the CKF.

4. Adaptive CKF algorithm with uncertain multiplicative noise correlation coefficient

4.1. Estimation of multiplicative noise correlation coefficient

The CKF in the case of correlated multiplicative noise is designed in the previous section. However, it is only suitable for the accuracy model.When the model parameters are uncertain, the estimation accuracy of the filter will be reduced.In practical engineering applications, the cross-covariance of multiplicative and additive measurement noises may be unknown or inaccurate.Therefore,based on the principle of covariance matching, this paper estimates the inaccurate noise correlation coefficient in real time through the measurement information.

The CKF innovation is written as

where M is the length of the sliding window. The purpose of Eq. (46) is to calculate an estimated or approximative value of the innovation covariance matrix because the corresponding accurate value cannot be obtained. Meanwhile,this way is also very convenient. It should be noted that if the window width is large, the estimation accuracy could be improved, but the calculation efficiency is poor. By contrast, if the window width is small, the estimation accuracy will be reduced, but the computational efficiency will be improved.

Therefore,the estimated value of the innovation covariance^Pat k-1 time step can be obtained

4.2. Adaptive CKF with correlated multiplicative noise

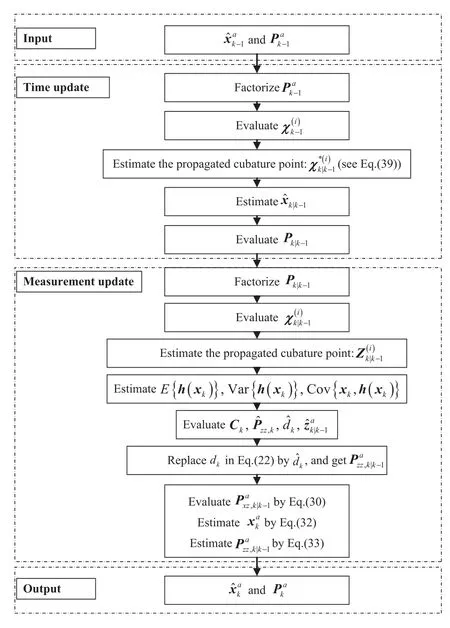
Fig. 1 Flowchart of the proposed adaptive CKF with correlation.

Table 1 Adaptive CKF with correlated multiplicative noise.

5. Performance analysis

In our previous work given in Ref. [28], a deep performance analysis has been presented for the Kalman Filter (KF) with mismatched measurement noise covairance. The work firstly provides a novel analysis way for the KFs performance from engineering viewpoint, which includes IMSE (Ideal MSE),FMSE (Filter calculated MSE), and TMSE (Ture MSE). Secondly, the analysis clearly shows that the standard KF has intrinsic shortcoming, namely, when the used model mismatches to the practical system, the estimation error covariance (FMSE) is easy to lose the ability to accurately measure the estimation accuracy of the KF.For the work given by this manuscript, the estimation system also has the mismatching due to unknown correlation coefficient estimated online.Thereby,it is very important to develop the associated performance analysis in order to evaluate the effect of noise correlation on FMSE and also the relative closeness from FMSE to TMSE, which is supposed to provide guidance for practicers to implement this algorithm.

5.1. Effect of noise correlation on FMSE

Substituting the filter gain Eq. (31) into the FMSE matrix yields

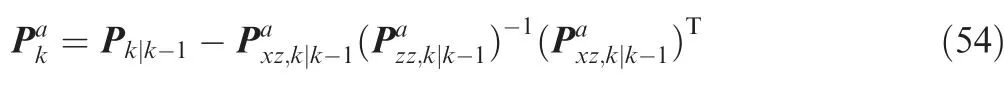
From Eq.(22),it can be seen that the noise correlation can affect the innovation covariance, which also impacts the FMSE. Since D=2dE｛h（x）｝1, it is straightforward that d=0，D=0 if the multiplicative measurement noise is not correlated with the additive one. In accordance with Eq.(28)and Eq.(54),the uncorrelated multiplicative noise FMSE matrix Pcan be expressed as

5.2. Relative closeness from FMSE to TMSE

When the model parameters are not accurate, denote the mismatch on das

We know that when the noise correlation matrix is not accurate, it will lead to the mismatch between the established model and the actual system,and further lead to the mismatch between FMSE and TMSE in the filtering process,and FMSE cannot accurately measure the accuracy of filtering estimation.It is known that, if the noise correlation coefficient is inaccurate, there will be a mismatch between the established model and the actual system,which also leads to a mismatch between the FMSE and the TMSE in the filtering process. In this case,the FMSE will not provide a true measure of the estimation accuracy of the actual filter.In order to make the FMSE closer to the TMSE,this paper proposes an adaptive CKF algorithm with correlated multiplicative noise that adaptively estimates the true noise correlation coefficient ^dand reduces Δdas much as possible.

In the filtering process,let d= ^d.It can be considered that the noise correlation coefficient is relatively accurate, and the deviation of the noise correlation coefficient is Δd=0.Recalling Eq. (67), we have

Based on Eq. (68), it can be concluded that, in the case of inaccurate noise correlation coefficients, the adaptive algorithm will be used to estimate the noise correlation coefficient,which can make the FMSE and the TMSE relatively match,and improve the accuracy of the filter estimation.

5.3. Complexity analysis

Compared with the cubature Kalman filters without the correlation on multiplicative noise, it is necessary to spend more computation to deal with the correlation estimation. A brief analysis is given as follows:

(1) In order to consider factor induced by the multiplicative noise in the filtering process, it is inevitable that the filtering algorithm becomes slightly complex.

(2) It also increases the computation of the proposed filter when considering the correlation on multiplicative noise.

(3) Due to the dynamical estimation of the correlation coefficient given by Eq.(53),the filtering algorithm becomes obviously complex.However,the parameters in Eq.(53)can be taken in recursive computational way.

Thereby,the proposed adaptive CKF has an increasingly complexity. However, for the increasing strong running performance for the current CPU technology and cost, its influence on running efficiency is comparatively small.

6. Simulation examples

In this section,the two-dimensional mobile robot target tracking task will be conducted to verify the effectiveness of the proposed algorithms.All results are over 1000 Monte-Carlo runs.For ease of description, we have simplified the following definition of the tracking algorithm:

Algorithm1. The cubature Kalman filter algorithm.

After a time he began to get hungry, so he decided that he had better try to find his way out of the forest, and perhaps he might have a chance of getting something to eat

Algorithm2. The cubature Kalman filter algorithm with multiplicative noise.

Algorithm3. The cubature Kalman filter algorithm with correlated multiplicative noise.

Algorithm4. The adaptive CKF algorithm with correlated multiplicative noise.

6.1. Tracking model

A Cartesian coordinate system of o-xy is established, where x and y represent the east and north coordinates respectively.Assuming that the sensor is at the origin of the Cartesian coordinate system, the mobile robot performs a motorized turning motion on the flat ground.The nonlinear system model of the target is as follows

where x=［x vy v］, where x and y are the displacement components of the target east and north directions, vand vare the velocity components of the target east and north directions respectively,ω is the target turning angular velocity,and T is the sampling period. The measurement vector is

6.2. Simulation result of Algorithm1

In this scenario,the estimation performance of CKF with multiplicative noise is measured. The results are shown in Fig. 2 and Fig. 3.

From Fig.2,we can conclude that the FMSE of CKF mismatches the TMSE seriously when the multiplicative noise is included in the measurement data.Fig.3 shows the root mean square error of the x and y directions. It can be seen that the estimation accuracy of CKF has diverged.

6.3. Performance comparison of three algorithms

In the second scenario, a comparison study on the estimation accuracy among Algorithm1, Algorithm2, and Algorithm3 is conducted. The corresponding results are plotted in Fig. 4.

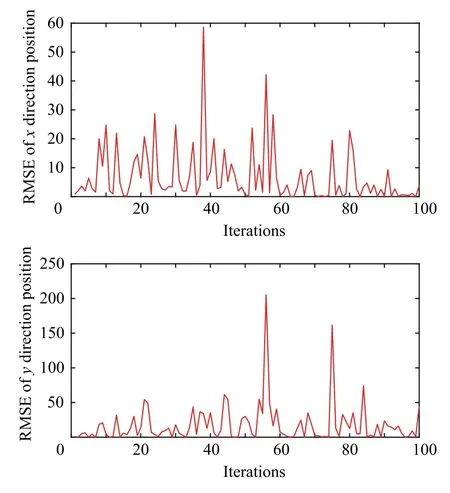
Fig. 3 RMSE of x and y direction position..

As can be seen from Figs.4(a)-(b),the estimation accuracy of Algorithm2 and Algorithm3 is higher than that of Algorithm1, indicating that Algorithm2 and Algorithm3 can deal with the problem of multiplicative noise. It can be concluded from Figs. 4(c)-(d) that when the multiplicative measurement noise is not correlated with the additive measurement noise,and Algorithm2 and Algorithm3 have the same estimation accuracy.

6.4. Performance comparison of Algorithm2 and Algorithm3

Considering that the multiplicative measurement noise is correlated to the additive coutnerpart, in order to verify the estimation effect of Algorithm3 proposed in this paper, and Algorithm2 and Algorithm3 are compared. The simulation results are shown in Fig. 5. Obviously, Algorithm3 has a higher estimation accuracy than Algorithm2. The CKF algorithm with correlated multiplicative noise proposed in this paper can effectively deal with the problem of correlated noise.

6.5. Simulation result of Algorithm4

In order to verify the effectiveness of the adaptive CKF algorithm with correlated multiplicative noise proposed in this paper, the inaccurate noise correlation coefficient will be used for simulation verification in this case. The simulation results are shown in Figs. 6-9.

In this case,we set d used in the filter to 0.05,while d in the actual system is 0.045,and the simulation results are shown in Fig. 6 and Fig. 7. As can be seen from Fig. 6, the estimation error of Algorithm4 is smaller than the estimation error of Algorithm3. It can be seen from Fig. 7 that the estimation of d under Algorithm4 is close to the true value. When d in the actual system is 0.5, the value used in the filter is kept unchanged at 0.05, and the simulation results are shown in

Fig. 8 and Fig. 9.Obviously, in this case, the estimation accuracy of Algorithm3 is seriously reduced and it is close to divergence, while Algorithm4 still maintains a high estimation accuracy, and the estimated value of d is closer to the true value.

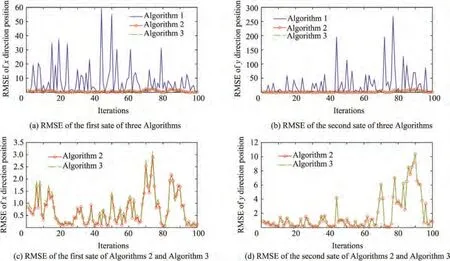
Fig. 4 Performance comparison of three algorithms.

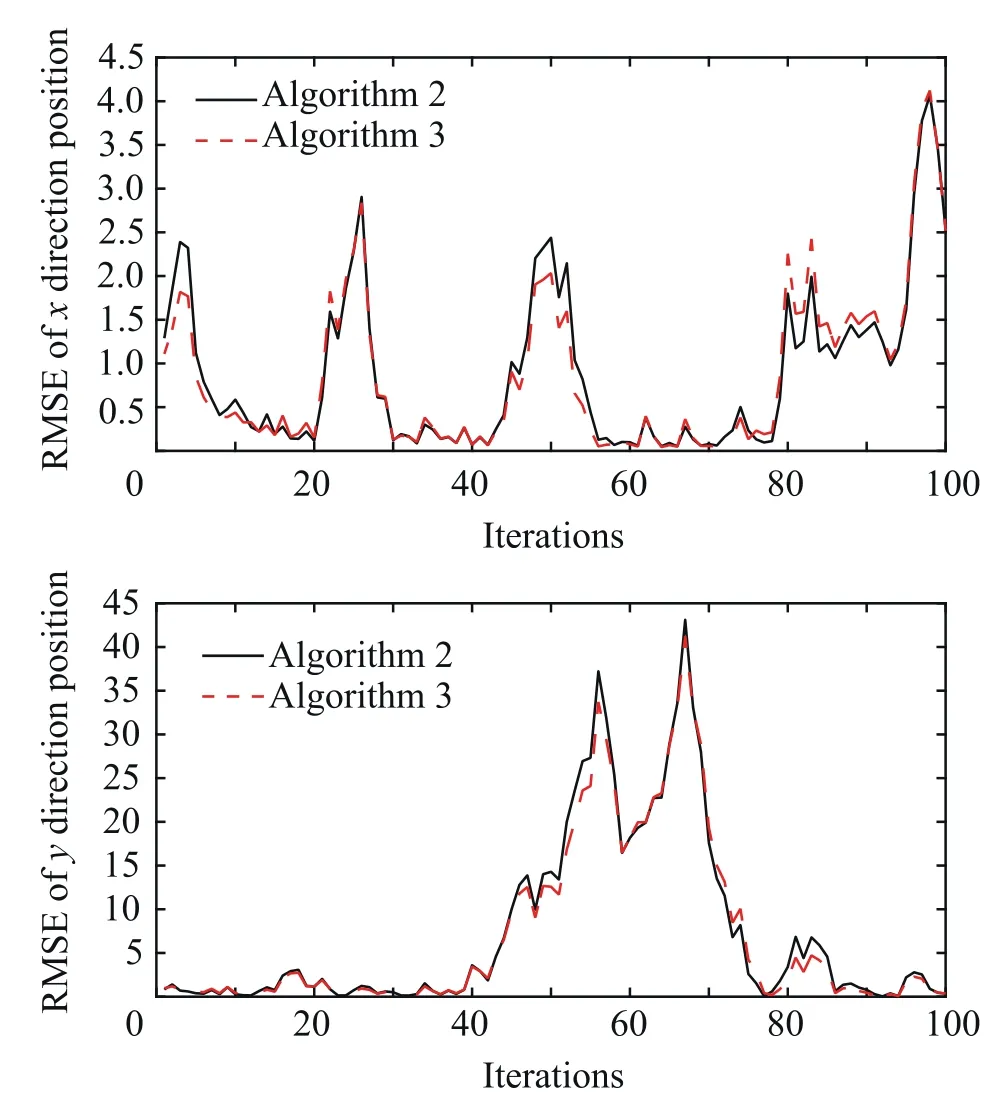
Fig.5 Performance comparison of Algorithm2 and Algorithm3.

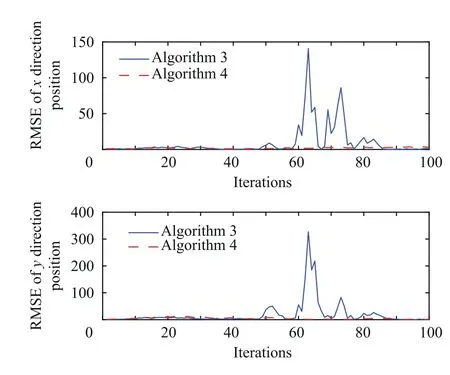
Fig. 6 Performance comparison when actual dk = 0.045.

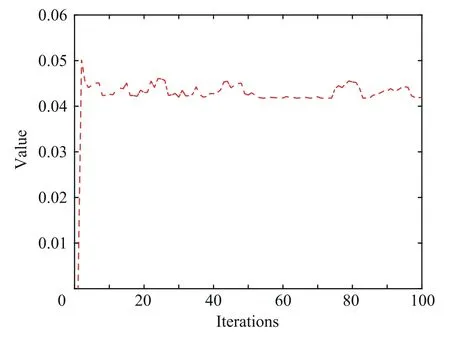
Fig. 7 Estimated value of dk =0.045.

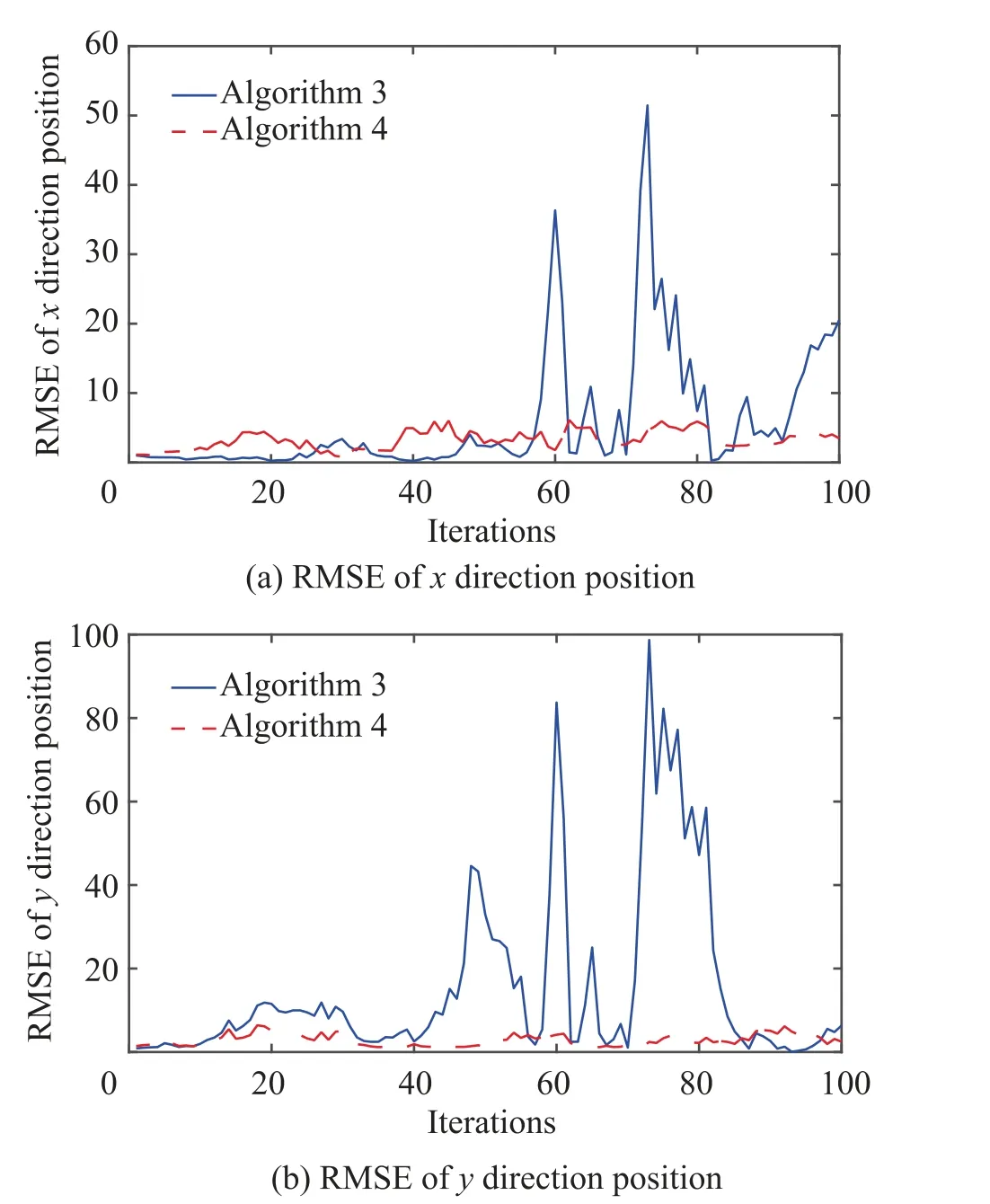
Fig. 8 Performance comparison when actual dk = 0.5.

6.6. Brief discussion

The trace of the measurement expected value E｛h（x）｝1is shown in Fig.10.Obviously,the value is witnessed a increasing trend at first, and finally tends to be gentle and greater than zero. For the four algorithms, the average running time is shown in Table 2. The simulation results taken from the computer with CPU 2.20 GHz and 8 GB internal storage show that,for the three algorithms with multiplicative measurement noise, the time costs are more than the CKF without the multiplicative noise. It is certain to spend additional computational burden. For the running time, Algorithm2 is less than Algorithms 3 and 4 because Algorithms 3 and 4 need to deal with the correlation of multiplicative measurement noise.Moreover, Algorithm4 needs to estimate the correlation coefficient on the multiplicative measurement noise, so it needs more running time.However,for the modern increasing ability on CPU and internal storage, the time spending is very small.Thereby,the computational complexity is comletely acceptable for the proposed adaptive CKF algorithm.

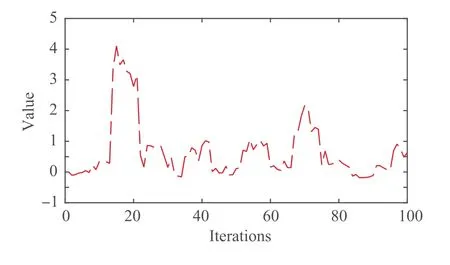
Fig. 9 Estimated value of dk = 0.5.

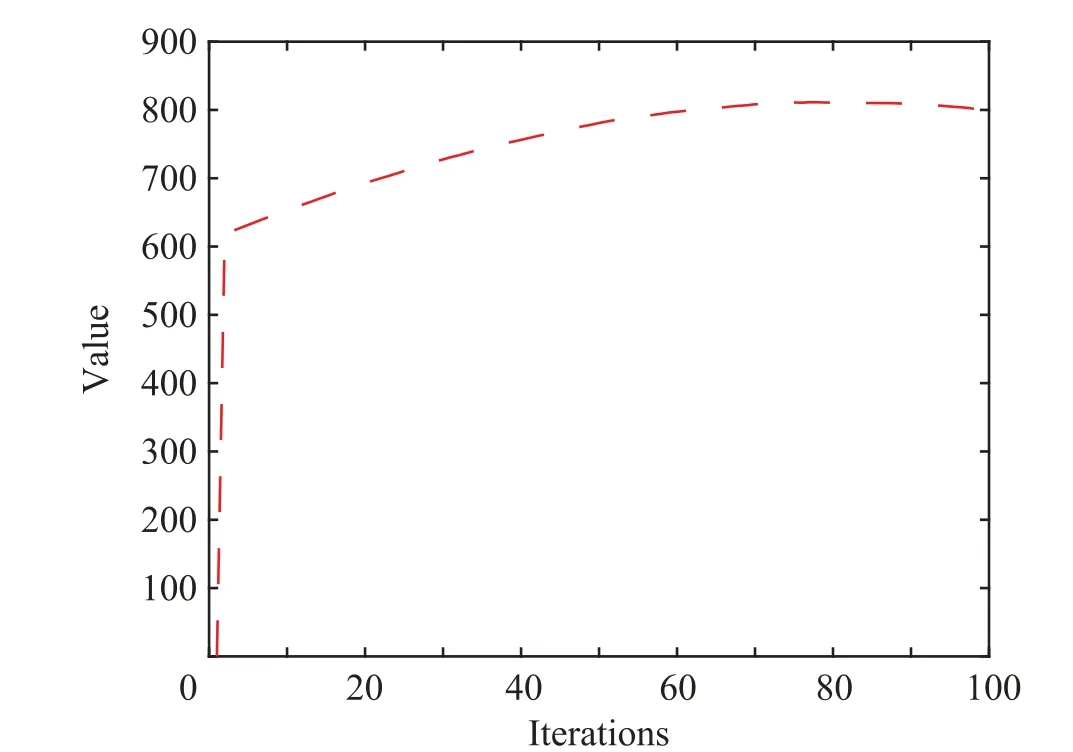
Fig. 10 Expected value of measurement.

Table 2 Comparison of time spending for four algorithms.

7. Conclusions

This paper investigates state estimation issues in mobile robot tracking,where multiplicative measurement noise is correlated with the additive one. A correlation multiplicative measurement noise model is firstly established, and the estimated performance mismatch problem of traditional CKF is analyzed.Based on the Gaussian filter framework, a modified filter capable of processing the correlated multiplicative noise is designed, and the CKF algorithm with correlated multiplicative noise is then obtained.Considering the inaccurate filtering problem of model parameters, a weighted fusion innovation covariance estimation method is proposed to estimate the correlation of noise.Thus,an adaptive CKF with correlated multiplicative noise is accomplished.The corresponding algorithm performance is also discussed. In the future work, some other adaptive estimation ways, including innovation theory,variational Bayesian theory, and machine learning, should be used to design the dynamical estimation scheme of the correlation coefficient for the multiplicative noise system.Meanwhile,the design of interactive multiple model algorithm is also one of interesting works based on the proposed filter.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China(Nos.61773147 and 62033010),Zhejiang Provincial Nature Science Foundation of China (Nos.LR17F030005 and LZ21F030004), and Key- Area Research and Development Program of Guangdong Province, china(No. 2018B010107002).