Distributed state estimation for linear timeinvariant dynamical systems: A review of theories and algorithms

Shuiting HUANG, Yuzhe LI, Junfeng WU,*

a College of Control Science and Engineering, Zhejiang University, Hangzhou 310027, China

b State Key Laboratory of Synthetical Automation for Process Industries, Northeastern University, Shenyang 110004, China

KEYWORDS Dynamical systems;Distributed estimation;Kalman filter;Luenberger observer;Linear systems;Multi agent systems;State estimation

Abstract Distributed state estimation is of paramount importance in many applications involving the large-scale complex systems over spatially deployed networked sensors.This paper provides an overview for analysis of distributed state estimation algorithms for linear time invariant systems.A number of previous works are reviewed and a clear classification of the main approaches in this field are presented,i.e.,Kalman-filter-type methods and Luenberger-observer-type methods.The design and the stability analysis of these methods are discussed.Moreover,a comprehensive comparison of the existing results is provided in terms of some standard metrics including the graph connectivity,system observability, optimality, time scale and so on. Finally, several important and challenging future research directions are discussed.

1. Introduction

State estimation plays a pivotal role in the entire field of control and some other fields.It has a well-established theory such as Kalman Filter(KF)and Luenberger Observer(LO).A huge body of research involves the design of state estimators operated in a centralized fashion, called centralized state estimation, that is, an estimator as a center collects and fuses all sensor data to compute system states, see Fig. 1 for illustration.In modern Cyber-Physical Systems(CPSs)or Networked Control Systems (NCSs) such as power grids, transportation systems and so on, the dynamical states, which are usually in large scale and complex, need to be monitored by a large collocation of sensors. It is exposed to many shortcomings for a centralized state estimation scheme, including high communication burden, huge computation, and poor robustness. In response to the recent increasing demand, distributed state estimation has attracted considerable attention.

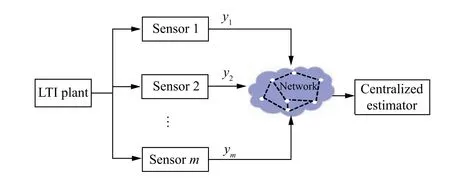
Fig. 1 Diagram of centralized state estimation.

In distributed state estimation, each subsystem (sensor or agent)is required to recover the entire state of the system using the local measurement and local communication with its neighboring subsystems. The distributed state estimation can be applied to various practical engineering tasks with massive sensor deployment and scarce communications, including aeronautics and astronautics,localization,environmental monitoring,security and surveillance,power grid operation,traffic managementand many others.We take the field of aeronautics and astronautics as an example. There are many results related to the distributed state estimation in this field, such as aerial target tracking in Refs. [18,19], cooperative control based on distributed observer for aircraft/spacecraft swarm in Refs.[20,21]and aero-engine state estimation for a distributed sensor network in Ref.[22].A diagram of typical distributed estimation is given in Fig. 2. Basically it consists of a group of local estimators that respectively sit in different subsystems and exchange information via a communication network. The major challenges of them is to develop communication and computing algorithms so that each of them can obtain the global state estimates from local information exchanges.In this paper,we focus on providing an up-todate overview of recent developments of distributed state estimation.They will be categorized and introduced from a unified perspective to ease reading.

In recent decades, there have been many surveys sketching the related fields about distributed estimation, such as Refs.[23-33]. The methods developed along the research line of information fusion, mainly surveyed in Refs. 23,24,27], have played an important role in the early development of distributed estimation theory.The workfocus on fusion algorithms applied in object tracking. Recent algorithms of distributed estimation are mostly consensus-based ones, with more details can be seen in Ref. [28]. The surveysalso provide an overview of such kinds of methods. In particular,in the big pool of the research related to distributed estimation,Distributed Kalman Filtering (DKF) has drawn a significant amount of attention because Kalman filtering, as the optimal linear Minimum Mean-Squared Error (MMSE) estimator for dynamical systems in the presence of system and measurement noises (Moreover the Kalman filter is the globally optimal MMSE estimator for Linear Time Invariant (LTI) dynamical systems when these noises are assumed to be Gaussian.), has numerous applications in technology,signal processing,econometrics and so on,reviewed in Ref.[30].In addition,results on distributed observers for Discrete-Time (DT) LTI systems have been reported in the literature, see the latest survey.In summary, most of the reviews on the related works mainly concern the distributed estimation algorithms for a specific type of systems, such as discrete-time LTI systems,or part of the distributed estimation methods, such as the DKF,consensus-based methods.

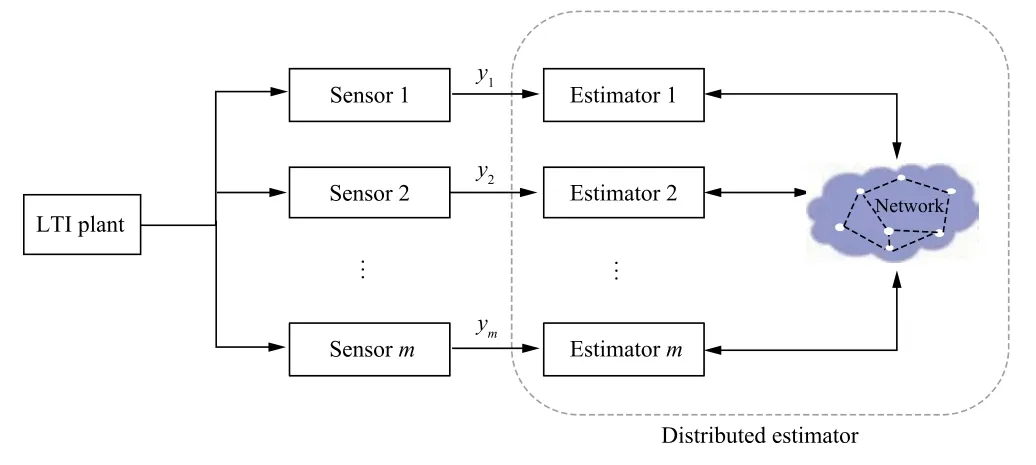
Fig. 2 Diagram of distributed state estimation.

In contrast with the above works,we will present a comprehensive overview of the main results on distributed state estimation for LTI systems (including discrete-time and Continuous-Time (CT) LTI systems) under a unified framework. We will summarize and give a clear classification of the main approaches in the related fields,to make it convenient for the readers to understand the most important underlying principles systematically. The terms decentralized and distributed are notoriously confusing in the literature when we are talking about multi-agent arrangement architectures. In this paper, we focus on the results on distributed estimation where the sensor nodes are organized in a network of the form in Fig. 3.

The remainder of this paper is organized as follows.In Section 2, we briefly present preliminaries of graph theory, Kalman filtering, Luenberger observer and distributed consensus algorithm.They serve as basics of developing distributed state estimation algorithms. We also formally define the distributed state estimation problem in this part. In Sections 3 and 4, we introduce and discuss the main distributed estimation methods and algorithms in the existing works in detail. In particular,they are categorized by us into two classes, called Kalmanfilter-type methods and Luenberger-observer-type methods.The classification of the distributed estimation algorithms in this literature is given in Fig. 4 which presents the relations among the different methods and the development of the related research simultaneously. In Section 5, we discuss the results of the distributed state estimation in some interesting scenarios. Finally we end the paper by giving concluding remarks and discussing future in Section 6.

Terminology. Throughout the rest of this paper, the terms‘‘nodes”, ‘‘agents” and ‘‘sensors” are used interchangeably,as are the terms ‘‘communication network” and ‘‘graph”.

2. Preliminaries and problem formulation

This section will simply review basic knowledge of graph theory,Kalman filtering,Luenberger observer and the distributed consensus algorithm.

2.1. Graph theory

Fig. 3 Distributed computing structure in this paper.

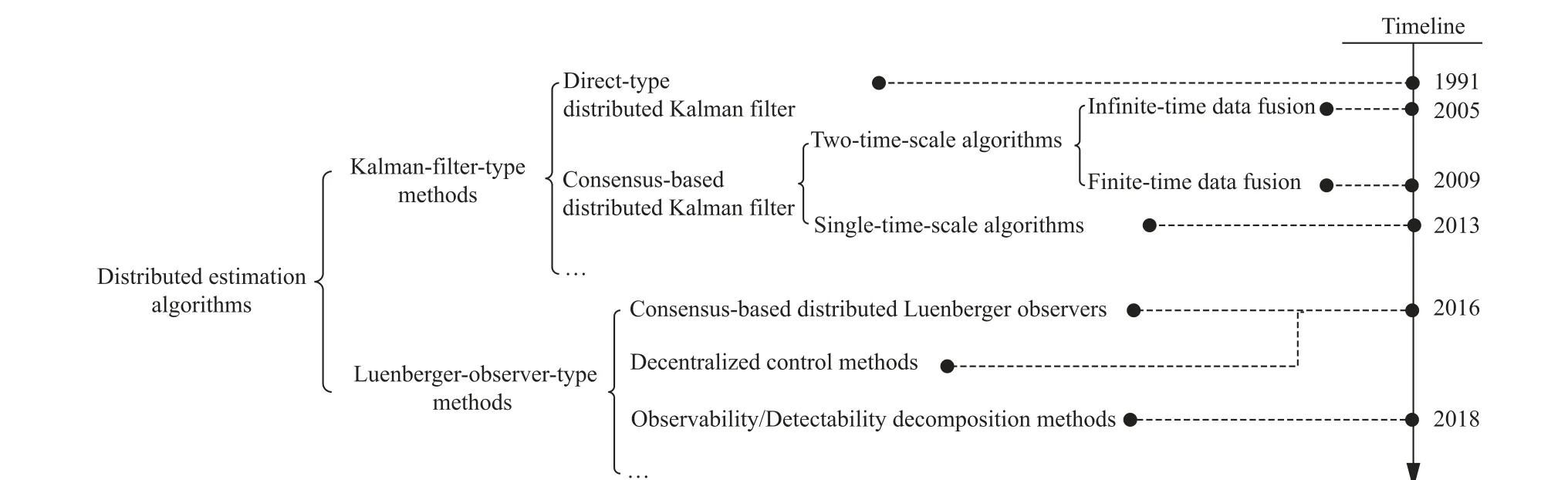
Fig. 4 Classification of distributed estimation algorithms in the literature.

2.2. Kalman filtering

We first introduce the Kalman filter in the context of a discrete-time LTI system.Consider a discrete-time LTI system with noise

Fig. 5 Graph G for Example 1.

Before presenting the convergence of the estimate produced by Eq. (2) (or Eq. (5)), we need an assumption:

Assumption 1. The system （A，C） in Eq. (1) (or Eq. (4)) is observable.

When the Assumption 1 holds,the estimation error asymptotically converges to a steady state. More importantly, the Kalman filter is an optimal state estimator which can minimize the mean square error between the estimate and the real state.

2.3. Luenberger observer

2.4. Distributed consensus algorithm

The distributed consensus problems can be formulated as agreement problems on linear combinations of reference signals or local parameters in a decentralized fashion over a network. More specifically, consider a network G= （V，E） and each agent i ∈V is assumed to hold a local reference signal s.The reference is distributed across the network,and it motivates the interest in developing distributed solutions for the consensus problem so that each agent i is able to reach an agreement regarding all local reference signals,namely the collective decision of the group of agents. To obtain the group decision, for agent i its local state can be updated in continuous time following a first-order dynamics

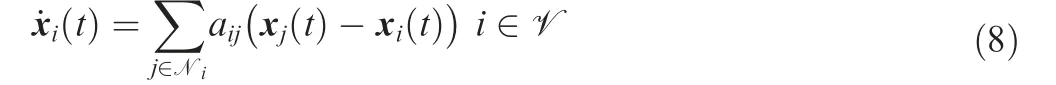
with x（0 ）=sand ais the entry of the adjacency matrix A.The dynamics of the entire network can be given in a compact form as:

2.5. Distributed state estimation for linear time-invariant dynamical systems

This section introduces the formulations of the distributed state estimation problem in a discrete-time system and in a continuous-time system, respectively.

Consider an LTI system

Definition 2 (Distributed estimator). Consider a system (12)monitored by N sensors in network G, a set of state estimate update and information exchange rules is called a distributed estimator if

Definition 3. MMSE distributed estimator. Consider a system(12) with uncorrelated Gaussian system noises, monitored by N sensors organized by a network G. A set of state estimate update and information exchange rules is called an MMSE optimal distributed estimator if its estimation error covariance is minimized.

Then,the distributed state estimation problem is defined as.

Problem 1. For an LTI system (12) monitored by the sensors,with the measurement models(13),organized by a network G,design a distributed estimator that is implemented at the individual side locally.

Remark 2. Since bounded noise has no impact on the stability of the state estimator, the solution of the distributed estimation problem for a noise-free LTI system also applies to that for an LTI system with bounded noise.

In a word, the distributed estimators that we are interested in this paper are limited to local measurements and communications. In what follows, we will provide an overview of some existing distributed state estimation algorithms for solving the distributed state estimation problem. Since there are different assumptions involving various system and network settings in the papers, different approaches have been developed. Our main concerns are the estimation update schemes and the stability analysis of estimation error dynamics for these approaches.

3. Distributed Kalman filtering

（），i ∈V. There have been many research works that concern about the design of the optimal MMSE estimators in this setting. Following the line of research on the standard Kalman filter, these works developed estimation algorithms for the satisfaction of covariance minimization in a distributed fashion,called Kalman-filter-type methods in this paper.

In the following,we review the Kalman-filter-type methods in chronological order. At the early stage some researchers generalized the centralized Kalman filter to sensor network under the assumption of local observability,which can be treated as a direct extension of the standard Kalman filter.It is termed direct-type distributed Kalman filter in this paper.Since the 2000s, a class of methods, termed consensus-based distributed Kalman filter,has dealt with the distributed estimation problem under a joint observability assumption,a weaker assumption than the local observability, see Remark 1 and Example 2 for discussion in details.The consensus-based distributed Kalman filters feature consensus iterations implemented at each agent to agree on some global information.In this sense,the stabilization of the Kalman filter under joint observability becomes possible, while on the other hand we need to assume the network to be organized with connectivity (to be precise, connectivity is necessary for an undirected graph and strong connectivity for a directed graph)for the agreement. Next we present the main idea and representative works of the direct-type distributed Kalman filters in Section 3.1 and then introduce the consensus-based distributed Kalman filter in Section 3.2.

3.1. Direct-type distributed Kalman filter

3.2. Consensus-based distributed Kalman filter

This subsection presents distributed estimation algorithms that introduce the consensus scheme into Kalman filtering iterations.The existing consensus-based distributed filtering results can be categorized into two classes in terms of the time scales in implementation, i.e., the two-time-scale algorithms and the single-time-scale algorithms.

We start by reviewing the two-time-scale distributed filtering for discrete-time systems, proposed in works such as Refs.[47-50,36,51,44,52]. Some distributed estimation algorithms applied in the field of aeronautics and astronautics can be classified into this category, such as the results in Ref. [18]. These algorithms are related to the information form of the Kalman filter (3), by which the distributed estimation problem can be reduced to two separate problems as follows: (A) state prediction and correction problem, where each node performs the information filter iterations to obtain the state estimates; (B)consensus problem, which dynamically tracks the average of the information matrices for each node to do correction update. The idea of the consensus-based distributed Kalman filter was first proposed in Ref. [47], which only presents an approximate distributed Kalman filter based on average consensus in full-information case, but does not clarify it further.The authors of Ref. [48] formally illustrated how to combine the consensus algorithm with the distributed Kalman filtering to solve the distributed estimation problem, and provided the analysis in detail.

In the algorithm proposed in Ref.[48],the consensus-based distributed Kalman filter comprises of two parts:consensus filters and micro-Kalman filters, The architecture of which is depicted in Fig. 6. In particular, the prediction equations of micro Kalman filter at the ith node are same as Eq.(14)while the correction equations are updated as follows:

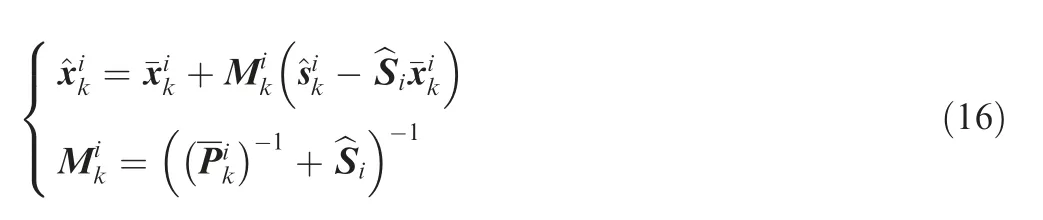
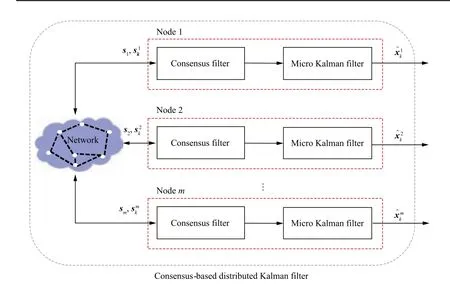
Fig. 6 Diagram for the consensus-based distributed Kalman filter in Ref. [48].

Each node needs to send its measurements,including sensor data and covariance data,to others in the network to agree on two central sums. The authors of Ref. [48] gave the following stability results:

Theorem 1 Theorem 1 of Ref.[48]. Consider a connected graph G. Assume the nodes solve two consensus problems that allow them to calculate average inverse-covariance Sand average measurements sk at every iteration k. Then, every node of the network can calculate the state estimate ^xat iteration k using the update equations of its micro Kalman filter.

Theorem 1 implies that this network of micro Kalman filters can provide the same estimate of the system state as a central Kalman filter provided that a sufficiently large number of consensus iteration step per sampling interval is performed,best of all, l→∞, which is an ideal situation. In another paperof the same authors,this kind of distributed estimator is further discussed, where the optimal gain matrix of this distributed Kalman filter is derived and the formal stability and performance analysis is provided by Lyapunov theory. It provides a bounded estimation error covariance only if the local observability for each node i holds, which becomes true only a sufficiently more considerable number of consensus iteration step l. Various distributed Kalman filtering algorithms with finite consensus step iterations have been researched in the literature,which is an improvement over the infinite data fusion case.

It should be pointed that this type of consensus-based distributed Kalman filter is a two-time-scale algorithm, which means that they require a number (theoretically, an infinite number) of consensus iterations for reaching an agreement between two consecutive time steps k and k+1 of estimate update; in other words, the outer ring is the state update and the inner ring is the data fusion by averaging consensus, see Fig. 7 for details. Moreover, the measurement sensing and state update occur at a slow time scale. The fast time scale is the data fusion time scale by consensus algorithm with a faster communication rate between neighbors. Two-time-scale algorithms have certain limitation in the case that the plant dynamics is also at a fast time scale.

Next, we review another consensus-based distributed filtering algorithm where data fusion and estimate update are performed simultaneously, called single-time-scale algorithms.Inspired by the results of Refs.[54,55],a single-time-scale Distributed Information Kalman Filter (DIKF) was constructed to achieve asymptotically unbiased estimates with bounded mean-squared error for unstable systems in Refs. [56-58].The authors of Ref. [31] proposed a representative singletime-scale distributed filter called Hybrid Consensus on Measurements-Consensus on Information (HCMCI) algorithm which applied an earliest data fusion method, referred to as covariance intersection,to the distributed state estimation problem.In detail,the prediction equations of HCMCI algorithm are same as the standard Kalman filter, given by

■

From Eq. (18), we know that the update of estimate needs each agent to exchange the estimate data and covariance data,which implies the heavy computation and communication.Some results of the workare employed to prove the stability of the estimation error dynamics, and more details can be found in Refs. [31,64]. We summarize as follows:

Theorem 2 (Theorem 1 of Ref. [31]). Let A be invertible.Assume that the pair （A，C） is observable, i.e., the system is jointly observable. If the consensus matrix Pis row stochastic and primitive,which can be guaranteed by the condition that the network is strongly connected,the estimation error covariance at each node i remains bounded using the distributed consensusbased Kalman filter (17) and (18).

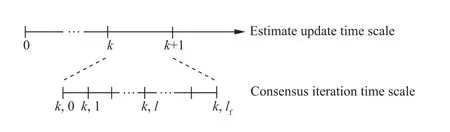
Fig. 7 Illustration of two-time-scale operation.

Although this method removes the strong assumption of local observability, it can not obtain the optimal estimate in the stochastic case. Other data fusion methods are applied in the distributed state estimation solution, including the largest ellipsoid methodand the covariance union method.In addition, the authors of Refs. [67,46,68-72] proposed another class of single-time-scale consensus-based distributed filtering approaches which combine the Linear Matrix Inequality(LMI) method to solve the distributed state estimation problem. The results of these approaches involve some LMIbased feasibility conditions, such as certain nonlinear matrix inequalities.

The works aforementioned discuss the construction of the consensus-based distributed Kalman filter for a discrete-time system.In the following context,we simply review some results of optimal consensus-based distributed filter of a continuoustime system (12b) and (13b). In Ref. [73], a continuous-time distributed Kalman filter was proposed as follows:

4. Distributed Luenberger observers

4.1. Consensus-based distributed Luenberger observers

Theorem 3 gives a sufficient condition on the number of consensus iterations leading to stable distributed estimation of the system(12a).A recent workcan be viewed as an extension of Ref.[78]by the same authors,where the outputs of distributed Luenberger observer are directly used to control the dynamical system and it demonstrates the effectiveness of this algorithm. Moreover, in the stochastic case, when l→∞,the covariance of estimation error of this distributed estimator converges to that of the centralized Kalman filter.Besides,this method is two-time-scale too.

A single-time-scale distributed Luenberger observer can be found in the work.We take the distributed estimator of Ref. [54] as an example to briefly introduce this kind of algorithm. The form of the distributed Luenberger observer proposed in Ref. [54] is given by

4.2. Decentralized control methods

In this subsection, we will review some distributed estimation works in the literature, where the classical decentralized control tools are utilized. The authors of Refs. [80-82] first transformed the problem of devising a stable distributed observer into that of constructing a decentralized controller in decentralized control systemsfor in the discrete-time LTI system. In the subsequent work,the authors generalized the result in the continuous-time setting. Before reviewing the two algorithms and their successors,we briefly introduce some classical results in decentralized control.

Consider a Multiple Input Multiple Output (MIMO) system denoted by

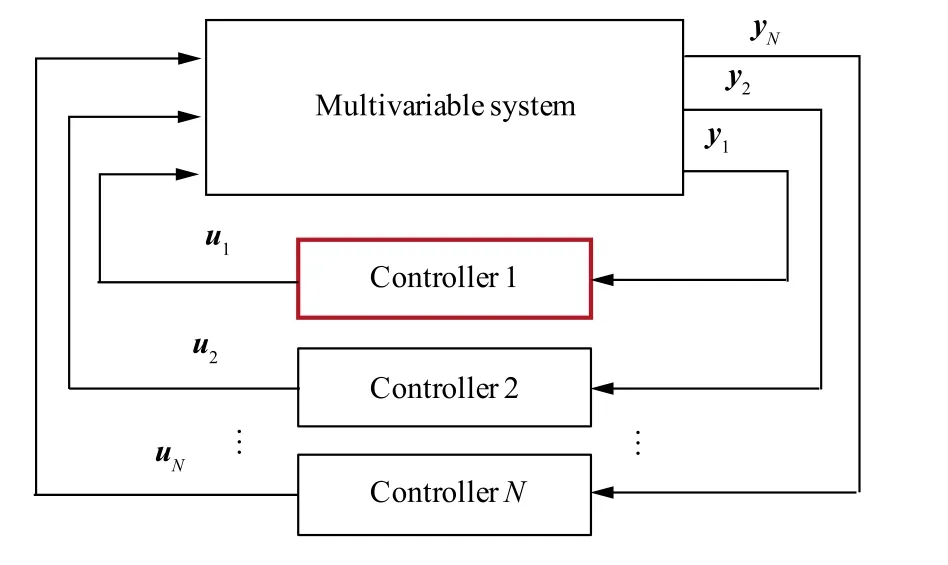
Fig. 8 A closed-loop MIMO system with a decentralized controller.

In Ref.[80],the authors derive a sufficient condition for the existence of the distributed observer. In another paperpublished in the same year, necessary and sufficient conditions are provided given a symmetric weight matrix P, i.e., the underlying network is undirectedly connected. An important work in this direction is Ref. [82], where the authors extend the results under a directed graph, i.e., the weight matrix Pis asymmetric.

Now,we illustrate how to transform the distributed estimation problem into a decentralized control problem. Consider the network is a strongly connected graph, the connection is established by estimation error dynamics represented as

It is pointed out in Ref. [82] that the average dimension of each observer’s state does not exceed n+1.To be more specific, in the distributed observer developed in Ref. [82], the dimension of only one of the local observers in each source component is n+ν-1, while other local observers’ dimension is equal to n.

The authors of Ref.[86]employed the decentralized control theory to solve the distributed estimation problem for continuous-time LTI systems,showing the possibility of freely assigning the convergence rate of the observer given that a pole placement technique using dynamic compensatorsis applied.The workput forward a general framework for the state estimators, which is

4.3. Observability/detectability decomposition methods

In this subsection, we review a class of distributed estimators design based on the observability/detectability decomposition.By resorting to the observability/ detectability decomposition methods, the state space of the system can be divided into two parts at each node: one part contains the system modes that are observable to the node, for which the state can be reconstructed by using its own measurements; the other part consists of the locally unobservable system modes, for which a stable estimation needs to exchange information with neighbors.

Two different observability/detectability decomposition methods are adopted in Refs.[88,89],resulting in two different distributed Luenberger observer design algorithms. The workfocuses on developing a stable distributed observer for a noise-free discrete-time LTI system.In this work N number of observable canonical decompositions,called a multisensor observable canonical decomposition, are performed, one for each sensor. The basic working principle underlying such a decomposition is as follows:first index the set of the sensors.Perform an observable canonical decomposition with respect to the first sensor. Then, perform an observable canonical decomposition with respect to sensor 2 within the unobservable subspace of sensor 1, and repeat the process until we are at the last sensor. This decomposition process in total can be identified as a similarity transformation, completed by a coordinate transformation x=Rzwith an invertible matrix R ∈R.The system(12a)and(13a)is transformed to

By Eq. (30) and Theorem 6, we are able to design a stable observer for the transformed system(29).Then using the relation x=Rz,we obtain the distributed observer of the system(12a). In contrast to the results in Ref. [86], the convergence rate of the observer(30)cannot be freely assigned and is influenced by the index of the nodes in the multisensor observable canonical decomposition as well as the topology of the network.More specifically,some information exchanged between nodes will not be used to update state estimation, which influences the convergence rate. The authors of Ref. [90] proposed a distributed estimation algorithm based on multi-hop subspace decomposition to address the shortage of freedom in convergence rate assignment for the method in Ref. [88]. In particular, the design method in Ref. [90] only requires a mild assumption on the network connectivity while have the ability to arbitrarily assign the convergence rate by combining the pole placement technique.

The matrix Lis chosen such that A-LCis Hurwitz,γand αare the coupling gain and consensus weight to be designed, respectively. Through the discussion of the stability of error dynamics ～x（t ）=x（t ）-^x（t ） and the construction of a Lyapunov function, the following theorem was established in Ref. [89] for the stability of the distributed observer (32).

Theorem 7 (Theorem 1 and 2 of Ref. [89]). Suppose that the communication network G is strongly connected and the pair（A，C） is detectable. Then the proposed distributed observer(32) has an error decay rate α>0 if Lis chosen so that the maximum among the real part of the eigenvalues of the matrix A-LCis less than -α for each node i ∈V, and γis chosen such that

In comparison to the design in Ref. [75], where each local observer shares the same coupling gain,in Ref.[89]each node i can choose its own gain to be different from others’ gains.Moreover, coupling gain can be arbitrarily chosen to satisfy Eq. (33) by itself. It is stressed that this algorithm does not need any global information, including the graph topology,the number of the nodes, the others’ observation matrices, so it is treated as a decentralized distributed observer design.Similar design approaches were adopted in Refs. [92,93]. Specifically, the authors of Ref. [92] constructed a distributed observer with the same structure and gave the stability analysis of the estimation error dynamics using the Linear Matrix Inequality (LMI) technique. The same authors proposed a minimal order distributed observer in Ref. [93]. The authors of Refs.[94-97]used the same structure to design a distributed observer and converted the distributed estimation problem into the optimization problems. In addition, as pointed out in Remark 3, the above mentioned distributed observers also work under the assumption that every source component of a network is detectable.

5. Extensions in other interesting scenarios

The discussions on the traditional state estimation (i.e., the Kalman filtering and Luenberger observer)in some interesting scenarios have always attracted researchers. There are many results, such as the worksrelated to the state estimation against malicious attacks, Refs. [102-104] discussing the state estimation under limited communication resource or quantized measurements. In this section, we briefly introduce the results of the distributed estimation problem subject to such realworld scenarios, including malicious attacks,network topology changes,and quantized communications.

The vulnerability and openness of communication links makes it possible for potential malicious attackers to threaten the estimator’s stability and performance.It is of paramount importance to design a resilient distributed estimator considering malicious attacks. Many researchers have focused on developing the security-aware distributed estimation schemes against the Byzantine adversarial behavior,where a compromised node by the Byzantine adversary possesses complete knowledge of the system and can deviate arbitrarily from the rule of any prescribed algorithm.The workcharacterizes fundamental limitations of any distributed state estimation algorithm in terms of the measurement model and the graph structure in the presence of nodes compromised by Byzantine adversaries, and designed a resilient distributed filtering algorithm for a general LTI system over a so-called strong-robustness network.The authors of Ref.[110]discussed the construction of a resilient distributed observer for mobile agents surveillance and patrolling applications against communication losses and intermittent observations. More recently,the distributed estimation problem under the sensor attacks was studied in Ref.[111],where the authors developed a secure distributed estimator by exploiting a saturation-like scheme and a consensus strategy to make the estimation error dynamics stable.A fast resilient distributed Kalman filter in the presence of attacks was proposed in Ref. [112], where the algorithm produces bounded state estimation errors despite the magnitude of the attack and the number of compromised sensors.

Time-varying communication networks are present in CPSs or NCSs due to the failure of the nodes,sleep mode of the sensors for energy saving,or wireless communication channel failures. The authors of Ref. [113] constructed a hybrid observer comprised of the continuous-time linear observer and the local parameter estimator under a time-varying directed graph that is strongly connected all the time to make each estimate converge to the state of the system with a freely assigned convergence rate. The finite-time distributed observer proposed in Ref. [114] addressed the distributed estimation problem under a time-varying directed communication graph by exploiting the age-of-information, a notion of a ‘‘freshness-index” of information.The workexploited the properties of invariant subspaces and properties of perturbed systems to construct a simply structured distributed observer for a continuous-time linear system over a time-varying network. Recently, the authors of Ref. [116] adopted the covariance intersection fusion technique to design a consensus-based distributed estimator for a linear time-varying system with random link failures.

From a practical perspective,the estimation performance is influenced by the fact that there are stringent communication limitations embodied in energy, channels and bandwidth in CPSs or NCSs. There are many works discussing the remote state estimation with the communication limitation, such as Refs.[117-120],where different transmit power control strategies are proposed to achieve better estimation performance.Similarly,the distributed estimation problem for a system with quantized and rate-limited communications has attracted many attentions.The authors of Refs.[78,79]combined a uniform quantizer with a consensus algorithm to develop a distributed Luenberger observer facing limited communication.The workdesigned a quantized gossip-based distributed Kalman filter for quantized communication links. Recently,the authors of Ref. [122] handled the distributed estimation problem for system uncertainty with switched network topology and quantized communication together by extending system state and introducing event-triggered scheme into the update of the distributed Kalman filter.

6. Summaries and concluding remarks

In this paper,we provide a review of existing discrete-time and continuous-time distributed state estimation algorithms for LTI systems. In particular, we describe the direct-type distributed Kalman filters in Section 3.1, discrete/continuous-time consensus-based distributed Kalman filters in Section 3.2,consensus-based distributed Luenberger observers in Section 4.1, discrete/continuous-time decentralized control methods in Section 4.2,and discrete/continuous-time observability/detectability decomposition methods in Section 4.3. Table 1 depicts the main characteristics of all the approaches reviewed in Sections 3 and 4.We compare the assumption of graph connectivity and observability, interactive information, time scale of the methods, and discuss the optimality of the distributed Kalman filters and the convergence rate of the distributed Luenberger observers.

In distributed state estimation problem, the assumption of graph connectivity and system observability can be categorized into four cases: a locally observable/detectable system over a connected undirected graph, a globally observable/detectable system over a connected undirected graph, a globally observable/detectable system over a strongly connected directed graph and a network where each source component is observable/detectable. The assumption becomes milder and milder.Specificially, the condition that each source component of a network is observable/detectable is a necessary and sufficient for the existence of distributed estimator, as shown in Ref.[82], which does not require the network to be strongly connected.

Information communication between neighboring nodes is a prominent feature of distributed estimation algorithms. In some algorithms, the transmitted data is real-time state estimates. The information matrices are exchanged in someconsensus-based distributed Kalman filtering algorithms.Besides,measurement exchanges are needed in some early proposed distributed estimation methods with the local observability requirement.

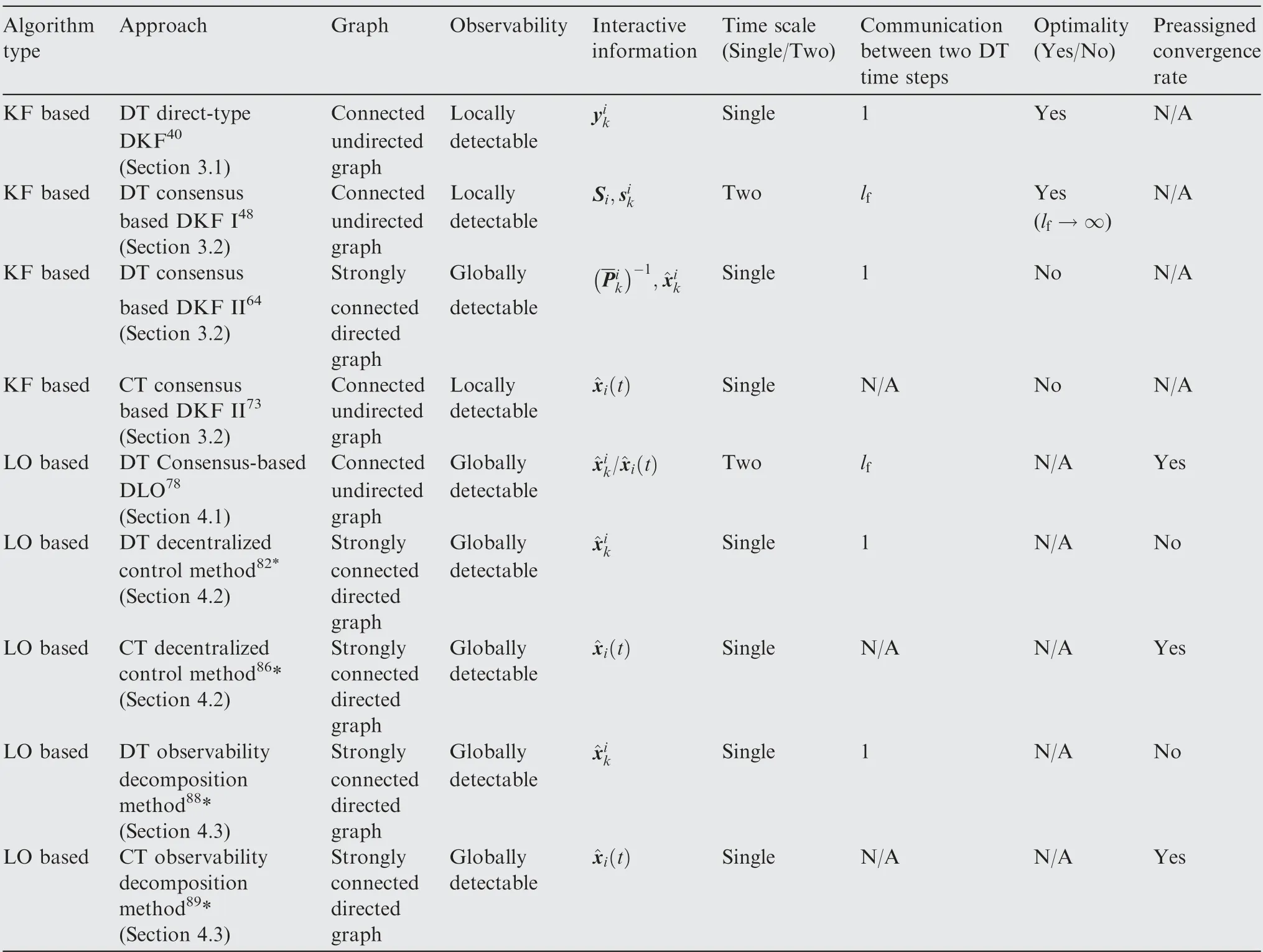
Table 1 Distributed state estimation algorithms for LTI systems.

In terms of communication rate, the communication between neighbors and the estimate update share the same rate in the majority of algorithms. However, a small part of consensus-based distributed estimation algorithms operates on two-time scale, where fast communication exchange between neighbors guarantees all nodes to achieve an agreement on some variables by a consensus strategy.

In what follows, we discuss the optimality of Kalmanfilter-type algorithms. Since the Kalman filter can get the optimal state estimate, we are concerned about the optimality of the distributed Kalman filters. Virtually, whether each node can obtain the covariance directly affects the optimality of distributed estimators. The two-time-scale consensusbased distributed Kalman filters can obtain the optimal estimate when l→∞ is satisfied. However, the single-timescale ones cannot because each node fails to obtain the covariance due to the unknown correlation between the nodes’ estimates. In addition, regarding the assignment of the convergence rate of distributed Luenberger observers,except for the early work,most work has considered this issue, which can be accomplished by exploiting the pole placement methods.

Finally,we provide several interesting future research directions, briefly summarized as follows:

1. Most distributed state estimation algorithms discussed in our paper are performed in a distributed fashion,but actually needs to be designed in a centralized fashion. Specifically, the design of a distributed estimator at each node cannot be carried out when some global information is absent from it, such as the number of nodes, other nodes’observation matrices, the topology of the entire network and so on. The whole algorithm’s parameters have to be updated as long as there is some certain change that happens at the network system level. The change could be increase/failure of communication links or node components, sleep of some nodes for energy saving, malicious attack behaviors, and mission requirements. Hence, it is an important research direction in the future to consider fully distributed design for a distributed estimator; that is,each node can by itself reconfigure the distributed estimation algorithm when it faces the aforementioned changes.

2. It is challenging for the development of resilient distributed state estimation algorithms when there are attack scenarios.Most of the existing results are investigations of distributed parameter estimation. With the presence of system dynamics, the state estimation for a dynamical system is more challenging than parameter estimation. Moreover, in the recent results the effectiveness of the secure distributed state estimation algorithms heavily relies on the connectivity of the graph and the number of nodes comprised by malicious adversaries. It is worthy of discussing the construction of resilient distributed state estimation algorithms under more relaxed assumptions.

3. In many distributed computing settings,each node has sensitive information about its own profiles. It is necessary to consider privacy issues. The workemployed the homomorphic encryption and proposed a state estimation paradigm that can preserve participants’ data and model privacy in multi-party state estimation case. This method is applied to the centralized state estimation as Fig. 1.How to develop privacy-preserving distributed state estimation approaches that can obtain the state estimate while protecting each node’s privacy needs further discussions.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

The work by S. Huang and J. Wu was supported by the National Natural Science Foundation of China (No.61790573). The work by Y. Li was supported by the National Natural Science Foundation of China (Nos. 61890924,61991404), and Liao Ning Revitalization Talents Program(No. XLYC1907087).