Variational Bayesian Kalman filter using natural gradient

Yumi HU, Xuzhi WANG, Quan PAN, Zhntao HU, Bill MORAN

a School of Automation, Northwestern Polytechnical University, Xi’an 710072, China

b The Key Laboratory of Information Fusion Technology, Ministry of Education, Xi’an 710072, China

c Department of Electrical and Electronic Engineering, The University of Melbourne, Melbourne, VIC 3010, Australia

d School of Engineering, RMIT University, Melbourne, VIC 3000, Australia

e School of Computer and Information Engineering, Henan University, Kaifeng 475001, China

KEYWORDS Kullback-Leibler divergence;Natural gradient;Nonlinear Kalman filter;Target tracking;Variational Bayesian optimization

Abstract We propose a technique based on the natural gradient method for variational lower bound maximization for a variational Bayesian Kalman filter. The natural gradient approach is applied to the Kullback-Leibler divergence between the parameterized variational distribution and the posterior density of interest.Using a Gaussian assumption for the parametrized variational distribution, we obtain a closed-form iterative procedure for the Kullback-Leibler divergence minimization, producing estimates of the variational hyper-parameters of state estimation and the associated error covariance. Simulation results in both a Doppler radar tracking scenario and a bearing-only tracking scenario are presented, showing that the proposed natural gradient method outperforms existing methods which are based on other linearization techniques in terms of tracking accuracy.

1. Introduction

Nonlinear estimation problems occur across a multitude of applications, including aerial surveillance, target tracking,and intelligent vehicles.Typically, the optimal estimator is not available for these problems because the posterior Probability Density Function(PDF)of the random variable of interest (the state) is mathematically intractable. In consequence,suboptimal methods are sought to provide approximations for the nonlinear state PDF. Suboptimal filters such as the Extended Kalman Filter (EKF),Iterative Extended Kalman Filter (IEKF),the Unscented Kalman Filter (UKF),and the Cubature Kalman Filter (CKF),as well as Sequential Monte Carlo (SMC)methods and their variants have been derived to provide approximate solutions to the nonlinear estimation problems. Overviews of a series of suboptimal nonlinear filters are available in Refs. 8-10.

Classical optimization techniques, such as gradient-based methods, may be used in the linearization for these nonlinear problems and solve the problems numerically by parameterized iteration. In this class, the natural gradient method described in Ref. 11 computes the gradient step size and descent direction on a statistical manifold that spanned by the Fisher information matrix in question.We adopt Amari’s natural gradient approachto solve the nonlinear variational parameterization against the Kullback-Leibler Divergence(KLD) between the approximating parametric distribution and the PDF. As shown in Ref. 12, the natural gradient method for nonlinear estimation problem is proved to be asymptotically optimal in the sense of Carme´r-Rao bound.

The use of natural gradient is proposed as a Kalman filterlike method for joint estimation of state and parameters,where(batch) non-real-time data are collected to estimate parameters.Natural gradient is also used in Ref. 14 for sensor network target tracking. There the measure of closeness is the geodesic distance in the Fisher-Rao metric. In effect, the approximating distribution moves from the current location to a new one along the geodesic in the direction of the natural gradient.

Recently,the Variational Bayes(VB)method has become popular for approximation of the posterior density by a tractable variational distribution, converting the problem of calculating a nonlinear PDF integral to the optimization of Evidence Lower Bound (ELBO). Our recent work,a survey on variational Bayesian joint optimization is presented, which provided a unified framework to handle the problems of parameters identification and state estimation in multi-path multi-mode multi-target tracking system. In Ref. 17, a noisy natural gradient approach is used to find the steepest ascent direction of the objective function to maximize ELBO. In Ref. 17, the KLD is approximated by a differential term involving the Fisher information matrix,resulting in a genuine metric in a local neighborhood. However, the method only considers a static system model with application to Bayesian neural nets and logistic regression.

In our recent work,a regularization constructed by the weighted KLD between the variational distribution and the posterior PDF is considered to form a proximal nonlinear filter,resulting in a‘‘tight”approximation of the posterior PDF.We note an issue with the KLD: it fails to have the usual and natural properties of a distance (metric), namely, symmetry and the triangle inequality.

We propose a variational Bayesian Kalman filter where the natural gradient method is used for variational lower bound maximization against the Fisher information criterion.The latter is derived from the minimization of the KLD between the approximating distribution and the prior distribution. Under Gaussian assumption, the estimated state and the associated error covariance of interest are derived in closed-forms. The work presented here differs from our previous workin two points: (A) Objective functions are different. In Ref. 18, the objective function is the sum of ELBO and the negative weighted KLD between a variational distribution and the posterior distribution,with the weighted KLD acting as a regularization. In this paper, only ELBO is taken as the objective function,and it is split into two terms,namely,the expectation of log-likelihood and the KLD between variational distribution and the prior distribution. (B) Optimization methods are different.In Ref.18,the objective function(includes ELBO and KLD) is linearized by a Taylor expansion. A key feature of this paper is that the natural gradient is adopted in addition to the linearization. Our simulations show the proposed algorithm outperforms other methods of EKF,UKF,and IEKF in accuracy performance, and also verify that more iterations of the natural gradient algorithm result in a smaller KLD and thereby better approximations.

First of all,we introduce the general nonlinear Bayesian filtering problem. Then background on VB is provided. Finally,we propose the variational Bayesian Kalman filter using natural gradient and give two examples to verify the proposed method compared with EKF, UKF, IEKF and Proximal EKF (PEKF), and analyze the ELBO and KLD with varying numbers of iterations.

2. Problem formulation

We consider a general nonlinear discrete dynamical system with nonlinear measurements as

3. Variational Bayesian inference

4. Variational Bayesian Kalman filter using natural gradient

4.1. Variational Bayesian Kalman filter formulation using natural gradient

4.2. Implementation of variational Bayesian Kalman filter using natural gradient

Algorithm 1. VBKF-NG algorithm 1:Initialization:State estimation x0|0,estimation error covariance P0|0, the number of scan K, and iteration Iiter.2: for each iteration k = 1:K do 3: Compute the predicted state and the associated error covariance xk|k-1=fk|k-1 xk-1|k-1（）, Pk|k-1=Fk|k-1Pk-1|k-1FT k|k-1+Qk-1，where Fk|k-1=∂fk|k-1 （x ）∂x■■■x=xk|k-1.4: Iteration initialization: x1k|k =xk|k-1 and P1 k|k =Pk|k-1 .5: for each iteration i = 1:Iiter and e > ε do 6: Compute iterative state estimation xi+1k|k and its error covariance Pi+1 k|k by Eqs. (26) and (27), respectively.7: Compute relevant error e by Eq. (28).8: end for 9: Output xk|k =xik|k and Pk|k =Pi k|k .10: end for

4.3. Variational evidence lower bound of VBKF-NG

ELBO is monotonically increasing in the iteration index, so it is used to measure the convergence of the variational iteration.According to the derivational results Eqs. (26) and (27) in Section 4.2 and Eq. (5), we can rewrite the ELBO as

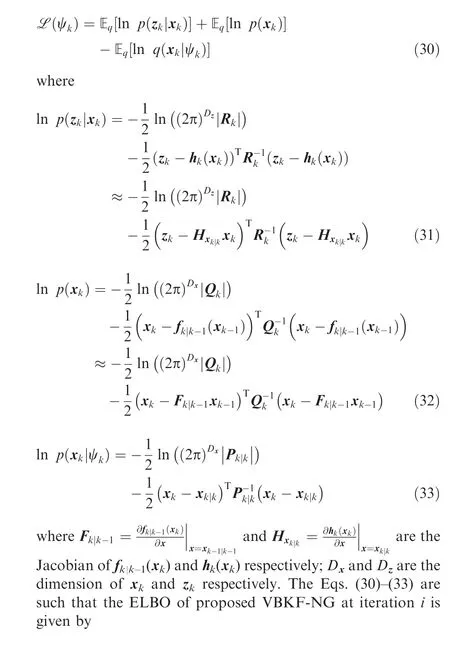
Fig. 1 Target tracking scenario with three Doppler radars.

The proof can be found in Appendix B in Ref. 18.

5. Numerical simulation

5.1. Target tracking using three Doppler radars

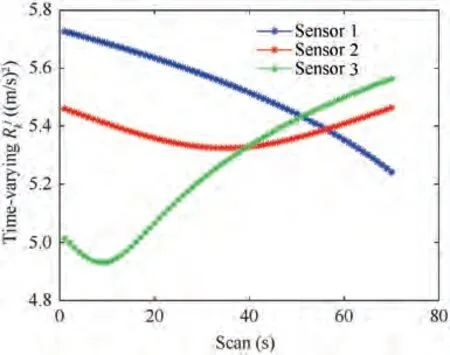
Fig. 2 Time-varying measurement covariance of sensors.

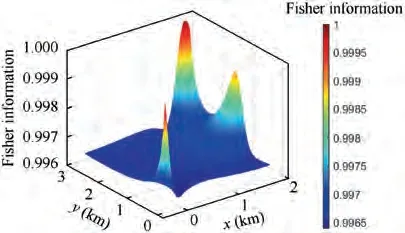
Fig. 3 Determinant of Fisher information provided by three sensors (at randomly selected Scan 47).

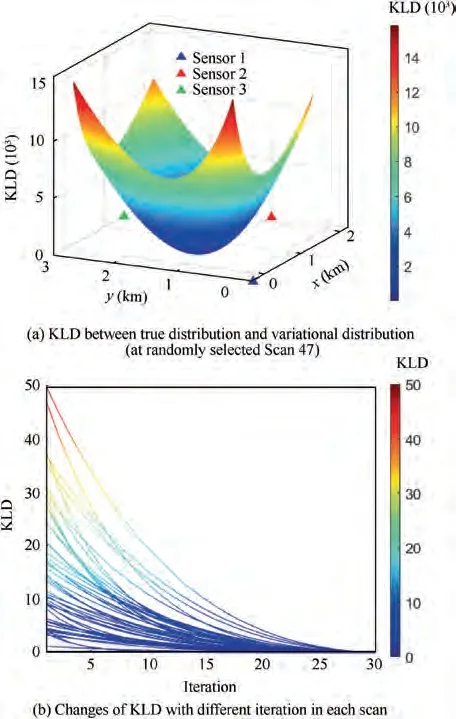
Fig. 4 KLD between true distribution and variational distribution and changes with different iteration in each scan.

Fig.4(a)is a mesh plot of the KLD value against the target location at a particular scan (Scan 47). It may be treated as a tracking accuracy map for a given Doppler radar network.For a further illustration,Fig.4(b)gives the KLD lines of all scans,each line indicates the changes of KLD with different iterations in one scan.

As we discussed in Section 3, minimization of the KLD is equivalent to the maximization of ELBO. To illustrate the ELBO changes over different iterations in VBKF-NG,we plot the normalized ELBO of VBKF-NG against the number of iterations in Fig.5,where each line denotes the ELBO of all 30 iterations of one scan. The value of ELBO increases with the number of iterations,corresponding to a decrease in the KLD.

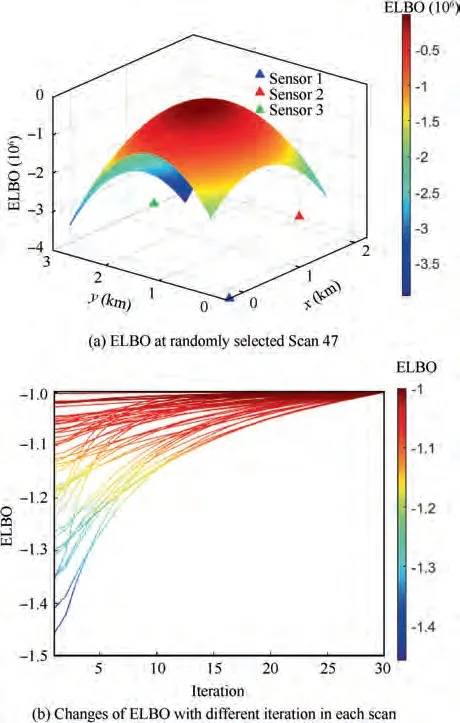
Fig. 5 ELBO at randomly selected scan 47 and changes with different iteration in each scan.

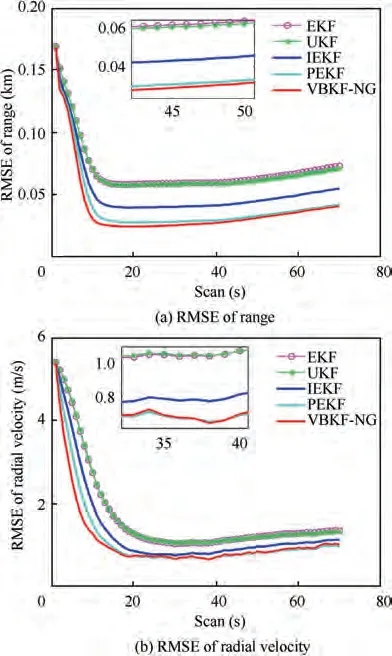
Fig.6 RMSE comparison in EKF,UKF,IEKF and VBKF-NG in scenario with three Doppler radars.

Fig. 6 shows the RMSE comparison of VBKF-NG, EKF,UKF, IEKF and PEKF, where Fig. 6(a) shows the RMSE of the range and Fig. 6(b) is the RMSE of the radial velocity.It is evident VBKF-NG outperforms the other methods in both cases. Effectively, the proposed VBKF-NG algorithm performs variational distribution optimization on the statistical manifold with Riemannian metric the Fisher information matrix.As a result,the iterative optimization of natural gradient method finds a better variational distribution that minimizes the KLD with the posterior.

The PEKF in Ref. 18 is an optimized filter that includes a regularization term, namely the weighted KLD. By the introduction of this weight, the PEKF is able to provide a balance between robustness and accuracy. The VBKF-NG algorithm proposed involves also an iterative optimization process, but this process moves in the direction of the natural gradient in a Riemannian sense.This is optimal from the information geometrical view point. Nevertheless, the error performances of the two are almost identical if the number of iterations is sufficiently large. As shown in Fig. 6, the RMSE performance of PEKF is slightly worse than that of VBKF-NG after 5 iterations.

For a further analysis,the mean computational cost of each scan from 1000 Monte Carlo is given in Table 1, from which we see that EKF has the smallest cost. All of IEKF, PEKF and VBKF-NG have higher computational costs than EKFand UKF;this is because of the need to calculate the Jacobian matrix in each iteration.We also see that the cost of PEKF and VBKF-NG is slightly higher than IEKF.

Table 1 Comparison of mean computational cost in scenario with three Doppler radars.

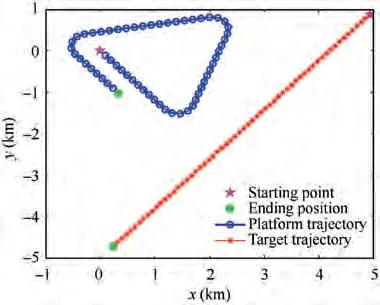
Fig. 7 Bearing-only scenario with a single sensor platform.

5.2. Bearing-only target tracking using a single sensor

A target is moving at a constant speed of 2.06 m/s with initial position[4924 m,868 m]and heading-140°as shown in Fig.7.The sensor platform is moving at a constant speed of 2.60 m/s and taking bearing measurements of the target at a sampling rate of 1/60 Hz. The platform starts from position [0 m,0 m]and makes turns along its way as shown in Fig. 7 to enhance observability of the target. Two maneuver models with their associated scan indexes are given:

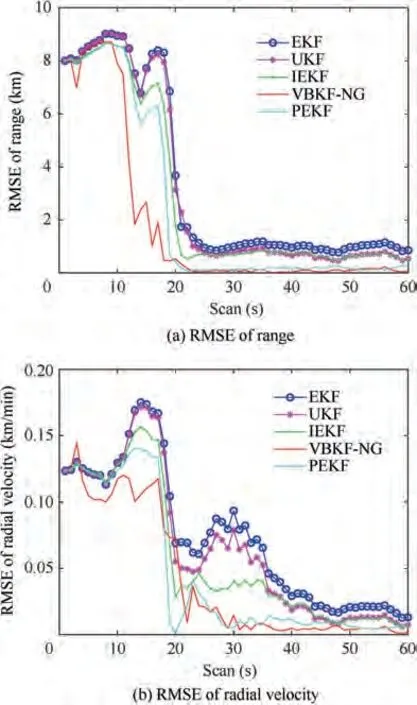
Fig.8 RMSE comparison in EKF,UKF,IEKF and VBKF-NG in bearing-only scenario.

Table 2 Comparison of mean computational cost in bearingonly scenario.

where[x,y]is the position of platform at Scan k;[x,y]is the position of the target. The sensor measurement error is assumed to be Gaussian distributed with zero-mean and standard deviation 3°. The system noise covariance Q=10Q,where

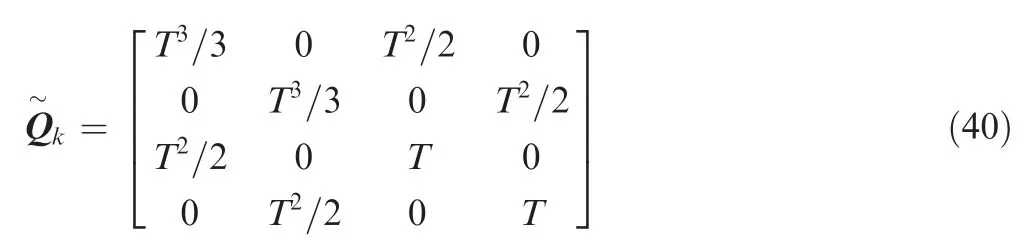
Simulation results are presented in RMSE of range and radial velocity of the target in Fig.8 averaged over 1000 Monte Carlo runs.As shown in Fig.8,the target becomes observable since the first maneuver of the platform has occurred during Scans 16-20 as indicated by the significant drop of RMSE curves.Among the five algorithms,the VBKF-NG has the best RMSE performance,and PEKF is slightly worse than VBKFNG. The comparison of mean computational cost between EKF,UKF,IEKF,PEKF and VBKF-NG is given in Table 2.Similar to Table 1,the VBKF-NG improves the accuracy performance at the expense of slightly higher computational cost than IEKF and very close to PEKF.

6. Conclusions

We proposed an iterative variational Bayesian Kalman filter in which a natural gradient approach is adopted for iterative ELBO maximization producing an appropriate variational distribution for the approximation of the state posterior PDF. Simulation results and analysis show that the proposed method outperforms EKF, UKF and IEKF filters that are used in the existing VB approaches.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This investigation was co-supported by the National Natural Science Foundation of China (Nos. 61790552 and 61976080)and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University, China (No.CX201915).

A