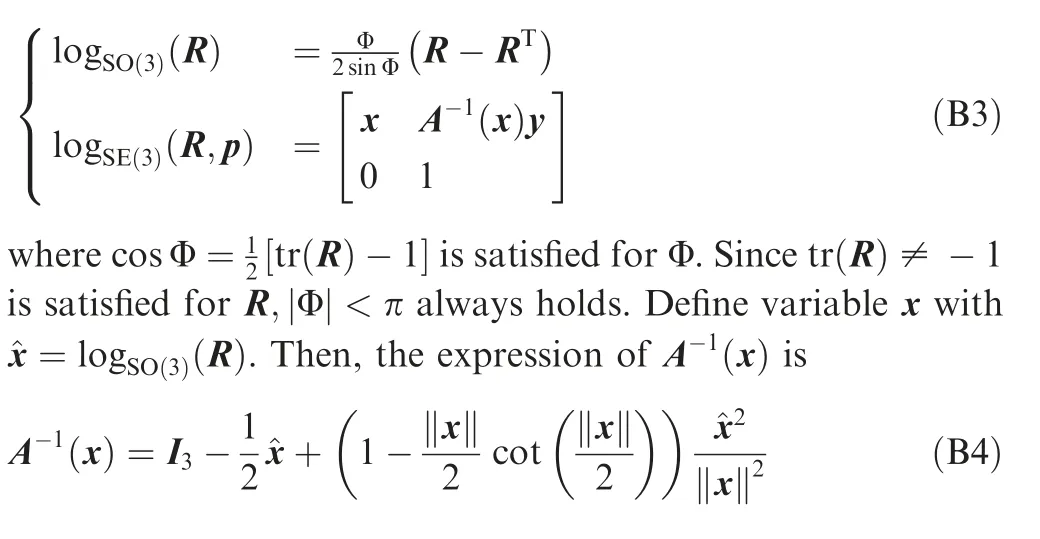Sub-optimal fixed-finite-horizon spacecraft configuration control on SE(3)

Yulin WANG, Wei SHANG, Hicho HONG

a Institute of Remote-sensing Satellite, China Academy of Space Technology, Beijing 100094, China

b School of Mechanical Engineering, Hubei University of Technology, Wuhan 430068, China

c Institute of Flight System Dynamics, Technical University of Munich, Garching 85748, Germany

KEYWORDS Configuration control;Lie groups;Model Predictive Static Programming;Optimal control;Spacecraft control

Abstract For achieving the desired configuration of spacecraft at the desired fixed time, a suboptimal fixed-finite-horizon configuration control method on the Lie group SE(3) is developed based on the Model Predictive Static Programming(MPSP).The MPSP technique has been widely used to solve finite-horizon optimal control problems and is known for its high computational efficiency thanks to the closed-form solution,but it cannot be directly applied to systems on SE(3).The methodological innovation in this paper enables that the MPSP technique is extended to the geometric control on SE(3),using the variational principle, the left-invariant properties of Lie groups,and the topology structure of Lie algebra space. Moreover, the energy consumption, which is crucial for spacecraft operations,is considered as the objective function to be optimized in the optimal control formulation.The effectiveness of the designed sub-optimal control method is demonstrated through an online simulation under disturbances and state measurement errors.

1. Introduction

For space missions, precision control of spacecraft is essential and has attracted considerable attention.The integrated attitude and orbit tracking of a six-degree-of-freedom(6-DOF) spacecraft is one of the key technologies, e.g., for autonomous rendezvous and docking,hovering over an asteroid,and spacecraft formation flying.Compared with the traditional modeling scheme whose attitude and position are modeled separately,the integrated modeling scheme includes the mutual couplings between attitude and position, leading to a higher accuracy.

A 3-dimensional Special Euclidean group (SE(3)) can describe uniquely and globally the integrated attitude and position of a 6-DOF spacecraft in a 3-dimensional Euclidean space. In this modeling scheme, the mutual couplings between attitude and position are considered.In addition,the singularities and ambiguities of attitude representations are avoided.Thanks to these advantages, controlling 6-DOF rigid-body spacecraft modeled on SE(3), which are often referred as ‘‘geometric”control,has been widely researched by pioneers,e.g.,by Bullo and Murray, Lee et al.. In the existing studies, the PD control theory, the sliding mode control theory, and the fixed-time convergence control theoryare applied. Moreover, the control force saturation is considered in Ref. 7. In Ref. 11, a decentralized collision-avoidance control scheme is designed for spacecraft formation flying based on artificial potentials.These geometric control schemes do not consider minimizing the energy consumption.Actually,the stored fuel of an in-orbit spacecraft is usually limited.Therefore, the energy consumption during the maneuver should be optimized to extend the operating life of spacecraft.

Under the general concept of Model Predictive Control(MPC), the energy consumption can be considered.MPC techniques have been applied to the mechanical systems modeled on the Lie group SO(3)and SE(3). However, these optimal control problem on Lie groups in Refs. 22-24 are all constructed and solved based on the linearized equations around their equilibrium points, and the algebraic Riccati equations need to be solved. In the optimal control schemes designed in Refs. 25-28, the nonlinear dynamics on SE(3)are considered.However,in Refs.25,26,the two point boundary value problems need to be solved,which yields a high computational complexity. In Refs. 27,28, only the kinematics characteristics are studied in the optimal controller on SE(3).

Combining the philosophies of Approximate Dynamic Programming(ADP)and MPC,Padhi proposed a finite-horizon optimal control method with hard terminal constraints called the Model Predictive Static Programming (MPSP).The MPSP generates explicit closed-form solutions without relying on numerical optimization solver. Studies based on the MPSP and its varieties have been carried out in fields of aeronauticsand astronautics. However, the commonly used MPSP technique in Ref. 30 and its varieties can only be used to solve an explicit discrete-time nonlinear dynamical system.Since SE(3) is a Lie group and a 6-dimensional manifold, its discrete-time nonlinear dynamical equation obtained from the Lie Group Variational Integrator (LGVI) is implicit.Hence, the implementation of the commonly used MPSP is not yet feasible on SE(3).

This paper develops the intermediate steps that enable the application of the MPSP on SE(3), and thus achieves a suboptimal fixed-finite-horizon control on SE(3), optimizing the overall energy consumption. Firstly, the dynamical equations of the spacecraft modeled on SE(3) are normalized, and thus the state variables on SE(3) have a similar numerical range.Then, based on the variational principle, the left-invariant properties of Lie groups, and the topology structure of Lie algebra space,the MPSP technique is extended to the geometric sub-optimal control on SE(3). The terminal output error between the predicted terminal states and desired states is defined as the exponential coordinate of SE(3). Lastly, taking advantages of the high efficiency, the proposed sub-optimal control scheme on SE(3) is applied online in a shrinking horizon, where the system disturbance and the state measurement errors are considered.Offline and online simulation studies are carried out to demonstrate the effectiveness of the proposed control schemes.

Compared with the MPC designed on SE(3)in Ref.24,the proposed method makes use of the full nonlinear dynamics.Compared with the works in Refs. 27,28, both the kinematics and dynamics of the spacecraft on SE(3)are taken into consideration. Moreover, the proposed sub-optimal control method on SE(3) based on the MPSP has a higher computational efficiency,compared with the two point boundary value problems in Refs. 25,26 and the algebraic Riccati equations solved in Ref.24.Compared with the previous work in Ref.36,the positional dynamics of spacecraft are considered and the MPSP is further applied on SE(3) based on the normalized dynamical equations. Moreover, the terminal output error is designed based on the exponential coordinates of Lie group.

The rest of this paper is organized as follows. In Section 2,the dynamical equations of a 6-DOF spacecraft modeled on SE(3) are given. In Section 3, the proposed sub-optimal control scheme on SE(3) is deduced and designed. In Section 4,the results of numerical simulation are shown. In Section 5,the conclusions of this paper are summarized.

2. SE(3) modeling scheme for spacecraft configuration

In this section, the details of the modeling scheme are presented. The kinematics and dynamics of a fully actuated rigid-body spacecraft are described globally on SE(3). The body-fixed frame and the inertial reference frame are denoted as B-Frame and I-Frame, respectively.

The Lie group SE（3）=SO（3）×Ris the set including the attitude and position.The configuration of a rigid-body spacecraft with respect to I-Frame is denoted as g ∈SE（3）, which can be represented by the following 4×4 matrix as

where τ ∈Rand F ∈Rare input torque and force, respectively. d∈Rand d∈Rare disturbance torque and force,respectively.

Considering the definitions and deductions above,the kinematics and dynamics of 6-DOF spacecraft in Eqs. (4) and (7)are reformulated as Eqs. (11)-(14).

˙R=RΩ（11）˙p=RV（12）J ˙Ω=-Ω×JΩ+τ+d（13）m ˙V=-Ω×mV+F+d（14）

The relative rotation angle between the current and desired attitudes of spacecraft is usually bounded by π rad. However,the relative distance between the current and desired positions is unlimited. In order to ensure a similar numerical range for all state variables, the state variables of the translational subsystem can be normalized as follows

3. Sub-optimal fixed-finite-horizon configuration control based on the MPSP

In this section,a sub-optimal fixed-finite-horizon configuration control on SE(3) is deduced and designed based on the MPSP technique.The general derivations and design processes of the original MPSP on an Euclidean space can be found in Appendix A. However, SE(3) is a six-dimensional nonlinear manifold with 16elements and 10constraints. The general designing procedure of the MPSP in Appendix A cannot be applied on SE(3). This problem will be detailed and resolved by the theory of differential geometry in this section.

3.1. Discrete-time dynamics on SE(3)

Before the sub-optimal control scheme is constructed, the system described by Eq. (16) should be discretized with time.Since SE(3) is a Lie group, commonly used numerical integration methods,such as the Euler integration,cannot preserve its underlying group structure. Therefore, the Lie Group Variational Integrator (LGVI) is applied here to provide the discrete-time nonlinear dynamical system on SE(3). From the continuous dynamical system in Eq. (16), the LGVI-based discrete-time nonlinear dynamics of 6-DOF spacecraft system modeled on SE(3) are expressed as Eqs. (17)-(21)

3.2. MPSP on SE(3)

Because of the implicit LGVI-based discrete-time nonlinear dynamical expression of SE(3) in Eqs. (17)-(21) and the Lie group Rincluded in the state X,the general MPSP technique in Appendix A cannot be applied on SE(3). This subsection provides new insight into applying the MPSP technique on the Lie group SE(3) based on the variational principle, the left-invariant properties of Lie groups,and the topology structure of so（3）.

The terminal output and the desired output of the discretetime system in Eqs. (17)-(21) are denoted as Yand Y,respectively. The primary objective of this paper is designing a suitable control series U，k=1，2，...，N-1 for the discrete-time dynamical system described by Eqs. (17)-(21),in order to let Yreach to Ywith the minimal energy consumption. The optimal control problem is summarized as

Moreover, the infinitesimal variations of the output Y and input U in Eq. (22) are given in Eq. (31) and Eq. (32),respectively.

Similar to the expression of dX，dXcan be also expressed by dXand dU.Repeating this procedure until k=1，dYcan be deduced and expanded as

Fig.1 Nassi Shneiderman diagram for the propagations of Eqs.(17)-(21).

Eq.(43)is structurally similar to the original form which is not directly applicable. However, the new expressions in Eqs. (34)and(35)yield an applicable closed-form solution of the MPSP on SE(3). It can be used to obtain the fixed-finite-horizon energy sub-optimal control with hard terminal constraints for the 6-DOF spacecraft described on SE(3). dYis the predicted terminal output error between Yand Y,and its computation will be elaborated in the next section.

3.3. Definition of dYN

Considering the definition of Yin Eq. (22), dYis the predicted terminal error between （g，ξ） and （g，ξ）. gand ξare the normalized predicted terminal configuration and generalized velocity, respectively, which are obtained by the numerical integration of Eq. (16). Accordingly, gand ξare the normalized desired configuration and generalized velocity,respectively.dYincludes the configuration error e∈Rand the generalized velocity error e∈R,which can be expressed as

Similar to Eq. (49), the generalized velocity error vector eis given by

Fig. 2 Nassi Shneiderman diagram for the implementation of the MPSP on SE(3).

where e∈Rand e∈Rare the angular velocity error vector and the position velocity error vector, respectively.

With the predicted terminal states （g，ξ） and the desired states （g，ξ）, the configuration error eand generalized velocity error eare calculated by Eq. (48) and Eq. (50),respectively. Then, dYin Eq. (46) is obtained.

To this point, the closed-form solution of the sub-optimal fixed-finite-horizon control on SE(3) is obtained based on the MPSP technique. The implementation steps of the proposed sub-optimal control scheme applied to the 6-DOF spacecraft modeled on SE(3) are displayed in Fig. 2. In order to limit the calculation time needed for iterations, the threshold dYand the maximum iteration times K are used in Fig. 2. Therefor, the control scheme is sub-optimal when it is applied in practice.

In order to stabilize the configuration of a 6-DOF spacecraft considering system disturbance and state measurement errors, the proposed sub-optimal control scheme can be applied online in a shrinking horizon.The control strategy is depicted in Fig. 3. The sub-optimal control input U，k=1，2，...，N-1 is updated and computed online by the MPSP based on the measured states at every step between two executions. Moreover, trepresents the predicted horizon, which is diminishing over time, as tis fixed. In addition,t，k=1，2，...，N-1 is the moment when the control input U，k=1，2，...，N-1 is updated, and tdenotes the execution horizon.

4. Simulation

In this section,the results of applying the proposed method to control a rigid-body spacecraft modeled on SE(3) are simulated in a MATLAB environment.The proposed configuration control method is applied in an offline ideal scenario and an online practical scenario.

4.1. Offline results

In order to achieve the set-point maneuvers of a rigid-body spacecraft, the desired configuration of spacecraft is fixed as g=I. The attitude of rigid-body spacecraft is described by theexponentialmapexp:so（3）→SO（3）as R=exp（x）, which is defined in Eq. (B1) in Appendix B. To illustrate the global expression of SO(3), x（0） is set as［-2.49，1.49，-1.12］ with ‖x（0）‖=0.99π, and the initial angular velocity Ω（0） is set as ［0，0，0］. The initial position is set as［-3.6，-3，2］, and the initial position velocity is set as ［0，0，0］.The initial control input series is set to zero as U=0，k=1，2，...，N-1. Disturbances and uncertainties are not considered in this section.

The mass of spacecraft is set as 56.7 kg, and the inertial matrix is set as

The control parameters used are set as those in Table 1.The simulation results are depicted in Figs. 4-6.

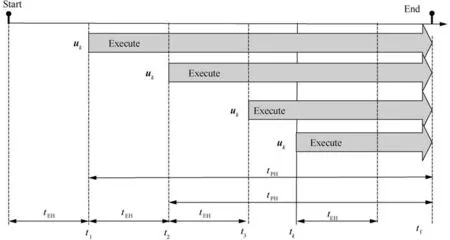
Fig. 3 Control strategy of the shrinking horizon control [36].

Table 1 Control parameters.

Fig. 4(a) shows the configuration error vector echanging versus time. It can be seen from Fig. 4(a) and Fig. 4(b) that the attitude error vector eand the position error vector econverge to zero at the scheduled time t=10 s.

Fig.5 depicts the generalized velocity error vector echanging with time. Fig. 5(a) and Fig. 5(b) show that the angular error vector eand the position velocity error vector econverge to zero at t=10 s. Combined with the results in Fig.4,it can be concluded that the expected set-point manoeuvres can be achieved for rigid-body spacecraft.

Fig.6 depicts the time histories of the optimal control input U.Fig.6(a)and Fig.6(b)show the torque and force of 6-DOF spacecraft changing versus time, respectively.

The simulation results for different initial states are summarized in Table 2. It can be seen that the high accuracy is obtained for the configuration control of spacecraft using the proposed method.

For comparison, the Geometric Proportional-Derivative(GPD) controller designed in Ref. 18 are also simulated in the three cases.The simulation results of the three cases under the GPD are summarized in Table 3. It can be seen that the higher accuracy and less energy cost can be achieved by the MPSP compared with the GPD in Ref. 18.

4.2. Online results

To demonstrate the practical significance, the generalized external disturbance and state measurement errors of spacecraft are introduced. In addition, the MPSP is applied online to stabilize the configuration. In this subsection, combined with the shrinking horizon control, the numerical simulation of the online MPSP are carried out to illustrate its effectiveness.

The disturbance torque of spacecraft is set as

Fig. 4 Offline: Configuration error vector eg changing versus time.

Fig. 5 Offline: Generalized velocity error vector eξ changing versus time.

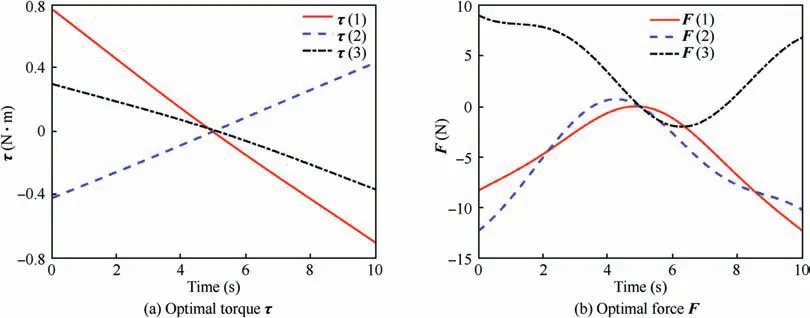
Fig. 6 Offline: Optimal control input U changing versus time.

Table 2 Initial states and results of simulation.

Table 3 Simulation results of GPD.

The measurement error of attitude is expressed by the exponential map of SO(3)in Eq.(B1)in Appendix B.The relationships between the observed states ^R，^p， ^Ω，^V and the actual states R，p，Ω，V are described as

where σ∈R，j=1，2，3，4 are the measurement errors of states. σare the Gaussian noise and satisfy σ（i）～N（0，0.003），i=1，2，3.

The control parameters for the online application are set as follows. The initial length of the shrinking horizon is set as t=10 s. The execution horizon tis 0.1s. The control parameters of the MPSP, the initial and desired states are set the same as those of Case 1 in Section 4.1. The simulation results of the close-loop system are shown in Figs. 7-10.

The configuration error vector eunder the online MPSP changing versus time is depicted in Fig. 7. The time histories of the generalized velocity error vector eare shown in Fig.8.The simulation results in Figs.7 and 8 demonstrate that the error vectors eand eof the closed-loop spacecraft system under the online MPSP converge to zero in scheduled time t=10 s, while disturbances and measurement errors exist.

Fig.9 shows the time histories of the torque τ and the force F of the closed-loop spacecraft system. Compared with the simulation results of the offline MPSP in Fig.6,there are some jitters for the generalized force input in Fig. 9, because of the Gaussian noises of the measured states in Eq. (53). However,the jitters only become noticeable in the terminal period. As the shrinking horizon control strategy is applied here, the length of tdecreases to a small value at the terminal stage.In this period,the same level of disturbances and measurement errors cause more visible changes for optimal control histories.

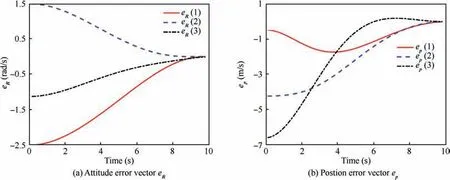
Fig. 7 Online: Configuration error vector eg changing with time.

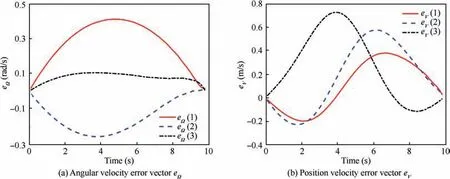
Fig. 8 Online: Generalized velocity error vector eξ changing with time.

Fig. 9 Online: Optimal control input U changing with time.

Fig. 10 demonstrates the configuration trajectory of rigidbody spacecraft changing with time. The spacecraft’s position and the orientation of the body-fixed frame are plotted along the trajectory at 0, 2, 4,6, 8, 10 s, respectively. The configuration of the rigid-body spacecraft controlled by the online MPSP can be stabilized to the desired configuration at the scheduled time t=10 s with a high efficiency (without overshot). It can also be seen that the large-angle maneuver(greater than π/2) can be also achieved without singularity and unwinding phenomena.

It can be seen from Table 2 that the computation time of the offline MPSP in a MATLAB environment is longer than the execution horizon t=0.1s of the online MPSP. However, when the MPSP is applied online, the control series can be iterated and updated based on the results of the previous step. Therefore, the computation time can be significantly shortened and less than t=0.1s, Therefore, the MPSP can be applied online in practice.

Fig. 10 Configuration trajectory of spacecraft under the online MPSP.

5. Conclusions

This paper addresses the sub-optimal fixed-finite-horizon spacecraft configuration control on SE(3) based on the Model Predictive Static Programming (MPSP). The translational dynamical equations are normalized to ensure a similar numerical range for the translational and rotational subsystems of 6-DOF spacecraft. Then, using the variational principle and the geometric property of Lie group, the states’ variation is expressed by an explicit discrete-time form in an Euclidean space, which can be integrated with the MPSP to control the configuration on SE(3) in a fixed horizon. The geometric sub-optimal control leads to promising simulation results with a high accuracy.Moreover,the simulation results of the online application with disturbances and errors demonstrate that the proposed sub-optimal method can stabilize the configuration of a 6-DOF spacecraft in practical scenarios.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

Haichao Hong acknowledges the support of the TUM University Foundation Fellowship.

Appendix A. Model predictive static programming design

In this section,the brief summary of the MPSP are introduced,which can be applied to a nonlinear dynamical system modeled on an Euclidean space. For more details about the MPSP,readers can refer to Refs. 30,31.

To begin, a general nonlinear dynamical system is considered here in a discrete-time form. Its state and output dynamics are given by

In Eq. (A9), there are （N-1）m unknown variables and p linear equality constraints. Since p<（N-1）m, the system described by Eq.(A9)is under-constrained.In order to obtain its unique solution,some additional objectives should be introduced. Such as minimizing the following objective (cost)function

Now, the closed-form solution of the MPSP in an Euclidean space Ris obtained. The MPSP can be used to solve the optimization problem with an explicit discrete-time nonlinear dynamical system like Eqs. (A1) and (A2).

Appendix B. Exponential and logarithmic map

For the Lie groups SO(3) and SE(3), with their Lie algebra so（3） and se（3）, the exponential and logarithmic map is defined below.

Lemma B1. [Exponential Map] Given any Lie algebra^x ∈so（3） and ¯X=（^x，y）∈se（3）, the exponential map on so（3），exp:so（3）→SO（3）, and the exponential map on se（3），exp:se（3）→SE（3） are defined as

Lemma B2. For any given R ∈SO（3）and（R，p）∈SE（3）with tr（R）≠-1 holding for R, the logarithmic maps on SO（3），log:SO（3）→so（3）, and on SE（3），log:SE（3）→se（3）, are defined as