Modified rolling guidance law for single moving mass controlled reentry vehicle against maneuvering target with impact angle constraints

Guanlin LI, Ming YANG, Songyan WANG, Tao CHAO

Control and Simulation Center, Harbin Institute of Technology, Harbin 150001, China

KEYWORDS Reentry vehicles;Guidance law;Impact angle;Maneuvering target;Finite-time convergence

Abstract This paper deals with the problem of guidance law design for the single moving mass controlled reentry vehicle when impact angle constraints and maneuvering target are taken into consideration. More specifically, a modified rolling guidance law is proposed with the interactive virtual target and the landing point prediction strategy.First,considering the fact that the roll channel can be controlled directly,the relative motion between the single moving mass controlled reentry vehicle and the target is described by the error angle between the relative velocity and the line-ofsight. Second, a nonlinear error angle command is given to reduce the rotation rate. To satisfy impact angle constraints, an interactive virtual target is presented and the ‘‘S” formed velocity of the virtual target is given to abate the error angle tracking difficulty at the final stage of the reentry phase. Then, the landing point prediction strategy is employed and the motion variation trend is also taken into consideration. As the maneuvering target is replaced with the predicted landing point, the error angle tracking difficulty caused by the target velocity decreases, which is helpful to meet impact angle constraints and improve guidance accuracy at the same time. Finally, the finite-time rolling guidance law is proposed and proved via Lyapunov stability theorem.Compared with the existing method, lower-speed rotation, smaller missing distance and less impact angle errors are obtained, which can be demonstrated by numerical simulations.

1. Introduction

Single Moving Mass Controlled Reentry Vehicle (SMMCRV)is controlled by the moving mass inside the body. Compared with the conventional rudder controlled and thruster controlled reentry vehicle, it has advantages of faster response,better aerodynamic shape and so on. Therefore, the research on the SMMCRV draws considerable attention of the experts.In the field of moving mass controlled reentry vehicle, some works have been undertaken in past decades. Moving Mass Trim Control(MMTC)was presented in 1996 and the characteristic of the aerospace vehicle was discussed by the test.Petsopoulos established the dynamics model for the SMMCRV and designed the controller based on the linear system.Then,MMTC technology has also been applied in other areas.In spite of aforementioned advantages and applications, underactuated characteristic generated by the single moving mass is nonnegligible. To be more specific, the traditional guidance law design based on the vertical plane and the lateral plane is not suitable for SMMCRV.For the design of the guidance law for the SMMCRV, the main difficulty is the contradiction between the high accuracy guidance demand and the uncontrollable lift force of the SMMCRV. To trade off the contradiction, the relative motion model has been established and the error angle was employed to describe the relative motion between the SMMCRV and the target.Based on the relative motion model, the rolling guidance law was proposed.

Apart from the high precision,impact angle is an important factor which influences the attack effectiveness of the vehicle.To satisfy the terminal impact-angle constraints, some works have been done over the past years. Some alternative methods or theories are applied in the guidance law design for the reentry vehicle with impact angle constraints,including optimal theory based method,sliding mode control,adaptive control,back-stepping controland so on. Yet the aforementioned works mainly focus on the relative motion described by the line-of-sight angle and its rate,which is not suitable for SMMCRV.Considering the under-actuated characteristic of the SMMCRV,the novel strategy needs to be adopted.Based on the idea of the rolling guidance law,the virtual target is introduced into the guidance law.However, the guidance law in Ref.21 is suitable for the SMMCRV with low speed based on the assumption that the aerodynamic coefficient is constant.

From the view of engineering application, the target is not always fixed on the ground.Guidance law design for the reentry vehicle against the maneuvering target is also a field of interest.In the existing works, the maneuvering target is always regarded as the disturbance in the guidance system.The guidance law was presented based on the prescribed performance sliding mode against maneuvering targets.Zhang designed the guidance law based on the fixed-time convergence theory and adopted it on the intercepting maneuvering targets with angle constraint.Due to the fact that the lift force magnitude of SMMCRV is uncontrollable, the method of including the motion information of the target in the guidance law causes difficulty of error angle convergence and the guidance accuracy is reduced. Therefore, the aforementioned methods cannot be applied to the SMMCRV directly. Based on the above analysis, the guidance law design for the SMMCRV against the maneuvering target with the desired impact angles still deserves research from the view of theory and application.

In this paper, a modified rolling guidance law with the virtual target is proposed, addressing the issue of the SMMCRV guidance system design against the maneuvering target with impact angle constraints. Contributions of this paper can be described specifically as follows:

(1) Considering the characteristic of uncontrollable magnitude of the lift force,a novel nonlinear,continuous error angle command is proposed, which is easier to be tracked with lower roll rate.

(2) A nonlinear interactive virtual target is employed in the guidance system to satisfy impact angle constraints.Considering the maneuverable of SMMCRV, an ‘‘S”formed virtual target velocity is given and the trajectory is derived. In addition, the feedback term is added into the virtual target to reduce the errors of impact angles.Compared with the fixed-proportion virtual target,impact angle errors get smaller and the guidance system is suitable for more impact angle combinations.

(3) For solving the problem of tracking the maneuvering target, a landing point prediction strategy is proposed.For obtaining the predicted landing point, the acceleration of the target is estimated by the numerical form method. The concept of ‘‘equivalent acceleration”described by the weighted combination of the historic acceleration, the current acceleration and the acceleration variation trend is proposed and the weight updating strategy is given. The difficulty of error angle command tracking caused by the maneuvering target decreases when the actual target is replaced by the predicted landing point.Compared with the traditional method,higher accuracy is obtained, especially for the reentry phase with the impact angle constraints.

The rest of this paper is organized as follows:The dynamics model of the SMMCRV and the relative motion model are established in Section 2. The basic idea of the guidance law is given in Section 3, including the principle of the guidance strategy, the path design of the virtual target and the prediction of the landing point. In Section 4, the modified rolling guidance law is proposed and the stability of the guidance system is proved via Lyapunov stability theorem. To testify the performance of the guidance law, numerical simulations are carried out in Section 5 with some discussions.The conclusions are drawn in Section 6.

2. Problem formulation

2.1. Dynamics model of SMMCRV

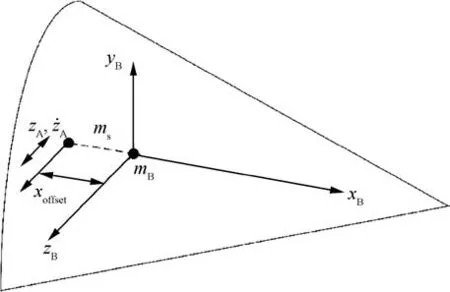
Fig. 1 Structure of Single Moving Mass Controlled Reentry Vehicle (SMMCRV).

The structure of the SMMCRV is illustrated in Fig. 1. Controlled by the single moving mass inside the body, the SMMCRV mainly consists of two parts: the moving mass mand the body m. The single moving mass runs along the slide rail parallel to the z axis of the body coordinate system.zand ˙zrepresent the position and the velocity of the moving mass, respectively. As the SMMCRV is controlled by the single moving mass merely, only roll angle can be controlled directly, leading to the fact that the SMMCRV system is under-actuated.

To establish the dynamics model of the SMMCRV, some assumptions are made:

(1) The earth is flat and the inertia force caused by the earth rotation is ignored.

(2) The angle of attack α is trimmed and the nonlinear function α=α=f （mach） is met.

(3) As the mass ratio m/（m+m） is small, the inertia forces generated by the moving mass velocity and acceleration are ignored.

Based on the above assumptions, the 3-DOF dynamics model of the SMMCRV can be characterized as.

2.2. Relative motion model

Considering the under-actuated characteristic of the SMMCRV, the relative motion between the SMMCRV and the target is illustrated in Fig. 2 and the error angle is employed.

Some definitions are employed to describe the relative motion between the SMMCRV and the target.

(1) Error angle η : the angle between the velocity vector V and the line-of-sight l.

(2) Error plane MPNQ : the plane consists of the velocity vector V and the line-of-sight l.

(3) Error coordinate system Mxyz: the origin is the centroid of the SMMCRV M;Mxcoincides with the velocity vector V; Myis in the error plane and is perpendicular to Mx; Mzis determined by the right hand rule.Then,the derivate of the line-of-sight vector l can be written as

where δ（·）/δt is the derivative in the error coordinate system;ω is the rotation vector between the error angle coordinate system and the trajectory coordinate system.

As the overload generated by the aerodynamics force is far larger than that caused by the gravity,the terms gand gcan be regarded as disturbance and the simplified form of the relative motion model can be written as

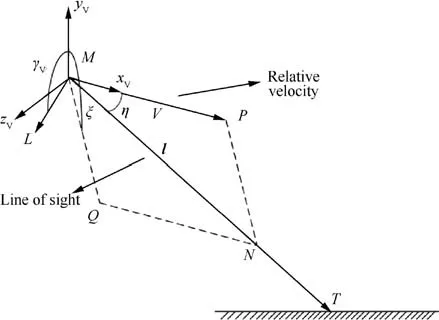
Fig. 2 Relative motion between SMMCRV and target.

3. Construction of the guidance system

According to Fig.3,the guidance system mainly consists of three parts:Modified Rolling Guidance Law(MRGL),Virtual Target(VT)with Interactive Strategy(IS),and Landing Point Prediction(LPP).For the reentry phase against maneuvering targets with time-varying acceleration,the LPP is proposed to identify the motion described by the weight and provide the prediction of the landing point of SMMCRV. Considering the underactuated characteristic and the maneuverability of the SMMCRV,the VT is employed in the guidance system to satisfy the impact angle constraints. Then, the velocity of VT is presented and the analytic form path is derived.After that,the relative motion between VT and SMMCRV is taken into consideration and the modified rolling guidance law is obtained.

Remark 2. It can be found from Fig. 3 that the input of the relative motion model contains the motion information of VT,instead of the actual target motion information.

3.1. Interactive strategy based virtual target design

Demonstrated from Fig. 3, two strategies are employed in the guidance system: the landing point prediction and the interactive virtual target. These two parts serve for the maneuvering target and impact angle constraints, respectively. As a result,the performance of SMMCRV against the maneuvering target is improved.

Considering the relative motion between SMMCRV and the target, different kinds of the virtual target path can be obtained. It can be noted from Ref. 28 that the SMMCRV rotation gets more intense when the distance between the SMMCRV and the target decreases. Considering the limited maneuverability of the SMMCRV, the constant velocity of the virtual targets seems less suitable. Similarly, the constant proportional relation between the virtual target velocity and the SMMCRV velocity brings tracking difficulties when the high-speed reentry is taken into consideration. Based on the above analysis, an ‘‘S” formed velocity curve of the virtual target velocity is proposed. As the initial altitude and the final altitude are known for every certain flight, the altitude h is chosen as the independent variable and the time-varying velocity of the interactive virtual target can be written as

where f（·） and f（·） are designed functions; θand ψare the desired impact angles; Δθand Δψare the errors of impact angles; k>0 is the constant parameter.

Then,the position of virtual target with interactive strategy can be obtained:

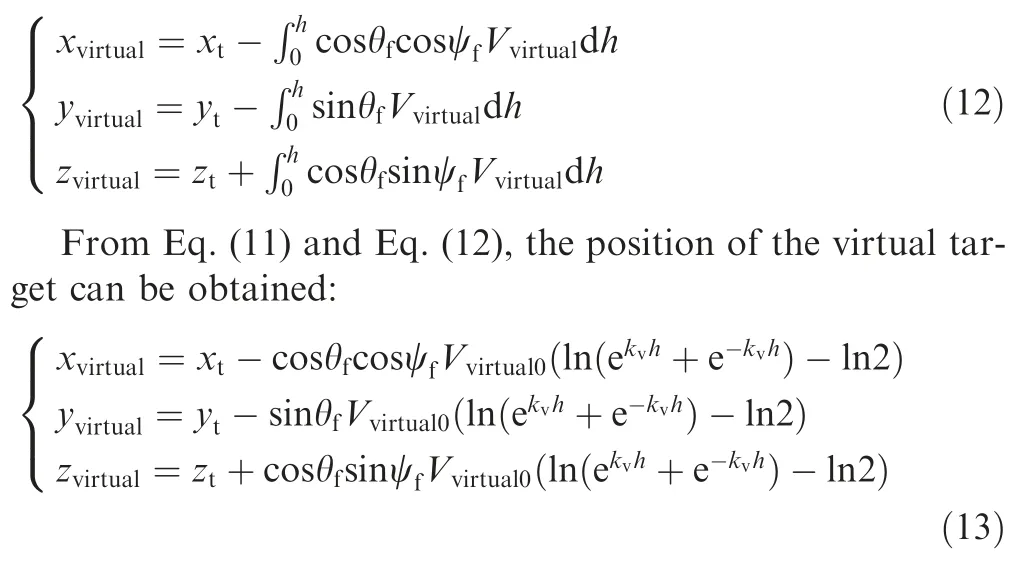
It can be noted that the position of the interactive virtual target is the same as that of the actual target when the SMMCRV reaches the ground. Therefore, the accuracy of the guidance system can be guaranteed when the SMMCRV tracks the virtual target.

Remark 3. The parameter kplays an important role when the tracking performance is taken into consideration.The velocity of the virtual target decreases fast when kis too large and impact angle errors grow.On the other hand,too small kadds the difficulty of error angle convergence and results in poor guidance precision. The value of kis determined by initial altitude of the reentry phase and the velocity of the SMMCRV and adjusted by experience or simulation results.

3.2. Landing point prediction

It can be known from Eq. (9) that the relative velocity has great influence on the convergence process of error angle and the guidance system accuracy.As an effective method to abate the aforementioned influence, the landing point prediction is proposed.The structure of the landing point prediction is presented in Fig. 4.

The motion estimation process mainly includes three steps:Step1. acceleration estimation: numerical acceleration obtained by the target position and rolling updating strategy are introduced to reduce the influence caused by the random term or the high-frequency term of the target time-varying acceleration; Step 2. acceleration array analysis: the feature of the acceleration array is achieved and analyzed, providing the estimated ‘‘equivalent acceleration” by the weighted combination of the historic,current and variation trend of the target acceleration; Step 3. landing point prediction: by combining the results of Step 1 and Step 2, the landing point of the SMMCRV is estimated and updated during the whole reentry phase.

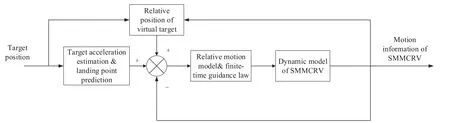
Fig. 3 Structure of guidance system for SMMCRV.

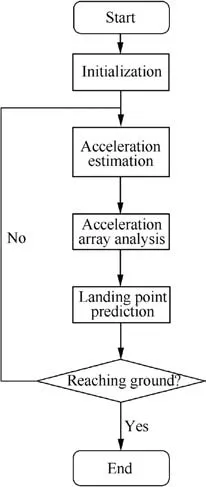
Fig. 4 Flowchart of maneuvering target motion estimation.

As the angles of sight and the relative distance between the SMMCRV and the target can be obtained during the reentry phase, the position of the target can be calculated when the position of the SMMCRV is given by the inertial system.Therefore, the time-based position array of the target can be described as

Remark 4. Considering maneuvering targets in this paper mainly include cars or vehicles moving on the ground, the acceleration is bounded and slowly time-varying.On the other hand, the time interval between adjacent sampling points is always smaller than 0.01 s. Therefore, the acceleration variation can be ignored and Eq. (17) holds.

To demonstrate the performance acceleration estimation,two different motions are chosen and the parameter n is set as 5,10 and 15.The error between the estimation acceleration and its real value is shown in Table 1.

Remark 5. The parameter n is important for the acceleration estimation. Too small value chosen causes the insufficient information,reducing the prediction accuracy.Too large value chosen means the long time span and the assumption is difficult to meet.

However, the acceleration of the maneuvering target is time-varying in practice. Therefore, a strategy is proposed for improving the estimation performance. Two factors are taken into consideration: (A) the volatility of the acceleration;(B)the magnitudes of the current acceleration and the historic acceleration of the target. For describing factors quantificationally, two variables F, Fare employed as follows:

where parameters k（i=1，2，3，4，5）>0 are constant;ξ，ξare the outputs of the evaluation system.

Therefore, the ‘‘equivalent acceleration” aand predicted landing point along x axis can be obtained:

Table 1 Comparison result of acceleration estimation.

Remark 6. Parameters k（i=1，2，3，4，5） in Eq. (24) have influence on outputs of the evaluation system. The parameter selection principle is based on the variation trend of target acceleration, which is determined by the motion form of the target. The initial values of kare always set as 1 and some adjustments are made as needed. For example, larger kand smaller kare chosen when the random term of acceleration needs to be taken more attention to.

Similarly, two inputs of the evaluation system in the z axis direction and the predicted position of the target along z axis can be obtained.

As maneuvering targets in this paper mainly include tanks or armored vehicles moving on the ground, the motion along y axis is passive,which is determined by the terrain.Therefore,the landing point prediction along y axis can be obtained by position array y. Similar to the prediction method in Eqs.

3.3. Error analysis of landing point prediction

To analyze the error of the landing point prediction, the error between the ‘‘equivalent acceleration” and its estimation is defined as e.It can be known that the landing point can be predicted when the error converges to zero. Taking the motion along x axis as an example,error analysis is given and different cases are taken into consideration.

(1) The acceleration is constant: obviously, the current acceleration and the average value of the historic acceleration array are almost the same and the inputs of the evaluation system are zero. It can be known from Eq.(24) that outputs ξand ξwill converge to 0.5 and 0, respectively. As the error of acceleration can be close to zero,the error econverges to zero and the prediction of the landing point can approximately represent the real landing point.

(2) The acceleration is time-varying and the variation is bounded: in this case, the influence caused by the acceleration cannot be ignored. As a result, Fworks in the updating system and the output ξgrows to the new equilibrium point,which is between 0.5 and 1.However,the variable Fis still zero because of the bounded acceleration and the output ξkeeps zero. Then, the error ecan be described as

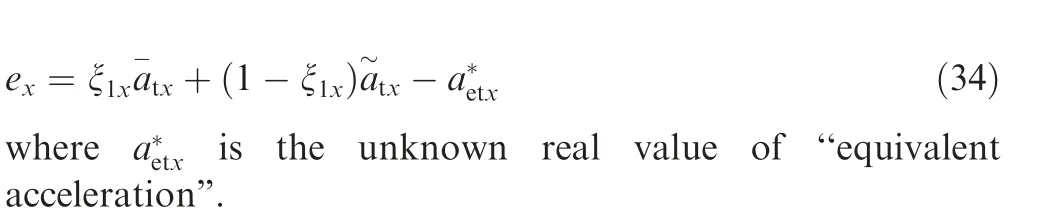
Though the landing point prediction is conservative when the weight of historic acceleration average grows, the chattering caused by the random term or the high-frequency term can be restrained. On the other hand, the error is bounded in this case because of the bounded variation of acceleration.Remarkably, the main goal of the landing point prediction strategy is abating the influence on guidance system caused by the motion information of the target.

(3) The acceleration is rapidly increasing: different from case 2, the maximum or minimum acceleration cannot be obtained until the SMMCRV reaches the target. In this case, the error ecan be written as

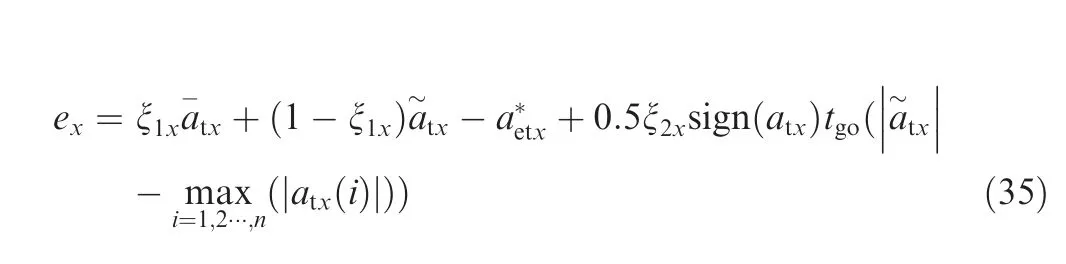
For improving the accuracy of the ‘‘equivalent acceleration” estimation, the variation trend of the acceleration is characterized by F, having influence on outputs ξand ξ. On the one hand, ξdecreases with the term -kξin Eq.(24),which means that current acceleration becomes more important than the historic value. On the other hand, acceleration variation trend is added into landing point prediction and ξis no longer zero. Therefore, the ‘‘equivalent acceleration” estimation can be closer to the real ‘‘equivalent acceleration”.

4. Modified rolling guidance law

The modified rolling guidance law is proposed in this section.The strategy of the guidance law is illustrated in Fig.5 and the aims of the interactive virtual target and the landing point prediction are meeting the impact angle constraints and guaranteeing the guidance accuracy for the SMMCRV at the same time. According to different kinds of maneuvering targets,the structure of the guidance system varies. When the target is fixed on the ground,the virtual target with interactive strategy is employed in the rolling guidance law, satisfying the impact angle constraints.On the other hand,the landing point prediction is added into the guidance system when the maneuvering target is taken into consideration.

4.1. Derivation of guidance law

After that,the line-of-sight vector l between the SMMCRV and the interactive virtual target can be calculated.

Define

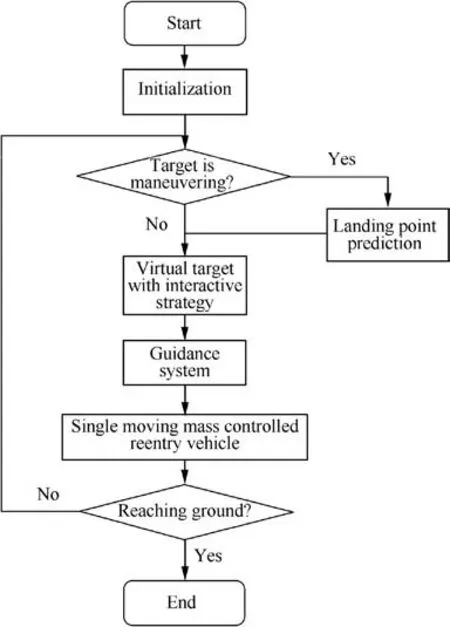
Fig. 5 Flowchart of guidance law.

Table 2 Design parameters of SMMCRV guidance system.

Remark 7. Parameters k and αmainly have effect on the convergence speed of error angle. However, too large value of k and too small value of αmay cause chattering when the SMMCRV is close to the target. Therefore, it is important to choose proper parameters k and αto improve the guidance system performance.

4.2. Stability analysis

5. Numerical simulation

To testify the performance of the guidance system of SMMCRV, numerical simulations are carried out in this section. The initial velocity and altitude of the SMMCRV are 7 000 m/s and 20 000 m, respectively. The initial flight path angle and heading angle are-10and 0,respectively.In addition,design parameters of the SMMCRV guidance system are listed in Table 2.

5.1. Guidance system performance against fixed target

Missing distance with different error angle commands are 0.54 m, 2.18 m and 0.07 m. Compared with the constant error angle command, the error angle command proposed in this paper can reach zero or small value when the SMMCRV reaches the ground,which means that the accuracy of the guidance system can be guaranteed. The error angle tracking performance and bank angle curves are presented in Fig. 6. The small value error angle command does not last for a long time,and the high-speed rotation gets weaker, which is helpful for improving the stability of the guidance system.

Then, five combinations of desired impact angle are given to testify the performance of the guidance system when the fixed target and the impact angle constraints are taken into consideration. In addition, comparative simulations are carried out with the virtual target proposed in this paper(MRGL)and in Ref. 35 (NRGL). Different combinations of impact angle θ, ψare given as follows: Case 1: (-30°, 0°); Case 2:(-45°, 0°); Case 3: (-60°, 0°); Case 4: (-45°, -10°); Case 5:(-45°, +10°).

As depicted by Fig. 7, trajectories vary with different desired impact angles.Desired heading angle mainly has influence on the lateral motion of SMMCRV, which can be noted from Fig.7(a)that lateral motion of Case 1-Case 3 are weaker than those of Case 4 and Case 5. It can be known from Fig.7(b) that higher rotation is needed when the impact angle constraints are taken into consideration, which also proves that the proposed nonlinear error angle command (39) is helpful and necessary. In addition, different desired flight path angles also have influence on the rotation rate of the SMMCRV and the rule can be summarized as follows: the smaller the desired flight path angle, the higher the roll rotation.

It can be noted from Table 3 that the errors get smaller with the interactive virtual target proposed in this paper.Main reasons can be found as follows:(A)Feed-back term provides the adjustment for the SMMCRV,which is helpful to improve the performance of the reentry phase with different impact angle constraints.(B)The velocity of the virtual target is much smaller than that in Ref. 35, which means that the error angle tracks the command more easily, especially for the highspeed SMMCRV.

5.2. Guidance system performance against maneuvering target

To testify the performance of the guidance system against the maneuvering target with impact angle constraints, the impact angle combination is set as θ=-45, ψ=-10, and four kinds of maneuvering target are given in Table 4.

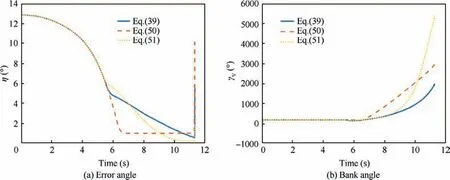
Fig. 6 Comparison results with different error angle commands.

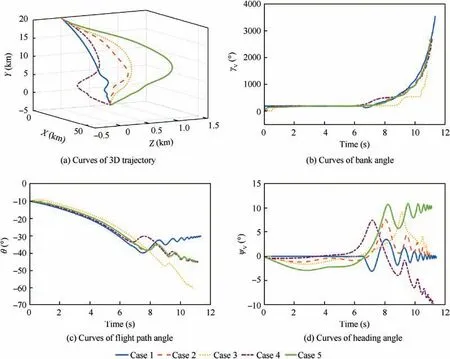
Fig. 7 Simulation results with different impact angle constraints.

Table 3 Comparative simulation results with impact angle constraints.

Table 4 Motion information of maneuvering targets.

where v, vare target velocities in error coordinate system.

As displayed in Figs. 8-11, the outputs of the evaluation system describe the volatility and the variation trend of target acceleration. When the acceleration is constant or zero in Case6, the volatility is weak and the variation trend is not obvious. Outputs ξ=0.5 and ξ=0 mean that the weights of the historic acceleration and the current acceleration are the same. On the other hand, the weight of historic acceleration gets larger when the acceleration is time-varying and bounded. As the weight of historic acceleration grows, the acceleration volatility caused by the noise or periodical change term is restrained. As a result, the ‘‘unnecessary volatility” of the predicted landing point can be avoided, which is helpful for improving the guidance system performance. Terminal state errors of comparative simulations are illustrated in Table 5.

When the influence caused by the terrain is ignored in Case 6 and Case 7, errors Δθ, Δψand the missing distance are smaller than 0.5°, 0.5° and 0.5 m, respectively, which means that the performance of the guidance system is improved with the predicted landing point.As the acceleration of the target is high-frequency periodic,the motion scope gets smaller in Case 8.Therefore,simulation results are approximate in this case.In Case 9, time varying acceleration, random term and terrain influence are taken into consideration. As the weight ξis larger than 0.7, the historic acceleration dominates the ‘‘equivalent acceleration”. As a result, historic acceleration makes the prediction more conservative and the missing distance grows.However,impact angle constraints can be satisfied better when the ‘‘unnecessary volatility” of the predicted landing point is restrained.

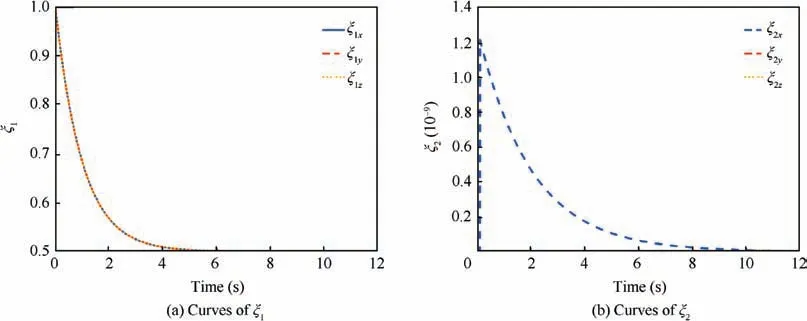
Fig. 8 Curves of evaluation system output with maneuvering Target 6.

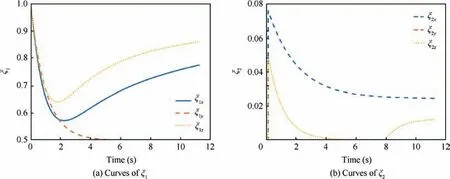
Fig. 9 Curves of evaluation system output with maneuvering Target 7.

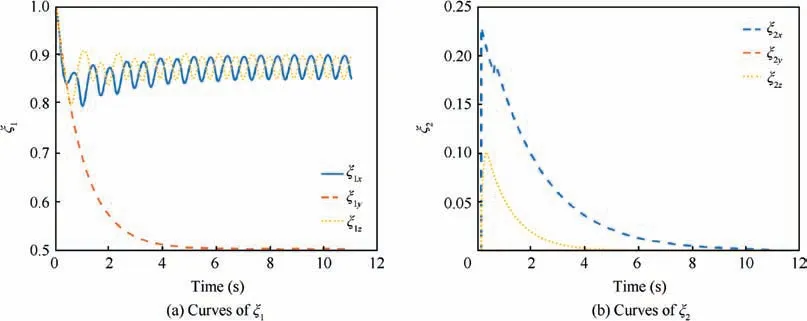
Fig. 10 Curves of evaluation system output with maneuvering Target 8.

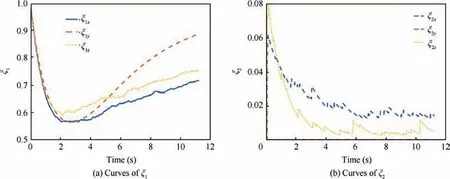
Fig. 11 Curves of evaluation system output with maneuvering Target 9.

Table 5 Comparative simulation results with different maneuvering targets.

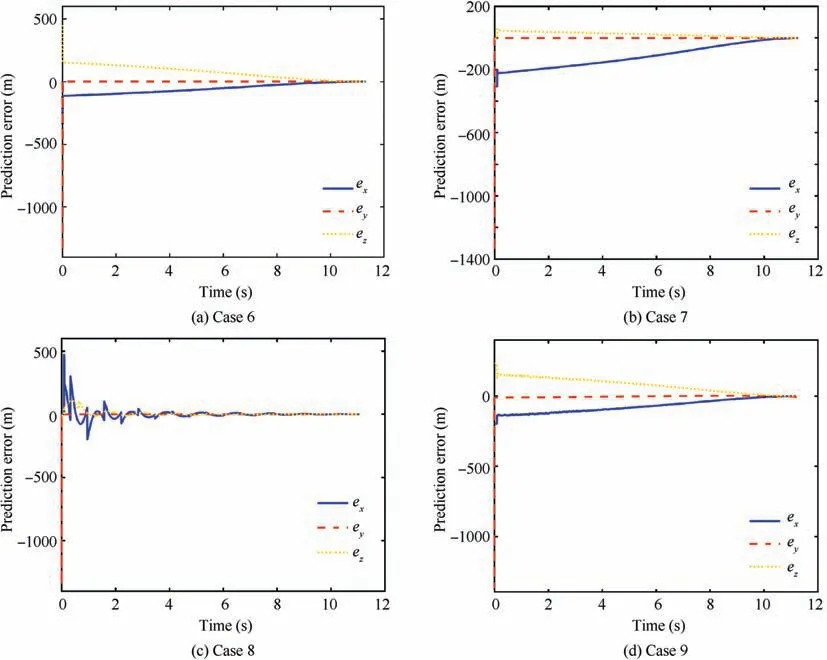
Fig. 12 Landing prediction error for different maneuvering targets.

The landing point prediction error is illustrated in Fig. 12.It can be known that errors decrease in general and converge to small value at the final stage of the reentry phase,achieving the goal of restraining the influence on the guidance system caused by the motion of the maneuvering target. Another important factor that has influence on the landing point prediction is time-to-go (t) calculation. The calculation of tis based on the assumption of constant velocity and error angle, but they are time-varying during the reentry phase. As a result, the prediction error caused by this factor cannot be avoided. However, the influence on the guidance system performance caused by the time-varying velocity is not obvious.On one hand,the main application of tis predicting the landing point and abating the influence on the error angle convergence caused by the maneuverability of the target. As the velocity decreases during the flight, the estimation value of tby t≈l/（Vcosη） is smaller than the real value, which means that the predicted landing point is between the realtime target and the actual landing point.As a result,the aforementioned goal of landing point is achieved and the ‘‘relative maneuverability” of the target is reduced. On the other hand,the main difficulty of the error angle convergence caused by the maneuverability of the target always occurs when the SMMCRV is close to the target. Illustrated by Fig. 12, the error of landing point prediction decreases to a small value,which means that the performance of the guidance system against maneuvering target can be guaranteed with the landing point prediction strategy proposed in this paper.

5.3. Guidance system performance with uncertainties

Considering uncertainties during the reentry phase, Monte-Carlo numerical simulations are carried out,and uncertainties include axial force coefficient ΔC(±10%),normal force coefficient ΔC(±15%), atmospheric density Δρ (±10%), and total mass Δm(±5%).

Fig. 13 shows the distributions of the terminal state. The maximum deviation of missing distance,flight path angle error and heading angle error are less than 8 m, 1.2° and 1.5°,respectively. Considering the sizes of the SMMCRV and the target, the SMMCRV can track the maneuvering target effectively.

As shown in Table 6, average values of Δθ, Δψand missing distance are almost the same as those in Table 5. In addition, small standard deviations demonstrate that the influence on terminal states caused by uncertainties is not obvious and the proposed guidance system of SMMCRV is robust.

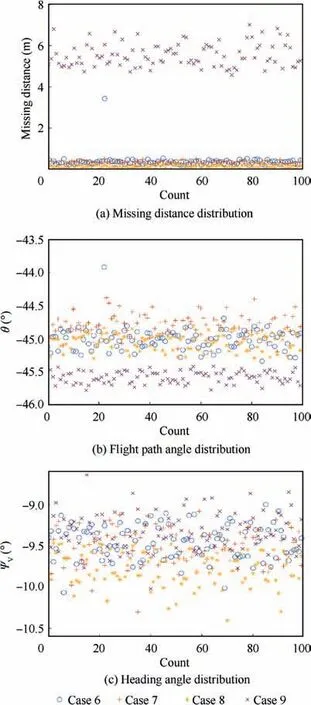
Fig.13 Terminal state distribution of Monte-Carlo simulations.

Table 6 Monte-Carlo simulation results with different maneuvering targets.

6. Conclusions

In this paper, a modified rolling guidance law is proposed to solve the problem of the SMMCRV guidance system against maneuvering target with impact angle constraints. As the actuator of SMMCRV is merely the single moving mass, only roll channel can be controlled directly. For satisfying the impact angle constraints, an interactive virtual target is proposed, solving the problem brought by the under-actuated characteristic. With the nonlinear error angle command,lower speed rotation can be achieved to cut down the stability risk caused by high-speed rotation. Then, the strategy of landing point prediction is employed when the target with time-vary acceleration is taken into consideration. By decreasing the demand of maneuverability, the performance of the guidance system improves when impact angle constraints and maneuvering target are taken into consideration.Finally, the performance of the proposed guidance system is proved via the theoretical analysis and testified by numerical simulations.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This study was supported by the National Natural Science Foundation of China (Nos. 61627810, 61790562, 61403096).