GroupNet: Learning to group corner for object detection in remote sensing imagery

Lei NI, Chunlei HUO, Xin ZHANG, Peng WANG, Zhixin ZHOU,*

a Space Engineering University, Beijing 101416, China

b National Laboratory of Pattern Recognition, Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China

c Beijing Institute of Remote Sensing, Beijing 100192, China

KEYWORDS CornerNet;Feature representation;Multi-dimension embedding;Object detection;Remote sensing

Abstract Due to the attractive potential in avoiding the elaborate definition of anchor attributes,anchor-free-based deep learning approaches are promising for object detection in remote sensing imagery. CornerNet is one of the most representative methods in anchor-free-based deep learning approaches.However,it can be observed distinctly from the visual inspection that the CornerNet is limited in grouping keypoints, which significantly impacts the detection performance. To address the above problem, a novel and effective approach, called GroupNet, is presented in this paper,which adaptively groups corner specific to the objects based on corner embedding vector and corner grouping network. Compared with the CornerNet, the proposed approach is more effective in learning the semantic relationship between corners and improving remarkably the detection performance.On NWPU dataset,experiments demonstrate that our GroupNet not only outperforms the CornerNet with an AP of 12.8%, but also achieves comparable performance to considerable approaches with 83.4% AP.

1. Introduction

Object detection aims to locate the object position and identify the object type in an image,which has considerable impact on various applications, such as remote sensing, video surveillance, automatic driving, etc. With the development of deep learning,object detection has achieved great progressin many challenging benchmarks.Generally, deeplearning-based object detection approaches can be divided into two types, namely anchor-based approach and anchor-free approach. The difference between these two types mainly lies in whether the objects are located by anchors. Despite the above difference, the object locating is very important for all approaches since its impacts will be propagated to the feature classification step.In this context,object region locating is the bottleneck for object recognition. Next, those state-of-the-art detectors focusing on this important topic are briefly reviewed.

The anchor-based approach selects a set of rectangles,which have predefined attributes (e.g., sizes and height-width ratios) and are named as anchors, in an image. And the network refines the anchor locations driven by the regression loss.In the current research of the anchor-based approach, there are usually two kinds of methods, namely two-stage object detectors and one-stage object detectors. Two-stage object detectorsexplicitly extract bounding box candidates and separately classify candidate-related features. Considering the importance of object proposals, many novel strategies have been proposed, e.g., utilizing multiple scales,gaining more contextual information,selecting better features,improving speed,cascade procedure,better training procedure,architecture design,etc. One-stage detectors unify candidate region detection and feature classification. For instance,YOLOv2predicts the position and label on dense grid cells.SSDutilizes feature maps from multiple different convolution layers to classify and regress anchor boxes with different strides. One-stage detectors are inferior to the two-stage ones until the appearance of RetinaNet. RetinaNet proposes the focal loss to balance positive and negative anchors. To mitigate the imbalance issue, RefineDetlearns to early reject well-classified negative anchors.

In contrast, anchor-free detectors choose candidate objects without an anchor.CornerNetlocates an object by a pair of keypoints of the bounding box, the top-left corner and the bottom-right corner. ExtremeNetpredicts four heatmaps for extreme points and one center heatmap for object category.The FCOStrains the network by predicting whether each point of the positive samples is the ground-truth center-point of the object, while the CenterNetpredicts directly the center-point alone instead of each point of the positive samples. Thus, CenterNet is a special case of FCOS essentially.Besides, they all regress the location by the distance between the bounding box and the center point, or by the length and width of the bounding box.

Despite the promising performance of those anchor-based methods, the scales or aspect-ratios of anchor boxes need to be carefully designed to fit the target object. In the practical applications, it is difficult to predefine the accurate information of anchor boxes, especially when the sizes of objects are distributed irregularly.To improve it,the CornerNet proposes a novel method to represent a bounding box as a pair of corners,i.e.,top-left corner and bottom-right corner.However,it is a pity that the CornerNet is hindered by the keypoint grouping technique. As shown in Fig. 1 (a), owing to the negative effect caused by cluttered background and the outliers, many corners are grouped wrongly by CornerNet due to the limitation of one-dimension embedding for feature representation,which results in failed location and further degrades the subsequent object-type identification.

To address the above difficulties, GroupNet is proposed in this paper. As shown in Fig. 1 (b), with the help of adaptively grouping corner based on multi-dimension embedding and corner grouping network, the errors caused by CornerNet are effectively corrected by the proposed approach. The key contributions of this paper are summarized as follows:

(1) Multi-dimension embedding vector generation is presented to enrich semantic relationship between corners,which is very helpful for the subsequent keypoint aggregation.

(2) Dynamic random sample choosing is adapted for multidimension embedding vector, which is useful to balance efficiency and performance.

(3) Corner grouping network is proposed to effectively aggregate the top-left corner and the bottom-right corner. By taking advantage of the corner grouping network, the corner aggregation performance and the detection performance are improved.

2. GroupNet

2.1. Overview

The goal of the proposed GroupNet is to reliably capture the semantic relationship between the top-left and the bottomright corners by data-driven learning. To clarify the novelty of the proposed approach, GroupNet and CornerNet are shown and compared in Fig. 2. It can be founded from Fig.2 that both approaches consist of corner prediction(Block 1) and corner grouping (Block 2). GroupNet and CornerNet share the common corner prediction, which generates two kinds of heatmaps: one is about the top-left corner and the other about the bottom-right corner. The heatmaps represent the location and confidence score of keypoints.

The difference between GroupNet and CornerNet lies in corner grouping. Corner grouping in GroupNet consists of multi-dimension embedding vector generation (Block 3),dynamic random sample choosing(Block 4)and corner grouping network(Block 5),while CornerNet adopts one-dimension embedding vector(Block 6)and chooses all data for loss computation (Block 7). eand erepresent the multi-dimension embedding vectors of the top-left and the bottom-right corner of object k.

Fig. 1 Illustration of keypoints grouping importance.

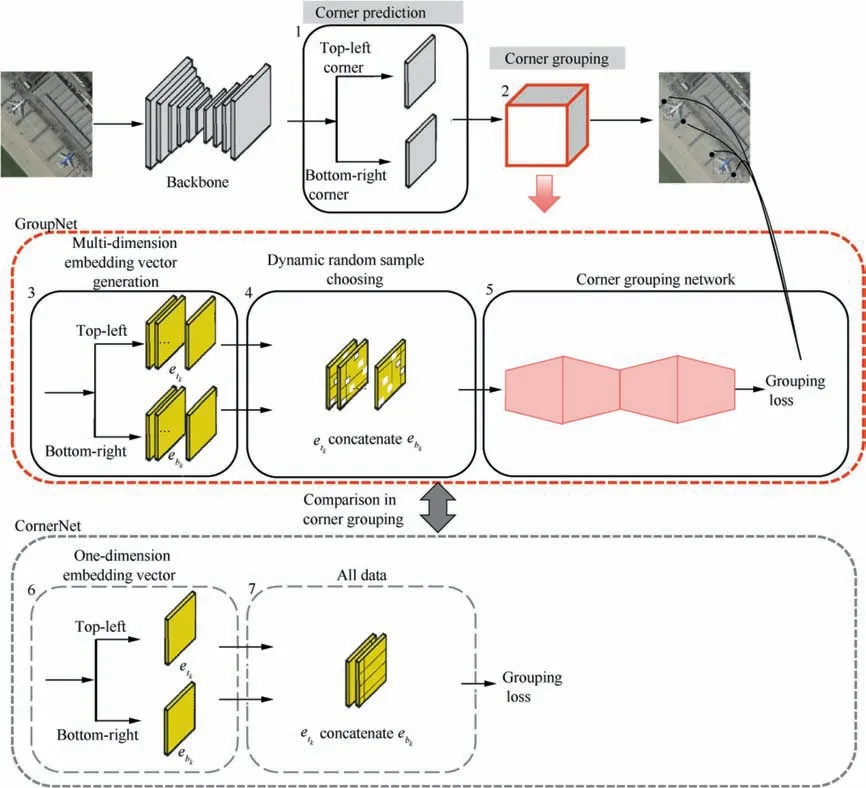
Fig. 2 Architecture comparison of GroupNet and CornerNet.

The main difference between CornerNet and GroupNet lies in corner grouping. In detail, CornerNet just generates lowdimension embedding vector for each corner and produces the bounding box by grouping corner with respect to the distance between embedding vectors. As illustrated in Fig. 1,the ability of the low-dimension embedding vector is limited in representing latent relationships between corners, and this simple grouping rule is inadequate to deal with objects of different sizes, which prevents CornerNet from taking advantage of anchor-free potentials.

To address the above limitations, three modifications are made to enhance CornerNet in this paper. The first modification is multi-dimension embedding vector generation, which helps to capture sufficient and representative features of topleft and bottom-right corners. The second modification is about training samples selection, which is more robust to the imbalance between N positive samples and N（N-1） negative samples and also useful to balance efficiency and performance.The third modification is end-to-end corner grouping network,which is more effective in reducing impacts by weak-heuristic grouping rules. It is the above differences that make the proposed GroupNet more effective and robust. In the following,the above differences will be elaborated step by step.

2.2. Multi-dimension embedding vector generation

After predicting heatmap, offset, and one-dimension embedding, CornerNet matches corner by the distance between the top-left and bottom-right embeddings. The corner information taken by CornerNet is expected to be rich for grouping. However, as shown in Fig. 1, the average precision and recall are not satisfying with respect to corner grouping. The underlying reason is that the one-dimension embedding is too simple to represent rich semantic relationships between corners.Furthermore,it impacts the subsequent corner grouping step, and a lot of false bounding boxes are produced.

To enhance the semantic information, the dimension of embedding vector is extended to capture rich features of corner in this paper. Specifically, as shown in Fig. 3, the embedding vector is generated by applying the following operations to the filtered feature map of corner pooling module: 3 × 3 convolution, batch normalization, ReLU and 1 × 1 convolution.In this way,the embedding vector dimension is extended from 1 to 5(Fig.3),which is learned automatically by training data and more powerful in capturing rich semantic information specific to the object.

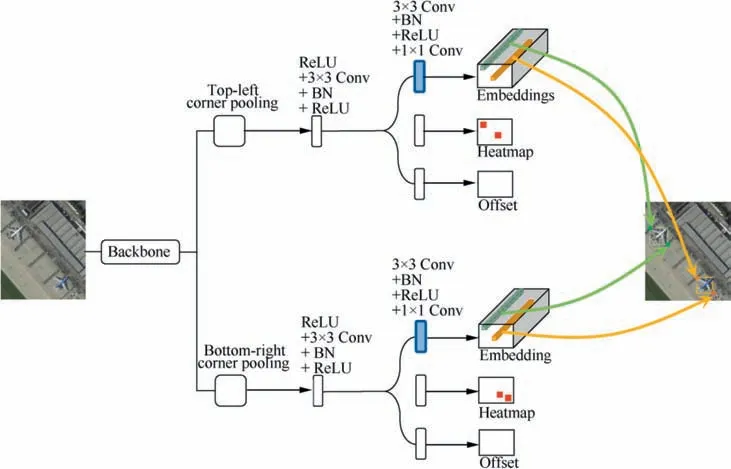
Fig. 3 Multi-dimension embedding vector generation.

2.3. Corner grouping network

Considering the limitations of naive grouping rule in Corner-Net, corner grouping network is presented in this paper to implicitly learn the hidden grouping strategy. As illustrated in Fig. 4, the inputs of corner grouping network are the concatenation of multi-dimension embedding vectors at the topleft and bottom-right corner, and the output is a binary value to denote the grouping degree which is used for computing the grouping loss.Corner grouping network consists of three fullyconnected layers, and the node numbers of hidden layers are 20, 20, and 10 respectively. Driven by the Mean Square Error(MSE) loss function and the back-propagation mechanism,corner grouping network is learned progressively.

2.4. Dynamic random sample choosing for loss computation

The balance between positive training samples and negative ones needs to be considered carefully. In detail, if there are N objects in an image, N top-left corners and N bottomright corners should be grouped, and other N（N-1） corners are not grouped.It can be informed from Eq.(1)and Eq.(2)

Fig. 4 Corner grouping network.

To prevent the trained corner grouping network being biased towards negative samples, the following three sample choosing strategies are considered in this paper:

Definition 1. Sample Choosing Strategy Based on Nearest Neighbor on Embedding (SNNE). SNNE selects the nearest inter-object heatmap corners as negative samples, where the nearest neighbor is measured by the Euclidean distance between embeddings.

Definition 2. Sample Choosing Strategy Based on Nearest Neighbor on Corner Distance (SNNCD). SNNCD selects the nearest inter-object heatmap corners as negative samples,where the nearest neighbor is measured by the distance between corner locations.

The above two strategies aim at choosing hard negative samples.Intuitively,they are powerful in capturing discriminative information for feature learning. However, it is found by experiments that they are suboptimal and unstable.The underlying reason lies in the fact that the whole feature learning procedure is a progressive routine,and pure hard negative samples will significantly impact the back-propagation.For this reason,the following dynamic random sample selection strategy is proposed.

Definition 3. Sample Choosing Strategy Based on Dynamic Random (SDR). SDR randomly selects inter-object heatmap corners as negative samples and dynamically updates chosen samples at each iteration.

Compared to SNNE and SNNCD,negative samples chosen by SDR are more diverse. Specifically, hard negative samples and easy negative samples are chosen in an equal probability.Easy negative samples are conducive to making the backpropagation procedure stable, and hard negative samples help improve discrimination between positive samples and negative samples. Detailed comparisons will be discussed in Section 3.3.3.

2.5. Grouping loss function

To optimize the training loss, Adamoptimizer with the learning rate of 0.00025 is used:

3. Experiments

3.1. Experiment settings

The experiments were conducted on two authoritative datasets: UCAS-AOD and NWPU VHR-10. UCAS-AOD datasetis customized for aircraft and vehicle detection. The size of each image is about 1280 × 685 pixels. In this paper,900 annotated images are used for training,300 images for validation,and others for the test.The NWPU VHR-10,abbreviated to NWPU, is another widely-used object detection dataset,which contains ten classes of objects,namely,airplane,ship, storage tank, baseball diamond, tennis court, basketball court, ground track field, harbor, bridge, and vehicle, respectively called as AA, SP, ST, BB, TC, BC, GTF, HB, BD,and VH. For this dataset, 500 and 100 images are used for training and validation, and the rest 50 images for the test.

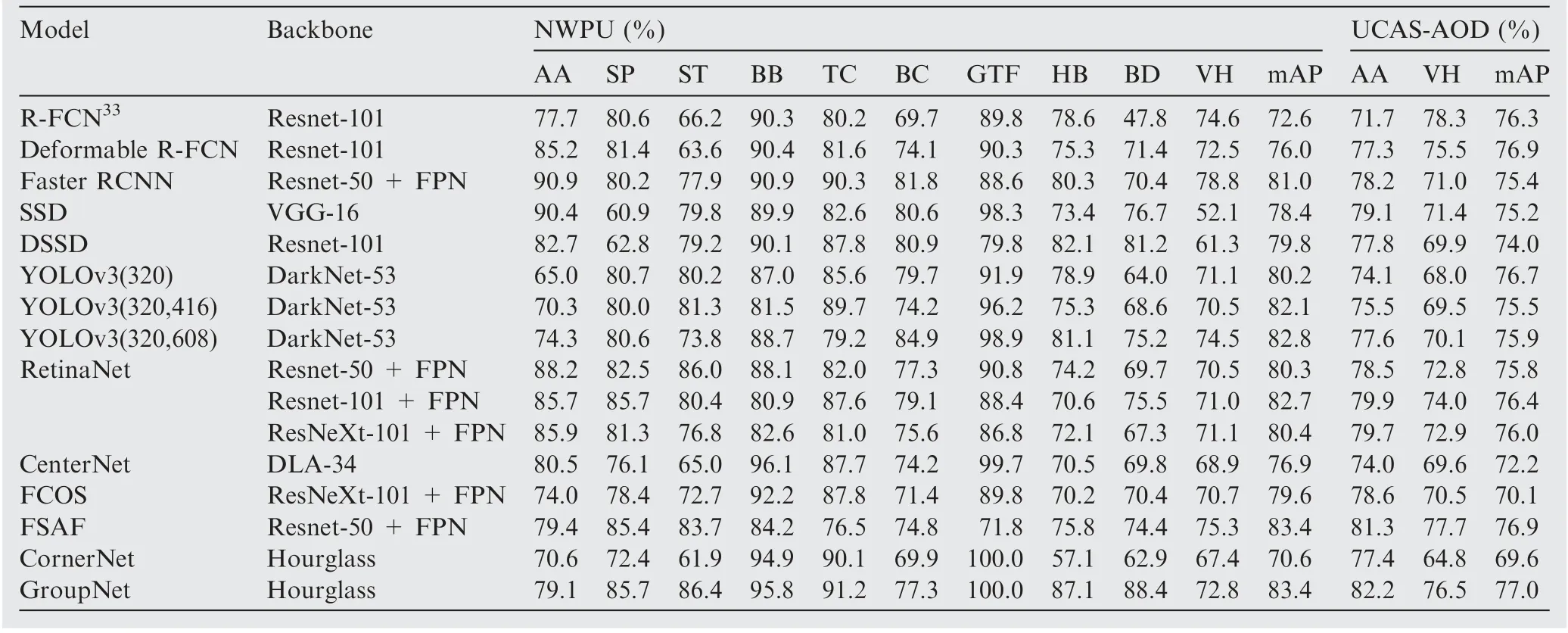
Table 1 Performance comparison of different approaches in terms of AP@0.5.

For a fair comparison,all experiments are conducted within MMDetectionon two 12 GB NVIDIA 2080 GPUs with default parameters. During testing, the top 100 top-left and top 100 bottom-right corners are picked from the heatmap.Groupings that contain corners from different categories are rejected. Then, soft non-maximal suppression (soft-NMS)is applied to suppress redundant detections.

3.2. Experiment analysis

The performance of different approaches on dataset UCASAOD and NWPU are listed in Table 1, where Mean Average Precision(mAP)at IoU thresholds 0.5,i.e.AP@0.5,is used for performance measure. It could be conclusively found from Table 1 that the proposed GroupNet significantly outperforms CornerNet and other approaches. Specifically, GroupNet obtained the best performance in terms of AP over airplane,ship, storage tank, baseball diamond, tennis court, basketball court, harbor, bridge, and vehicle, and gained 8.5%, 13.3%,24.5%, 0.9%, 0.9%, 7.4%, 30%, 25.5%, and 5.4% improvements over CornerNet respectively. The average improvement of AP@0.5 is 12.9%.From the above improvements,it can be seen that the lower the AP taken by CornerNet, the more the improvement gained by GroupNet. In other words, the top four classes with respect to performance improvements are harbor, bridge, storage, and ship, which are stripe-shaped or densely distributed and are difficult to locate by CornerNet.The above comparisons demonstrate the advantages of GroupNet over CornerNet in grouping corner.

Fig. 5 Original image and results comparison on image a, b, c, d, e of method SSD, YOLOv3, RetinaNet, FCOS, FSAF, CornerNet,GroupNet.

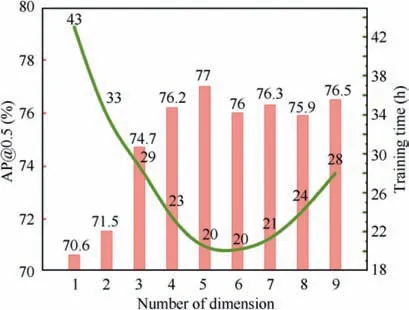
Fig. 6 Performance variation with embedding dimension ranging from 1 to 9 on NWPU.

The advantages of our GroupNet can also be validated by visual comparison. In Fig. 5, images in each column denotes results by different methods on NWPU dataset. From top to bottom, images are arranged by the following order, original image and results comparison of method SSD,YOLOv3,RetinaNet, FCOS, FSAF, CornerNet, GroupNet. It has been demonstrated that,by multi-dimension embedding and corner aggregation learning,GroupNet avoids four aspects on grouping: superfluous bounding box, incorrect location, bad regression, and missed bounding boxes, respectively compared to RetinaNet in Fig. 5 (b), 5 (e), SSD in Fig. 5 (b), 5 (c), 5 (d),FCOS and FSAF in Fig. 5 (e), CornerNet and YOLOv3 in Fig. 5 (a), 5 (c). Gaining an advantage over the anchorbased approaches (such as SSD, YOLOv3, RetinaNet, and R-FCN) and anchor-free approaches (such as FCOS and FSAF) shows great potentials of the keypoints-based method.

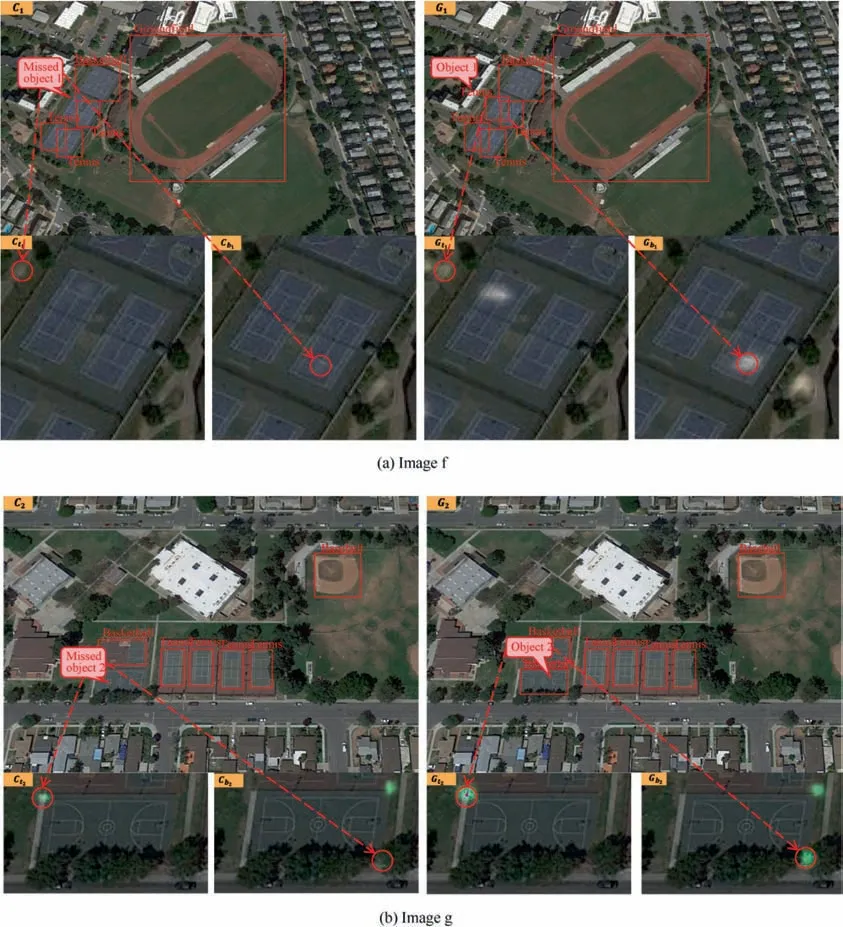
Fig. 7 Results comparison on image f, g.

3.3. Ablation experiment

3.3.1. Performance variation with embedding vector dimension

The performance with dimensions of embedding ranging from 1 to 9 on UCAS-AOD and NWPU is shown in Fig. 6. The height of the bar indicates the performance of AP@0.5, and the value on the line indicates corresponding training time. It can be noted that, when the dimension is less than 6, the performance is trending up and the training time is trending down.The reason is that the corner grouping network obtains more semantic knowledge about grouping by increasing dimension of embedding. The incremental knowledge inspires the corner grouping network heuristically to accelerate the convergence, whose contribution is greater than the computation expense of multi-dimension embedding. In detail,AP@0.5 is increased from 70.6% to 77% on NWPU.

When the dimension is more than or equal to 6,the performance drops slightly from the top and the training time begins to increase. The reason is that too high dimension of the embedding vector exceeds the capacity of corner grouping network,which makes the network difficult to fit.Simultaneously,in order to fit these high embedding vectors,more training time is needed. In consequence, setting the embedding vector dimension to 5 is the optimal choice.

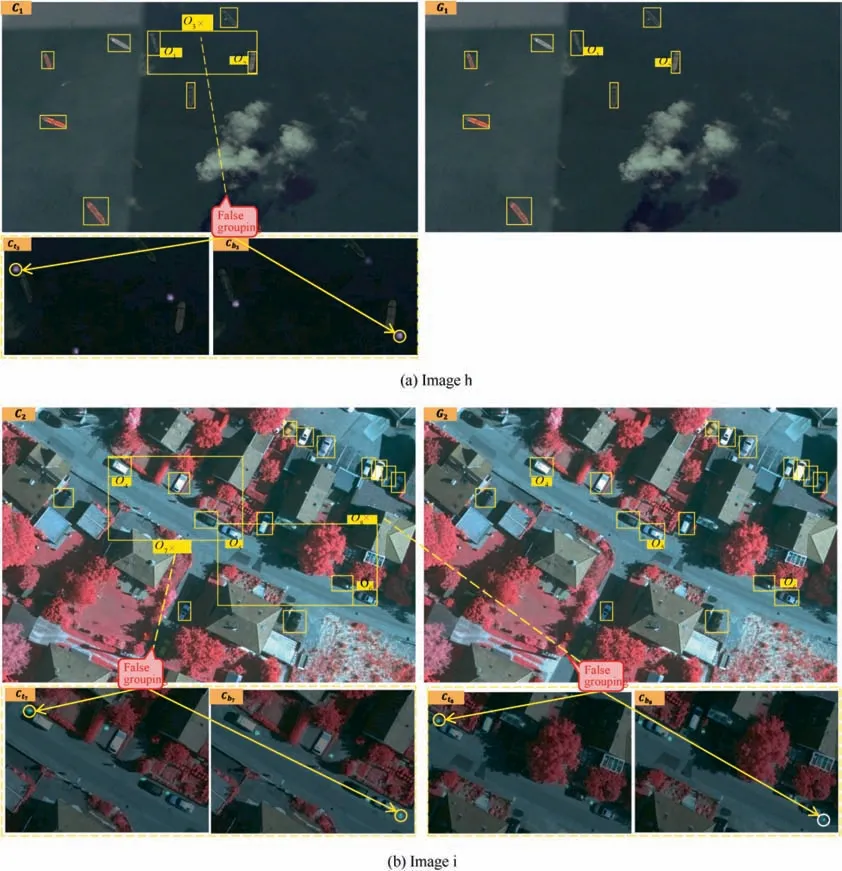
Fig. 8 Results comparison on image h, i.

Table 2 Ablation study on corner grouping network rule on dataset UCAS-AOD and NWPU in terms of AP@0.5, AP@0.75, AP@0.5:0.95, ARS, ARM and ARL.

Table 3 Grouping performance comparison in real cases.

It can be observed from Fig.7 that corner features of CornerNet with one-dimension embedding are weaker than those of GroupNet with multi-dimension embedding,which leads to the absence of the bounding boxes in CornerNet.Tennis court in image Cand basketball field in image Cin CornerNet are missed due to the obviously weak feature shown in the underneath heatmap,which hinders CornerNet from reliable grouping corner. In other words, the limited information carried by one-dimension embedding impacts the grouping confidence in corner aggregation.

3.3.2. Corner grouping rule

The most important differences between GroupNet and CornerNet lie in embedding vector dimension and corner grouping rule. To understand how these two factors work, CornerNet,GroupNet and its variant, GroupNet_1 are used for the following ablation experiment. GroupNet_1 learns to group corner on one-dimension embedding vector. That is to say, the difference between CornerNet and GroupNet_1 is the corner grouping rule, and the difference between GroupNet_1 and GroupNet lies in the dimension of embedding vector under the premise of corner grouping.

From the false samples of CornerNet,it can be inferred that the main difficulty in the corner aggregation is the low interobject distance and high intra-object distance. Specifically,the distances Dof false samples O，O，Oare 0.0635,0.3543,0.1092,which are even lower than that of positive samples,e.g.,0.0640 in O,and 0.2384 in O.It is difficult to separate the correct aggregations from the false ones with a fixed threshold on one-dimension embedding vector space. However, in our GroupNet, the low inter-object distance and high intra-object distance are tuned and driven by corner group learning on multi-dimension embedding. From the output D,thetop-leftandbottom-rightcornersof O，O，O，O，Oare to be grouped,which are consistent with the ground-truth labels. From the above comparisons, it can be found that not only grouping network learning but also multi-dimension embedding designed by our GroupNet are beneficial for corner aggregation.

3.3.3. Dynamic random sample choosing strategy

Sample choosing strategy is closely related to the corner grouping performance and the final performance. To investigate the role of dynamic random sample selecting strategy in corner grouping, the other two sample choosing strategies are compared to the dynamic random sample choosing strategy presented in this paper.

It can be deduced from Table 4 that SDR strategy reaches a better trade-off than the other three strategies in terms of AP and time consumption. Specifically, there are two factors that help GroupNet outperform other strategies including Corner-Net.On the one hand,at each training iteration,the number of negative samples is equal to the number of positive samples,which helps to reduce the bias towards the negative samples.On the other hand, SNNE preferentially groups the objects

Fig. 8 (a), (b) show the visual comparison of CornerNet and GroupNet on corner grouping.Due to the impacts caused by naive corner aggregation, CornerNet generates many false bounding-boxes. It could be seen from corner heatmaps of CornerNet,as shown in the bottom part of Fig.8(a),8(b),that the bounding box of Ois wrongly aggregated with the top-left corner of Oand the bottom-right corner of Oin Fig. 8 (a).Similarly, the bounding box of O，Oare wrongly aggregated with the top-left corners of O，Oand the bottom-right corners of O，Oin Fig.8(b).As shown in line 2 of Table 2,with the help of grouping network learning, AP@0.5 from Corner-Net to GroupNet_1 is increased by 1.0%and 1.8%on UCASAOD and NWPU.As shown in line 3 of Table 2,when multidimension embedding and grouping network learning are adopted simultaneously, AP@0.5 from CornerNet to Group-Net is further increased by 7.4% and 12.8% on UCAS-AOD and NWPU, where the dimension of each corner embedding vector is 5. Besides, we also evaluate the Average Recall(AR) on small, medium, and large objects (AR, ARand AR) follwing the definition in Ref. [13]. [·] indicates the performance improvement.of the nearest embedding, and SNNCD preferentially groups the objects of the nearest position, while the dynamic random samples chosen by SDR cover the above two types simultaneously.

Table 4 Ablation experiment of sample choosing method on NWPU.

4. Conclusions

In this paper, a simple yet effective corner grouping network,namely GroupNet,is proposed to solve the corner aggregation problem inherent in the CornerNet. The relationship between the top-left corner and the bottom-right corner is enriched by a multi-dimension embedding, and the end-to-end corner grouping network is more robust to reduce the ambiguity caused by naive corner aggregation rule. Experiments on two widely-used datasets demonstrate the effectiveness and strength of the proposed approach. Future work will focus on the performance enhancement of anchor-free detectors by generative adversarial learning.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgment

This research was supported by Natural Science Foundation of China (No. 62071466).