Factor graph based navigation and positioning for control system design: A review

Xiwei WU, Bing XIAO, Cihang WU, Yiming GUO, Lingwei LI

School of Automation, Northwestern Polytechnical University, Xi’an 710072, China

KEYWORDS Factor graph;Navigation;Optimization methods;Positioning;Sensor modeling

Abstract Navigation and positioning is an important and challenging problem in many control engineering applications.It provides feedback information to design controllers for systems.In this paper,a bibliographical review on factor graph based navigation and positioning is presented.More specifically, the sensor modeling, the factor graph optimization methods, and the topology factor based cooperative localization are reviewed. The navigation and positioning methods via factor graph are considered and classified. Focuses in the current research of factor graph based navigation and positioning are also discussed with emphasis on its practical application.The limitations of the existing methods,some solutions for future techniques,and recommendations are finally given.©2021 Chinese Society of Aeronautics and Astronautics.Production and hosting by Elsevier Ltd.This is an open access article under the CC BY-NC-ND license(http://creativecommons.org/licenses/by-nc-nd/4.0/).

1. Introduction

Space and marine exploration are extensively supported by the USA, Europe, China, etc. The increase in the diversity and complexity of missions has motivated significant requirements for fast and accurate navigation, positioning, and timing services.However,the unified solution for the current navigation system is to fuse information gained from multiple sources including Global Positioning System (GPS), Inertial Navigation System (INS), and magnetometer. It is characterized by the following three drawbacks:

(1) It is difficult to satisfy the accuracy and reliability requirements in complex application scenarios. The traditional single source navigation methods are inefficient.The traditional integrated navigation system is only limited to optimize specific sensors and measurement sources. Those navigation methods are not adaptive and accurate. Moreover, when the GPS signal is interfered and blocked, the reliability of navigation cannot be guaranteed.

(2) Great challenges are posed for the current state estimation method when they are applied to small unmanned systems. Although many methods have been proposed to estimate the navigation states,ranging from linear filtering to nonlinear filtering, from Kalman filtering to Extended Kalman Filtering (EKF), and to the current Particle Filtering(PF),predictive filtering,etc.However,due to the miniaturization and cluster development of unmanned systems, nonlinear and non-Gaussian problems of the navigation system are becoming serious.This leads to the fact that the traditional filtering methods cannot satisfy the high precision requirements of the navigation system. Moreover, the traditional nonlinear filtering methods are often accompanied by a series of problems such as expensive computation, which causes unaffordable calculation cost to the current unmanned system computers.

(3) The current navigation system suffers from asynchronous, multi-rate or even variable-rate problems of the sensor data.The navigation system is generally composed of heterogeneous sensors. Due to the influence of each sensor and the working environment, asynchronous, multi-rate or even variable-rate phenomena occur in the sensor data transmission.Traditional methods utilize outer shove and interpolation, and curve fitting methods to align data. However, high alignment accuracy cannot be guaranteed by these methods when considering asynchronous, multi-rate and variable-rate phenomena. The combination mode of sensors is also related to the operating environment and tasks. Consequently, the traditional data alignment methods are hard to achieve desirable performance in different operating situations due to the lack of adaptive ability.

To solve the above problems, an advanced concept called All-Source Positioning and Navigation(ASPN)was proposed by the Defense Advanced Research Projects Agency(DARPA)in November 2010.In this framework,multiple available information resources were integrated to compensate for the drawbacks of individual parts and outperform the single navigation system. Its goal is to develop a highly autonomous, highprecision,robust,and plug-and-play unified navigation framework.It ensures that continually varying mission requirements and environment conditions can be adaptively satisfied on any platform like aircraft, spacecraft, and ship. The main features of the ASPN system are rapid integration, reconfiguration,abstraction and filtering algorithm of any combination of navigation methods.

Some ASPN solutions have been proposed.However,only specific problems have been addressed. In Ref., a software abstract method was developed to realize plug and play of sensor.In Ref.,the critical technologies of ASPN were analyzed and predicted. Space-based all-source navigation technology was studied in Ref.. However, the aforementioned ASPN schemes can only provide the basic concept and the general framework. Their practical implementation becomes a challenging problem. Recently, the factor graph based method has attracted numerous research attention due to their unique advantages.It is featured by plug and play and its great capability of handling the nonlinear problem in navigation system and the asynchronous problem in data transmission process. The first attempts to realize ASPN algorithms were reported by Georgia Institute of Technology. Using the factor graph method,they encoded sensor measurements with different frequencies,delays,and noise distributions.It provided a flexible foundation for plug-and-play navigation and can integrate new evolving sensors freely.If a sensor becomes unavailable due to signal loss or sensor fault, the system simply refrains from adding the associated factors,and no special procedure or coordination is required. Up to now, the factor graph based navigation and positioning is still a hot issue because of its great application potentials.

1.1. Motivation and contribution of this review

Several survey papers and books on the factor graph design methodologies were seen prior to 2017.However, to the author’s best knowledge,there is few literature in investigating the factor graph based navigation and localization methods.A comprehensive survey is highly demanded to review the large variety of factor graph based navigation and positioning systems. Motivated by this, this paper is aimed at providing a comprehensive review on the recent development of factor graph based navigation and localization techniques. An overview of the state of the art and unsolved problems in the areas of factor graph based navigation and localization are provided.

1.2. Organization of this paper

The remainder of this paper is organized as follows. An overview of the factor graph is presented in Section 2, and the recent developments in factor graph based navigation techniques are surveyed in Section 3.The factor graph based localization techniques are discussed in Section 4. In Section 5, a brief review is made about the implementation of factor graph based navigation and localization.Discussion and conclusions are given in Section 6.

2. Factor graph

In general, multi-variable global functions are often decomposed into the product of multiple local functions. Each local function depends on a subset of variables.This decomposition can be represented by a bipartite graph, called factor graph.The transfer relationship between system states was intuitively represented via factor graph.Currently, factor graph is widely used in the optimal control and motion planning,the filtering and smoothing,the model-based signal processing,the message passing,the artificial intelligence,the decoding and coding,the classification,the electric network,etc.

2.1. Definition

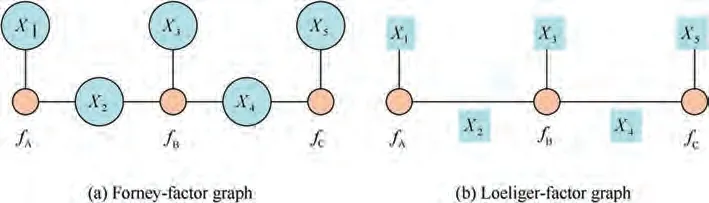
Fig. 1 Expression form of factor graph.

There are two common ways to design factor graph.One is the factor graph proposed by Forney and the other is developed by Loeliger.They have the same essence. Both can represent the factorization of multivariate functions. The only difference is the representation of symbols,as shown in Figs.1(a) and (b). The Forney-factor graph supports hierarchical modeling and is compatible with standard block diagrams,while the Loeliger-factor graph is convenient to convert to a probability model.Note that the Loeliger-factor graph is common in navigation and localization applications.

2.2. Markov property

2.3. Matrix form of factor graph

Suppose that the state xat time k+1 is predicted by the state xat time k through the function h（·）, i.e.,

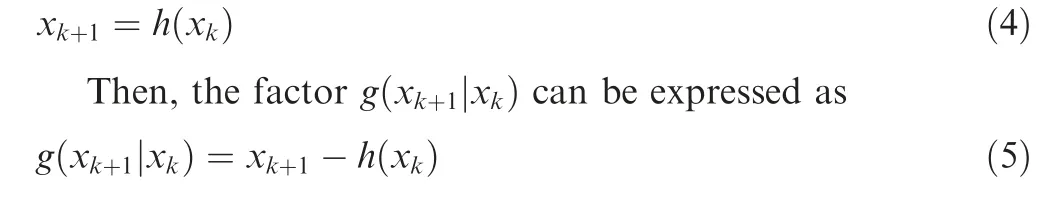
The derivative of a factor graph is a matrix formed by the derivation of each factor for each variable. Each row of the matrix represents a factor, and each column represents a variable.The Jacobian matrix of the factor graph reflects the structure of the factor graph. The Jacobian matrix of the factor graph is also called the matrix form of the factor graph.A typ-

ical factor graph and the corresponding Jacobian matrix are shown in Fig. 2, ^xis the estimate of the state x, and J（^x）is the Jacobian matrix.

2.4. Sum-product algorithm

In a factor graph, the process from variable nodes to factor nodes or from factor nodes to variable nodes is through information interaction.The sum-product algorithmis a messagepassing algorithm based on factor graph.The algorithm firstly converts directed graphs and undirected graphs into factor graph, and finally derives and solves them based on the factor graph.

Let μ（x ）denote the message sent from the node x to the node f in the operation of sum-product algorithm, and n（v ）denote the set of neighbors of a given node v in a factor graph.Σis the ‘‘not-sum” or summary indicating the variables being summed over. The message computations performed by the sum-product algorithm may be expressed as follows:

Variable to local function:

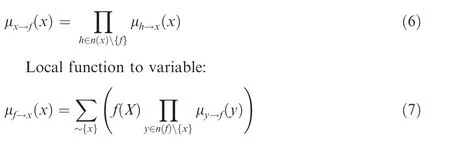
where X=n （f ） is the set of arguments of the function f, and h ∈n（x ）｛f ｝ denote the set of elements that belong to n（x ）but not to f.

The essence of factor graph and the sum-product algorithm is that the information that passed from the factor node along the variable node is the product of factor, the information passed along all the variables except this variable, and then we sum all the other related variables except the variable.The message passing algorithm based on factor graph is efficient for finding the marginal probability distribution of variables.

3. Factor graph based navigation

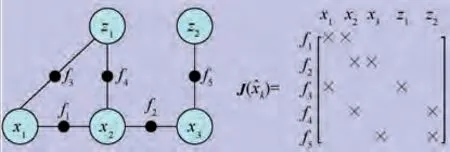
Fig. 2 Factor graph and corresponding Jacobian matrix.

Since factor graph techniques have been well-developed, they can be adopted for sensors fusion. This has attracted lots of attention and improves the performance over the existing filtering methods. The existing optimization approaches for factor graph based navigation are listed in Table 1.

Several survey papers have been seen on factor graph based navigation methods. A factor graph based Bayesian Kalman filtering method was designed to ensure the optimal performance of the posterior distribution of unknown noise parameters in Ref.. This method was applied to solve the positioning and tracking problem.In Refs., a factor graph based probability model was designed to provide a better solution for nonlinear optimal navigation problems. In Ref., a three-view constraint collaborative navigation algorithm based on factor graph was proposed.The method is used to compute cross-covariance terms on demand, and solve the distributed navigation. In Ref., a navigation solution by using nonlinear optimization was designed through processing internal measurement data from Inertial Measurement Units(IMU) and any other available sensor. This method is based on the incremental smoothing algorithm, which can automatically determine the number of states to be recomputed at each step, effectively acting as an adaptive fixed-lag smoothing.More recently, a novel approach of high-rate information fusion for inertial navigation systems was proposed.The pre-integration technology via the IMU introduces an equivalent IMU factor. This thereby greatly reduces the number of states that must be added to the navigation system. In Ref., an incremental constrained smoothing framework was presented.

To solve the problem of poor real-time performance for integrated navigation, an efficient incremental inference algorithm over the factor graph is applied,whose performance approaches the solution that would be obtained by a computationally-expensive batch optimization at a fraction of the computational cost.In Refs.,a sliding window factor graph was designed to extend the existing incremental smoothing method.It provides a low-latency solution while estimating the fully nonlinear navigation state. A novel multi-modal Gaussian mixture model was established to adapt to the error distribution of the sensor fusion.Combining Expectation Maximization (EM) with nonlinear least squares optimization can obtain a solution with good convergence and high computational efficiency.

The factor graph methods have also been applied in the aerospace engineering. To satisfy the higher requirements for sensor accuracy of micro air vehicles,a graphics fusion method was presented in Ref.. It can estimate the best performance of all sensors in a smoother and compatible mode. In Ref.,a factor graph based method was designed to model and implement the multi-satellite relative state estimation. The factor graph shows the joint probability distribution of the entire state and the measurement history of all participating satellites. In Ref., a single-satellite positioning algorithm via thesynergy factor graph was proposed. In Ref., a factor graph approach for attitude estimation of spacecraft using a gyroscope was developed. It utilizes a factor graph method via the sliding window to deal with measurement delay.

Table 1 Existing optimization methodologies for factor graph based navigation.

3.1. Factor graph based navigation framework

The factor graph based navigation framework consists of three parts.The first part is system modeling including prior model,state model, and measurement model, but mainly in sensor measurement modeling. Then, an optimal sensor selection mechanism is developed to select the best sensor combination for navigation. The last part is to design joint optimization algorithm for state estimation of navigation system.A detailed flow of the existing factor graph based navigation schemes is shown in Fig. 3.

The joint density function of state estimation can be denoted by factor graph. As shown in Fig. 4, the state variables of system are represented as variable nodes of the factor graph and the prior information. The state transition and the measurement process for state estimation are denoted as the factor node of factor graph.The factor graph framework could more intuitively reflect the dynamic variation process of the state estimation and sensor measurement for the navigation system.

The state and measurement equation are factorized based on the Gaussian distribution.The ultimate goal of the navigation system is to calculate the Maximum Likelihood Estimation (MLE) using the nonlinear least square given by

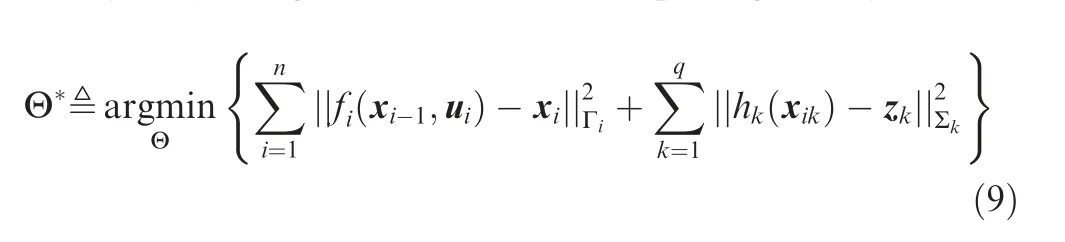
where Θ is navigation state, and Γand Σdenote the covariance matrix of the process noise and the measurement noise,respectively.

3.2. Measurement modeling

For the Gaussian noise model, the measurement factor in accordance with any sensor S is

Fig. 3 Factor graph based navigation scheme.

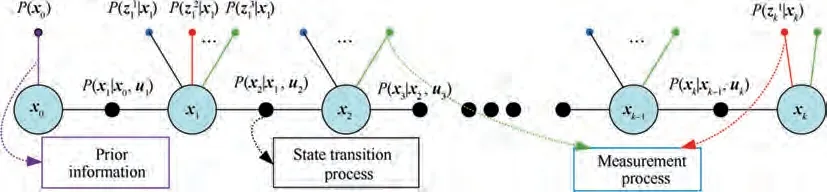
Fig. 4 Factor graph representation of joint probability density function.

3.2.2. Binary factor

The binary factor is related to the state of two adjacent moments. It describes the measurement between the states.The time update of the navigation state x can be expressed as

3.2.3. Multiple factor

It is related to the state of multiple moments,called the multiple factor. The modeling method is similar to the unary and binary measurement factor.

That plant is a foreigner, no doubt, said the thistles and theburdocks. We can never conduct ourselves like that in thiscountry. And the black forest snails15 actually spat16 at the flower.Then came the swineherd; he was collecting thistles and shrubsto burn them for the ashes. He pulled up the wonderful plant, rootsand all, and placed it in his bundle. This will be as useful as any, he said; so the plant was carried away.

Using the above modeling methods, IMU, GPS, magnetometer, altimeter, and other sensors can establish a complete factor graph model.

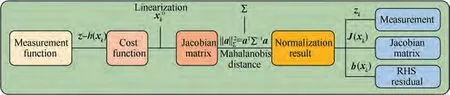
Fig. 5 Flowchart of sensor modeling.

3.3. Sensor selection

To ensure navigation accuracy and satisfy resource constraints, it is necessary to select the optimal subset of sensors to estimate the state of the navigation system.To solve the global self-localization of multi-sensor mobile robots, a robot positioning sensor selection algorithm using the informationtheoretic model selection criteria was proposed.The algorithm is based on Bayesian filtering probabilistic inference,and estimates the uncertainty of sensor measurement and sensor validity during robot localization.In Ref.,a convex optimization based Heuristic algorithm was presented to approximately solve the sensor selection.Focusing on the sensor selection in resource-constrained sensor networks,a greedy sensor selection algorithm was established in Ref.. This transforms the problem of sensor selection into the maximization of the sub-module function on a uniform matroid.

Since factor graph based navigation approaches have been well-developed, the sensor selection strategies related to these methods have been investigated. In Ref., a novel constrained optimization selection mechanism was designed to identify the optimal subset of active sensors during the initialization process and when any sensor condition changed. A subset of sensor candidates via the heuristic rules was constructed. The proposed approach can quickly determine candidate subsets by maximizing the observable coverage of state variables. In Ref., a sensor selection and optimization method based on factor graph was presented. The original measurement values and characteristics of the sensors are considered to estimate and select sensors. To address the sensor deviation and noise model updating in the factor graph framework during the fusion process, a sensor optimization approach was proposed through consistency checking.Those methods integrating with factor graph provide a multi-sensor fusion framework. It encodes sensor measurements with different frequencies, time delays, and noise distributions, and can satisfy the requirements of environmental adaptation in multi-sensor fusion.

3.4. Factor graph optimization

There are currently a large number of researches on the optimization algorithm design of factor graph.In Ref.,the application of factor graph in the modeling and solving of largescale robot inference problems was presented.

In the process of factor graph optimization,given the initial estimate ^Xof the state Xfor navigation system, solving the update increment Δ of the state Xcan be transformed into the standard linear least squares solution of Δ, i.e.,

3.4.1. Gauss-Newton optimization algorithm

The calculation equation of the Gauss-Newton optimization algorithm is

Subsequently, we can update the residual e for iteration.

The Gauss-Newton optimization algorithm omits the calculation of second-order Hessian matrix.The amount of computation is reduced. However, JJ may be singular (irreversible)or ill-conditioned. The equation will have no solution. Poor stability will be led and the algorithm will not converge.

3.4.3. SAM optimization algorithm

In Ref., the square root SAM approach was developed by decomposing the correlation information matrix or the measurement Jacobian matrix into the square root form. This approach has several significant advantages over EKF. It can be used in either batch or incremental mode. Moreover,this method has better capability of dealing with non-linear process and measurement models.

To address the problem of multi-robot distributed Simultaneous Localization and Mapping (SLAM), the number of algorithms for decentralized data fusion considerably increases. In Ref., an extended SAM method was presented to achieve Decentralized Data Fusion-Smoothing and Mapping(DDF-SAM).This method is effective in computing cost,communication bandwidth, and node failure. It enhances the SAM graphical model approach by introducing constraint factor graph as an extended model. It can extend the network topology scalable to large robot network.Subsequently,a consistent decentralized data fusion method for robust multirobot SLAM in dangerous and unknown environments was proposed,namely DDF-SAM 2.0.It merges local and neighboring information into a consistent enhanced local map,instead of using the traditional method of avoiding repeated counting of information in the previous DDF-SAM algorithm.

The SAM algorithm is to describe the SLAM problem as a least square.This method utilizes the solver QR or Cholesky to smoothly decompose matrix. We rewrite Eq. (18) to||Aθ-b||, and then

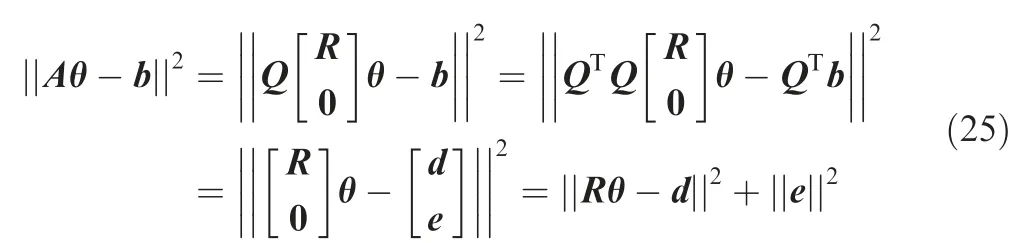
Define ［d，e ］=Qb,d ∈R,e ∈R,and then if and only if RΔ=d,Eq.(25)is the minimum,i.e.,||e||is the residual of the least square solution. Therefore, the QR decomposition simplifies the least square problem to solve linear equations with unique solutions

where Δis the updated increment of all state variables.

The number of factor nodes and variable nodes for the integrated navigation system via factor graph are increasing by the system running time.This causes the amounts of computation to increase. The batch processing method may not guarantee the real-time performance of the navigation system.

3.4.4. iSAM optimization algorithm

To solve the shortcomings of batch processing, a novel approach using fast incremental matrix factorization for SLAM was proposed, called iSAM.And iSAM provides an efficient and accurate solution by updating the QR decomposition of the naturally sparse smoothing information matrix so that only those matrix entries that actually change are recalculated. In Ref., the possibility of effective incremental online estimation of sparse factor graph under non-Gaussian conditions was considered.The method of popularizing iSAM and robust incremental least-squares estimation was designed to remove the assumption of Gaussian factor.It thereby significantly expands the application range of these algorithms.

When a new measurement arrives, the iSAM method utilizes QR-updating to directly modify the previous decomposition more efficiently, instead of updating and reconstructing matrix A, adding a new measurement row wand RHS γ to the current factor R. The new system generated by RHS dalso is not the correct form of factorization.

By expanding the factor R to an appropriate number of empty columns and rows, new variables are added to the QR factorization. This expansion is only done before adding new measurement rows containing new variables.At the same time,RHS dadds the same number of zeros.

iSAM updates the square root information matrix R by using a new measurement increment.The update is performed by Givens rotation. It usually only affects a small part of the matrix. Hence, less computing cost is led than the batch decomposition.However,due to the addition of new variables,the variable ordering is far from optimal.iSAM performs periodic batch processing steps, in which variables are reordered,and batch decomposition is required. Since linearization is only performed in batch processing steps, and the frequency of periodic batch processing steps is heuristically determined,the solution is not optimal.

3.4.5. iSAM2 optimization algorithm

In Ref.,a new data structure,namely the Bayes tree structure was presented. It provides an algorithm basis to better understand the existing graphical model inference algorithm and its connection with the sparse matrix factorization,and more naturally maps to the square root information matrix of the SLAM problem. Based on the Bayes tree structure, a novel incremental sparse matrix factorization method was proposed.It is called iSAM2. The algorithm transforms the matrix update into a simple editing operation of the Bayes tree and its conditional density. A new method of incrementally changing the order of variables was proposed, which is more efficient in computation. The efficiency and accuracy of the proposed algorithm are based on smoothing relinearization.To implement this technique, the following six procedures are usually essential,and their correlation is shown in Fig.6.

Algorithm 1.Eliminate variables.The elimination algorithm converts the factor graph into a Bayes net. The method is to eliminate one variable at a time and transform it into a node of the Bayes net that is gradually established.After eliminating all variables,the Bayes net density is defined by the product of the conditions generated at each step.

Algorithm 2. Create Bayes tree. A new data structure is introduced to better characterize the equivalence of linear algebra. Since the Bayes net obtained by elimination/factorization is chord, it can be transformed into a tree-shaped graphical model, making the process of optimization and marginalization easier.

Algorithm 3.Update Bayes tree.After the Bayes tree is created, incremental information will be stored in the form of a Bayes tree, and the square root information matrix will be computed. Convert the affected part of the Bayes tree into a factor graph,add new factors to it,utilize the new elimination ordering to form a new Bayes tree, and reconnect the unaffected subtrees.

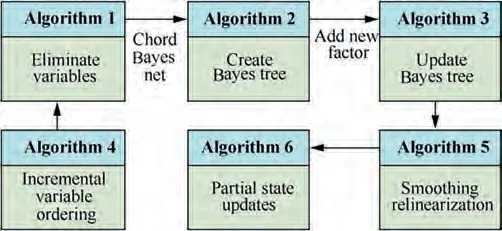
Fig. 6 Correlation diagram of iSAM2 algorithm.

Algorithm 4. Incremental variable ordering. The column approximate minimum degree algorithm is utilized to reorder the Jacobian matrix, the row and column factors of the reordered Jacobian matrix are remapped to the factor graph, and subsequently the elimination variables algorithm is executed.When performing incremental inference in the Bayes tree,variables can be reordered each incremental update,thereby avoiding periodic batch reordering.

Algorithm 5.Smoothing relinearization.After executing the incremental variable ordering algorithm, there are still some variable nodes that are not linearized,and the fluid relinearization technique is designed for linearization. To re-linearize the selected variable, all related information should be removed from the Bayes tree and replaced by the corresponding original nonlinear factor. The re-eliminated small groups must also consider the edge factors that pass from the subtrees.

Algorithm 6. Partial state update. Starting from the root until all leaf nodes are completely reversed, the incremental vector used to update the linearization point is obtained. The partial state update starts by solving all the variables contained at the top of modified tree.A threshold is set for the incremental vector,and the linearization point is updated only when the threshold is reached, which can save computation cost.

The iSAM2 algorithm has three prominent advantages.Firstly,Bayes trees provide a better understanding of the probability density for matrix factorization. Secondly, the algorithm shows how the fairly abstract update to a matrix factorization translates to a simple editing of Bayes tree and its conditional density.Thirdly, a new sparse non-linear incremental optimization algorithm is obtained by using Bayes trees. The algorithm utilizes incremental variable to reorder and smooth relinearization without periodic batch processing steps. This improves computational efficiency and accuracy.

4. Factor graph based localization

The factor graph is not only utilized in the field of navigation,but also widely applied in positioning. A list of the existing investigation on factor graph based localization methods is provided in Table 2.

4.1. Factor graph based SLAM

The SLAM is mainly divided into two processes:the front-end and the back-end. The front-end processes the sensor data.The back-end mainly optimizes the results of front-end. The back-end optimization is essentially a state estimation prob-lem. Therefore, the state estimation inference algorithm via factor graph has a wide range of applications in the process of specific SLAM back-end optimization. In Ref., the factor graph theory was firstly proposed to solve the SLAM. In Ref.,the robust closed-loop pose graph SLAM was modeled as a Bayes net. It can be solved by the classification EM algorithm.In Ref.,a factor graph based method was proposed to remove various nodes in SLAM graphs. By reducing the size and density of the graph, the proposed method can alleviate some computational challenges when performing inference on long-term pose graphs.In Ref.,a precise and sparse scalable SLAM approach was proposed. The method is not to eliminate variables, but to split the separators that connect the subgraphs. In Ref., a novel approach to effectively decompose multi-factor graph combinations with common estimated variables was designed. The method reuses the variable ordering of the parent graph, and the magnitude difference can be produced in the time required to solve the fusion graph.

Table 2 Classification of different positioning scenarios and methods.

To reduce the computational burden of back-end optimization, a novel method for the pre-integration of contact information through any number of contact switches using hybrid pre-integrated contact factors was developed in Ref.. The proposed hybrid modeling method reduces the number of variables in the nonlinear optimization. It only needs to add new states alongside the camera or selected keyframes. In Ref.,a positioning algorithm based on sliding window factor graph was presented. The proposed method incorporates landmarks from third-party maps into the evaluation and shows how to utilize sliding window to correct data associations. To solve the singular problem caused by the irreversibility of sensor noise covariance matrix, an improved smoothing approach based on Kalman filter was investigated. In Ref., a novel incremental Pose Graph Optimization (PGO) scheme named G-PGO was designed to bypass the Schur complement and consistency of incremental factor graph optimization. GPGO method does not optimize the global absolute pose of robot, but the estimated variable is the relative pose.

Factor graph is also involved in the field of target tracking and detection. In Ref., a novel method of joint tracking and registration was designed to address the problem of multitarget multi-sensor monitoring with sensor bias. The designed joint estimator can retain the real-time function and exhibit decoupling, when all cross-correlation is considered. In Ref., a multi-camera target tracking system via factor graph was established.It aims to estimate the state of moving targets using a message propagation framework. Moreover, to solve the problem of incorrect initial assignment of detection tasks for accurate and reliable tracking of multiple moving objects in three-dimensional space, a new method based on factor graph optimization was proposed in Ref..

The SLAM optimization methods based on factor graph are summarized in Table 3.

4.2. Factor graph based GNSS

The Global Navigation Satellite System (GNSS) has dominated the autonomous navigation. Therefore, many researchers have applied factor graph optimization methods to GNSS. In Ref., a novel approach for online identification and elimination of pseudo-distance measurements was presented. It does not rely on additional sensors, maps, or environmental models, and is more inclined to describe the localization problem as a Bayes inference in factor graph. In Ref., a method that utilizes the fisheye camera to capture skyscape images to further classify Non-Line-Of-Sight(NLOS)and Line-Of-Sight (LOS) measurements was developed. The original INS and GNSS measurements are closely combined using probability factor graph models. In Ref., the localization problem was described as a MAP probability estimate,and it is solved by using graph optimization instead of Bayesian filters. Graph optimization takes advantage of the inherent sparsity of the observation process to satisfy real-time requirements. In Ref., an incremental graph optimization scheme was designed to reduce the convergence time of precise point positioning. The proposed method combines GNSS positioning with incremental graph optimization.

The degradation of GNSS data in urban environments leads to the poor performance of traditional GNSS localization methods such as EKF and PF. The latest developments in sensor fusion methods via factor graph theory are mainly used in robotic applications. However, it can also be applied to GNSS data processing. In Ref., a factor graph based method was proposed.It is combined with several robust optimization techniques to evaluate their applicability in robust GNSS data processing. In Refs.,the pose graph optimization method using GNSS was designed to estimate the precise trajectory of the vehicle.The closed-loop of pose graph is generated by time-relative real-time kinematic GNSS technology.It is a method of using a single low-cost GNSS receiver to implement precise carrier phase time-difference GNSS. In Ref., a factor graph optimization algorithm for cooperative localization via 3D mapping aided GNSS was developed to improve the localization accuracy of dense urban areas. In addition,Ref.utilized EKF and Factor Graph Optimization(FGO) to evaluate loosely-coupled and tightly-coupled integration by using the challenging dataset collected in the urban canyon. Comparison between the performance of EKF and factor graph based GNSS/INS integration was done in Ref..

4.3. Factor graph based cooperative localization

Cooperative localization is an effective means to improve performance such as positioning accuracy and availability.Due to the strong applicability of factor graph, it is also utilized in cooperative localization. In Ref., a joint message passing node localization algorithm based on ranging was proposed.The complexity and high communication cost of the existingwireless network node positioning algorithms based on message passing algorithm were addressed. In Ref., a cooperative localization algorithm was developed, which integrates the Fisher information matrix between adjacent agent nodes to evaluate the ranging performance of the agent node to its adjacent nodes. To address the ranging and positioning error of cooperative nodes,a factor graph assisted distributed cooperative localization algorithm was presented.In Ref., a cooperative localization optimization of robots was presented.

Table 3 Factor graph based SLAM.

In the past two decades, precise wireless geolocation has received widespread attention and is expected to play an important role in current and future wireless communication systems. In Ref., a novel factor graph based geolocation technology was proposed, which utilizes Direction of Arrival(DOA)information to locate a single unknown radio transmitter to improve positioning accuracy. A three-dimensional multi-target geographic location factor graph technology based on the DOA was presented.The proposed factor graph detector only uses the average and variance of the DOA measurement, including the azimuth and elevation angles. In Ref., a unified factor graph based framework was developed to address passive location based on TOA measurement in wireless sensor networks. Based on the linearization of distance measurement, the Forney-factor graph model was constructed, and a corresponding Gaussian message passing algorithm was designed to obtain the target position.To improve geolocation accuracy,a DOA-based tracking algorithm was proposed,which integrates EKF and geolocation into an factor graph framework.The predicted state information obtained from EKF is used not only for filtering, but also for observation, as a prior information of factor graph geolocation.

In addition to the preceding factor graph based geolocation approach, other cooperative localization methods based on factor graph have also been discussed. In Refs., an enhanced RSSD-based factor graph algorithm using weighted least square was presented to effectively reduce the impact of Received Signal Strength Difference (RSSD) measurement variance difference on positioning accuracy.In Ref.,a factor graph based ultra-wideband positioning algorithm based on an improved Turkey robust kernel was proposed. This algorithm not only overcomes the drawbacks of least squares algorithm against non-Gaussian noise in ultra-wideband positioning,but also compensates the shortcomings of Turkey’s robust kernel algorithm. To improve the global positioning accuracy of autonomous underwater vehicle, a cooperative localization algorithm based on factor graph and maximum correntropy was presented in Ref..Meanwhile,a vehicle localization estimation approach based on factor graph was presentedand applied to underwater acoustic cooperative localization.

4.4. Cooperative localization based on topology factor

To address the problem of association uncertainty and coordinate transformation in cooperative localization, the novel methods based on topology factor graph have been investigated. In Refs., an approach based on factor graph for vehicle-infrastructure cooperative localization was presented.The proposed method adds topology factor (distance between vehicles)as a constraint when using the data from internal and external sensors of the vehicle to locate the vehicle.In Ref.,a factor graph based method is proposed to estimate the bias in sensor measurements by considering it as an uncertain state variable.The solution addresses various challenges for cooperative localization, namely, the bandwidth issue, data association uncertainties, coordinate transformation overheads, and scalability.

The exteroceptive/infrastructure sensor, such as RADAR/GPS, is used as topology factor of factor graph. The configuration(i.e.,orientation and location)of the sensor is unknown,and the topology information (the distance between the unmanned systems) at time t can be calculated as presented,which is robust against outliers. In Ref., an approach based on factor graph and topology constraints was proposed, which introduces topology factors, and only considers the position relationship between targets, but not its shape.

The aforementioned approaches about topology factor and SMEs can solve the drawbacks of traditional cooperative localization, including bandwidth limitations and data association limitations. Moreover, it can even solve the transformation between local coordinates and global coordinates.

The factor graph based cooperative localization approaches are summarized in Table 4.

5. Implementation of factor graph

5.1. Comparison between factor graph and filtering approach

The factor graph based smoothing method has many advantages over traditional filtering techniques such as EKF or its variants. It can more easily combine asynchronous and delayed measurements of sensors with different rates, and can be less error-prone in highly nonlinear system.Some investigations have demonstrated these advantages.In Ref.,an experimental micro unmanned aerial vehicle system has been built and some experiments have been performed to prove the effectiveness of the factor graph method.Ref.comprehensively compared four GNSS/INS integrations using both EKF and FGO with the real dataset collected in urban canyons. Fig. 7(a) shows the experimental vehicle and sensors setup, and Fig. 7(b) shows the 2D trajectories errors from tightly-coupled integrations using EKF and factor graph during the test. The simulation result shows that the 2D mean error decreases dramatically from 8.03 m for EKF to 3.64 m for FGO, and the standard deviation also decreases from 7.15 to 2.84. According to the analysis, the superior performance of FGO compared with EKF is caused by three parts:(A) the multiple iterations; (B) the larger size of data applied in the optimization; (C) the re-linearization against all the states.

5.2. Engineering implementation

As the number of vehicles increases, data association has become more and more challenging.In Refs.,an approach which implements Symmetric Measurement Equations (SME)within factor graph was proposed. The proposed methods solve the data association, because they do not need to enumerate the association of the metric to the target. In addition,the Dedicated Short Range Communication (DSRC) distance information is represented as a novel DSRC distance factor in the factor graph,thereby achieving better state estimation.In Ref., the multi-sensor multi-target state estimation method was presented, on the one hand, to Generalize the Labeled Multi-Bernoulli (GLMB) filter, and on the other hand, to use the SME based on factor graph for cooperative localization. However, as the error covariance increases, the performance of GLMB filter decreases faster than the factor graph with SME. Subsequently, a novel cooperative localization method based on probability data association was

In order to utilize factor graph to implement navigation and localization, many researchers have developed toolkits, and the most popular ones are the Georgia Tech Smoothing andMapping (GTSAM)and Open Smoothing and Mapping(OpenSAM).GTSAM toolbox was designed by Georgia Tech,which is a BSD authorized C++ library based on factor graph that implements sensor fusion for robotics and computer vision applications, including SLAM, Visual Odometry,and Structure from Motion. It also provides a MATLAB interface that allows rapid prototyping,visualization,and user interaction.OpenSAM toolbox provides an industry-standard,factor graph sensor fusion reference implementation optimized for embedded systems.In addition,many scholars have implemented factor graph optimization using C++,C,MATLAB,Python and other languages.In the future,there may be more factor graph toolboxes for navigation and positioning.

Table 4 Factor graph based cooperative localization methodologies.

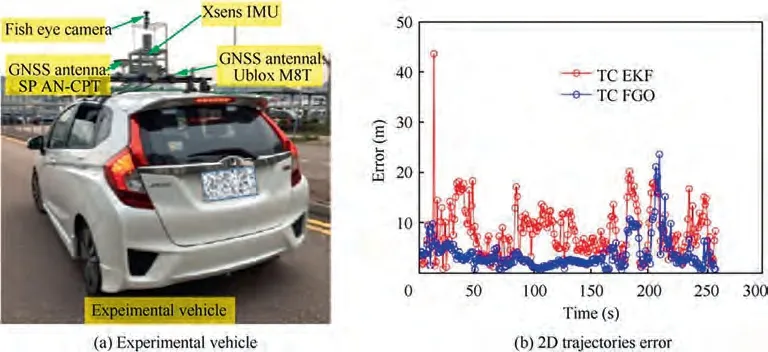
Fig. 7 GNSS/INS integrations using EKF and factor graph.75

Of course, these toolboxes have also been verified. In Ref., the proposed incremental smoother to the nonlinear sensor fusion system of actual unmanned aerial vehicle was firstly applied. Subsequently, a state-level hardware-in-theloop for small fixed-wing UAVs was designed by using incremental smoothing.In Ref.,the GTSAM toolbox was utilized to provide incremental smoothing and mapping implementation, which is used to estimate the position and attitude of the quadrotor. In Ref., the factor graph and GTSAM toolbox as a constrained optimization framework is feasible to solve linear and constrained nonlinear optimization problems. Moreover, a multi-satellite relative state estimation modeling and implementation method based on factor graph was proposedand implemented through GTSAM toolbox.These investigations further confirm the superiority of factor graphs and the availability of toolboxes such as GTSAM.

However,a complete factor graph optimization mechanism requires intense computations, which introduces a long delay for the optimization process to complete.Furthermore,designing a hardware platform suitable for factor graph optimization can maximize the effectiveness of this method. In Ref., an embedded Factor Graph (FG) inference engine that employs a neural-inspired discretization mechanism was presented,and the engine runs on a System-on-Chip(SoC)and is accelerated by its FPGA.Fig.8(a)shows the general overview of how to use the FG inference engine running on an SoC that can be used to control a robot. Fig. 8(b) shows a tailored module TE0720 produced by Trenz-Electronics. This method uses FPGA-ARM architectures and is proven to be useful. However, the method has two limitations: one is that it cannot achieve true parallel processing. Moreover, it is not easy to extend the IP core of the accelerator for a larger network whose nodes reside in another chip. Therefore, it is necessary to develop an embedded factor graph platform with continuity, modularity and platform-friendly feature.

6. Discussion and conclusion

In the past 20 years, significant progress toward the development of autonomous unmanned system has been made. This survey reviews the state of the art in factor graph based navigation and localization and provides a detailed overview of published papers,with a particular focus on recent and practical factor graph based navigation methods that have been implemented. The key conclusions of this paper are drawn as follows:

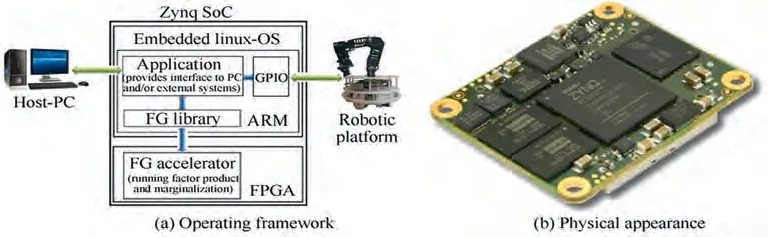
Fig. 8 Factor graph in system-on-chip.107

(1) Many papers have been published in the factor graph based navigation and localization areas, but very few of them have reported convincing experimental results.

(2) The factor graph optimization methods proposed at present have their own advantages and disadvantages, and there is great exploration value.

(3) Topology factor based cooperative localization is an active research topic, but the technologies developed so far are not reliable enough for real deployments.

(4) From this review, it is clear that the navigation method based on the factor graph is an important research topic and direction of the all-source positioning navigation system. The information fusion navigation combined with the factor graph method has a highly adaptable framework, which can satisfy the plug and play of various types for sensors, as new sensors are simply additional sources of factors that get added to the graph.The proposal of this method is beneficial to encouraging researchers to explore more advanced information fusion navigation filtering methods based on the characteristics of navigation system.

6.1. Navigation

Early research on navigation methods focused on Kalman filtering and its extended algorithms. However, these algorithms have flaws, and current navigation technologies have not yet reached the level of robustness and reliability required for real-world applications. In recent years, a brand-new navigation algorithm based on factor graph is proposed, which can solve the nonlinearity of navigation system,as well as the asynchronous, multi-rate or even variable-rate problems of multisensor fusion.Although many scholars study factor graph navigation and apply it in actual systems,we believe that there are some aspects of factor graph based navigation that have not really been investigated but are very important for real-world applications:

(1) Design of navigation estimator that combines filtering and factor graph in a back-end and front-end method based on filtering theory and factor graph.

(2) The factor graph focuses on the relationship between states, while traditional filtering methods concentrate on the states themselves.Various ideas of traditional filtering can be used for reference and applied to factor graph navigation theory.

(3) At present,most researchers study the theory of navigation optimization based on factor graph,and few scholars design the hardware platforms. In engineering practice, the development of hardware platform based on factor graph navigation should be increased.

6.2. Localization

For the success of the unmanned system,precise localization is an important criterion. Currently, it includes vision-based SLAM positioning, GNSS-based positioning, and cooperative localization methods. Many traditional solutions already exist such as EKF, MLE, and MAP estimation. But there are still some problems, including sensors data degradation, bandwidth limitations, coordinate transformations, etc. Although these challenges can be solved by the factor graph based localization methods reviewed in this paper, we find that most of the existing algorithms do not include much discussion about actual implementation,and few experimental results have been reported. Usually, only simulation results are provided based on ideal vehicles and operating conditions. Therefore, there is still much work to be done on developing and demonstrating efficient and precise positioning algorithms.

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

This work was supported by the National Natural Science Foundation of China (No. 61873207), the National Science and Technology Major Project, China (No. J2019-I-0021-0020), the Natural Science Basic Research Program of Shaanxi,China(No.2019JQ-344),the Science and Technology ProgramofXi’anCity,China(No.2019218314GXRC019CG020-GXYD19.3), and the Innovation Foundation for Doctor Dissertation of Northwestern Polytechnical University, China.