基于改进QEM的三维表面模型简化算法

马煜杰,王山东,欧阳涛

(河海大学地球科学与工程学院,江苏 南京 211100)

近年来,随着智慧城市建设的迅猛发展,三维场景可视化效果更加震撼,但也导致模型格网面片数量的急剧增加。因此,国内外学者对三维模型简化进行了很多研究:Garland等[1]提出模型简化时使用二次误差测度(QEM,quadric error mactrics)进行度量,该算法执行效率高,但简化后的网格较为均匀;周昆等[2]对三角形折叠进行简化时采用了QEM算法中的误差度量方式,提升了简化的效率,但计算新顶点位置具有不稳定性;Dassi等[3]通过计算简化前后两种模型的顶点位移变化,将变化值作为简化引子引入折叠代价,该算法对整体模型简化效果有一定程度的提升,但影响模型简化后的细节特征;段黎明等[4]为获取高精度的简化模型,提出将遗传算法引入到简化模型中,一定程度上增加了算法消耗时间;李胜辉等[5]将纹理、地形边界等特征引入QEM算法,作为约束因子保证了简化后三维地形的视觉效果和模型质量,该算法对于DEM整体简化效果较好;李世俊等[6]在几何特征中将顶点尖锐度引入折叠代价,结合纹理变化特征,使得模型局部细节特征得到很好保留,同时提出网格局部优化算法,保证简化质量,但算法简化时间增加;刘峻等[7]在边折叠算法中引入顶点曲率因子,提升网格质量,但未考虑顶点邻域的三角形面积,容易造成最优边的判断失误;黄佳等[8]提出了将顶点邻域法矢夹角变化作为折叠代价的渐进网格简化算法,保留了细节特征,但容易造成平坦区域的三角网简化顺序选择的混乱。

为了改善算法存在局部细节特征破坏明显,简化效率低等问题,提出一种改进的QEM简化算法,将顶点邻域面积、各顶点曲率及平展度引入权值的计算,更多地保留三维模型局部细节特征,有效地减少了三角面个数。

1 QEM算法

QEM算法是基于边折叠的简化算法,删除边(va,vb)并将顶点合并成新的点vnew,对三维模型网格进行局部重构,多次迭代进而减少模型的三角面个数完成简化。顶点分裂是边折叠的逆向操作,折叠与分裂过程如图1所示。

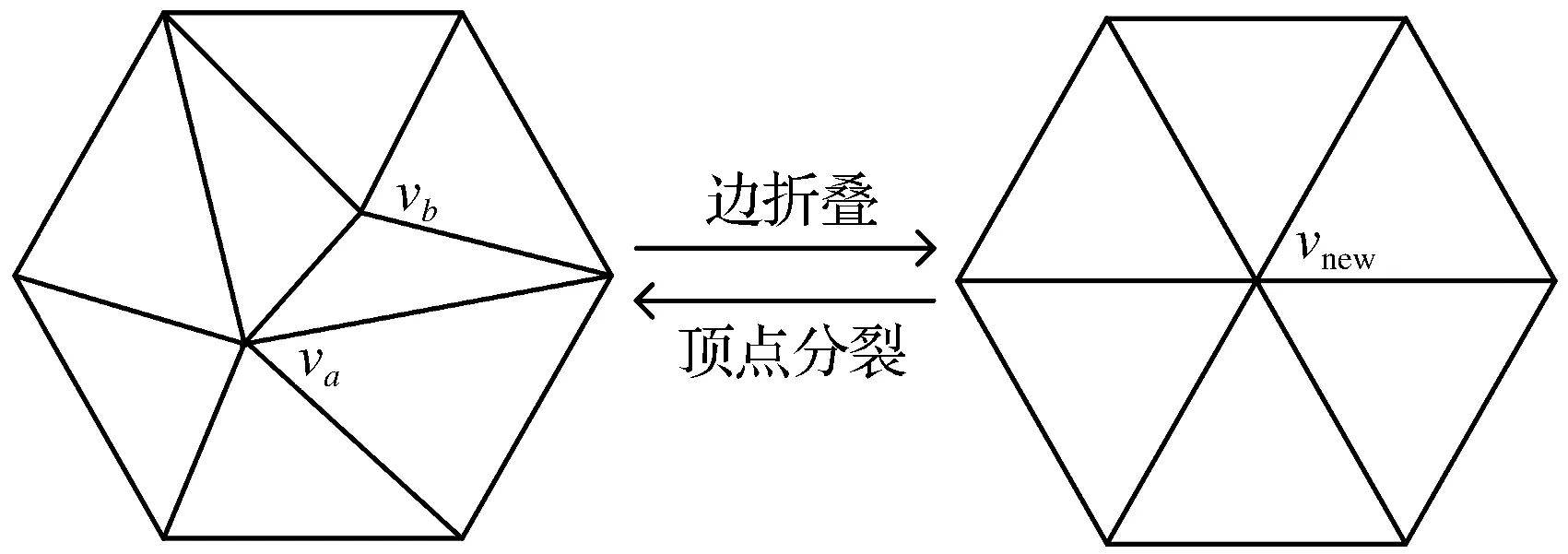
图1 边折叠过程Fig.1 Edge folding process

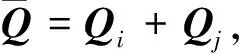
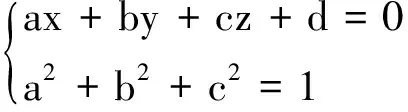
(1)

式(1)结果的误差矩阵又可以表示为

(2)

其中Kp可表示为

(3)

计算顶点v的一阶邻域的所有平面的Kp之和得到误差矩阵Q。

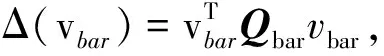
Δ(v)=q11x2+2q12xy+2q13xz+2q14x+

q22y2+2q23yz+2q24y+q33z2+

2q34z+q44。

(4)

求偏导后可计算新顶点vbar的坐标:

(5)

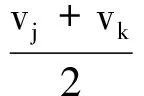
2 算法改进

2.1 顶点曲率

顶点的一阶邻域三角形所有法向量之和,用来计算该顶点的近似曲率,而顶点曲率则反映了模型中局部区域特征的明显程度[10],即可视化效果。在三维模型特征明显处或起伏较大处,曲率较大,且顶点很可能为拐点或折痕。

在三维模型中任取一个三角面T0,vi、vi-1和vi+1为该三角面的3个顶点,其单位法向量可表示为

(6)

对于三维模型某一顶点vn的顶点法向量nvn可表示为

(7)

进而求得该顶点处曲率的大小:

(8)

其中:ni表示顶点vi的一阶邻域面的法线向量。

2.2 顶点邻域面积

定义顶点v相关联的三角面包括T1、T2、T3、T4、T55个三角面,该顶点的顶点邻域面积SLR(v)可由上述5个三角形的面积计算得,即

(9)

其中:变量k为某顶点一阶邻域三角面的个数;Si表示上述邻域三角形中第i个三角形的表面积。

将顶点邻域面积SLR(v)求平均后,若值较小,表征该顶点附近的网格密度较大,特征较为明显,反之该处网格较为平坦。

2.3 平展度

顶点的平展度可通过计算所有一阶邻域边的二面角与边三角面数量之商得到,该简化因子可表征顶点周围区域是否光滑。为简化计算,顶点平展度采用共用顶点一阶邻域边的两三角面外法线夹角近似得出[11],其计算公式为

(10)

其中:变量m为某顶点一阶邻域三角面的个数;βn表示共用顶点一阶邻域第n条边的三角面外法线夹角。

综上所述,把顶点邻域面积、各顶点曲率及平展度加权3个简化因子加入到模型简化时每条边的误差代价中,最后计算求得折叠代价:

与既往教育有所不同，小学数学教育信息化的提出和实施，虽然具有广阔的前景，但是在教育工作和任务的具体实践过程中，还是要按照一定的原则来实施，这样才能在问题的有效解决、综合改进过程中，不断地创造出较高的价值。首先，小学数学教育信息化，必须按照多元化的原则来进行，尤其是在动态影响因素的作用下，有针对性地干预和引导，促使小学数学教育信息化的水平获得持续性的提升。其次，在小学数学教育信息化的运作过程中，应坚持大幅度地提升教育的综合效用，促使师生沟通交流更加频繁，教师要按照求同存异的方法来教育，这对尊重小学生的主体地位，能够产生良好的效果。

(11)

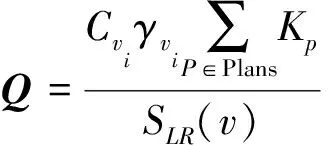
2.4 简化算法流程

三维模型简化过程中,关键是要选取简化因子,计算边折叠代价,保证其细节特征在简化后尽量不被破坏,同时提高模型的简化效率,算法流程如图2所示。

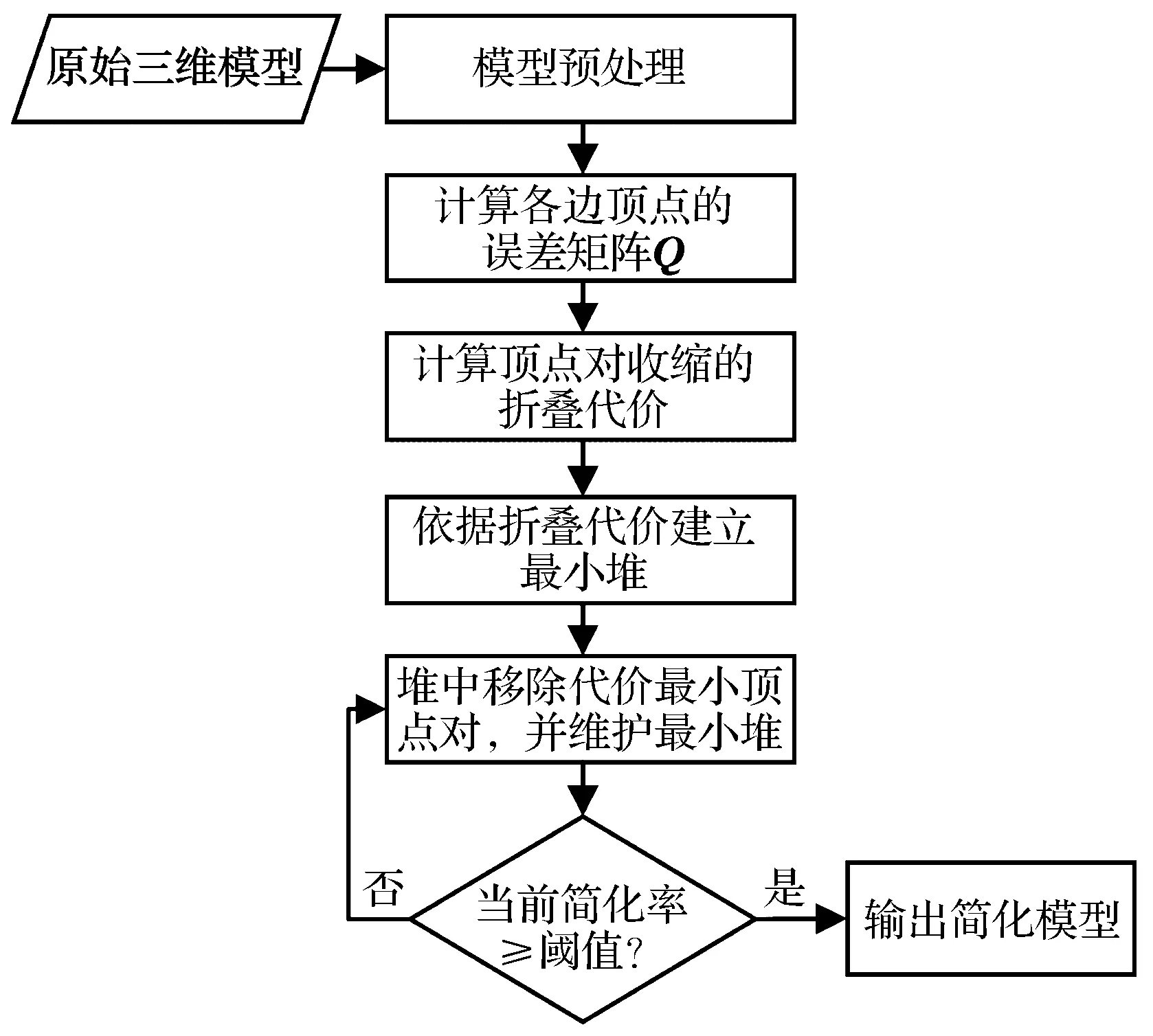
图2 算法流程Fig.2 Algorithm flow chart

首先,三维模型预处理是对每个三角面片顶点索引进行记录,并对算法中的阈值进行设定。其次,选择顶点曲率等简化因子,计算顶点的折叠代价,防止简化过程中细节特征的丢失。同时为了提高算法的效率,引入了最小堆结构,依据计算好的折叠代价建立最小堆,之后简化时只需要从最小堆中选取折叠边进行操作并对堆进行维护。最后进行迭代过程,输出简化的三维模型。

3 实验结果与分析

基于2.20 GHz Intel(R) Core(TM) i7CPU 16 GB内存的硬件环境,在Visual Studio 2017的开发平台下,基于OpenGL库实现算法,实验采用cow与古建筑2种三维模型进行实验探究:

(1) 通过比较QEM算法和改进算法在简化后的整体效果、局部特征以及算法效率等方面的差异,进而验证改进算法的性能;

(2) 检验顶点曲率、平展度以及顶点邻域面积在简化中的作用,通过剔除单个简化因子进行对比实验来验证。

3.1 算法性能比较

实验所使用的2种原始模型如图3所示,图3(a)为原始实验数据cow模型(共包含5 804个三角面),图3(b)为某古建筑的原始实验数据(共包含394 436个三角面)。

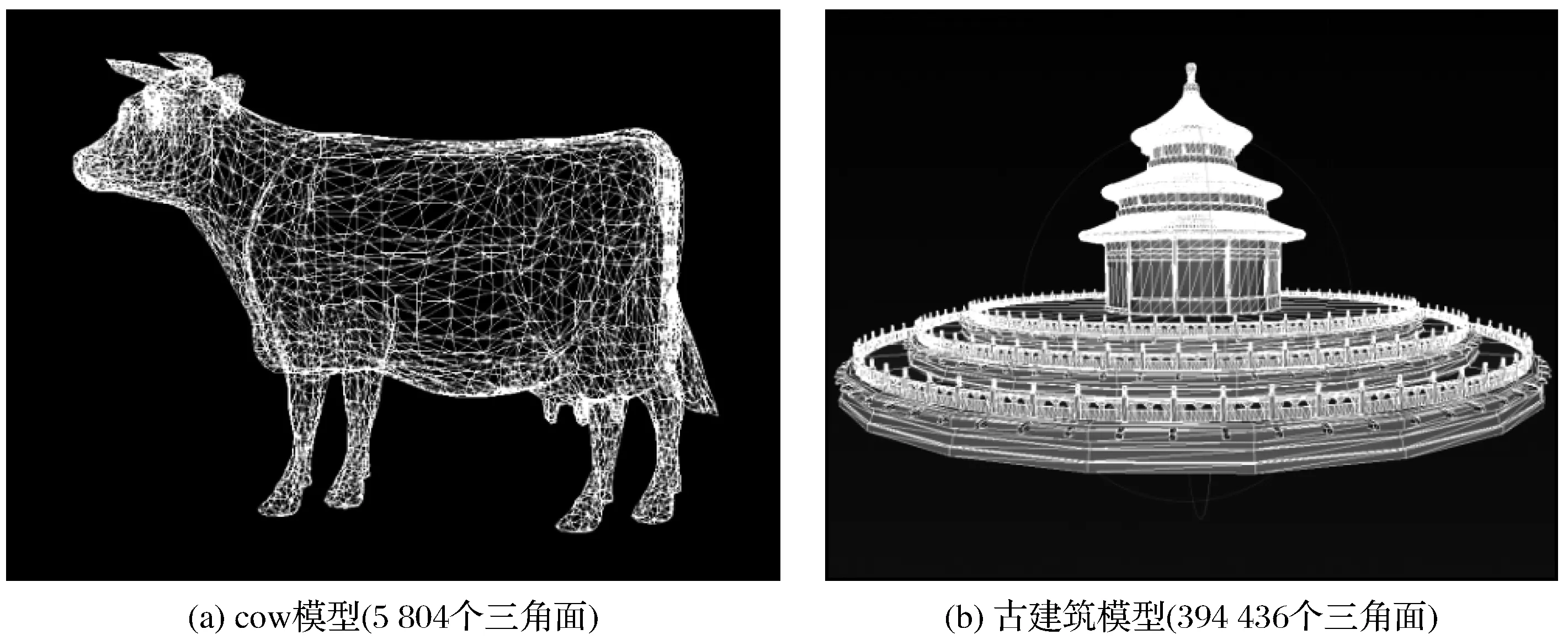
图3 原始模型Fig.3 Original model

对cow模型利用2种算法进行对比简化实验,当简化程度为50%时,由图4(a)可以发现QEM算法简化结果较为均匀,牛身体各部位三角网稠密大致相同,但使用改进算法简化后(见图5(a)),牛身等平坦区域简化效果更明显,在简化面数一致的情况下,牛角、牛蹄等部位三角面网更稠密。当简化程度为85%时,使用QEM算法简化后牛身部位仍然存在较为密集的三角面,对牛的某些局部特征(如牛角部位)不能较好地保留,存在一定程度的变形;相反使用改进算法简化后,牛身等特征较为平坦的区域其三角网会在不改变其形状的前提下得到很大程度的简化,牛蹄、牛角等部位保持了细节特征,改善了QEM算法简化网格均匀的问题。由表1可知,2种算法都极大压缩了三角网的数量,都能够简化4 928个三角面,但是改进算法中引入最小堆结构后,时间消耗明显缩短。

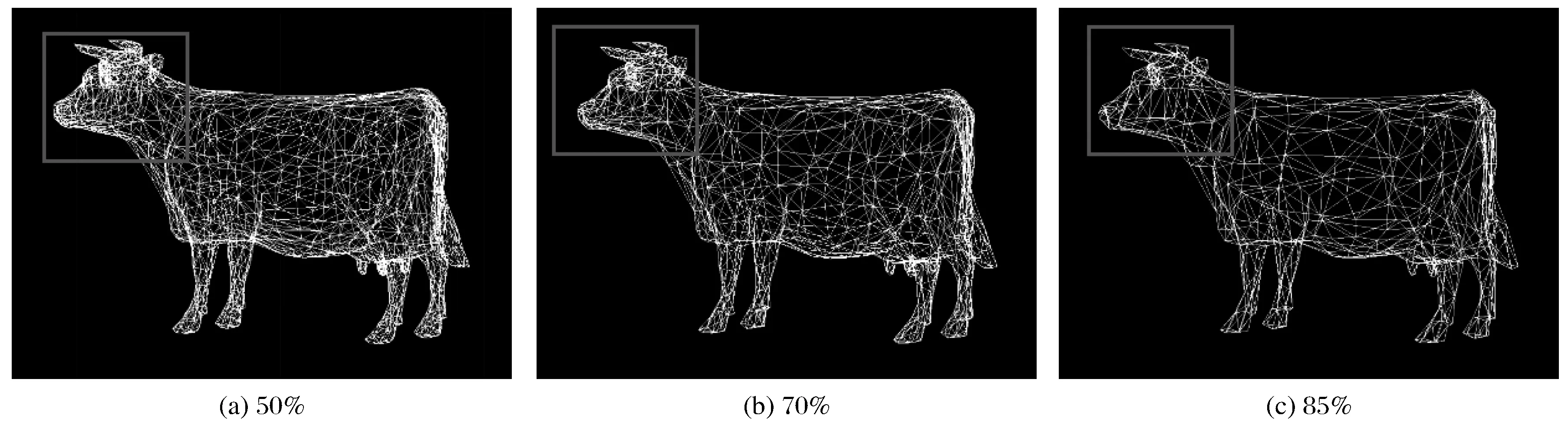
图4 cow模型简化效果(QEM算法)Fig.4 Simplification effect of cow model (QEM algorithm)

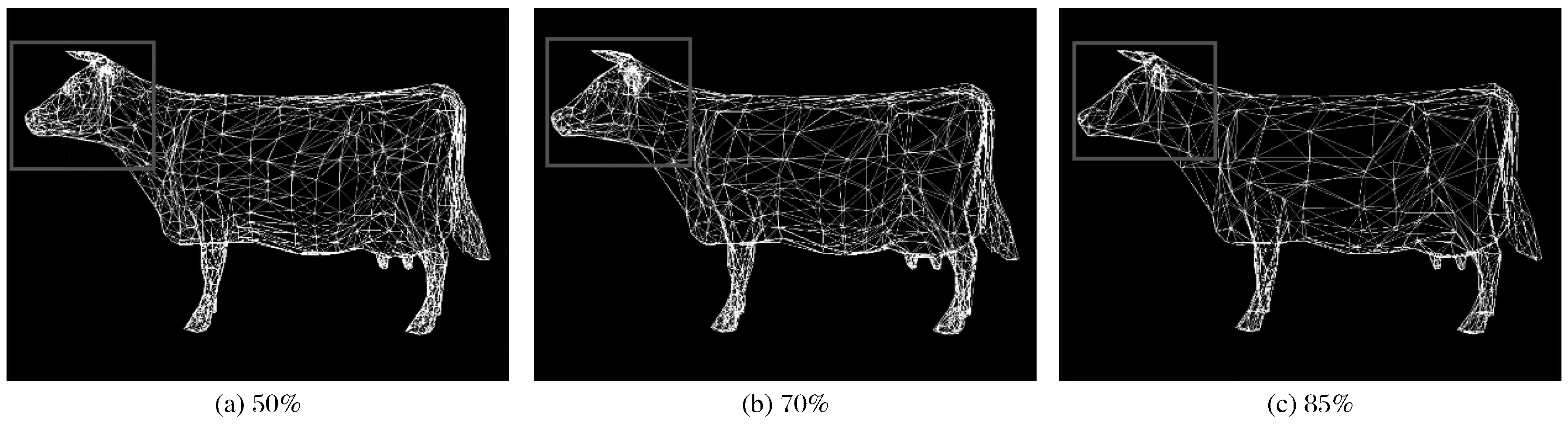
图5 cow模型简化效果(改进算法)Fig.5 Simplification effect of cow model (improved algorithm)

表1 cow模型简化效果统计

对古建筑模型使用QEM算法和改进算法进行简化,简化效果如图6、图7所示,简化效果统计如表2所列。

通过对古建筑模型使用2种算法进行对比简化实验,可以发现改进算法不仅减少了三维模型三角面片的数量,而且很好地保留了古建筑中的一些局部特征。当简化程度为50%时,由图6(a)可以明显看出QEM算法造成了古建筑的围栏部位2个半圆形空洞几何特征的破坏,改进算法很好地改善了上述问题;由图7(a)可以看出古建筑的栏杆的形状和数量在简化后能很好保留下来。当简化程度为70%时,由图6(b)可以看出利用QEM算法简化后围栏部位空洞基本上失去了视觉效果,台阶深色部位也开始发生变形。当简化程度为85%时,古建筑房屋整体轮廓特征较好,栏杆、台阶等区域都出现了一定程度的细节特征丢失,但改进算法的细节区域简化效果整体上好于QEM算法简化效果。由表2可知,2种算法都简化了335 151个三角面,在一定程度上提高了简化效率。总体而言,在同等简化率下模型的完整性与可视效果改进算法要高于QEM算法,给人以贴近真实的视觉效果,并提高了简化效率。

图6 古建筑模型简化效果(QEM算法)Fig.6 Simplification effect of ancient building model (QEM algorithm)

图7 古建筑模型简化效果(改进算法)Fig.7 Simplification effect of ancient building model (improved algorithm)

表2 古建筑模型简化效果统计

3.2 简化因子检验

改进算法引入顶点邻域面积、平展度以及顶点曲率3种简化因子来改进QEM算法,因此需要检验3种因子在简化过程中的作用。经分析发现,对于平坦区域,在简化时顶点邻域面积会使简化后可视化效果较好,因此分别剔除平展度和顶点曲率,比较二者的简化结果。

首先移除顶点曲率,保留平展度与顶点邻域面积因子,对古建筑三维模型进行简化,简化效果如图8所示。

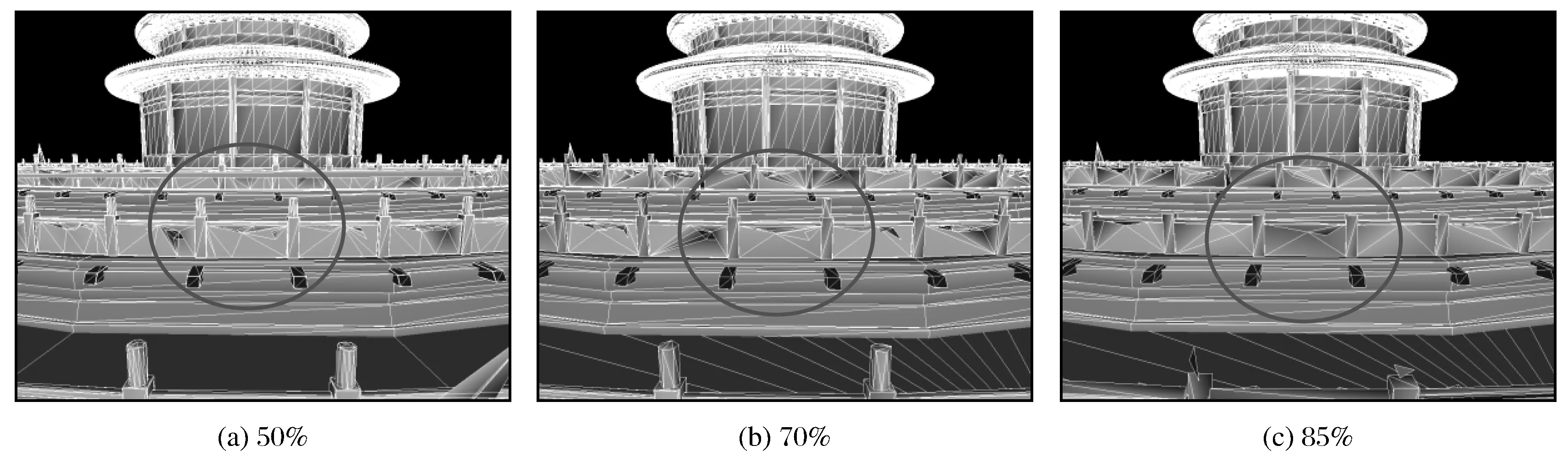
图8 移除顶点曲率加权的简化图Fig.8 Simplification results without vertex curvature weighting

当简化因子中剔除顶点曲率时,由图8可以看出,简化率为50%时一定程度上破坏了古建筑模型环绕护栏的局部特征,虽然整体轮廓并未发生较大的改变,但两栏杆之间的半圆形空洞简化后已经变得不可见;当简化率为85%时,局部特征就基本上丧失了视觉效果,但仍保持着模型的整体轮廓特征。这是因为基于顶点曲率可以判断顶点是否位于拐点等折痕区域,在简化过程中可以保留。

接下来移除平展度,保留顶点曲率与顶点邻域面积因子,对古建筑三维模型进行简化,简化效果如图9所示。

当简化因子中剔除平展度时,由图9可以看出,随着简化率的升高,古建筑物环绕护栏的细节特征丢失越严重。当考虑到平展度加权,进而会优先简化邻域三角形更为平滑的顶点,提升了简化效果。

图9 移除平展度加权的简化图Fig.9 Simplification results without flattening weighting

通过对比可以得到,顶点曲率加权能更好地保留模型局部特征,保留平展度虽然没有体现出更好的简化效果,但结合顶点曲率其效果可以得到进一步提升。

4 结语

基于QEM的边折叠算法,首先在二次测度误差中加入了顶点邻域面积、各顶点曲率及平展度3种简化因子,目的是在简化三维模型时优先移除不明显、不重要的模型格网顶点,对三维模型明显程度较高的顶点进行保留,较好地保留模型的细节特征;同时在算法中引入最小堆结构,依据计算好的折叠代价建立最小堆,有效提高了三维模型的简化效率。本文改进算法在减少表面模型三角面数量的同时,能有效防止模型的部分细节特征在简化时被破坏,保留了模型的视觉效果和几何特征,提升了简化后模型的质量,提高了算法效率。