基于多新息CDKF算法的锂电池SOC估计

达杨阳，万佑红，张帅帅

(南京邮电大学自动化学院、人工智能学院，江苏南京 210023)

锂离子电池因其比能高、负载能力高、自放电率低等优点[1]，在电动汽车和储能系统中得到了广泛应用。SOC作为电池内部状态量，无法直接量测，只能通过电池外部电压和电流进行估计[2]。对SOC的不准确估计很容易导致电池过充或过放，从而危害电池本身并产生安全问题[3]。

SOC估计中常用的方法有：(1)安时积分法[4]和开路电压法[5]，理论简单且易于实现，但受限于精度和测量条件;(2)人工神经网络[6]，模糊逻辑建模[7]，模糊神经网络[8]等机器学习方法,需要大量精确数据，且结果易受不同数据集影响;(3)Kalman 滤波法，其衍生算法在SOC估计中应用最为广泛。

锂离子电池实质上是非线性系统，由于模型误差和量测仪器偏差等因素，系统中常包含不确定性噪声。标准Kalman滤波极度依赖于模型的准确性，鲁棒性较差。扩展Kalman 滤波(EKF)[9]对非线性函数作一阶泰勒展开处理，忽略了二阶及以上误差，在系统非线性强度较大时误差比较明显。无迹Kalman 滤波(UKF)[10]采用sigma 点近似而非泰勒级数展开，避免了对非线性函数解析求导，但模型阶数增加会增加sigma点数量，增大计算复杂度。中心差分卡尔曼滤波方法(CDKF)[11]以中心差分代替泰勒公式中的一阶和二阶导数，避免复杂的求导运算，精度与UKF 相仿。H∞滤波[12]通过设计合适的代价函数J来确保系统状态在不确定性噪声影响下不会超出设定的性能边界，将噪声对状态估计的负面影响降到最低。但H∞滤波并非最优估计，算法估计结果偏保守。

本文采用等效电路模型对锂离子电池进行分析。为在模型精度和计算复杂度间取得平衡，建立二阶RC 等效电路模型，提出一种基于多新息的中心差分Kalman 滤波方法，将传统Kalman 滤波方法的标量新息拓展为新息向量，根据各历史信息与当前时刻数据关联程度赋予相应权值，有效提高SOC估计精度和鲁棒性。

1 锂离子电池建模与参数辨识

1.1 模型选取与建立

本文建立的二阶RC 等效电路模型如图1 所示。

图1 中，Uoc为开路电压；Ut为电池端电压；R1和C1分别是电化学极化电阻、电容；R2和C2分别是浓差极化电阻、电容；R0为内阻；I为电池电流，充电为正；U1为电阻R1端电压；U2为电阻R2端电压。

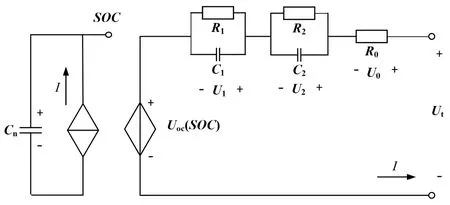
图1 二阶RC 等效电路模型

根据基尔霍夫定律和安时积分法表达式，对等效电路模型建立状态空间方程为：

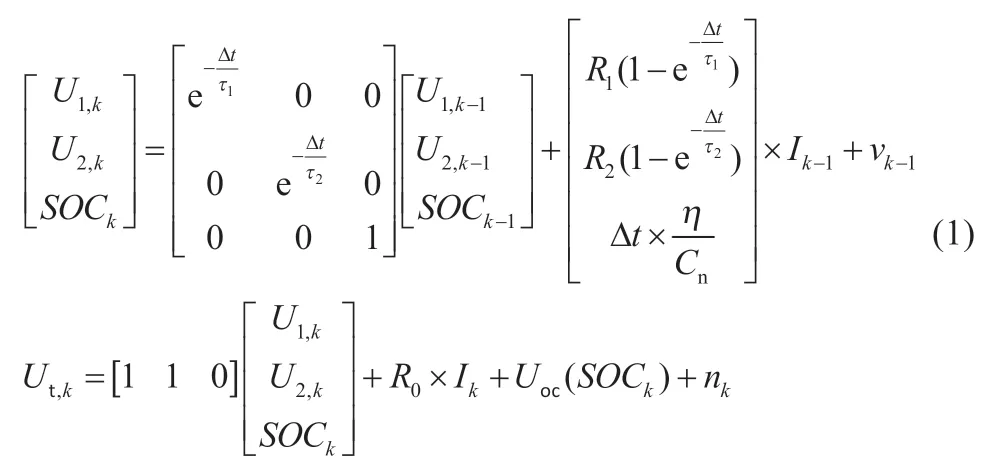
式中：Cn为电池的容量；η 为库仑效率系数；Δt为采样周期；vk-1和nk分别为k-1 时刻过程噪声和k时刻量测噪声；τ1和τ2为RC 网络的时间常数，τ1=R1′C1，τ2=R2′C2；Uoc()为Uoc关于SOC的函数；Ik-1为k-1 时刻的电流，Ik同理。

1.2 SOC-OCV 曲线

本文基于BT-2018D 国产锂电池测试系统、电池数据采集系统对LG18650HG2 三元锂电池进行实验。单体电池额定容量3 Ah，额定电压3.6 V，电压检测误差±1.5 mV，温度检测精度±1.5 ℃，数据采样频率为10 Hz，实验在25 ℃环境中进行。

对电池进行0.5C恒流充放电，充电或放电后将电池静置一定时间以获得准确开路电压Uoc。图2 为对充电和放电SOC-OCV曲线均值进行拟合[13]，拟合式如下：

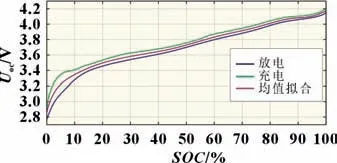
图2 SOC-OCV曲线

1.3 带遗忘因子递推最小二乘法

由于锂离子电池模型中参数会受到环境温度和电池老化程度的影响，参数会随SOC变化而变化，因此采用最小二乘法进行参数辨识。带遗忘因子递推最小二乘法(FFRLS)[14]在递推最小二乘法(RLS)的基础上引入遗忘因子λ，降低旧数据对参数估计的影响，避免数据饱和现象。λ 一般取值0.90～1.00 之间，本文取值为0.96。FFRLS 表达式为：

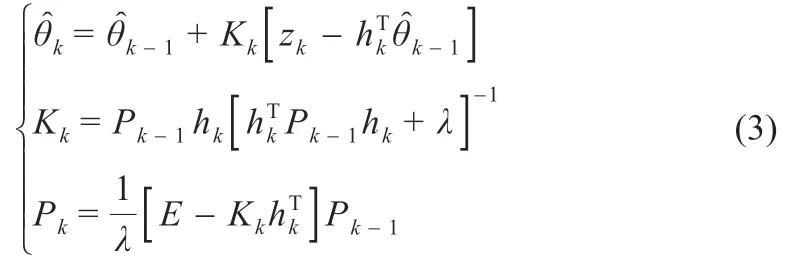
式中：θk为待辨识参数向量为估计参数向量；Kk为增益向量；zk为系统实际输出值；hk为数据向量；T 为矩阵或向量的转置；Pk为估计误差协方差矩阵；E为单位矩阵。

1.4 模型参数辨识

锂电池通常可视为非线性时变系统，式(1)对应的脉冲传递函数为：

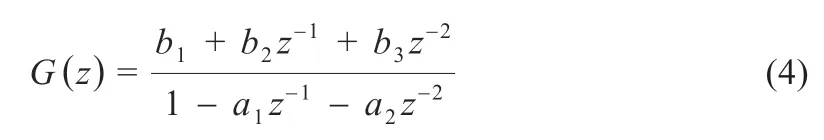
式中：a1，a2，b1，b2，b3为AR 模型待辨识参数。

令Uk=Ut，k-Uoc，k，由脉冲响应不变法将式(4)转换为差分方程：

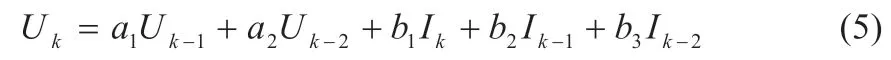
式中：a1，a2，b1，b2，b3为AR 模型待辨识参数，这些参数与二阶RC 模型中的电阻和电容可相互转换。令Zk=Ut，k-Uoc，k，=[Zk-1,Zk-2,Ik,Ik-1,Ik-2]，待辨识参数向量a1，a2，b1，b2，b3]。设为合理初值，P0为103×E5×5，E5×5为5 阶单位矩阵。对DST 工况数据应用FFRLS 进行参数辨识，得到各电阻电容实时值。将模型输出值与实际值进行对比，仿真结果与实测结果对比及误差见图3。

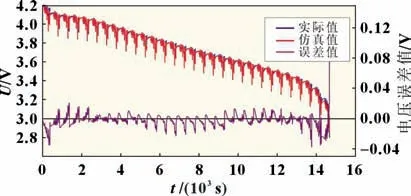
图3 模型输出与实际电压对比及误差

从平均相对误差(MRE)、绝对误差均值(MAE)和均方根误差(RMSE)三方面进行评测，各指标定义如下：

式中：N为采样点总数。由参数辨识结果得MRE为0.148 68%，MAE为5.4 mV，RMSE为7.7 mV，辨识精度较高。

2 基于MI-CDKF 的SOC 估计算法

相比于EKF 需要进行求导运算，CDKF 方法采用Sterling差值公式，采用中心差分替代EKF 的一阶和二阶导数。中心差分通过对非线性函数特定点的值进行计算，避免了复杂的求导运算，CDKF 的迭代流程见图4。

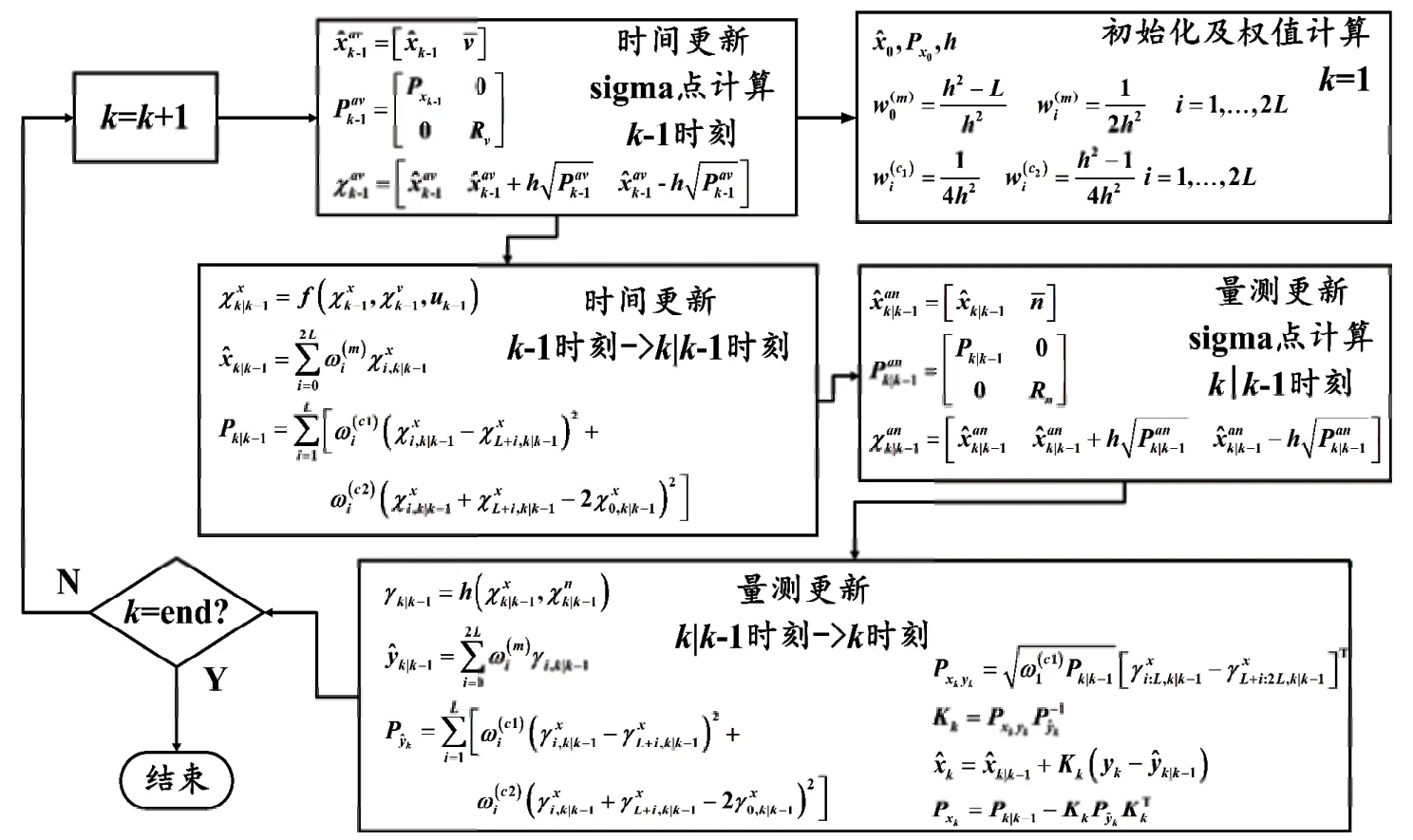
图4 CDKF迭代流程图

图中：xav=[xTvT]T，xan=[xTnT]T，h≥1 为中心差分步长，L为增广状态向量维数，Rv为过程噪声协方差矩阵，Rn为量测噪声协方差矩阵，(·)2为向量外积简写，如a2=aaT。

为对过去时刻历史信息加以利用，引入多新息理论，与中心差分Kalman 滤波结合。将标量新息扩展为新息向量，同时将CDKF 的增益向量扩展为增益矩阵Kp,k：

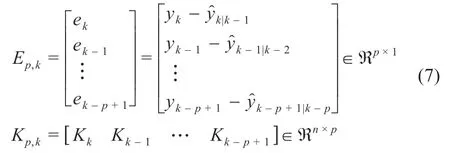
式中：p为新息向量长度；Kp,k表示长度为p的Kalman 增益矩阵；Kk-p+1为相对于当前时刻过去p-1 时刻的增益向量。

由量测更新中单独提出后验估计式：

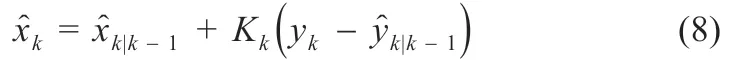
将标量新息和增益向量换为扩展后的新息向量和增益矩阵，表示如下：

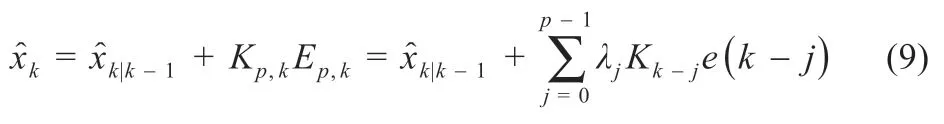
式中：λj的取值会影响到MI-CDKF的性能改善程度。文献[15]提到新量测数据应当比旧量测数据赋予更大权重。为保证当前数据的更新误差作用占主导地位，对λ 值的取值应当遵循以下原则：

式中：0＜h＜1，h趋于1 时，旧数据权重等同当前数据，h趋于0时退化为CDKF。当多新息向量长度≤3 时，为突出当前数据作用，h值根据经验可取0.80 以内的值。多新息长度大于3时，偏重对历史信息的考虑，h值根据经验可取0.50 以上的值。

出于计算量考虑，多新息向量长度一般限制在2～8 以内，因此对λ 值的选取如下：

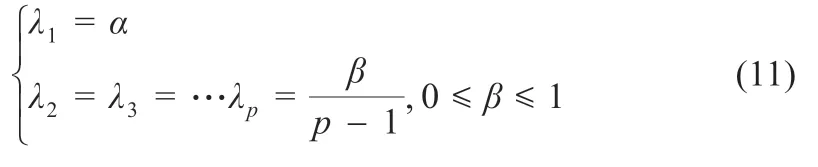
式中：α，β 值选取视多新息向量长度而定。

3 实验结果与分析

实验采用UDDS 工况对电池进行放电，并在此工况数据下验证本文算法。为比较MI-CDKF 和EKF、UKF、CDKF 的鲁棒性和收敛速度差异，将SOC初值设置为0.7。其中收敛速度用调节时间表示定义为：ts=max{t|(SOCes-SOCref)≥±5%}，式中SOCes为SOC估计值，SOCref为参考SOC值。为了在提升估计性能的同时不过多增加计算量，扩展新息向量长度取2、3、4 进行比较。

基于式(11)的参数选取准则，为兼顾收敛速度和估计精度，通过多次实验获取较为合理的参数区间，见表1。

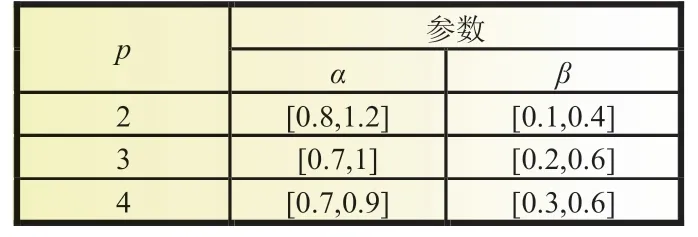
表1 不同长度新息向量合理参数区间

表1 中参数在给定区间内收敛速度和估计精度都有所提升，但参数的选择对收敛速度和估计精度的影响有偏重性。为兼顾两者，当p=2 时，选取α=0.9，β=0.3；p=3 时，选取α=0.8，β=0.4；p=4 时，选取α=0.7，β=0.4。对三种不同新息长度的MI-CDKF 进行仿真。实验结果如图5 和图6 所示。为便于观察估计精度和收敛速度，图5 和图6 加入了局部放大图。

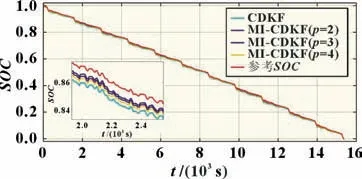
图5 不同p值下SOC估计结果

图5 中，CDKF 算法引入多新息理论后，估计精度得到了改善，其中p=3 时改善精度最佳。由图6 可见MI-CDKF 的收敛速度快于标准CDKF，同时估计精度均得到不同程度改善。表2 显示了不同p值下CDKF 的性能对比。对比各性能可见多新息向量长度为3 时效果最佳。

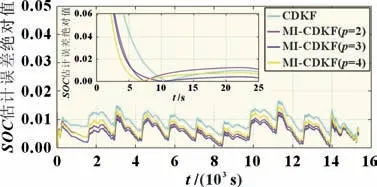
图6 不同p值下SOC估计误差

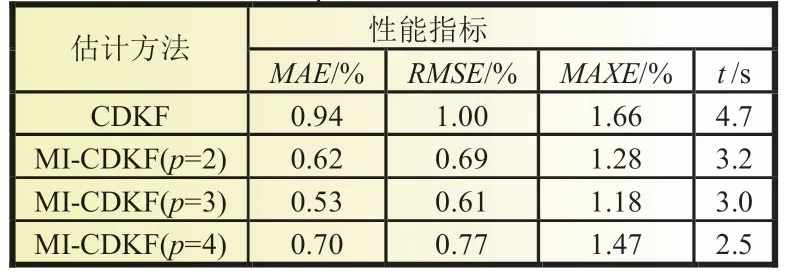
表2 不同p 值下CDKF 性能对比

为验证MI-CDKF 对不同SOC初值的鲁棒性，将SOC初值分别设置为0.3、0.5、0.7，得到的仿真结果如图7 所示。其中SOC=0.3 时调节时间为11.7 s，SOC=0.5 时调节时间为7.1 s，SOC=0.7 时调节时间为3 s，MI-CDKF 方法对不同SOC初值均具有较强鲁棒性。

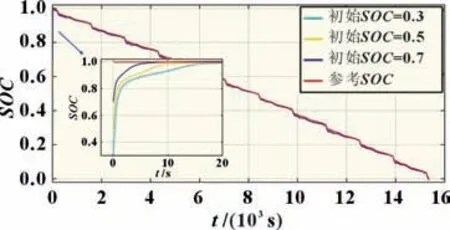
图7 不同SOC初值对比

将MI-CDKF(p=3)与EKF、UKF 和CDKF 进行比较，对上述方法均设置过程噪声协方差矩阵Q为diag([0.01 0.02 0.000 01])，其中diag表示对角阵，量测噪声协方差矩阵R为0.01。结果如图8 和图9 所示。

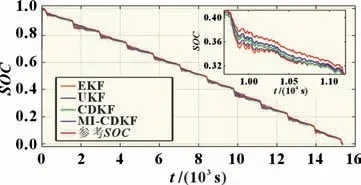
图8 不同SOC估计方法结果

图9 不同SOC估计方法误差对比

图8 和图9 中可以看到，MI-CDKF 在收敛速度和估计精度上都明显优于其他三种方法，四种方法的性能对比见表3。

表3 显示，MI-CDKF 方法比起常用的EKF、UKF 和CDKF方法在绝对均值(MAE)、均方根误差(RMSE)、最大误差的绝对值(MAXE)和收敛速度上均更有优势。

表3 不同SOC 估计方法性能对比

在实际电池管理系统中，传感器的误差主要有系统误差和随机误差，随机误差可通过Kalman 滤波算法予以较好抑制，而系统误差可以看作是加在测量值上的偏移值[16]。考虑到电池管理系统中常用电压传感器最大漂移范围不超过0.01 V，电流传感器最大漂移范围不超过0.1 A，为验证所提方法鲁棒性，分别在电压和电流上人工加入固定电压误差和电流误差，最后将两种误差合并加入。图10 显示四种不同状况下MI-CDKF(p=3)方法SOC估计性能的对比，其中M1 表示MI-CDKF 无电压电流漂移情况，M2 表示MI-CDKF 带电压漂移情况，M3 表示MI-CDKF 带电流漂移情况，M4 表示MICDKF 带电压电流漂移情况。

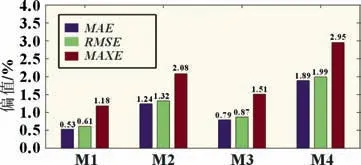
图10 四种情况下MI-CDKF性能对比

由于实际运行中电压信号和电流信号的最大漂移范围小于设定值，因此此法在实际应用中性能应优于实验中设定情况下测试所得性能。MI-CDKF 在传感器带漂移情况下依旧保持一定鲁棒性。

4 结论

根据锂离子电池的特性，建立了二阶RC 等效电路和对应的非线性状态空间方程，采用带遗忘因子的递推最小二乘法(FFRLS)对电池相应参数进行辨识，并将多新息理论引入中心差分卡尔曼滤波(CDKF)。首先对比不同新息向量长度下的多新息中心差分卡尔曼滤波(MI-CDKF)和标准CDKF 的性能，当p=3 时，MI-CDKF 的改善效果最佳。其次在不同SOC初值下验证MI-CDKF 的鲁棒性，并将MI-CDKF 与传统的EKF、UKF 和CDKF 进行实验对比，结果表明MI-CDKF 在估计精度和收敛速度方面均优于传统方法。最后在传感器漂移现象中验证了MI-CDKF 的鲁棒性。