基于双向GRU和H∞滤波器的SOC复合估算

桂 阳，周 飞，杨 文，陈 星，李康群

(南京航空航天大学直升机传动技术国家级重点实验室，江苏南京 210016)

随着能源短缺和环境恶化，新能源开发利用越来越重要。在电动汽车领域，锂离子电池清洁高效、能量密度高、循环性能好，已成为电动汽车储能装置的首选。储能锂离子电池组通常配备电池管理系统(BMS)，它能监视电池组状态，并为合理利用EV 车辆电池组能量提供条件，而准确估计电池荷电状态(SOC)是BMS 关键技术之一[1]。

SOC通常用来描述电池的剩余电量，可以用当前电量和额定电量的比值来表示，准确实时地估计SOC非常困难。目前，SOC估算通常用放电实验法、库仑计数法、模型驱动法、数据驱动法等[2]。放电实验法估算SOC步骤是，用恒定电流将电池放电至截止电压，计算得到电池当前的剩余容量，求出剩余容量和标称容量的比值，即为电池组SOC。该方法简单易行，结果也较为准确，但在车辆上无法实时在线估测，实际应用困难[3]。库仑计数法可通过累计流入或流出锂离子电池的电荷总数量来计算当前的SOC，这是可以通过积分型计算软件来实现。要想准确估算当下SOC需要两个前提：其一是给出的初始SOC值要准确，其二是用于计算的测量电流值与真实值之间的误差足够小。但行驶车辆很难获得这个准确的初始值，电池工作过程中测量电流传感器必然存在的误差会随时间累积产生较大误差。因此，该方法局限性较大[4]。

模型驱动法主要包括卡尔曼滤波法及其衍生算法。卡尔曼滤波是应用于估计动态线性系统内部状态的最佳算法之一。该算法实际上属于递推算法，其本质是通过系统输入输出观测数据来对动力系统的状态做出最优估计。卡尔曼及其衍生算法能够实时估计锂离子电池SOC，但需要搭建准确的电池模型，而这是一项非常困难地工作。

数据驱动的方法不依赖任何电池的物理、化学或热模型。它可以通过学习电池SOC和学习工作中电池的电压、电流、温度等参数的非线性关系，通过输入电压、电流、温度等特征，来直接在线估计SOC。常见的数据驱动方法包括支持向量机、人工神经网络、模糊逻辑等[5-6]。人工神经网络因其强大的非线性拟合效果可以很好地模拟电池内部的复杂结构，因而得到广泛应用，主要包括BP 神经网络、循环神经网络等，但是基于数据驱动的方法目前仍然存在着准确度不足、鲁棒性较差等缺陷。

针对以上问题，本文提出双向GRU(BidiGRU)神经网络和H∞滤波相结合的SOC估算方法。相较于卡尔曼滤波算法，本方法简化了SOC的估计流程；相较于神经网络算法，本方法提高了估计精度和鲁棒性。将锂离子电池放电过程中每一时刻的电压、电流、表面温度作为BidiGRU 神经网络的输入，对应时刻的SOC值作为输出，用北京动力循环工况(BJDST)对模型进行训练，用补充联邦测试程序驾驶时间表(US06)进行测试，再将H∞滤波器和BidiGRU 神经网络结合起来，滤除BidiGRU 神经网络的估计噪声，进一步提高估计精度和鲁棒性。

1 BidiGRU 神经网络结合H∞滤波器的复合估算

1.1 BidiGRU 神经网络

循环神经网络(RNN)是一类常用于处理序列问题的神经网络，普通的RNN 由于相邻的上一个时间步都对下一个时间步造成影响，在使用梯度下降法训练的过程中，会造成梯度消失和梯度爆炸的结果。梯度爆炸可以通过设置一个阙值来截取超过该阙值的梯度，但梯度消失往往难以预测，从而使普通的RNN 在处理长期依赖问题上效果不佳。LSTM 和GRU 神经网络的出现可以完美地解决这个问题[7]。GRU 在结构上较LSTM 更为简单，参数更少，在训练过程中更不容易出现过拟合，因此往往在大多数情况下GRU 的表现要优于LSTM。GRU 单元由更新门(update gate)和重置门(reset gate)组成，其前向传播公式为：

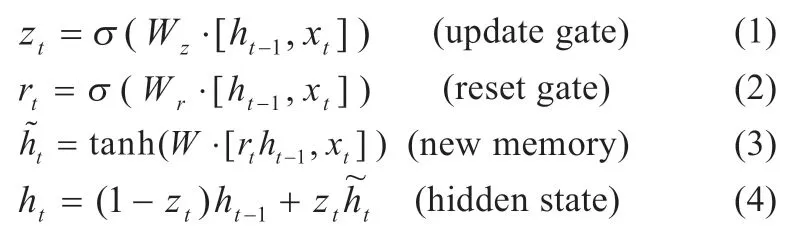
更新门(update gate)用于控制历史信息对当前时刻的影响，决定了模型要将多少过去的信息传递到未来，其中xt为t时刻的输入向量，ht-1为前一时间步的信息，Wz为权重矩阵，这一步至关重要，因为模型能够决定从过去复制所有的信息来降低梯度消失的风险。重置门(reset gate)用于控制历史信息的筛选，决定了有多少历史信息被遗忘，其中xt为t时刻的输入向量，ht-1为前一时间步的信息，Wr为权重矩阵。再将重置门的结果rt与上一时刻的信息ht-1经过线性变换来确定保留和遗忘的信息，再与当前时刻的输入与权重的乘积进行相加，将这部分的计算结果投入双曲正切函数(tanh)中，得到当前时刻的记忆，接着将当前时刻记忆与更新门和前一时刻记忆进行整合最终输出当前时刻的信息ht，并将其传递至下一个单元[8]。无论何种单向RNN，都存在着一个局限性，即在任一时间步t中，只能获取当前时刻之前的历史信息，在这之后的时间步信息，模型将无法学习到。因此，我们引入了双向循环神经网络(BidiRNN)，其结构图见图1。图1 中的单元为GRU 单元，ht和′分别为t时刻正向和反向序列中神经元所存储的记忆信息[9]。

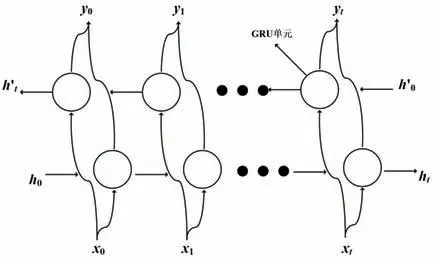
图1 BidiGRU结构图

1.2 基于BidiGRU 神经网络的SOC 估算模型

锂离子电池工作过程中的SOC变化是连续的非线性变化，是一个时间序列。当前时刻的SOC受过去和未来时刻SOC值的共同影响，这一点满足BidiGRU 神经网络的应用条件。因此，搭建了基于BidiGRU 神经网络的SOC估算模型，其结构见图2。输入层中把实验测得的电压、电流、电池表面温度作为输入。

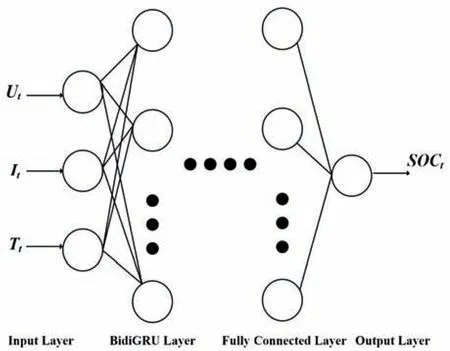
图2 BidiGRU-SOC估算架构

BidiGRU 层可以采用一层或多层，再通过一个全连阶层输出t时刻的SOC值，训练过程中的损失函数为均方误差函数(MSE)：

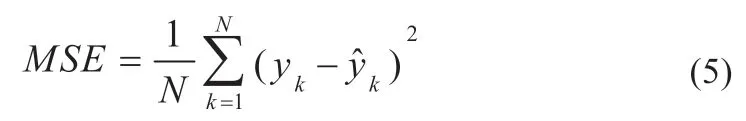
式中：N为序列的长度；yk为任一时刻真正的SOC值为任一时刻BidiGRU 的SOC输出值。使用梯度下降法进行训练，采用Adam 优化器，使用批量训练的方式，批量大小为30，经过调试后选择前50%的数据的学习率为0.001，后50%的数据的学习率为0.000 01。为了防止训练发散，数据集的输入使用式(6)进行归一化至[-1,1]区间内。

在完成训练之后，采用同样的归一化方法对测试集数据进行归一化，采用平均绝对误差(MAE)和均方根误差(RMSE)来对神经网络的性能进行评判。

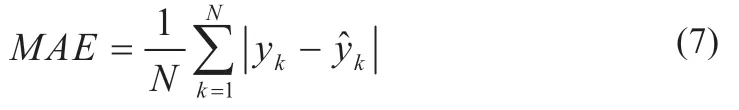
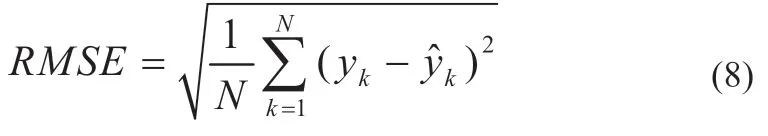
1.3 H∞滤波器

H∞滤波波器是卡尔曼滤波器的一个变种。卡尔曼滤波器是一种利用线性系统状态方程，通过系统输入输出观测数据，对系统进行最优状态估计的一种算法。最优状态估计过程就是滤波过程[10]。卡尔曼滤波的变种有很多，如EKF、UKF等。与EKF、UKF 这些滤波器不同的是，H∞滤波是专门为鲁棒性所设计的滤波。它通过最小化最大估计误差来进行滤波，可以达到极佳的鲁棒性[11]。H∞滤波的核心思想是保证系统的估计误差的范数小于所有可能的扰动。

假设我们有一个标准的线性系统：

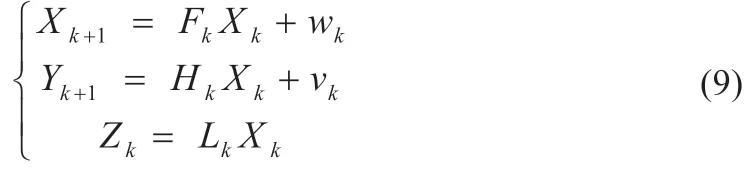
式中：Xk、Yk分别为系统的状态向量和观测向量；wk、vk为噪声项，它们是随机的，且统计特性未知；Fk为状态转移矩阵；Hk为测量矩阵；Zk为我们想要估计的状态的线性组合；Lk为一个满秩的由设计者自己定义的矩阵。

在H∞滤波中，我们定义了如下的代价函数：

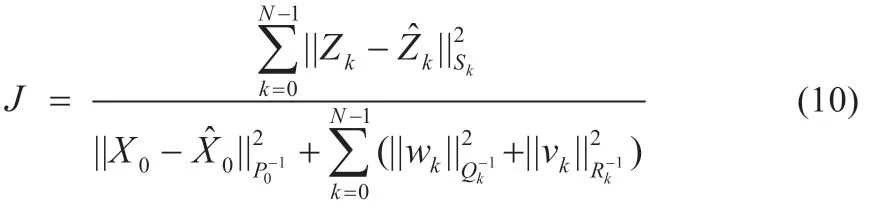
式中：P0、Qk、Rk为设计者基于特定问题所选择的对称正定矩阵为状态的估计值和初始值。直接最小化J是非常困难的，所以我们选择了一个性能边界，同时寻找一个估计策略使之满足这个阙值，换言之，我们想找到一个，使之满足：

式中：θ 为用户指定的性能边界[12]。

1.4 基于H∞滤波器的SOC 估计优化

在SOC估计中，将BidiGRU 神经网络作为观测器，其输出的结果作为观测方程，以安时积分法作为系统的状态方程，对SOC的估计结果进行优化：

状态方程：

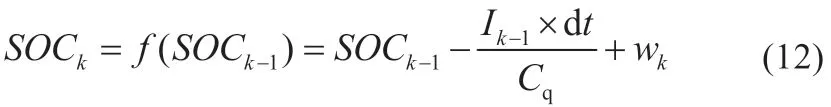
观测方程：

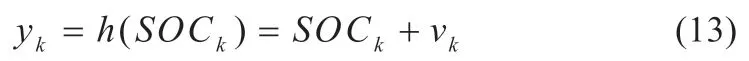
式中：Ik为k时刻的电流；Cq为标称容量；dt是采样间隔；wk、vk分别为k时刻状态方程和观测方程的高斯噪声，其高斯分布分别为wk～N(0,Q)、vk～N(0,R)。Q和R分别设为10-6、10-2，θ 设为10-4，采样间隔dt为1 s，初始SOC值SOC0设为1，将优化过后得到的SOC值作为最终的SOC估计值。

2 实验方法

使用21700 型锂离子电池作为实验电池，在电池动态测试系统中模拟电池的充放电循环并记录每时刻的电压和电流数据，通过高低温试验箱模拟不同的电池工作环境温度，通过无纸温度记录仪测得电池工作过程中的表面温度，详细的实验设备如图3 所示。为了模拟电池的实际工作过程，本实验选用了BJDST 工况对模型进行训练，用US06 工况进行测试，详细的BJDST 工况、US06 工况如图4 所示。

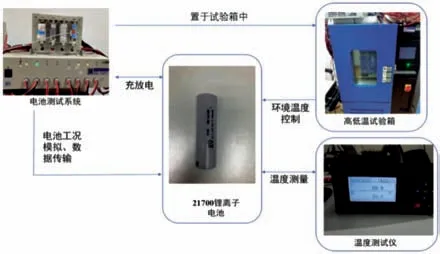
图3 锂离子电池测试系统

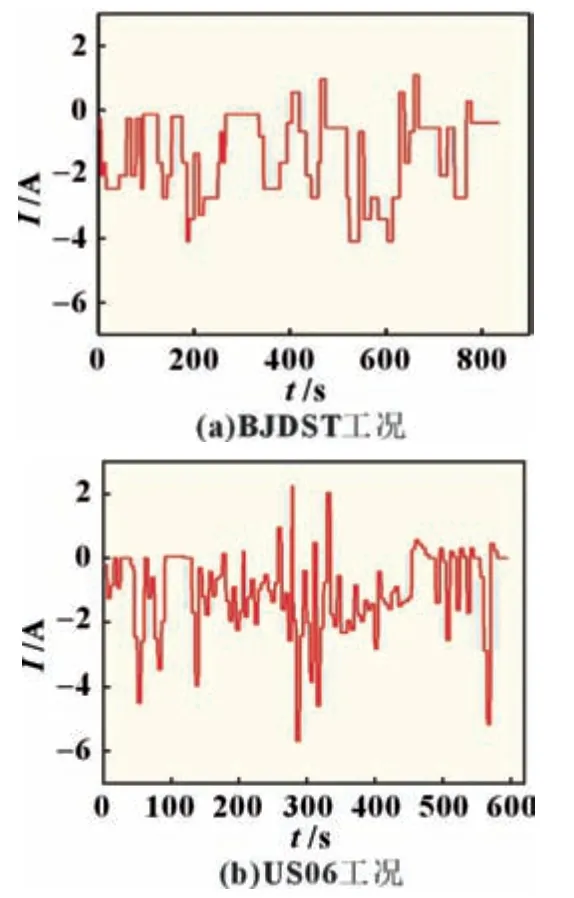
图4 电池工况电流变化图

本实验在0、15、25、35 和50 ℃五种环境温度下，让电池以BJDST、US06 工况进行放电，测量了电池放电过程中的电压、电流和电池表面温度，数据采样间隔为1 s。实验开始时，将电池以1C恒流充电至4.2 V，再以4.2 V 恒压充电，截止电流为0.1 A。然后，以不同工况对电池进行放电，放电的截止电压为3.4 V。将收集到的数据进行归一化处理，作为BidiGRU 的输入进行后续的SOC估计。

3 结果与讨论

3.1 BidiGRU 神经网络超参数的确定

将在五种温度下测得的BJDST 工况数据集作为训练集对BidiGRU 神经网络进行训练，以电池工作时的电压、电流、表面温度作为模型的输入，对应时刻的SOC作为输出。用US06工况来测试模型的泛化性能。该过程通过Python 3.7 Tensorflow Keras 框架实现，基于i7-5500U CPU 上运行。本文探究了不同BidiGRU 层神经元数对SOC估计结果的影响。文献[13]表明，BidiGRU 神经元数量的选取一般由经验选取，本文设定神经元数为30，是因为当神经元数设定值比30更大时，训练时间会变长，SOC估计结果并没有明显提高。神经网络的层数选择为1 层，是因为当层数增加时，SOC估计结果没有明显改善，训练时间会增加很多。详细的超参数设置见表1。

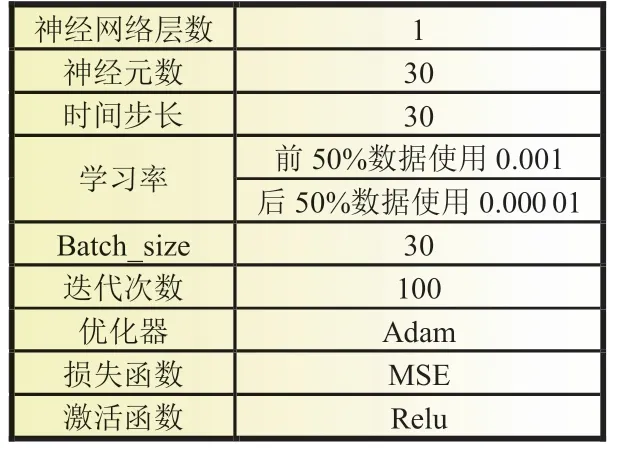
表1 BidiGRU 超参数设置

3.2 BidiGRU 神经网络估计SOC

在设置了BidiGRU 神经网络的超参数之后，使用梯度下降法对神经网络进行训练，其训练集损失变化、验证集损失变化如图5 所示。可以看到训练集损失可以下降到接近于0的水平，而验证集则在20 次迭代后明显上升，这是由于训练时出现了过拟合，采取了降低学习率的方式，将后50%的数据采用0.000 01 的学习率来进行训练，从而减小过拟合现象产生的影响。

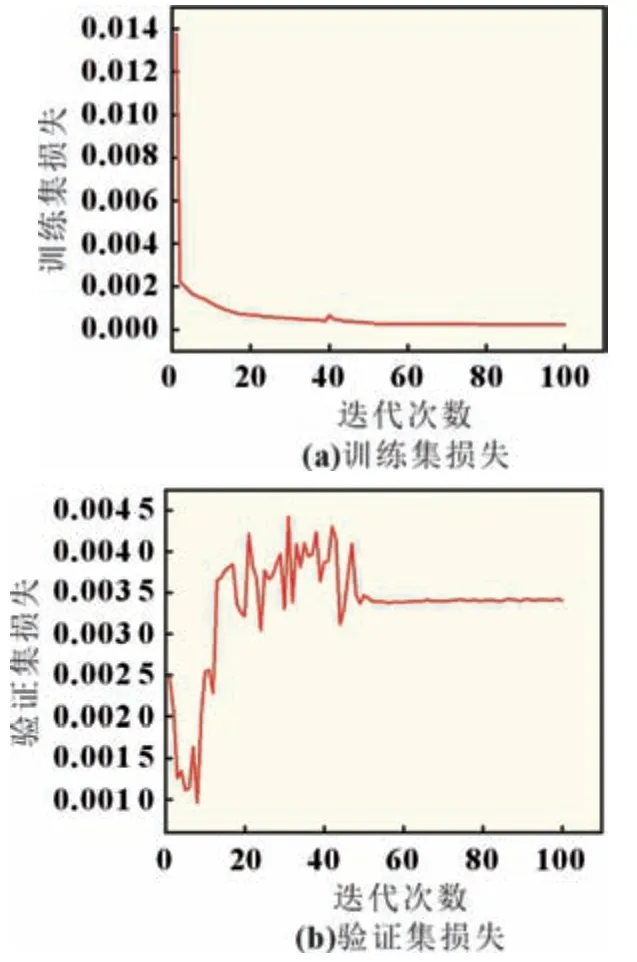
图5 训练集及验证集损失变化

取验证集损失最小的那一次迭代作为训练模型进行保存，接着使用0、15、25、35 和50 ℃下US06 工况进行测试。与此同时，我们在保持神经网络各超参数不变的情况下，将BidiGRU 神经网络换成了GRU 神经网络，并且用相同的数据进行训练，相同的数据进行测试，得到的SOC估计结果见图6。由图6 和表2 可知，在0 ℃下BidiGRU 的SOC估计精度较低，RMSE达到了3.66%，MAE达到了2.79%。35 ℃时估计结果最佳，RMSE可达到2.05%，MAE可达到1.58%。这主要是因为在低温下电池内部化学成分的活性较低，到截止电压时，往往只能放出很少的电量。由图6 可知，在0 ℃时，放电达到截止电压时，放出的容量是常温放电容量的一半。和其他温度下放电过程的SOC变化过程差异性较大，从而导致神经网络的训练效果不佳。在15、25、35 以及50 ℃时，BidiGRU 的估计精度相比于GRU 更高，其中15 ℃时，RMSE和MAE更是相差了近1.5%，尽管在0 ℃下BidiGRU 的估计精度不如GRU，但从整体来看，BidiGRU 在SOC估计上相比与GRU 仍更具有优势。

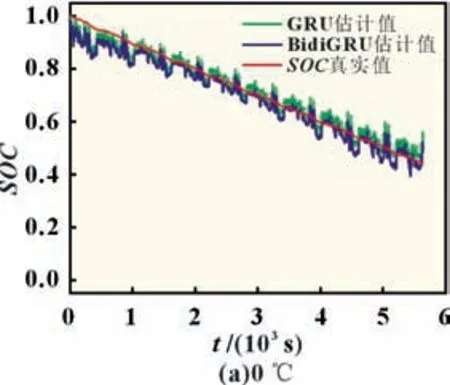
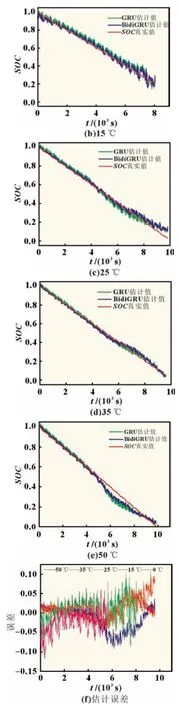
图6 US06工况SOC估计结果

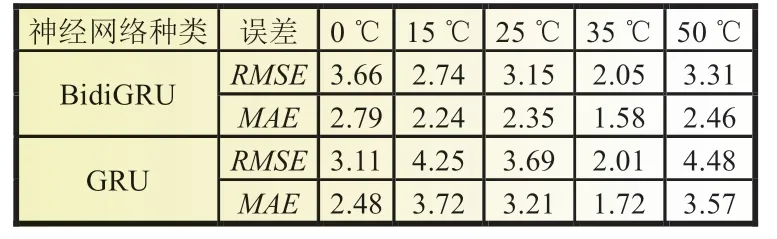
表2 US06 工况各循环神经网络对比 %

3.3 H∞滤波器优化BidiGRU 的SOC 估计结果

由于锂离子电池在不同温度下的放电容量差异性较大，BidiGRU 很难做到准确无误地估计每一种环境温度下的SOC，因此需要在BidiGRU 估计的SOC值的基础上，加以H∞滤波器进行优化，使得估计结果鲁棒性更好。使用H∞滤波器优化之后的SOC估计结果及其误差如图7 所示。通过和BidiGRU 估计得到的SOC比较可以发现，估计的精度得到了较大的提升，RMSE和MAE均降低到了0.5%以下，下降了2%以上。更加值得注意的是，在0 ℃下，经过H∞滤波器的优化之 后，RMSE和MAE由原来的3.66% 和2.79% 下降到了0.16%，达到了和其他温度下同样的精度，说明这种优化方法不依赖神经网络的估计精度，也说明H∞滤波器在系统统计特性未知时具有极佳的鲁棒性。表3 为US06 工况经H∞滤波优化后误差。

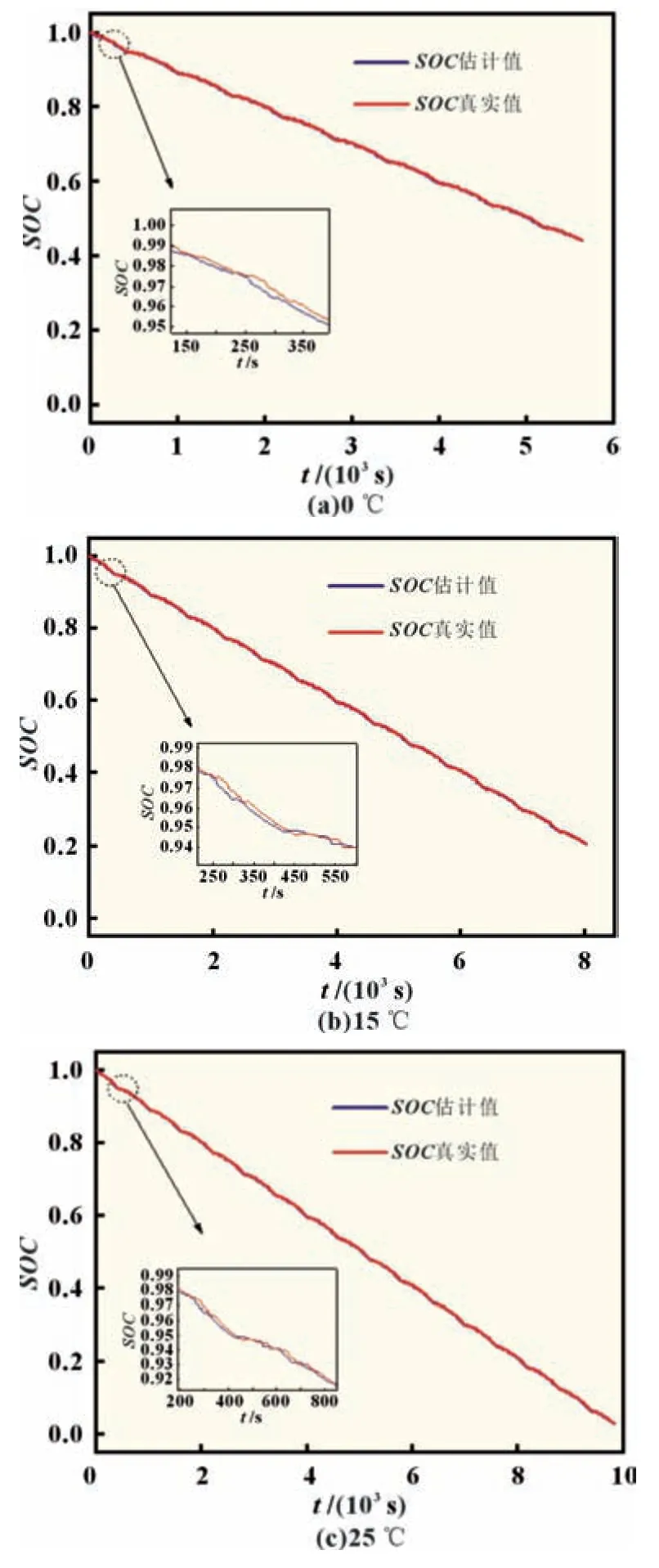
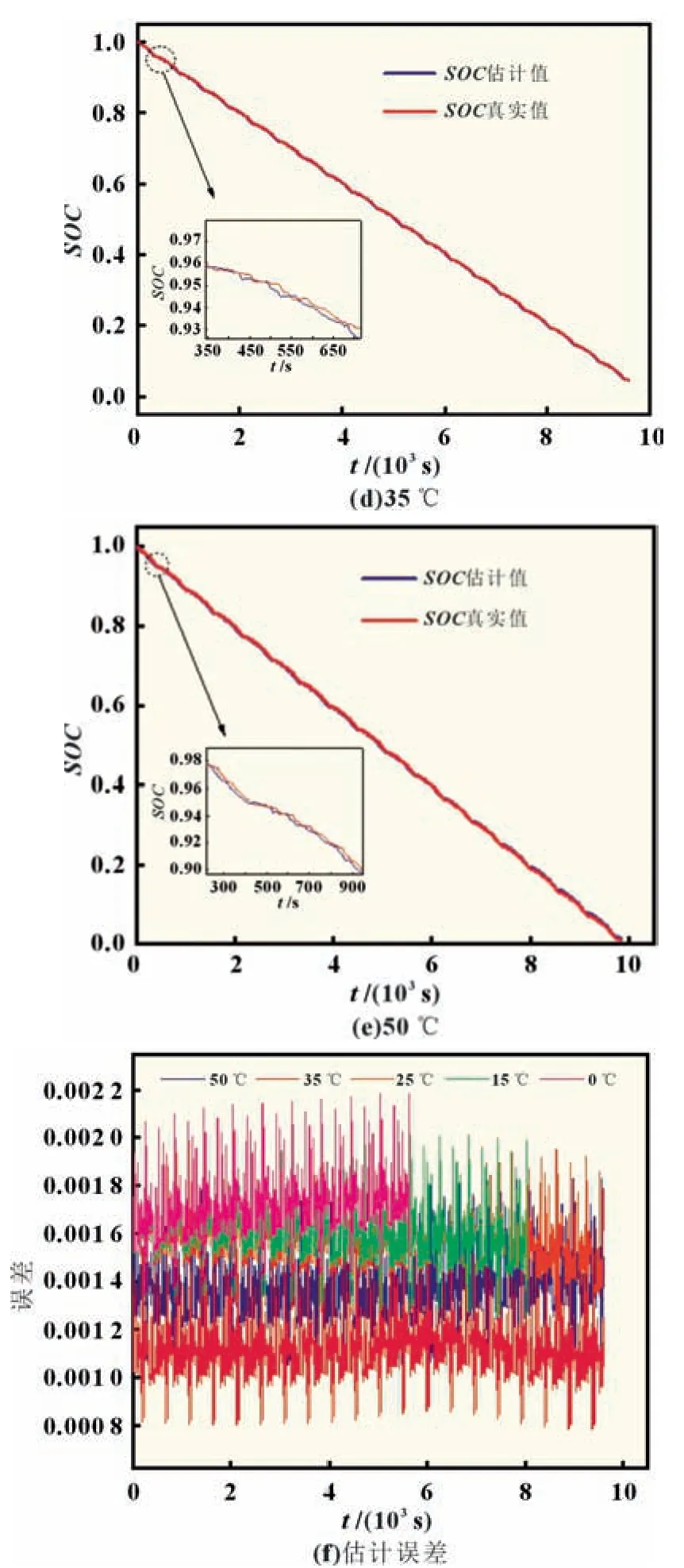
图7 US06工况经H∞滤波优化SOC估计结果

表3 US06 工况经H∞滤波优化后误差 %

4 结论

本文提出基于BidiGRU 神经网络和H∞滤波器估算锂离子电池SOC的复合方法。BidiGRU 神经网络以锂离子电池工作过程中的电压、电流、表面温度作为输入，输出每时刻的SOC，接着使用H∞滤波器对结果进行优化，使得其准确性和鲁棒性得到很大提升。实验探讨了0、15、25、35 和50 ℃五种环境温度下的电池放电过程中SOC的估计情况，用以上五种温度下的BJDST 工况作为训练集对BidiGRU 神经网络模型进行训练，用不同温度下的US06 工况进行测试，得到的SOC估计RMSE最低可达到2.05%，MAE最低可达到1.58%，但是在0 ℃下的估计误差较大，RMSE和MAE 可达3.69% 和2.79%。接着使用H∞滤波器BidiGRU 的SOC估计结果进行优化，得到最终的SOC估计值。结果表明：无论在何种环境下，该方法都能够做到准确的SOC实时估计，RMSE和MAE均能够达到0.17%以下。该方法是基于数据驱动的，不需要搭建复杂的等效电路，易于实现，因此该方法在SOC估计领域具有很大的应用前景。