海空协同的远海岛礁战储物资供给优化模型与算法

刘忠波，王淇娴，郑红星

(大连海事大学，交通运输工程学院，辽宁大连 116026)

0 引言

随着国家利益的不断拓展，南海海域的战略地位日益凸显，然而，该海域诸岛礁距离大陆较远，位置相对分散，若需保障战争初期的物资储备、战争后续补给以及应付突发事件的物资供应时，仅通过海上运输会出现运输周期过长，调配成本过高及难以高效支援的问题。为此，基于海空协同的战时战储物资供给优化研究可以满足战时或应急情况下的需求，对于提高我国远海作战能力，维护国家海洋权益具有极其重要的意义。

目前，国内外学者分析了战时战储物资调度体系的复杂性和建设的必要性[1]，并根据战储物资投送、交通网络建设的特点，提出改善建议等。关于物资补给过程，大多从物资分配及路径优化[2]角度结合“海运+冷藏班列+公路短驳”[3]等多式联运的方式进行研究。事实上，远海岛礁战储物资补给可以理解为海空协同运输的选址-路径问题，因此，在探究海上选址-路径问题的基础上[4]结合物资补给的特点，设立多目标优化予以解决更为贴切实际。但该问题在理论上是包含了中转基地选址、多阶段的航线设置及船型、机型的安排等的NP-Hard 问题，传统算法无法直接满足物资多阶段调度和海空协同运输中动态变换的求解需求，为此，可针对NSGA-II算法[5]进行改进，以期实现快速收敛，得到更优的解。

上述模型和方法为战时远海岛礁战储物资(简称：物资)供给研究提供了思路，但应进一步考虑该问题的特殊性：①南海岛礁地理位置的特殊性，物资需求地为远海岛礁，面积狭小且分散；②运输载体的特殊性，单依靠海运方式补给时间长，需利用海运和空运协同补给，且两者的运输载体在航速与载重量差异较大；③运输组织形式的特殊性，海运中多为往返运输。针对以上特殊性，本文分析远海岛礁的分布，兼顾考虑补给船、补给艇及运输直升机这3 种运输工具的特点，以中转基地选址，运输组织形式选择及航线配置等为优化内容，建立系统总时间最短和物资保障成本最低为目标的两阶段优化模型；并改进NSGA-II算法中拥挤度比较算子和精英保留策略。

1 模型分析

1.1 问题描述

南海海域因发生特殊事件进入战时状态，战役初期需大陆反应基地(简称：反应基地)补给。在实际供给行动中，受反应基地资源紧迫性、有限性的制约，需将多个反应基地作为物资供给点，形成以系统总时间最短和物资保障成本最低为目标的2EMLRP(两阶段双目标选址-路径问题)。

建模时基于以下假设：①各待补给岛的需求量已知，且多个反应基地的物资量可满足待补给岛的需求量；②海上通道均未受到破坏，可正常通行；③由于事件紧急性，直升机运送的物资均为消耗性物资；④补给艇和直升机的每个航次对其所服务待补给岛所需的物资进行均匀分配；⑤备选中转基地的泊位规格可以满足所有类型的补给船停靠要求。

1.2 符号说明

ο——反应基地，ο=1,2,…,O，O表示所有反应基地的数量；

p——备选中转基地编号，p=1,2,…,P，P表示所有备选中转基地的数量；

k——物资类型编号，k=1,2,…,K，K表示所有物资的种类；

s——补给船类型，s∈S，S表示补给船类型集合；

φ——第1 阶段往返航线编号，φ=1,2,…,n，n为决策变量，n∈ℕ，表示所有往返航线的数量；

φ——第1阶段循环航线编号，φ=1,2,…,m，m为决策变量，m∈ℕ，表示所有循环航线的数量；

Hφo——从反应基地ο出发编号为φ的循环航线上中转基地的个数；

——从反应基地ο出发编号为φ的循环航线上依次经过的第γ个中转基地的编号，1≤γ≤Hφο；

Qοk——反应基地ο存储物资类型为k的货物总量；

，，，vs、qs——分别表示s类型补给船的单位使用成本，单位运输成本，靠离泊时间，航行速度及最大载重吨；

，——分别表示货物类型为k的装卸成本和装卸时间；

dοp——反应基地ο至备选中转基地p的距离；

——备选中转基地p1到p2的距离，p1≠p2；

ip——备选中转基地p上的补给艇编号，ip=1,2,…,Ip，Ip表示备选中转基地p上的补给艇总数；

ℓip——补给艇ip的航次编号，ℓip=1,2,…,Lip，Lip为决策变量，Lip∈ℕ，表示补给艇ip的航次数量；

jp——备选中转基地p上的直升机编号，jp=1,2,…,Jp，Jp表示备选中转基地p上的直升机总数；

ςjp——直升机jp的航次编号，ςjp=1,2,…,Ejp，Ejp为决策变量，Ejp∈ℕ，表示直升机jp的航次数量；

T(endur)——直升机的最大续航时间；

——待补给岛的编号，表示所有待补给岛的数量；

——补给艇ip的第ℓip个航次中经过的待补给岛的个数；

——补给艇ip的第ℓip个航次中依次经过的第τ个待补给岛的编号，1≤τ≤；

——直升机jp的第ςjp个航次中经过的待补给岛的个数；

——直升机jp的第ςjp个航次中依次经过的第σ个待补给岛的编号，1≤σ≤；

——待补给岛p对物资类型为k的货物需求量；

——中转基地p到待补给岛的距离；

——待补给岛到待补给岛之 间 的距离；

c(const)，c(ship)，v(ship)，q(s hip)——分别表示补给艇的单位使用成本、单位运输成本、航行速度及最大载重吨；

，c(p lane)，v(p lane)，q(p lane)——分别表示直升机的单位使用成本、单位运输成本、飞行速度及最大载重吨；

M——无穷大的数：

xp——0-1 决策变量，若备选中转基地p选为中转基地进行物资中转，xp=1，否则，xp=0；

yφs——0-1 决策变量，当第1 阶段往返航线φ配置船型为s时，yφs=1，否则，yφs=0；

zφs——0-1 决策变量，当第1 阶段循环航线φ配置船型为s时，zφs=1，否则，zφs=0；

rφο——0-1 决策变量，若应急基地ο在第1 阶段往返航线φ内时，rφο=1，否则，rφο=0；

uφο——0-1 决策变量，若应急基地ο在第1 阶段循环航线φ内时，uφο=1，否则，uφο=0；

aφp——0-1决策变量，若备选中转基地p在第1阶段往返航线φ内时，aφp=1，否则，aφp=0；

——0-1决策变量，若备选中转基地p在第1 阶段循环航线φ的第γ个位置时，1，否则，0，1≤γ≤Hφο；

——0-1 决策变量，若待补给岛在补给艇ip的航次中第τ个位置时，1，否则，

——0-1决策变量，若待补给岛在直升机jp的航次中第σ个位置时，1，否则，

ηpk——整数变量，表示第k种货物运送到备选中心岛p的实际送达量；

——补给艇ip的航次中在待补给岛所卸下的第k种货物的数量；

——直升机jp的航次中在待补给岛所卸下的第k种货物的数量。

1.3 第1阶段计算模型

物资供给的第1 阶段是将物资从反应基地运送至中转基地，由于运送物资量大，且反应基地与中转基地之间的距离较远，该阶段大多由补给船来承担运输任务。

1.3.1 第1阶段时间计算模型

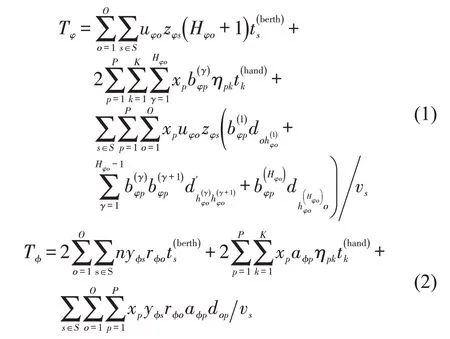
式(1)和式(2)分别表示循环航线φ和往返航线φ中补给船的运行时间。其中，第1 部分表示靠离泊时间，第2 部分表示装卸时间，第3 部表示航行时间。

1.3.2 第1阶段成本计算模型

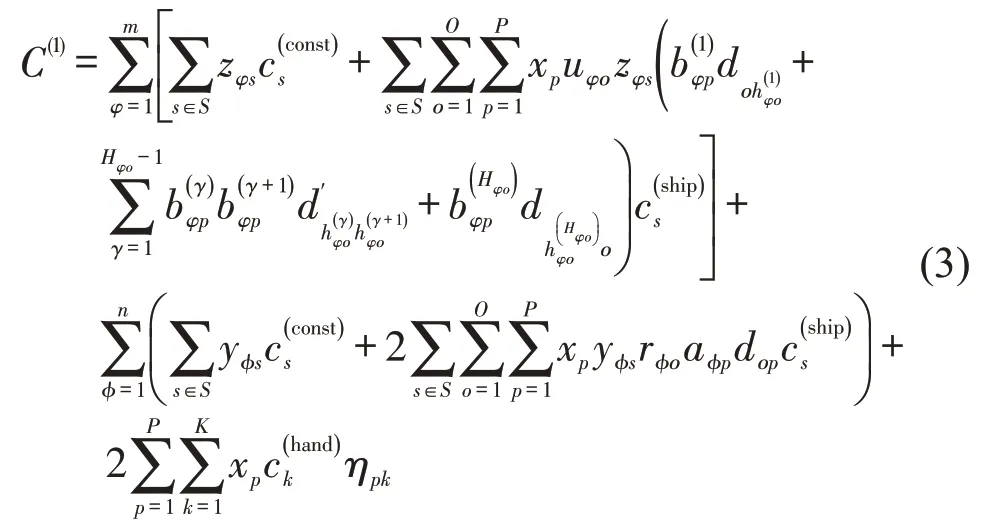
式(3)表示所有补给船的运行成本，其中，第1部分表示循环航线φ中所有补给船的运行成本，第2部分表示往返航线φ中所有补给船的运行成本，第3部分表示所有补给船的装卸成本。

1.4 第2阶段计算模型

第2阶段的运输过程中，中转基地到各待补给岛间距离较近，因而，可以使用补给艇和直升机协同运输的组织形式，将物资快速、高效且均匀地运至各个待补给岛。

1.4.1 第2阶段时间计算模型

式(4)表示补给艇的运行时间，其中，第1 部分表示靠离泊时间，第2部分表示装卸时间，第3部分表示航行时间；式(5)表示直升机的运行时间，其中，第1部分表示装卸时间，第2部分表示航行时间。

1.4.2 第2阶段成本计算模型

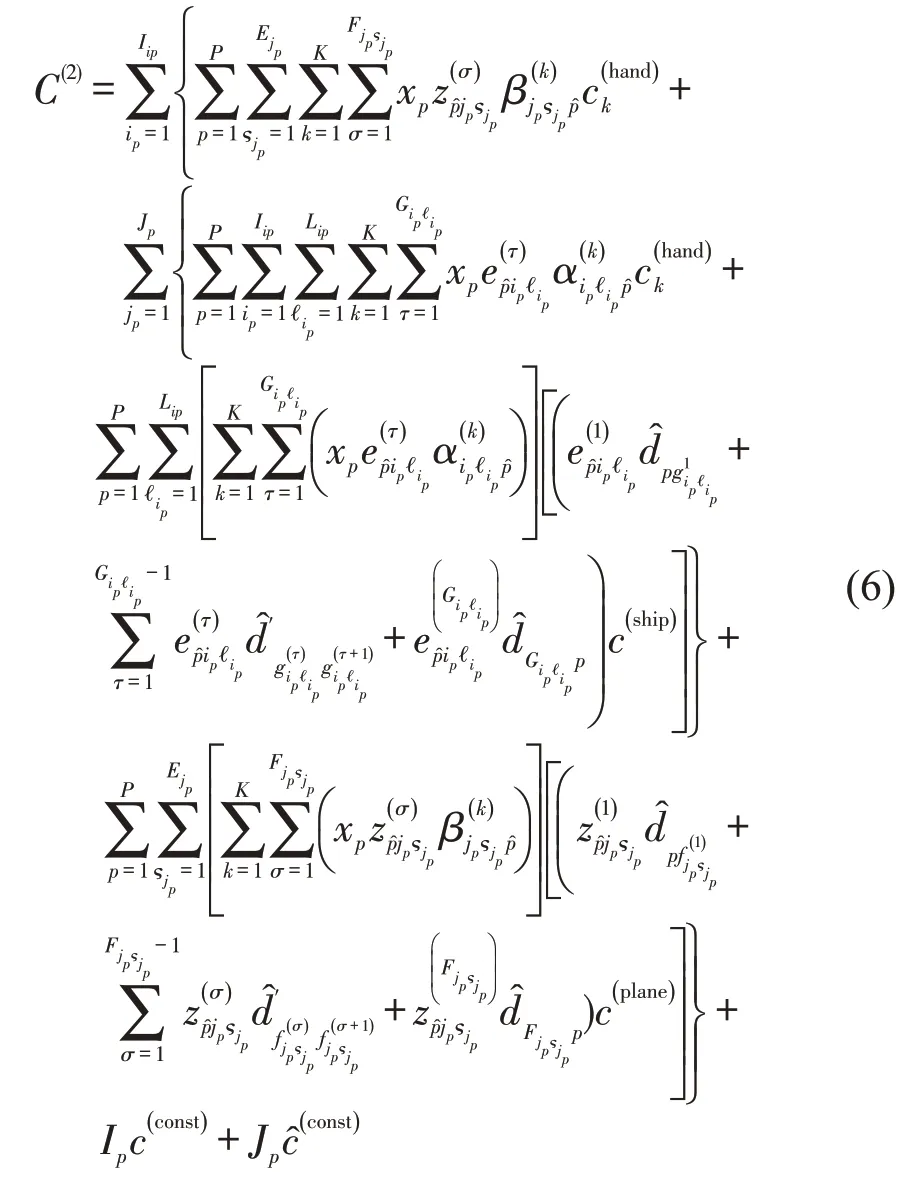
式(6)表示第2 阶段补给艇和直升机的运行成本，其中，第1 部分表示补给艇和直升机的装卸成本，第2部分表示补给艇和直升机的航行成本，第3部分和第4 部分分别表示补给艇和直升机的使用成本。

1.5 模型整合

综合以上各部分，以系统总时间最短和物资保障成本最低为目标的模型为

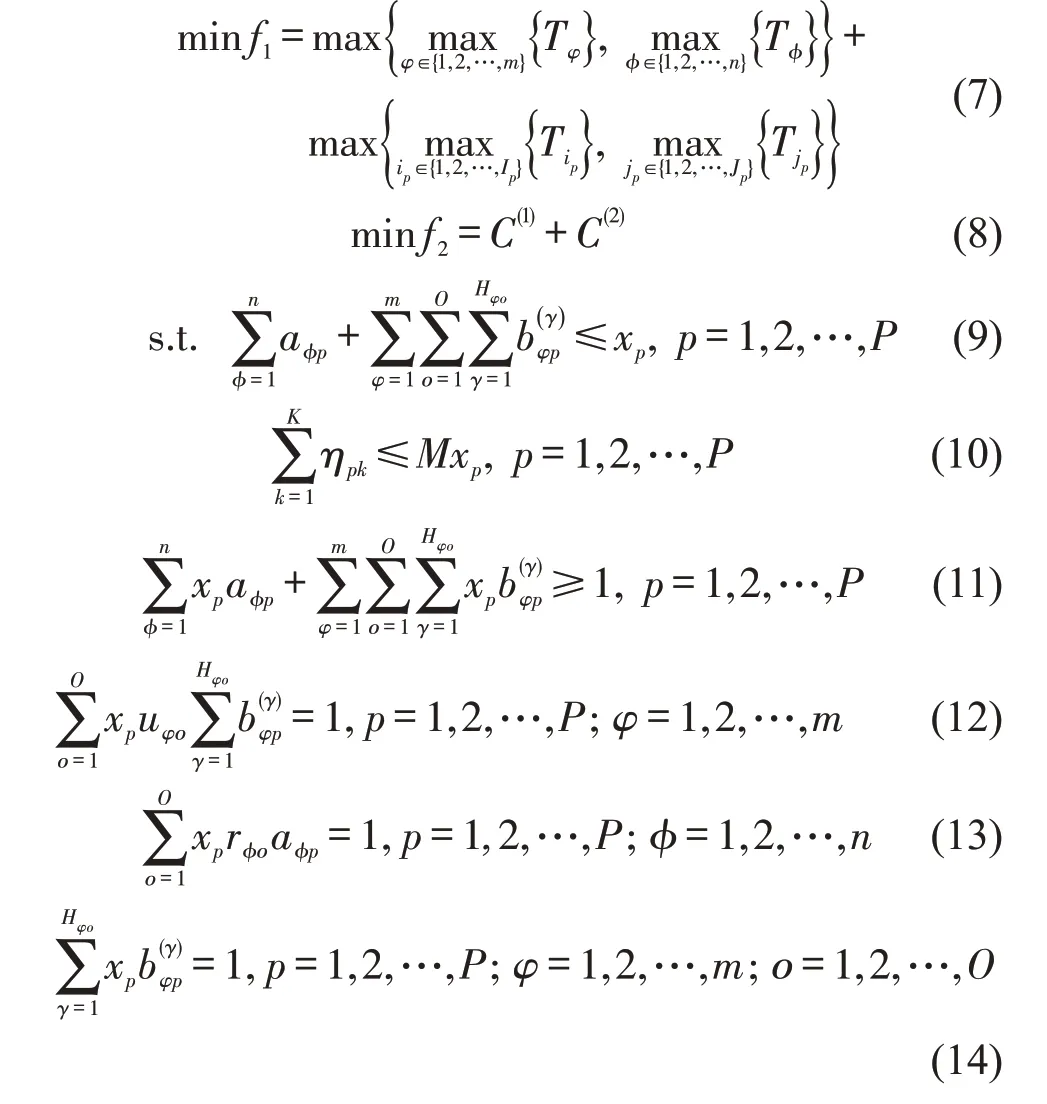
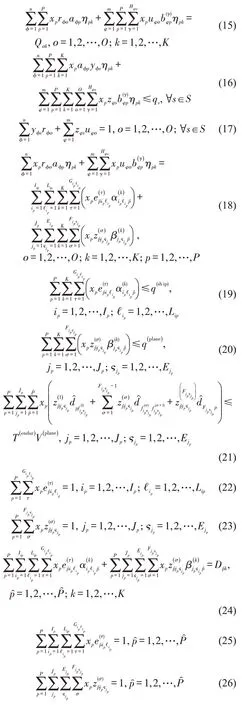
式(7)表示系统总时间最短；式(8)表示物资保障成本最低；式(9)表示只能给中转基地分配相应运输航线；式(10)表示只有中转基地才可以接收从反应基地运送的物资进行货物中转；式(11)表示每个中转基地至少被分到一个航线内；式(12)和式(13)表示循环和往返航线中，每个中转基地只能由1个反应基地进行物资运送；式(14)表示每条循环航线仅服务某待补给岛1 次；式(15)表示反应基地O存储物资类型为k的货物总量等于其运往中转基地持有物资类型为k的货物总量；式(16)表示补给船从反应基地向中转基地运送的物资总量之和不超过第1 阶段不同船型的补给船载重量之和；式(17)表示单个反应基地的单次航线只能属于1 种运输组织形式(航线类型)；式(18)表示中转基地各物资的运出量之和与其运送到相应待补给岛的总量之和相等；式(19)和式(20)表示每艘补给艇和直升机单次运送的物资总量之和小于补给艇和直升机的最大载重量；式(21)表示直升机续航能力限制；式(22)和式(23)表示每艘补给艇和每架直升机的单次航线只能服务某待补给岛1 次；式(24)表示中转基地对各类物资的总持有量等于其运往各待补给岛对各类物资的需求量总和；式(25)和式(26)表示每个待补给岛只能由1个中转基地服务。

2 算法设计

通过以上分析可知，本文决策变量和约束条件众多且复杂，基于此，提出改进的NSGA-II算法，同时使用双层并行搜索的方式来解决。核心思想是：上层染色体对中转基地选址、反应基地的航线配置及补给船类型编码，下层染色体在上层染色体选择结果的基础上配置中转基地和待补给岛间补给艇和直升机的航线，通过上、下层间的交互和算法进化得到最终方案。

2.1 遗传算法

2.1.1 染色体编码

为求解本文问题，需先对上、下两阶段的染色体分别进行编码。如图1所示，第1 阶段的染色体编码需构造3 个基因段，基因段1 表示备选中转基地的编号；基因段2中1和2表示反应基地的编号，0 表示该备选中转基地未被选为中转基地；基因段3中每3个基因为一组，表示2个反应基地，每组基因表示每个反应基地配置的补给船类型，其中，第1位基因座表示A类型的补给船，第2位表示B类型，第3 位基因座表示C 类型，0 表示不配置，1 表示配置相应类型补给船。如图2所示，在第2 阶段的染色体编码中，染色体表示中转基地至待补给岛的运输方案，基因段1表示待补给岛的编号；基因段2表示中转基地的编号。

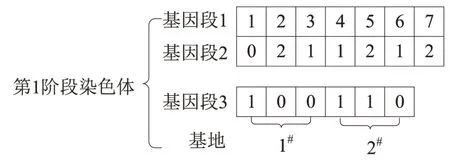
图1 第1阶段染色体编码Fig.1 Chromosome coding of first stage

图2 第2阶段染色体编码Fig.2 Chromosome coding of second stage

2.1.2 算法及其改进

(1)拥挤度比较算子的改进

NSGA-II 算法中非边界点的拥挤距离计算公式为

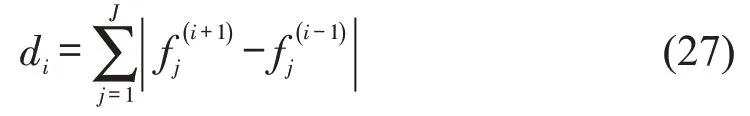
式中：di——第i个非支配解的拥挤距离；

——第i+1 个非支配解的第j个目标函数值。

种群内个体分布实例如图3和图4所示。

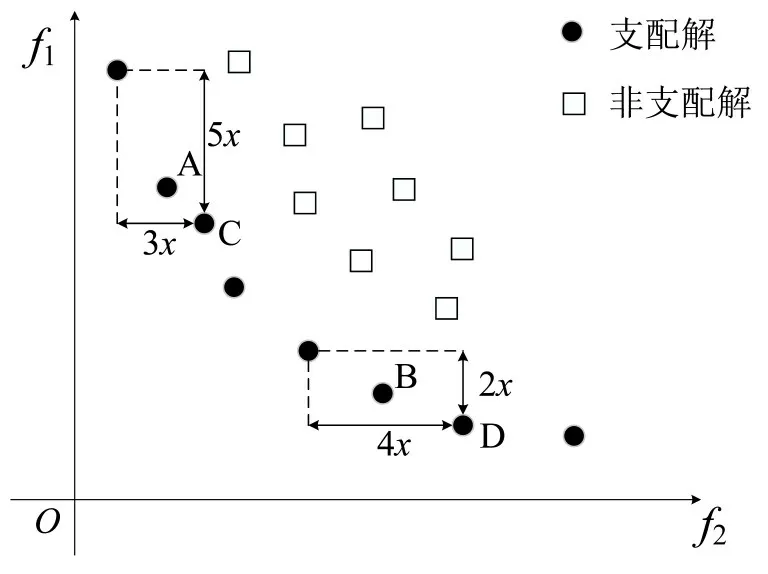
图3 种群内个体分布实例Fig.3 Example diagram of individual distribution in population

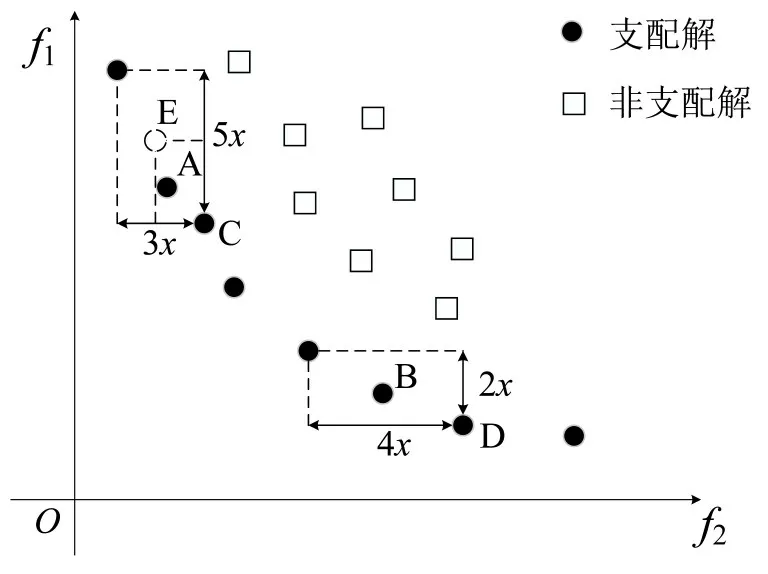
图4 种群内个体分布实例Fig.4 Example diagram of individual distribution in population

根据式(27)可以计算，图3中A 点和B 点的拥挤距离分别为8x和6x，(x为单位长度)即B点比A点更加拥挤，但直观发现A点比B点更拥挤。根据NSGA-II的算法规则会删除B点，若在交叉过程中A 点与C 点交叉，则会造成个体子代与父代相似，进而导致算法收敛到某一局部最优解。

造成上述问题的原因在于个体间的拥挤距离与分散程度的度量方式存在偏差，拥挤距离大的个体其分散程度不一定小。为此，本文将个体i与其前后相邻的个体i+1 和i-1 间的距离也考虑在内，形成新的拥挤距离计算式为

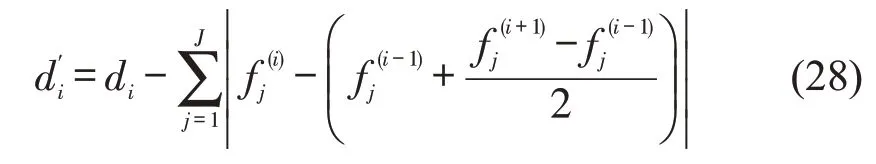
式(28)在传统拥挤距离计算基础上减去个体i与其前、后相邻个体i+1 和i-1 间的距离，如图4所示，A 点新的拥挤距离等于A点的拥挤距离减A点与E点间的拥挤距离，该差值衡量的是个体A与其最理想位置E间的距离，且该值越小表示A点与其前、后相邻点间的均匀性越大。

(2)精英保留策略的改进

本文提出一种自适应分级精英保留策略，具体操作为：从非支配等级低的解集中选择较多个体，从非支配等级高的解集中选择较少个体，使算法在进化过程中根据非支配集的规模大小逐步提高种群中精英个体保留的规模，使其在前期保持种群的多样性，在后期尽快收敛到帕累托前沿。具体选取公式为式中：i——支配层级编号；

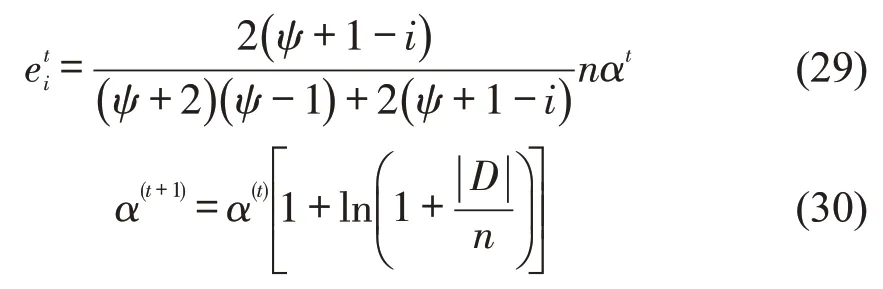
t——迭代次数；

——第t次迭代时在第i个非支配层级选取的个体数目；

α(t)——第t代非支配个体选择数量的自适应权重；

ψ——最大非支配层级；

n——种群规模大小；

|D|——非支配解的数量。

2.2 计算步骤

利用算法求解后，可得到一系列Pareto 非劣解，考虑决策者的偏好不同，如要寻求满意解，可根据“性价比”法[6]进行筛选。本文旨在选择兼顾考虑系统总时间和物资保障成本两个目标的满意解，可选择两个优化目标偏向度最小的点所对应的解作为满意解。综上，可得具体的计算流程如图5所示。

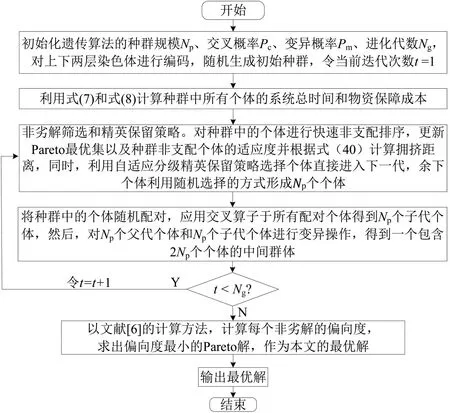
图5 计算流程Fig.5 Calculation flow chart

3 算例分析

3.1 基本数据

现以向我国南海岛礁供给物资为例，假设距离南海岛礁最近且有物资储备量的反应基地有2个，其坐标及物资存储量如表1所示，其中，①类物资主要是医疗和生活用品，②类物资主要是弹药和材料。

表1 反应基地坐标及物资存储量Table 1 Coordinates and material storage of reaction base

备选中转基地的岛礁有7 个，如表2所示，各备选中转基地中均有2 艘补给艇和1 架直升机。

表2 各备选中转基地的坐标Table 2 Coordinates of each standby transfer base

补给船、补给艇及直升机的相关信息如表3所示，其中，直升机只能运输①类物资，补给船和补给艇可以运输①类和②类物资。各待补给岛的坐标和物资需求量如表4所示。

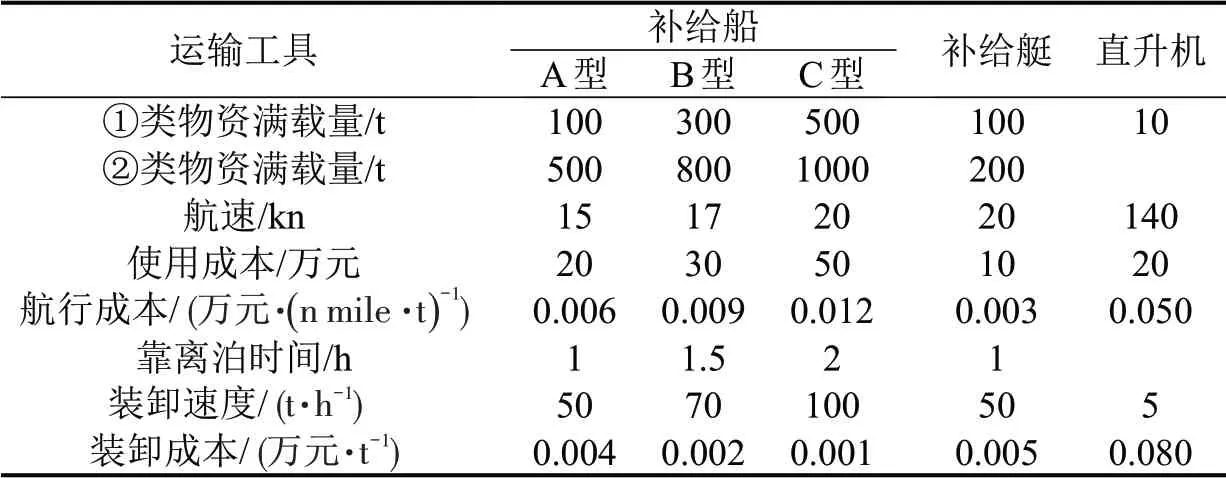
表3 补给船、补给艇和直升机参数信息Table 3 Information on supply ships,supply boats and helicopters

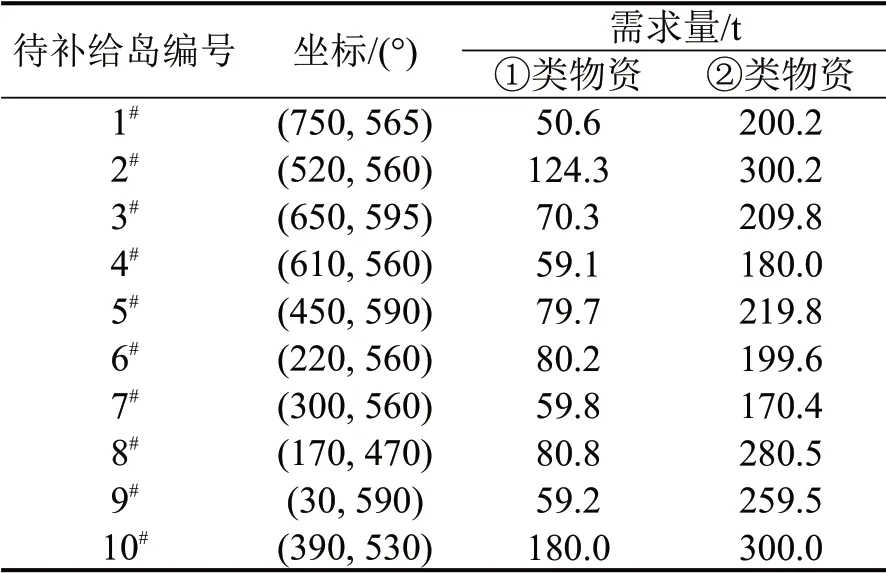
表4 待补给岛坐标和需求量Table 4 Coordinates and demand of island to be replenished

3.2 计算结果

本文使用Python语言编程，设定改进NSGA-II算法的种群数量NP=30，交叉概率Pc=0.6，变异概率Pm=0.02，迭代次数Ng=1000 次。经计算得到的Pareto 非劣解18 个，如图6所示；利用“性价比”法求得解7#的偏向度最小，如图7所示，则该解为满意解，其目标函数值分别为9.43 d 和1010.84 万元。

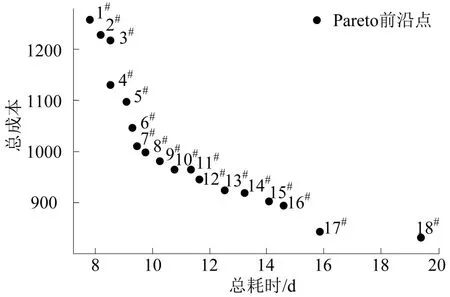
图6 求解优化模型得到的Pareto前沿Fig.6 Pareto frontier obtained by solving optimization model

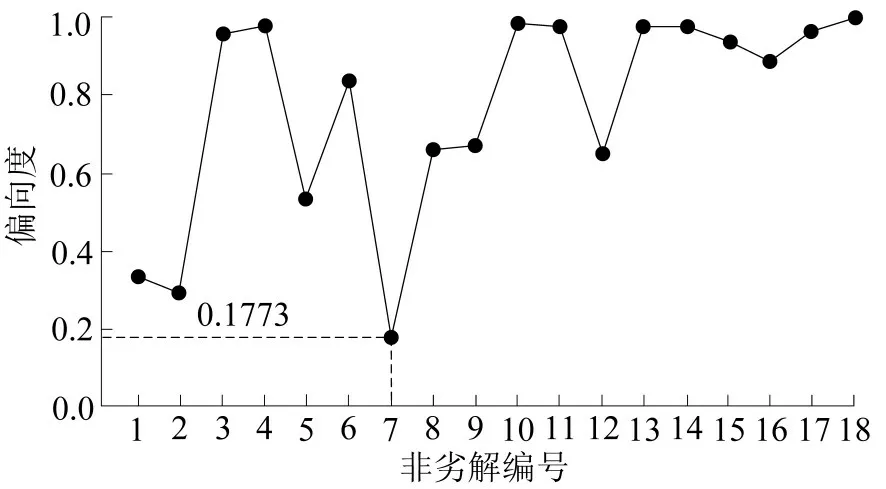
图7 Pareto非劣解的偏向度Fig.7 Skewness of Pareto non inferior solution

最优方案中选择备选中转基地2#、3#、4#、6#、7#作为中转基地，具体的运输安排如表5～表7所示。物资供给运输方案如图8所示。

表5 反应基地至中转基地的补给船运输方案Table 5 Supply ship transportation scheme from reaction base to transfer base

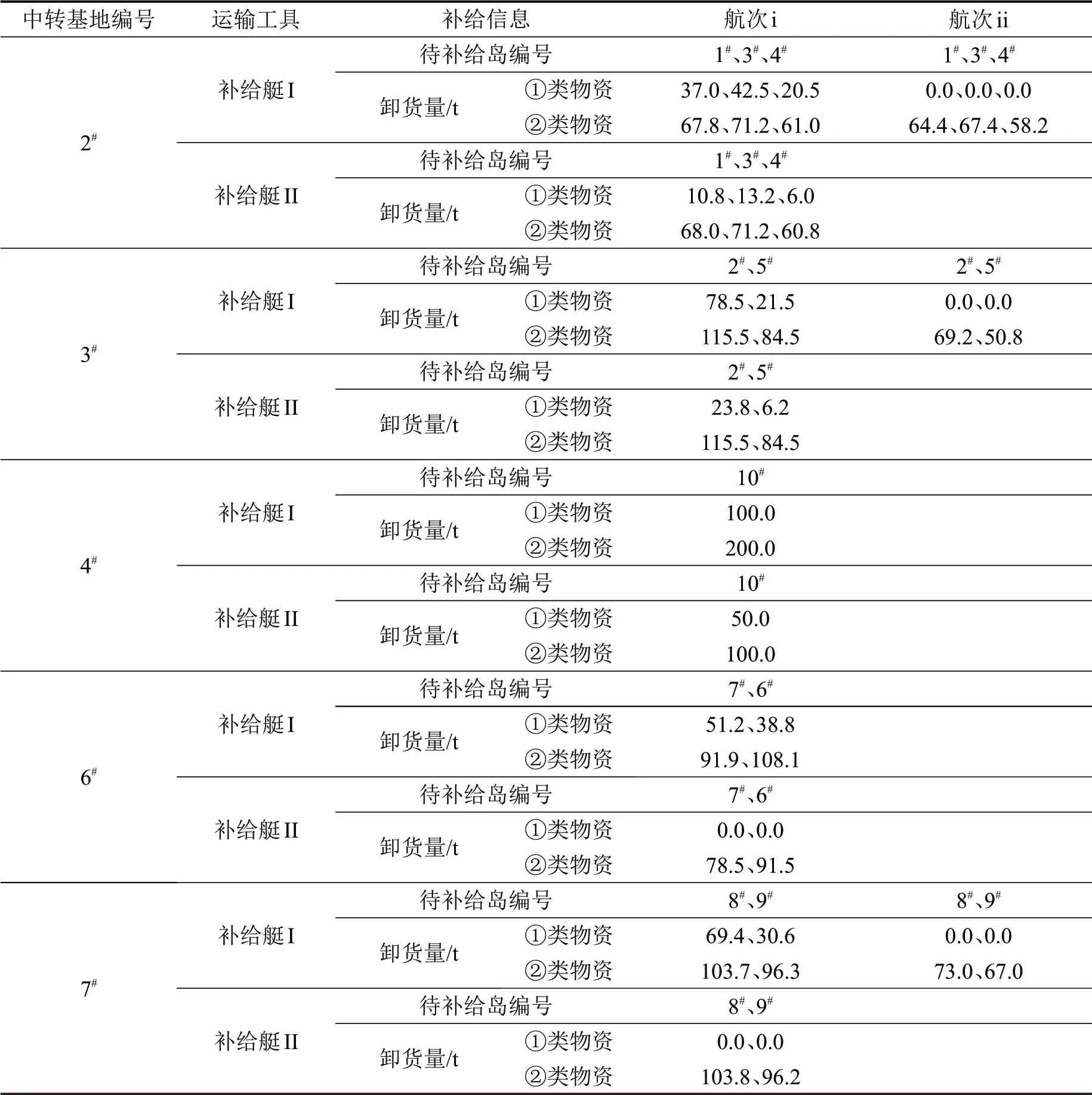
表7 中转基地的补给艇运输方案Table 7 Supply boat transportation scheme of transfer base

3.3 算例分析

3.3.1 海空协同模型最优方案分析

如图8所示，中转基地的地理位置分布较为均匀，数量居中，既能有效衔接上、下节点实现高效运输，同时，在经济性上也达到相对满意。第1 阶段的运输中，由于补给船的载重量较大，“三角形”式的循环运输会比往返运输更加高效；在第2阶段的运输中，为使各类物资均匀的运送至待补给岛，补给艇在到达待补给岛前，直升机要对航线内的待补给岛持续补给物资，直至补给艇将所需的全部物资送达某待补给岛时才停止对该岛的补给，且方案优化后，各中转基地服务的待补给岛数量在1～3 之间，也恰好避免数量过多而引起物资分配不均匀的情况，符合最优方案的要求。

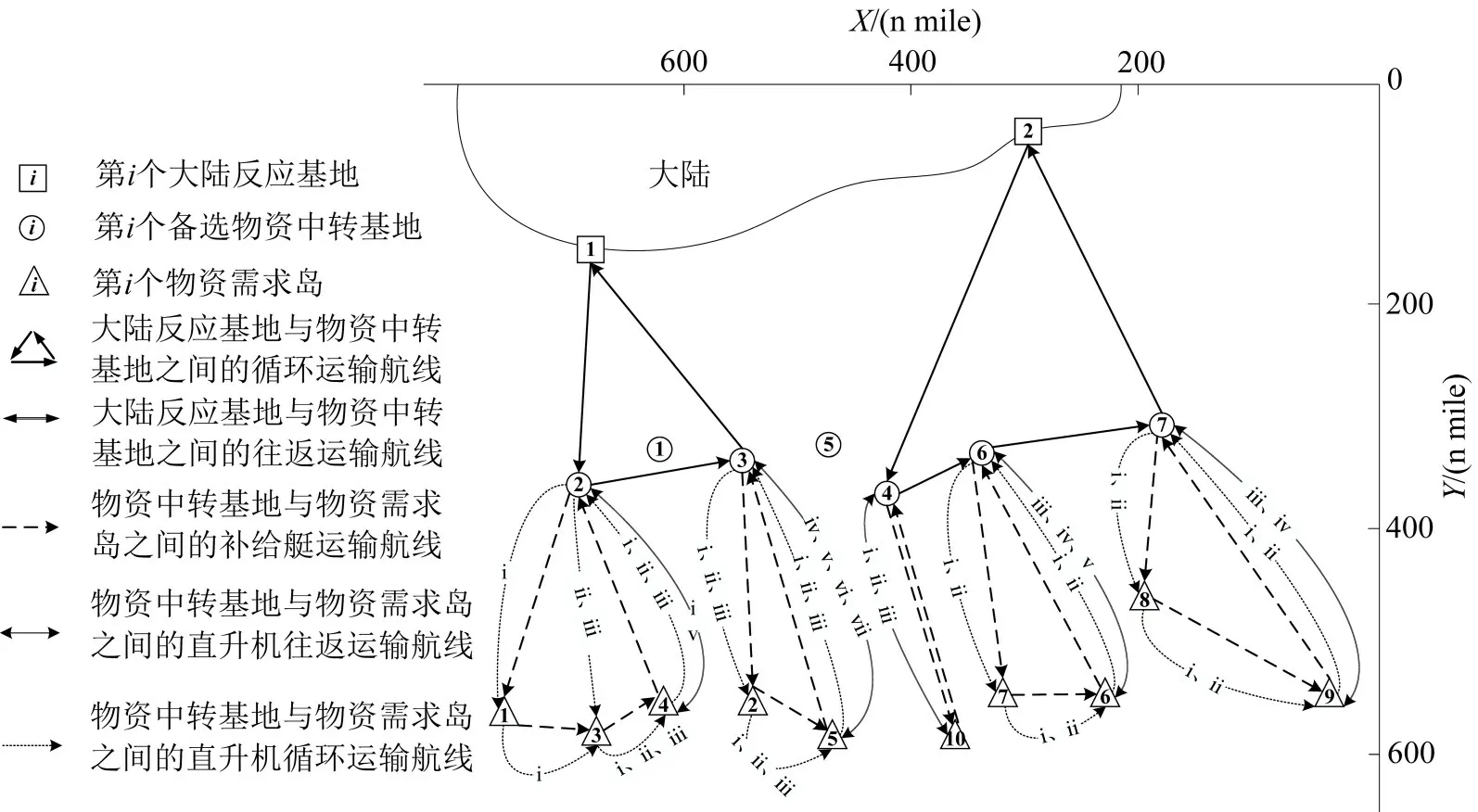
图8 海空协同物资供给运输方案图Fig.8 Plan of sea air coordinated material supply and transportation

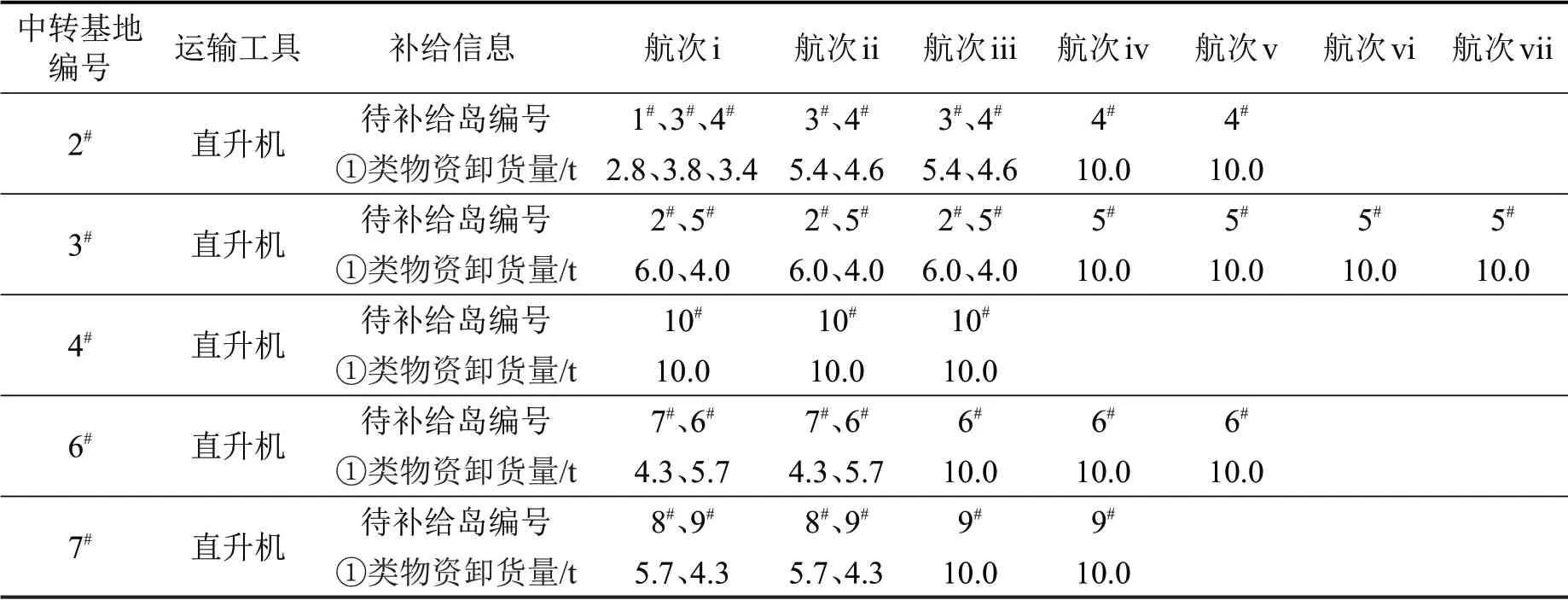
表6 中转基地的直升机运输方案Table 6 Helicopter transportation scheme of transfer base

3.3.2 海空协同模型与全海运模型对比分析

为说明海空协同运输的优越性，将本文模型改为全程海运的方式，利用基本数据进行计算，将得到的结果与海空协同的结果进行对比，如图9所示。

从图9可发现，求解海空协同模型得到的Pareto 前沿点分布于左上区域，求解全海运模型得到的Pareto前沿点分布于右下区域，说明海空协同运输下系统总时间比全程海运更具优势，但物资保障成本略高。通过计算总成本与总耗时间的平均变率[6]可以发现，海空协同模型的平均变率为489.99，说明时间每增加1 d，成本平均减少489.99 万元；全海运的平均变率仅为135.74，显然，海空协同的方案更优。

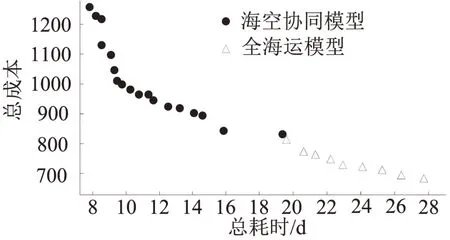
图9 Pareto前沿点对比Fig.9 Pareto frontier comparison chart

如图8所示，求得全海运模型的满意解与海空协同模型的满意解对比发现，相对于全海运模型，海空协同模型的总成本增加了22.27%，但总时间降低了53.15%。另外，通过计算两种模型满意解中待补给岛第1次获得补给物资的平均时间可知，海空协同模型为4.89 d，全海运为7.84 d；海空协同下，各待补给岛收到第1 批物资时间相差最多为0.04 d，而全海运为2.3 d，海空协同优势明显。在物资补给过程中，存在某些需求量较小但更为紧急的物资，利用直升机可以优先运送此类物资，可为补给艇后续运输起到前期保障与缓冲的作用。若采用全海运则无法满足此类要求，首先接受第1批物资补给的岛礁与最后接受第1 批物资补给的岛礁时间相差过大，难以满足实际要求。

表8 方案对比表Table 8 Scheme comparison table

3.4 算法对比分析

为分析本文算法的有效性，对基本数据中反应基地物资总量和待补给岛需求量均扩大1 倍后得到2组算例进行计算，2组算例均运行10次，结果如图10所示。算法评价指标采用间距指标SP[7]和最大分散度MSP[8]，对比结果如表9和表10所示。其中，间距指标越小，最大分散度越大，则求得的Pareto解分布性越好。

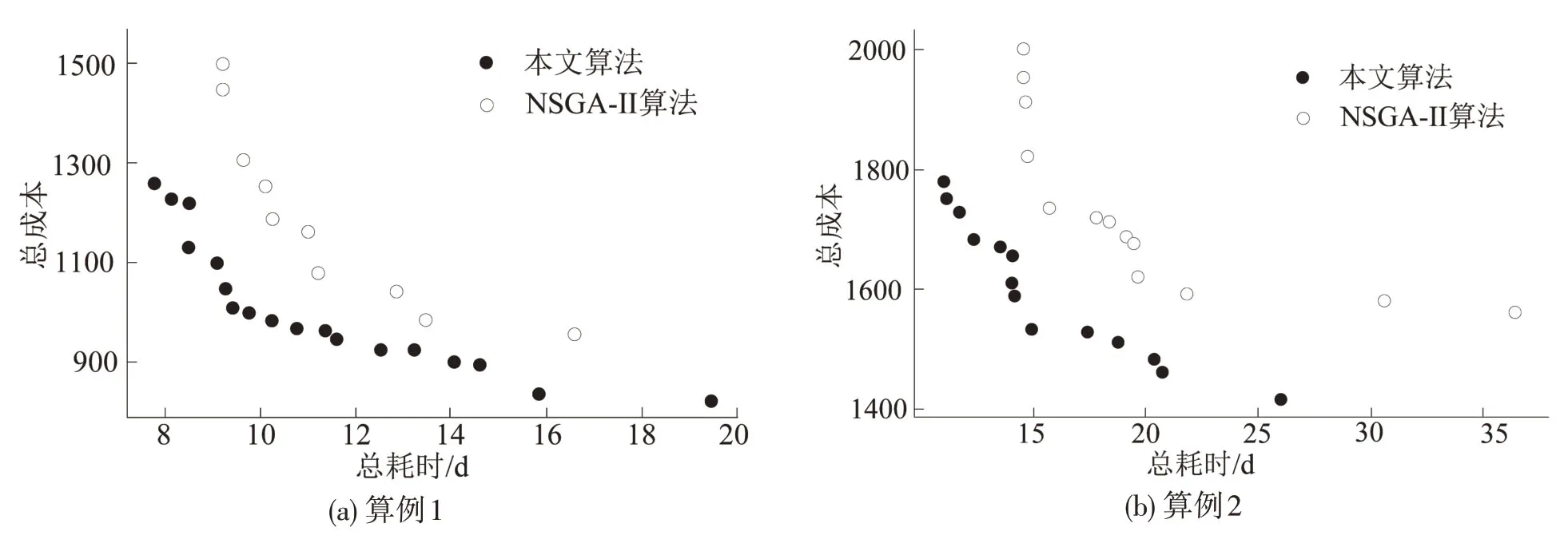
图10 算法对比Fig.10 Algorithm comparison diagram

表9 算法改进前、后SP值对比Table 9 Comparison of SP values before and after algorithm improvement

表10 算法改进前、后MSP值对比Table 10 Comparison of MSP values before and after algorithm improvement

对比结果显示：本文算法求得的SP 指标在平均值上改进幅度为22.17%～23.56%；在最小值上改进幅度为10.79%～16.23%。MSP 指标在平均值上改进幅度为10.74%～26.29%；在最大值上改进幅度为9.74%～14.48%。表明本文算法求得的解集均匀性较好。同时，从图10也可看出，本文算法求得的帕累托解集更接近于真实帕累托前沿。

综上所述，本文最终方案在时间上可以满足战储物资投送的紧迫性要求，成本上相比于时间稍短的其他方案有大幅度降低，可以在满足时间约束的同时最大限度节约成本，本文提出的改进NSGA-II算法获得解的优化结果更好，且具有良好的分布性。

4 结论

本文讨论了海空协同下战储物资的战时供给优化问题，研究结果表明：

(1)本文利用“性价比法”选择的最终方案比3.2 节中解1#的时间增加17%，成本却降低26%；比解18#的时间降低58%，成本仅增加31%。

(2)海空协同模式下物资补给时间比纯海运降低53.15%，成本仅增加22.27%；海空协同模式下，送达第1 批待补给物资的平均时间比全海运模式缩短了2.95 d，全海运下，各待补给岛收到第1批物资的平均时间差值比海空协同下多2.26 d，海空协同下，时间每增加1 d 成本降低幅度为纯海运的3.6 倍。

(3)通过选取放大规模的算例与传统NSGA-II算法对比可知：本文算法求得的SP 指标在平均值上改进幅度为22.17%～23.56%，在最小值上改进幅度为10.79%～16.23%；MSP指标在平均值上改进幅度为10.74%～26.29%，在最大值上改进幅度为9.74%～14.48%。