不确定交通需求下交叉口信号配时区间优化模型

陈小红，蓝秋雨

(广西大学，数学与信息科学学院，南宁 530004)

0 引言

交通系统是典型的不确定性系统，交通流的不确定性严重扰乱城市交通管理与控制，直接影响交通控制参数设置与控制效果评价。交通数据是控制策略制定和控制算法设计的基础，决定了交通控制系统的适用性、可靠性及先进性[1]，是控制系统实现对城市交通最佳控制的关键基础。随着交通数据采集途径和方法的不断革新，交通控制已逐步转向面向数据驱动的智能控制，快速响应交通流的变化和预测控制效果，从而处理交通流的不确定性[2]。刘红红等[2]针对交通流的时变性与动态性，提出分布式多智能体控制；温惠英等[3]提出了一种基于学习的模糊交通控制方法；LIANG等[4]提出了一种基于网联车技术的以公平与效率为目标的单交叉口信号控制方法。此类方法主要围绕获取及处理实时数据的手段和方法，解决交通系统的时变性与动态性，并未从本质上反映交通流到达规律的变化。TONG 等[5]针对过饱和交叉口，提出了使车均延误期望最小的信号配时参数随机优化模型；WADA 等[6]基于变分理论，提出随机需求下干道协调控制优化模型。模糊优化与随机优化虽然在一定程度上弥补了精确数学模型的缺陷，但在实际工程中，不确定参数的概率分布函数和隶属度函数的确定需采集大量实时交通数据，成本高、难度大，且对于由检测环境差异导致的数据误差和道路上不同类型交通流间的交叉干扰等，不管分布函数或隶属度函数怎样假设，都无法准确刻画实际交通流频率。为有效解决交通需求波动，张萌萌等[7]提出基于延误均值与标准差的交叉口信号配时鲁棒优化模型；YIN[8]提出了过饱和状态下，基于情景的交叉口定时控制鲁棒优化模型；赵靖等[9]针对排阵式交叉口，考虑交通需求、饱和流率及运行车速这3 个客观因素的波动，构建基于情景的几何设计和交通控制协同鲁棒优化等。鲁棒优化方法已广泛地应用到干线协调控制和网络控制，但鲁棒优化模型是一个NP难问题，需要确定不确定集与其等价模型，并进行参数估计，模型敏感且计算量大，易出现过度保守的情况。

近年来，随着区间数越来越多地被用来描述参数的不确定性，区间优化作为非概率不确定性优化的有效处理方法，已发展成为继随机优化和模糊优化的第三大类不确定优化方法，在诸多实际工程领域展现出较强的应用价值。在交通控制优化中，卢凯等[10]引入区间集对分析方法，研究面向速度区间的干道绿波协调控制方案，该方法主要讨论了面向速度区间的干道协调控制方案，但是并未直接考虑交通流量和饱和流率等关键基础参数的不确定性对交通信号控制系统的影响。有鉴于此，本文针对不确定交通需求下交叉口混合交通信号配时优化问题，利用区间数理论分析交通量和饱和流率两个不确定参数，构建交通控制信号配时参数区间优化模型，响应交通流的波动对交通控制系统的影响，提高控制方案的适应性和可靠性。

1 信号配时参数区间优化模型

1.1 混合饱和流率区间测算

饱和流率是设置配时方案和确定服务水平的重要参数，其大小受车辆构成类型、车道性质、车辆间相互关系及非机动车干扰等影响，这些因素与交通流实时状态有着密切关系，表现出较强的不确定性[11]。关于其测算的研究已取得一定的成果，例如，美国通行能力手册(HCM2010)[12]提出的在理想饱和车头时距的基础上乘以各种影响因素的折减系数；王殿海等[11]提出的面向数据驱动的实时估计方法，能较好地适用于实时交通信号控制，但未考虑非机动车的干扰。本文修正HCM2010中提出的混合交通饱和流率计算公式，讨论混合交通量为区间数时，饱和流率区间确定方法，描述混合交通饱和流率不确定参数。

纵观饱和流率计算公式的校正系数，饱和流率参数与实时机动车交通量和非机动车(行人)交通量有关。为了能合理确定饱和流率，有效优化配时方案，本文以控制时段重型车辆区间、机动车左转弯车辆区间及非机动车(行人)流量区间计算相关校正系数的区间取值，进而探讨饱和流率区间，即s(I)。

1.2 配时参数区间优化模型构建

以控制时段各进口道机动车交通流率区间为控制输入，选取机动车平均控制延误作为成本型指标，交叉口通行能力作为效益型指标，优化信号配时参数周期时长与各相位绿灯时长，提高交叉口运行效率。信号配时多目标优化模型为

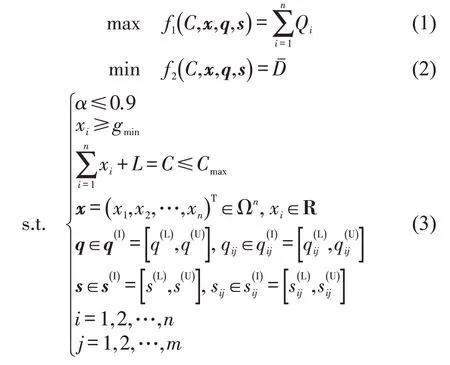
式中：上标(I)、(L)、(U)分别为区间、区间下界、区间上界；fk为不确定目标函数，用区间向量描述，k为目标函数个数，k=1,2；Qi为第i相位机动车通行能力(veh·h-1)，用区间数描述，，Qi公式为

式中：m为第i相位进口道数；θi为第i相位绿信比，；C为周期时长(s)，C≤Cmax；Cmax为最大周期时长(s)；L为损失时长(s)；xi为第i相位绿灯时长(s)；x为n维设计向量，其取值范围为n维向量空间，记为Ωn；n为交叉口相位数；gmin为每相位最小绿灯时长(s)；R 为实数集；sij为第i相位第j进口道机动车饱和流率(veh·h-1)，用区间数描述；为交叉口机动车平均延误，，其

中，为第i相位机动车平均延误(s·veh-1)，用区间数描述，公式为

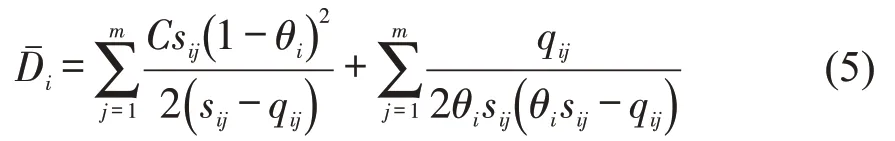
式中：qi为第i相位机动车交通流率(veh·h-1)，为第i相位第j进口道机动车交通流率(veh·h-1)，用区间数描述；q,s分别为n+m维不确定向量，用区间向量q(I),s(I)描述，；α为交叉口饱和度，用区间数α(I)描述，，其计算过程为

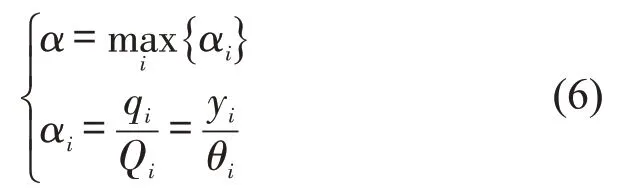
式中：αi为第i相位饱和度，用区间数描述；yi为第i相位交通流量比，为第i相位第j进口道交通流量比，yi，yij为一维不确定向量，分别用区间数，来描述，

1.3 模型修正

依据信号配时原则，交通平峰期要求尽可能减少车辆在交叉口的延误，而在交通高峰期则着重提高交叉口的通行能力，尽可能地提高交叉口通过率，使道路使用率达到最大(逼近饱和流率)。因此，结合多目标规划模型理论及其优选法和交通控制原理，对模型的目标函数式(1)与式(2)进行修正，选取交叉口各相位饱和流率和通行能力差值最小为主要优化目标，以车均延误满足管理者预期要求为约束条件，在保证通行能力达到最优的同时，确保机动车平均延误满足预期要求，模型修正为

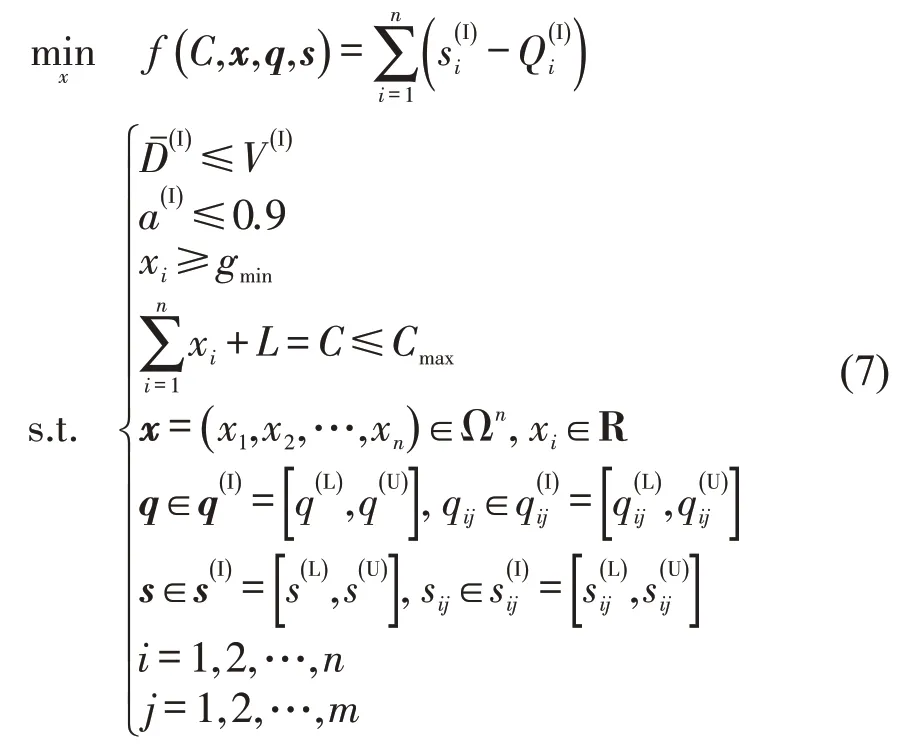
式中：si为第i相位机动车饱和流率区间(v eh·h-1)，用区间数s(iI)描述，为性能区间，即车均延误预期要求，可依据管理者需求进行设置，此处，借鉴交叉口服务水平等级划分标准，选取一级～三级对应的车均延误取值区间，即V(I)=[0,60]，且与饱和度小于0.9 的条件对应。通过分析，式(7)为区间值非线性规划模型，其中，包含两个不确定参数交通流量q与饱和流率s，目标函数与约束条件均含有区间数，且目标函数具有非负性。

根据交叉口交通流需求特性和模型性质，当交叉口为非饱和状态时，通行能力随着绿灯时长的增加而增加，但当绿灯时长达到某一阈值时，通行能力减少，此时，配时方案达到最优，该阈值即为最优绿灯时长。

2 模型转换及算法

2.1 模型转换

2.1.1 区间可能度及约束条件转换模型

信号配时优化模型式(7)中车均延误和饱和度约束条件为区间不确定约束，此处，采用随机机会约束规划中随机约束转换思路对其进行转换，即通过使不确定约束条件的概率满足某一置信水平λ[8]。对于车均延误不大于性能区间V(I)的约束条件，使其可能度不小于可能度水平参数λ1，转换公式为

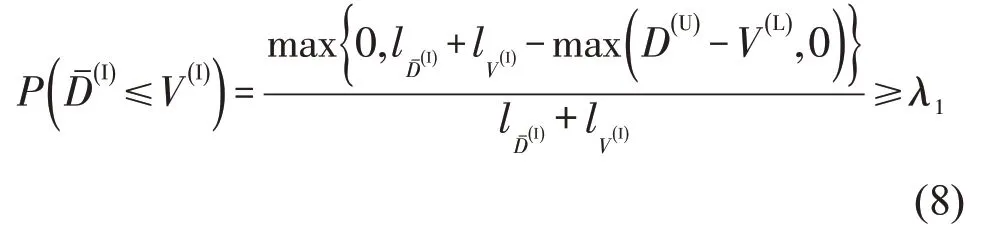
同理，对于饱和度α(I)不大于0.9 的约束条件，使其可能度不小于可能度水平参数λ2。饱和度约束条件等价转换形式为

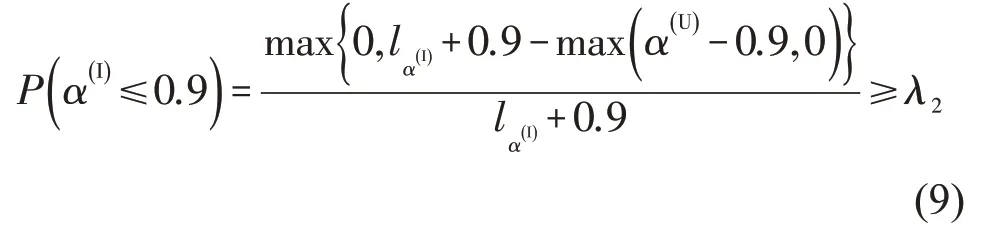
式中：当α(U)≤0.9 时，P(α(I)≤0.9)=1，饱和度α(I)绝对不大于0.9；λ2为饱和度小于0.9 的可能度水平参数，0≤λ2≤1，一般为0.8。

2.1.2 区间序关系及不确定目标函数的转换

当饱和流率为区间数时，信号配时优化模型式(7)为区间值非线性规划模型，其目标函数的可能取值为一区间而非确定的实数值。区间序关系常用于定性判断某区间是否优于或劣于另一区间[8]，因此，本文利用区间序关系处理不确定目标函数。区间序关系的表示形式有很多，考虑到工程问题计算的直观性，此处选择基于区间中点和半径偏好的区间序关系≤cw将不确定目标函数转换成确定性目标函数。具体地，对于最小化优化问题，序关系等价关系[8]为

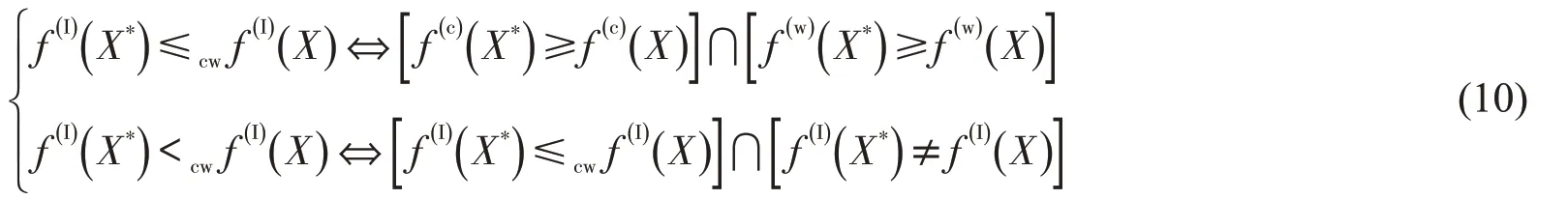
式中：X*为最小化优化问题的最优解；f(I)(X)为区间值目标函数；f(c)(X)为f(I)(X)的中点值；f(w)(X)为f(I)(X)的半径，具体计算公式为

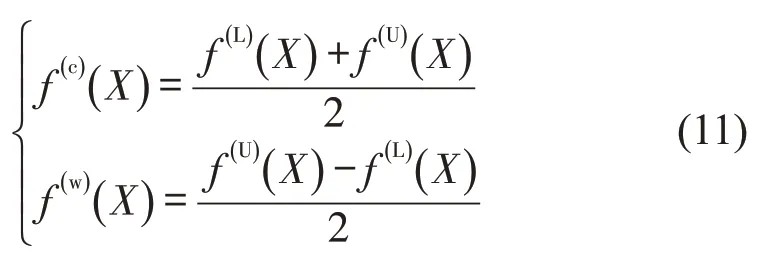
式中：f(L)(X)，f(U)(X)分别为区间值函数f(I)(X)的上、下界，可通过两次优化过程求解不确定目标函数f(I)(X)获得，即

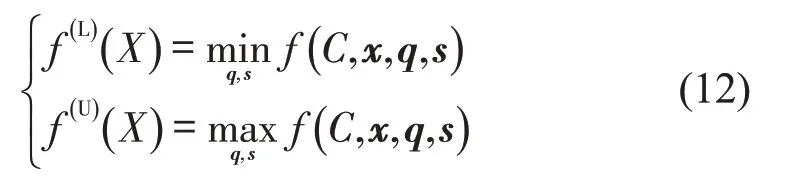
利用区间序关系≤cw，结合式(10)～式(12)，将模型式(7)的区间值目标函数转化为使中点最小和半径最小的多目标函数，具体转换模型为

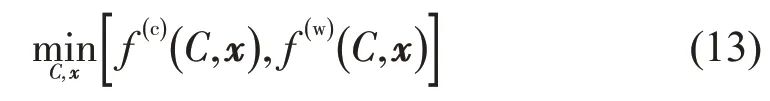
当饱和流率波动较小时，其变化区间可近似为实数，模型式(7)的目标函数为实数，无需进行目标函数转换。

2.1.3 确定性转换模型

当饱和流率为区间数时，综合目标函数与约束条件的转换模型式(13)、式(8)、式(9)，信号配时区间优化模型式(7)转换成等价的确定型多目标优化模型，即

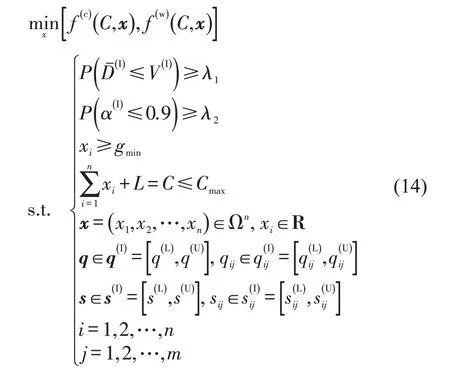
为了便于求解，利用多目标优化中的线性加权法将多目标优化模型式(14)转换成单目标优化模型，即

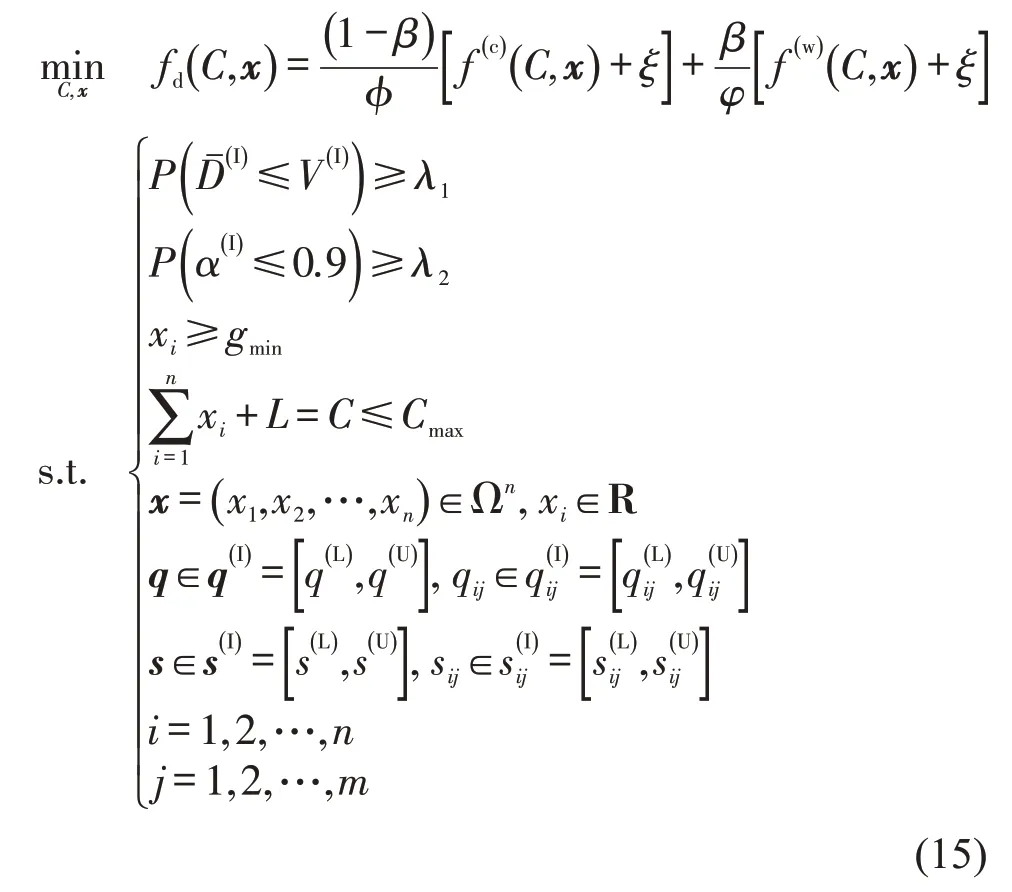
式中：fd为多目标评价函数；0≤β≤1 为权系数；ξ为确保目标函数非负的参数，考虑到实际工程问题，一般取ξ=0；φ,φ为多目标函数的正则化因子，理论上通过优化过程获得，即

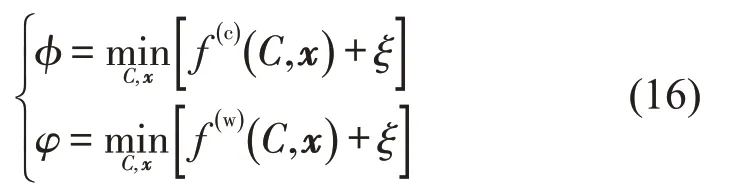
2.2 求解算法

考虑到模型式(15)为多层递阶优化模型，本文采用遗传算法进行求解。为了简化计算，便于参数选取，在求解过程中先对模型式(7)中的目标函数进行量纲处理，即多目标正则化因子φ,φ可以根据具体问题大致取与各自目标同一量级的值，经多次测算，φ=1.3，φ=0.5，控制性能指标的权重参数β=0.5。

算法的具体迭代过程如下：

Step 1 初始化种群。确定染色体编码方案，采用实数向量编码，构造初始化种群。

Step 2 计算适应度函数。针对每个种群个体，计算目标函数与约束条件的区间上、下界，构造适应度函数。

Step 2.1 赋初值。给定初始设计向量X(1)，X(1)为转换后确定型模型式(15)的可行解，满足，且X(1)≥gmin。

Step 2.2 计算多目标评价函数与约束条件。依据式(12)计算目标函数相对于流量区间在X(1)处的区间值并依据式(11)计算不确定目标函数的中点值f(c)(C,X(1))与半径f(w)(C,X(1))，进而计算多目标评价函数fd(X(1))(或f(X(1)))；计算原不确定约束条件在X(1)处的区间与，并依此计算约束的可能度与

Step 3 父体选择。采用轮盘赌选择方法，使得适应度函数值小的个体被优先选择进入下一代，继续进行计算。

Step 4 设置相关参数。选取控制参数，经过对不同参数进行试算，确定算法的种群规模N=20，交叉概率pc=0.5 和变异概率pm=0.05。其中，交叉算子采用常规算子，变异算子则采用非一致性变异，使得在搜索末期能以一定的概率跳出当前搜索区，防止陷入局部最优。

Step 5 终止准则判断。确定算法的终止准则，本文选取迭代次数达到500代或目标函数差值10-6为算法终止条件。若进化代数满足上述终止条件，则输出最优解；否则，对父代种群实施选择、交叉及变异操作，形成子代种群个体，然后，依据个体适应度形成下一代种群，并返回Step 2。

3 模型验证及适应性分析

3.1 模型验证

3.1.1 数据准备

为了验证信号配时区间优化模型的可行性，首先，选取道路等级相差较大，各进口道重型车辆占比较大，非机动车左转占比较大，且无左转专用相位的两相位信号交叉路口进行数据采集，其中，东、西相位各进口道数为4，南、北相位各进口道为单车道，车道宽度均为3.5 m，具体几何构型如图1所示，未对非机动车道进行详细描述。

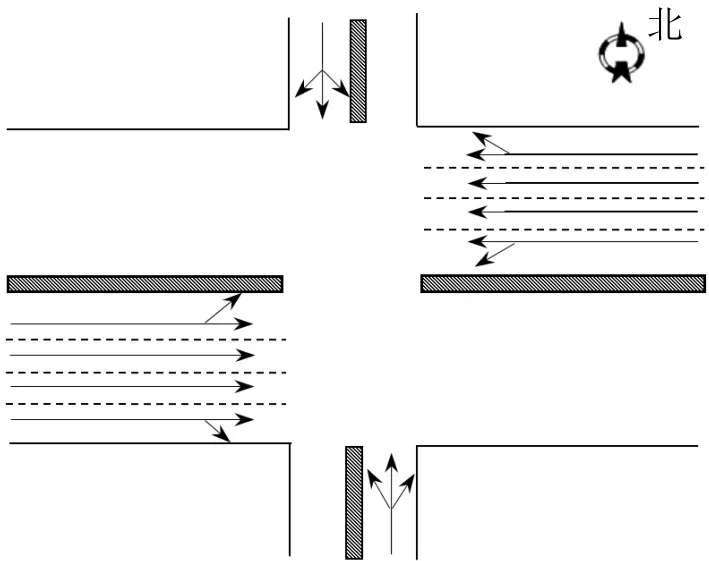
图1 交叉口1的几何构型Fig.1 Plan of intersection 1

交叉口各进口道5 min 采集标段交通量数据，考虑到实际情况与模型需求，仅给出各进口道机动车直左5 min交通量，非机动车左、右转、直行5 min交通量。因为，行人交通无左转，本文中主要为非机动车左转交通量。交通量统计如表1所示。

3.1.2 模型计算

由表1计算出饱和流率相关校正系数，其余系数为1。其中，机动车左、右转校正系数适用于共用车道，左、右转专用道上的左、右转校正系数取值为0.95。各进口道饱和流率相关校正系数如表2所示。

依据表1和表2，各进口道饱和流率区间与交通量区间如表3所示。其中，东西相位为关键相位，饱和流率区间距离较大，说明高峰期东西进口道受车道间左、右转车辆以及非机动车等因素的干扰较大。

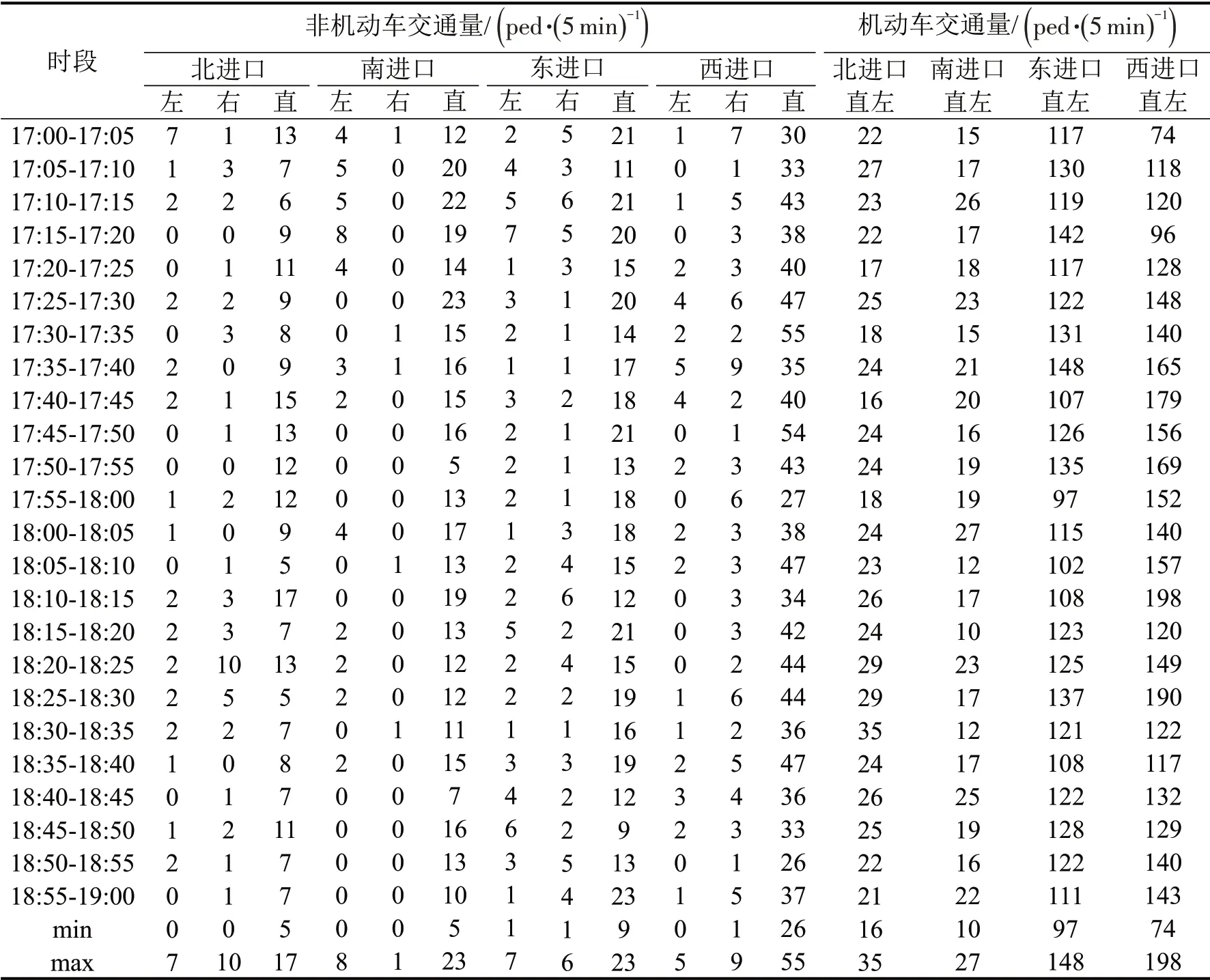
表1 交叉口1的5 min时段交通量Table 1 Traffic flow at intersection 1 within 5 minutes

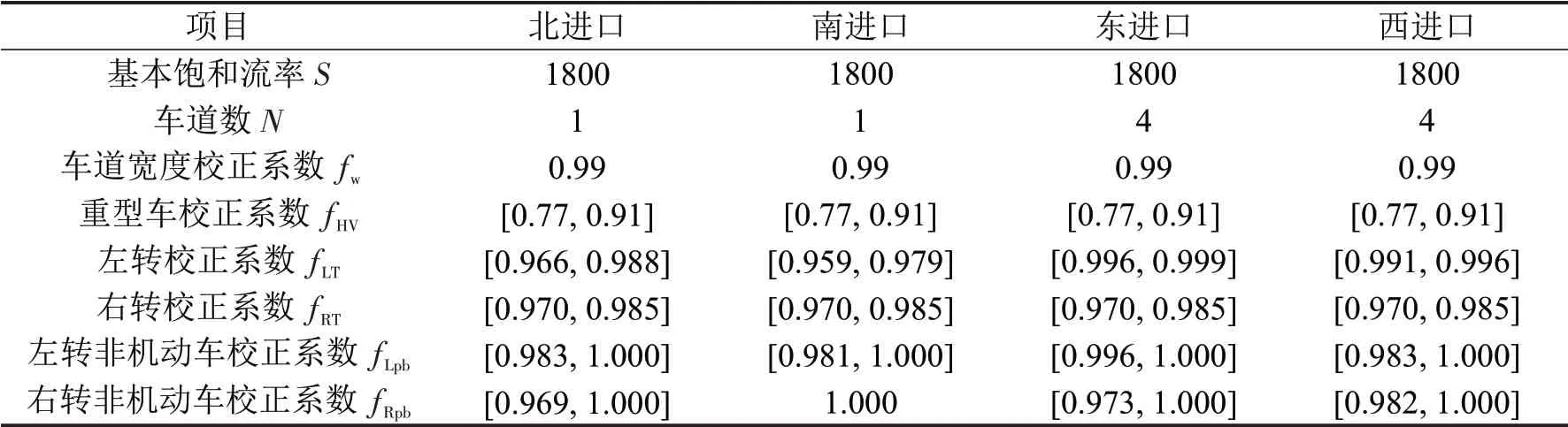
表2 交叉口1各进口道饱和流率相关校正系数Table 2 Correction coefficient of saturated flow rate of entrance road at intersection 1

表3 交叉口1交通量区间和饱和流率区间Table 3 Calculation results of traffic flow interval and saturated flow rate interval at intersection 1

经过多次测算，相关参数设置如下：β=0.5，ξ=0，φ=1.3，φ=0.5，ε=10-6，初始设计向量x(1)=[1 5,15]T。经计算，得到各信号配时方案，其中，全红时长为2 s，黄闪时长为3 s。方案1为考虑饱和流率区间的配时参数多目标区间优化模型；方案2 表示饱和流率为均值的配时参数多目标区间优化模型；方案3为以车均延误与通行能力为控制性能指标的多目标信号配时；鲁棒优化采用盒式不确定集，即晚高峰期17:00-19:00 的交通量，间隔为10 min，选取每间隔机动车延误与标准差最小作为鲁棒优化目标函数[7]。

在表4中，方案1和方案2可行，且车均延误区间介于[0,60]满足预期要求。计算结果表明，6 种方案均可行，且方案1 和方案2 适用于表3所示的交通量区间。

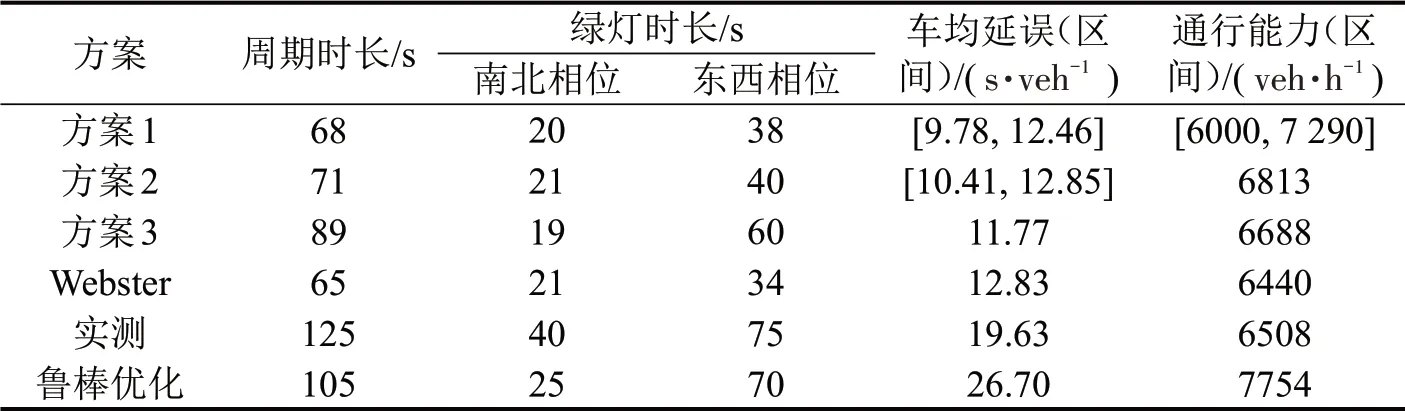
表4 交叉口1各种配时方案计算结果Table 4 Calculation results of signal timing parameters in intersection 1

3.1.3 仿真比较

为了分析信号配时区间优化方法的有效性，进一步利用VISSIM 软件对各方案进行仿真比较，结果如图2和图3所示。图2为交叉口1 各方案的车均延误对比图，方案1优于其他方案；图3为各方案通行能力对比图，方案1 优于其他方案，较Webster方法的优化程度如表5所示。

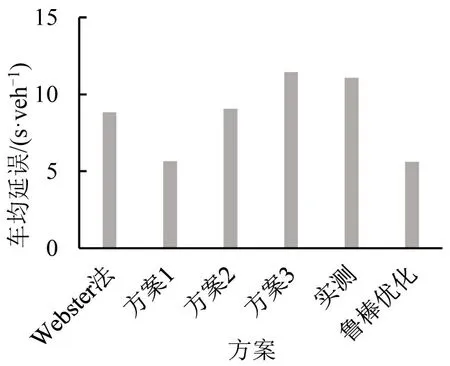
图2 交叉口1各方案平均延误对比Fig.2 Comparison of average delays for all methods at intersection 1

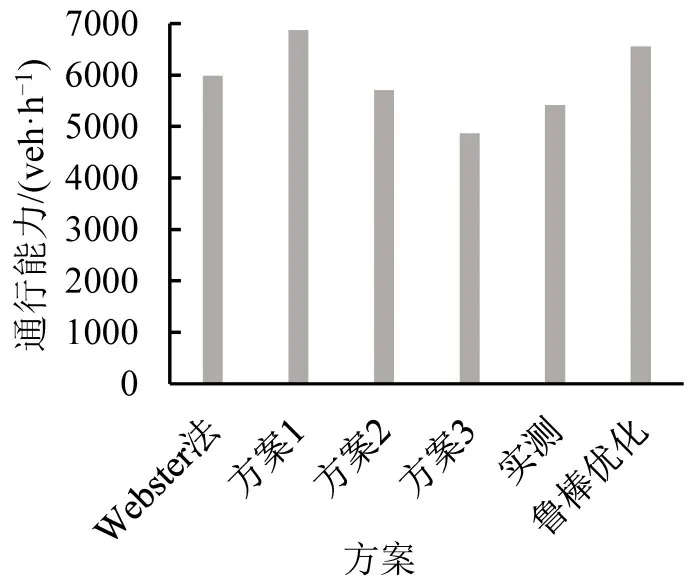
图3 交叉口1各方案通行能力对比Fig.3 Comparison of capacities for all methods at intersection 1

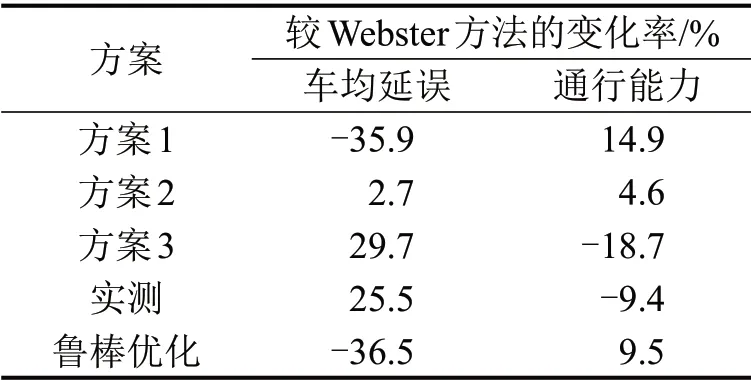
表5 交叉口1控制指标优化程度Table 5 Degrees of optimization for all control indexes at intersection 1

结果表明：方案1平均延误减少了35.9%，通行能力提高了14.9%，表现出较强的有效性；方案2，车均延误增加了2.7%，通行能力降低了4.6%；方案3车均延误增加了29.7%，通行能力降低了18.7%；鲁棒优化车均延误减少了36.5%，通行能力提高了9.5%。说明，信号配时区间优化模型是有效的，当考虑饱和流率区间时，表现出更优的控制效果(方案1较鲁棒优化在通行能力上略提高了4.9%)。

3.2 模型适应性分析

为验证模型的适应性，选取存在左转专用相位的三相位信号交叉路口进行交通数据采集，其几何构型如图4所示，其中，南北进口道为5 车道，西进口道为4 车道，东进口为单车道，车道宽度为3.5 m。

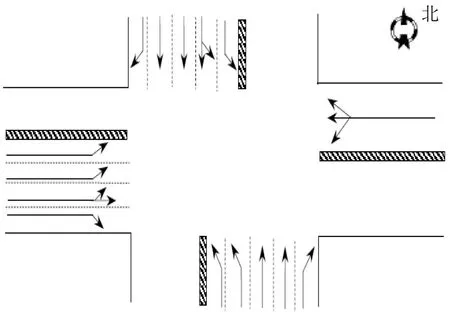
图4 交叉口2的几何构型Fig.4 Plan of intersection 2

通过计算，各进口道交通量区间和饱和流率区间如表6所示，其中，西进口道饱和流率区间相对波动较大。

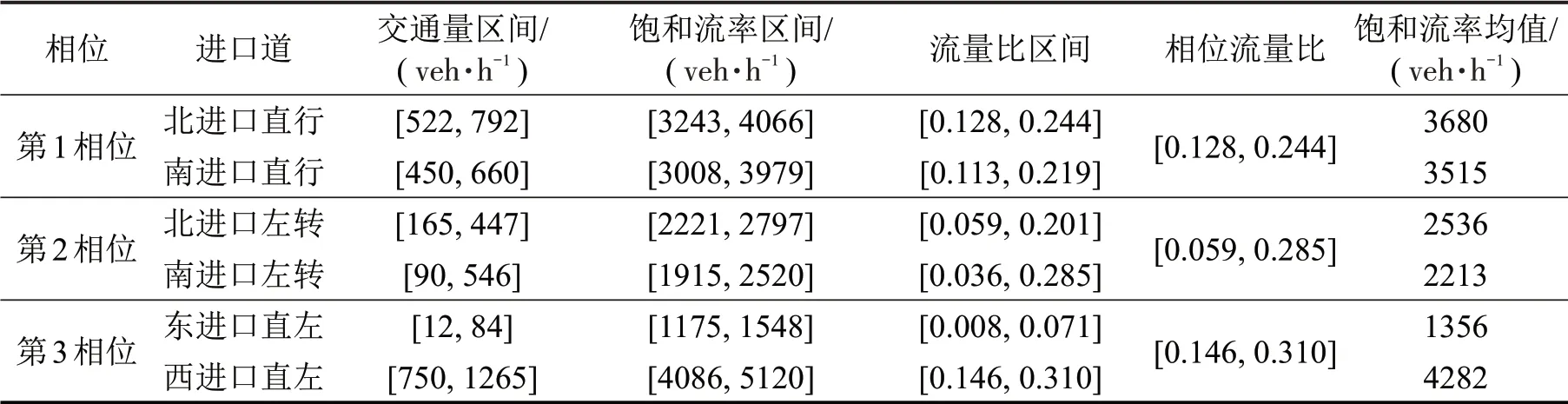
表6 交叉口2交通量区间和饱和流率区间Table 6 Calculation results of traffic flow interval and saturated flow rate interval at intersection 2

为了能获得更优的目标函数性能，经多次测算，约束条件可能度参数取值为0.7，扩大模型式(15)的可行域，计算结果如表7所示，其中，车均延误区间上界略大于60 veh·h-1，约束可能度为0.72。

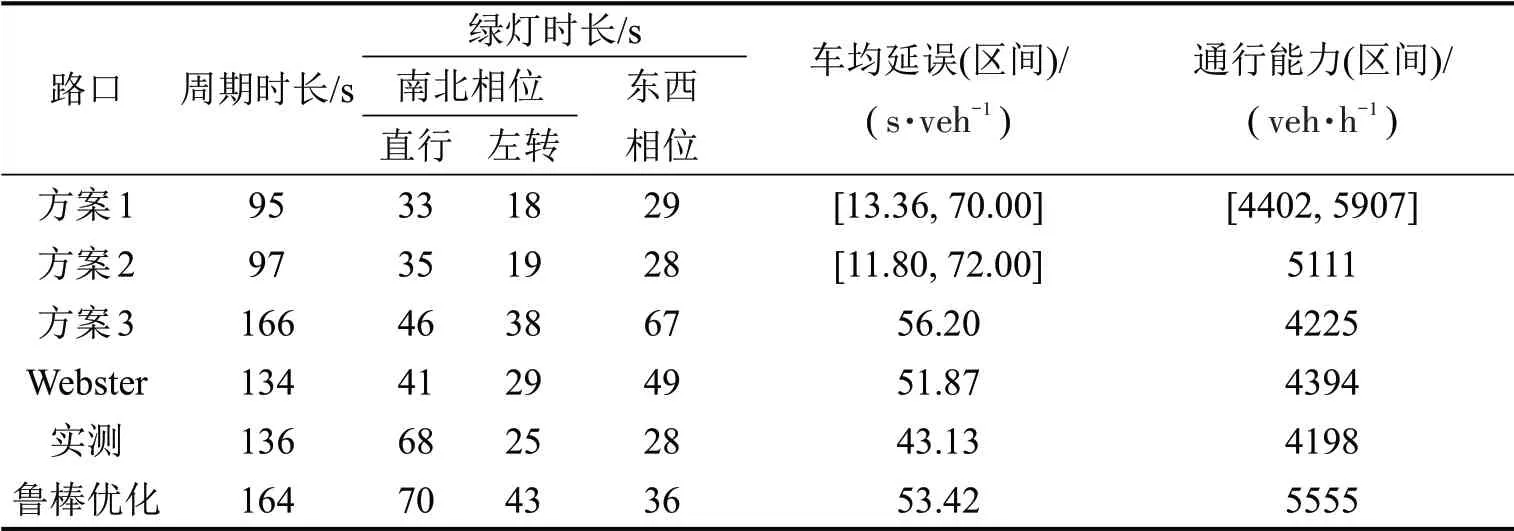
表7 交叉口2各种配时方案计算结果Table 7 Calculation reslts of signal timing parameters in intersection 2

进一步，利用VISSIM 软件对交叉口2 各配时方案进行仿真比较，结果如图5和图6所示。图5为机动车平均延误对比图，方案2 优于其他方案；图6为通行能力对比图，方案2 优于其他方案。通过与Webster方法比较，优化程度如表8所示。

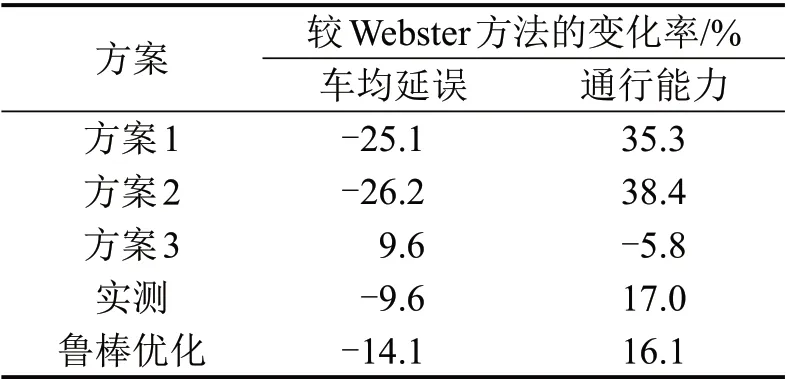
表8 交叉口2各控制指标优化程度Table 8 Degrees of optimization for all control indexes at intersection 2

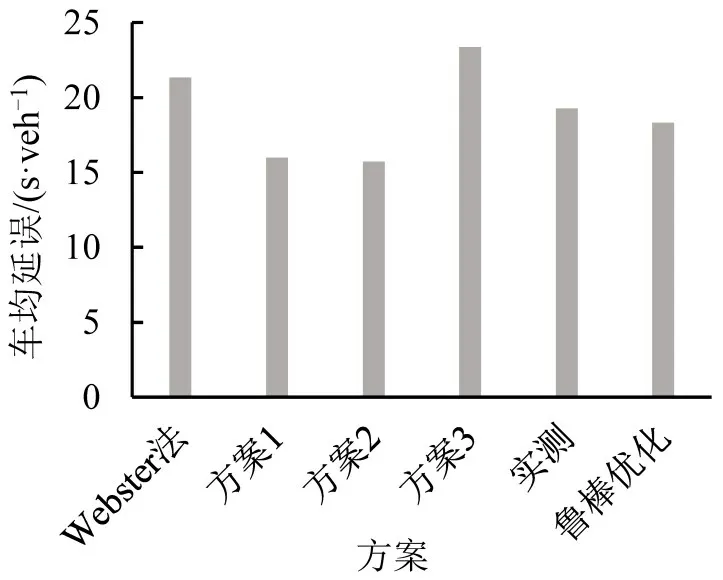
图5 交叉口2各方案平均延误对比Fig.5 Comparison of average delays for all methods in intersection 2

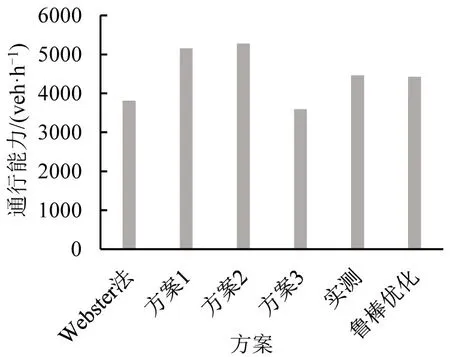
图6 交叉口2各方案通行能力对比Fig.6 Comparison of capacities for all methods in intersection 2

结果表明：方案2平均延误减少了26.2%，通行能力提高了38.4%，表现出较强的有效性；方案1车均延误减少了25.1%，通行能力提高了35.3%；鲁棒优化车均延误减少了14.1%，通行能力提高了16.1%；方案3车均延误增加了9.6%，通行能力降低了5.8%。显然，方案1 与方案2 优化程度相当，方案2略优于方案1。

4 结论

本文以交通量区间作为信号控制输入参数，通过分析饱和流率的不确定性，构建信号配时参数多目标区间优化模型，并与多目标信号配时、Webster方法、鲁棒优化方法及实测方案进行比较。结果表明：

(1)信号配时多目标区间优化方法是可行有效的；

(2)带饱和流率区间的优化方法对于饱和流率波动较大的无左转专用相位的两相位交叉口，较传统Webster 方法平均延误减少了35.9%，通行能力提高了14.9%，略优于鲁棒优化(通行能力略提高4.9%)，控制效果较优；

(3)饱和流率为实数的区间优化方法适用于带左转专用相位的三相位交叉口，较Webster 方法平均延误减少了26.2%，通行能力提高了38.4%，且优于鲁棒优化(车均延误减少了14.2%，通行能力提高了19.3%)；

(4)用区间数描述不确定参数交通量和饱和流率，一方面，界定控制方案的适用范围，提高控制方案的适用性；另一方面，用区间数进行参数估计，优化信号配时，在一定程度上降低交通流实时检测与预测的难度，减少参数估计误差，为不确定环境下交通控制系统的研究提供理论基础，但在模型求解过程中，进行参数选取时会受到设计者主观偏好的干扰，从而影响控制方案的设计性能。为此，将进一步深入探讨区间非线性规划模型及其求解算法，使其更广泛地适用于城市交通信号控制。此外，本文仅以单交叉口定时控制为背景，对配时参数区间优化模型进行验证，并未考虑实时控制方案配时参数区间优化模型。为此，将进一步从区间预测的角度，深入探讨实时控制信号配时参数区间优化模型。