山区双车道公路货车碰撞预测的双变量冲突极值模型

戢晓峰，耿昭师

(昆明理工大学，交通工程学院，昆明 650500)

0 引言

山区双车道公路弯急坡陡、道路狭窄且货车比例高，货车行驶过程中易发生超速、超载等高风险驾驶行为，导致交通事故频发[1]。据统计，山区双车道公路的交通事故发生率占全部公路的15%以上[2]，而山区双车道公路上涉及货车的交通流碰撞率较高[3]。显然，山区双车道公路货车事故治理已经成为交通安全研究者及管理者关注的重大现实问题。

目前，货车与其他车辆的交互作用机制逐步受到国内外学者关注，主要集中于历史事故数据的宏观分析。由于货车事故数据难以采集，利用交通冲突指标探索单个货车冲突越来越受学者欢迎。如Kyung 等[4]利用车头时距，发现货车和各类车辆的交互作用与碰撞可能性显著相关；Dhwani等[5]使用避撞减速度发现，货车阻碍了非货车驾驶员的视线并延迟了他们的规避行动。但是，现有研究多基于城市道路或高速公路，对山区双车道公路货车安全的研究较为鲜见，而Khorashadi 等[6]分析了加利福尼亚州4年的事故数据，发现城市道路和农村道路上货车事故存在显著差异。

近年来，极值理论(Extreme Value Theory,EVT)在交通安全领域得到广泛应用。最初，EVT通过单变量模型建立单一交通冲突指标与碰撞之间关系，Campbell 等[7]提出了用于交通冲突的EVT，之后Songchitruks 等[8]基于EVT 建立了交通冲突和碰撞关系的外推方法，使得EVT 在交通安全预测方面越来越流行，郑来等[9]利用单变量冲突极值模型(Univariate Traffic Conflict Extreme Value,UTCEV)

预测扩建后交叉口左转弯碰撞事故减少了63.9%。但学者发现单一冲突指标仅能代表冲突事件的部分严重性，因此，整合不同指标的适用性有助于更全面地评估交通安全。Jonasson等[10]引入双变量极大值模型将TTC和一个解释变量组合，研究自然驾驶的追尾碰撞。随后，Zheng 等[11]利用双变量极值理论建立了广义极值分布和广义帕累托分布的单双变量极值模型，发现双变量广义帕累托分布模型预测性能最佳。Cavadas等[12]开发了非平稳双变量极值模型来估计农村双车道公路超车过程的正面和追尾碰撞的联合概率。总体而言，双变量冲突极值模型(Bivariate Traffic Conflict Extreme Value,BTCEV)比UTCEV 模型预测性能好，但BTCEV模型主要用于交叉口及高速公路的交通事故预测，较少用于山区双车道公路，在货车碰撞预测方面更是接近空白。

综上，鉴于山区双车道公路货车碰撞的频发性和严重性，单一冲突指标无法全面进行货车碰撞分析。因此，针对山区双车道公路货车碰撞预测的现实需求及研究不足，本文利用视频轨迹数据，观察山区双车道公路货车与交互车辆的不同运行轨迹，选取碰撞时间(Time to Collision，TTC)和后侵入时间(Post Encroachment Time，PET)，构建山区双车道公路货车碰撞预测的BTCEV模型。

1 冲突指标选取及计算

1.1 冲突指标选取

交通冲突是指两个或多个道路参与者在空间和时间无限接近，如果不采取避险措施就会发生碰撞。在已开发出的各种冲突指标中，TTC和PET使用最广泛[13]。但是，TTC 和PET 仍存在局限性：TTC适用于轨迹相同的冲突，不能完全捕捉相交轨迹的冲突情况；PET 一般只能用于轨迹相交的冲突，因为跟驰状态下，若后车速度低于前车，也会产生一个PET 值，但这种情况不会发生碰撞。而将TTC 和PET 组合起来能避免使用单一指标带来的碰撞预测误差，Zheng 等[14]对4 个交通冲突指标进行6种组合，发现TTC和PET组合对碰撞发生的预测最准确。因此，本文选用TTC和PET进行山区双车道公路货车碰撞预测，研究流程如图1所示。

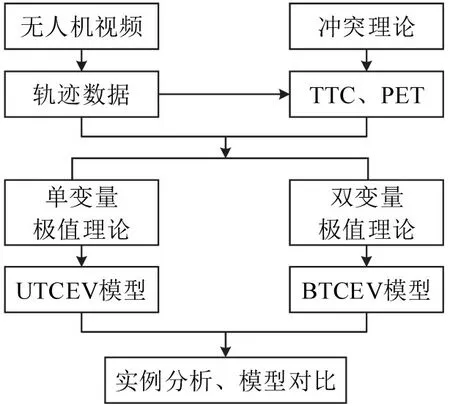
图1 研究流程图Fig.1 Research flow chart

1.2 冲突指标计算

(1)TTC计算

TTC指若后车速度大于前车时，两车以原来的速度和轨迹行驶，则将发生碰撞，那么从冲突开始到碰撞发生的时间就是碰撞时间。TTC计算公式为

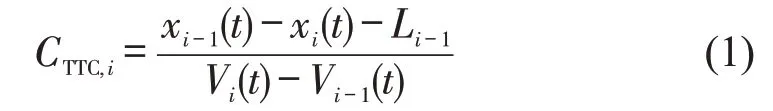
式中：CTTC,i为i-1 车(前车)与i车(后车)的碰撞时间；xi-1(t)、xi(t)分别为t时刻前车和后车的位置；Li-1为前车车长；Vi-1(t)、Vi(t)分别为t时刻前、后车的瞬时速度。

(2)PET计算

PET 指前车车尾通过冲突线的时间与后车车头到达冲突线的时间之差。PET计算公式为

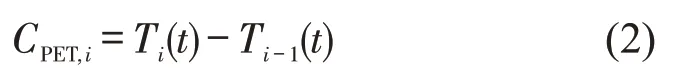
式中：CPET,i为i车(后车)与i-1 车(前车)的后侵入时间；Ti-1(t)为t时刻前车车尾离开冲突线的时间；Ti(t)为t时刻后车车头到达冲突线的时间。

2 货车碰撞预测的冲突极值模型

EVT 主要用于分析随机过程中极小概率事件的发生概率和统计分布，分为区组最大值模型(Block Maxima,BM)和超阈值(Peaks-overthreshold,POT)模型，相比于BM 模型，POT 模型能够充分利用极值信息，且样本数量较小时表现良好[15]，故利用POT模型进行山区双车道公路货车碰撞预测。基于交通冲突建立POT 模型的基本思想为：当TTC(PET)小于等于0 s意味着冲突指标达到极端水平，交通冲突就会产生碰撞，而POT 模型关注于大于阈值的极值分布，因此对TTC和PET取负映射，其值越大表示冲突越严重，即当-TTC(-PET)大于等于0 s表示发生碰撞。

2.1 UTCEV模型

设X1,X2,…,Xn是具有相同分布函数的独立随机变量，对于足够大的阈值u，若超阈值Xi＞u，则超出量Y=Xi-u服从广义帕累托分布(Generalized Pareto Distribution,GP)，分布函数为

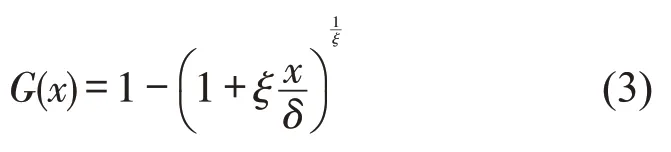
式中：G(x)为GP 分布表达式；δ为尺度参数；ξ为形状参数；x为超阈值极值。

由于引发碰撞的冲突仅为交通冲突的很小部分，故应更加关注交通冲突的尾部分布。尾部分布近似为GP分布，即

式中：为尾部的GP 分布；Nu为X1,X2,…,Xn中超过u的个数。

2.2 BTCEV模型

通过观察发现，山区双车道公路上货车与交互车辆很少出现运行轨迹完全相同或交叉角度很大的情况，如果以单一的TTC或PET预测山区双车道公路货车碰撞，可能存在较大的偏差。因此，将TTC 和PET 组合起来是非常有必要的。双变量极值理论对两个极值变量的联合分布进行建模，能够将TTC和PET纳入统一的道路安全评价框架。

设 (Xm,Ym)，m=1,2,…,n是随机向量(X,Y)～F(x,y)的独立同分布样本，对于足够大的ux和uy，F(x,y)的边缘尾部分布近似为式(4)，参数分别为(ζx,δx,ξx)和(ζy,δy,ξy)，其中，ζx=Pr(X＞ux)，ζy=Pr(Y＞uy)。将随机变量X，Y变换为

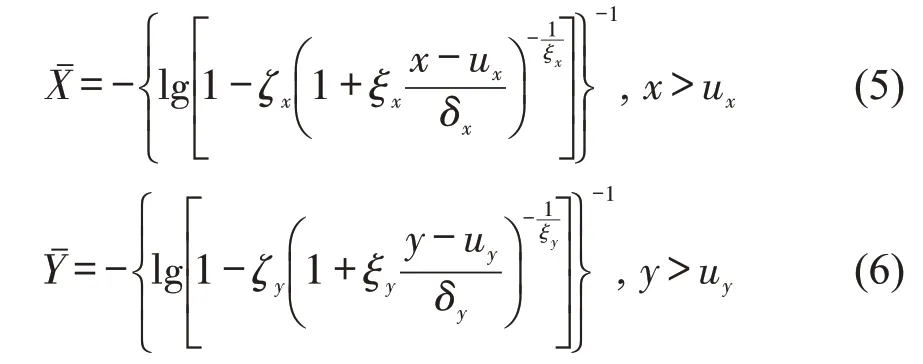
式中：、为X，Y变换参数，且近似为标准Fréchet分布。

因此，F(x,y)的联合分布近似为二元广义帕累托分布，即

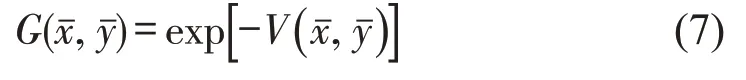
式中：、为、超阈值参数。

对于BTCEV模型的Logistic类型，有

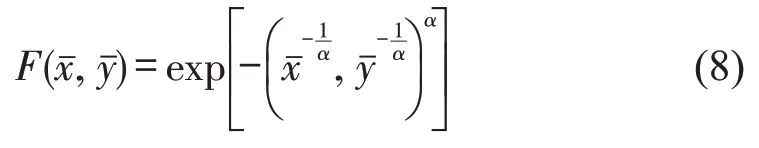
式中：α为拟合Logistic 类型中的未知参数，α∈(0,1)。

2.3 货车碰撞预测

极值理论能够从频繁的交通冲突中预测极少发生的碰撞，碰撞风险概率R为-TTC大于等于0 s或-PET大于等于0 s时货车碰撞发生的概率。

UTCEV模型的尾部估计为

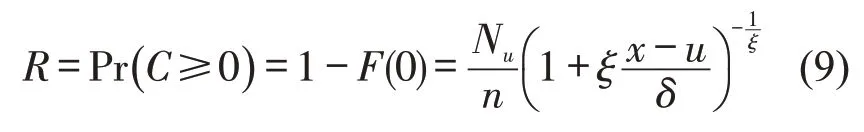
式中：C为-PET或-TTC，若C为-PET，则为C-PET；若C为-TTC，则为C-TTC。

BTCEV模型的尾部估计为

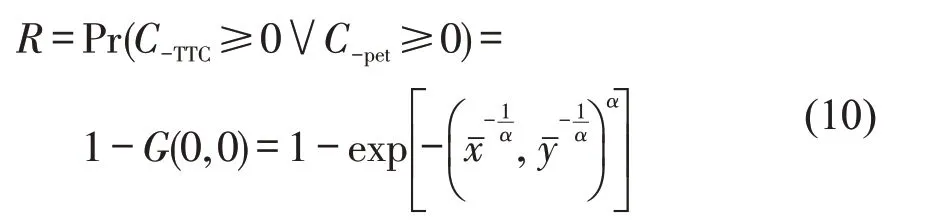
假设观测周期T的样本数据能够反映较长时间(通常为1年)的总体样本特征，那么预测货车碰撞次数为

式中：N为预测的货车年事故发生率。

预测准确性(Prediction Accuracy，Pa)的表达式为

式中：Na为实际的货车年事故发生率。

3 实例分析

3.1 数据采集与提取

(1)数据采集

元(谋)-双(柏)公路是云南省一条典型的山区双车道公路，全长162.0 km，路基宽8.5 m，平曲线最小半径125 m，最大纵坡为7%。为预测山区双车道公路货车发生的碰撞，本文选取元双公路货车混入率较高的3个路段作为研究对象，路段基本信息如表1所示。利用大疆御MAVIC2 无人机，在晴朗天气下进行高空拍摄，拍摄高度控制在200 m 左右，待无人机降落后将数据导入电脑中存储，无人机视频参数及格式如表2所示。

交警现场采集元双公路2013—2017年事故数据4022 条，其中货车事故615 条，占事故总数的15.29%。对货车事故进行统计分析，发现元双公路货车事故造成30 人死亡、380 人受伤，分别占死亡与受伤人数的26.78%和15.56%。鉴于视频数据采集的特殊条件，本文筛选出晴朗天气下8:00-20:00的货车事故数据，共计431 条，货车事故发生率为86.2起⋅年-1。图2为研究路段交通现状及视频截图。

图2 研究路段交通现状及视频截图Fig.2 Research on road traffic status and video screenshots

(2)数据提取

将视频由MP4 格式转为AVI 格式，并导入George2.1 视频处理软件，当货车与交互车辆都完全进入视频画面时添加基准点，获得货车与交互车辆的ID 和图像坐标，通过George2.1 坐标转换功能，将图像坐标与地面坐标进行转换，控制地面点坐标的精度误差在±0.05 m之内，以10 Hz的频率开始提取行驶轨迹数据，直到货车和交互车辆完全驶出视频画面，至此货车和交互车辆分别获得一条完整的行驶轨迹数据，轨迹数据属性包括时间、车辆ID、车辆横向和纵向坐标位置、速度、加速度等，利用货车与交互车辆的ID 及行驶轨迹提取的时间进行匹配，得到一辆货车与其交互车辆的视频轨迹数据。

在轨迹数据中可清晰观察到车辆每帧的运行轨迹、偏移状况及加速度等情况，因此，跟驰冲突中若后车出现持续减速过程，则从后车减速开始时判定交通冲突开始，减速结束表示冲突结束；超车冲突中从后车偏离车道中心线标志着冲突开始，超车车辆完成并道标志着冲突结束。从冲突开始到冲突结束的轨迹称为冲突轨迹。此外，本文为区别于交叉轨迹和相同轨迹，将交叉角度很小，但与相同轨迹极为相似的运行轨迹称为偏移轨迹，偏移轨迹是一种特殊的交叉轨迹，同时具有交叉轨迹和相同轨迹的性质。

将提取出的轨迹数据导入Excel 中，根据式(1)和式(2)同时计算TTC 和PET，而本文根据TTC 的定义，认为后车的速度小于前车速度时，就不发生交通冲突，避免了后车速度低于前车仍会产生一个PET值的问题。

为排除车辆间的正常交互作用，仅考虑TTC小于20 s[16]和PET小于4 s的车辆交互事件，为保证交通冲突的鲁棒性，分别选取冲突轨迹中10 个最小的TTC 和PET，其平均数即为交通冲突值，共提取到120条冲突数据，其中跟驰冲突100条，超车冲突20条。数据提取及处理流程如图3所示，货车与冲突车辆部分冲突数据如表3所示。

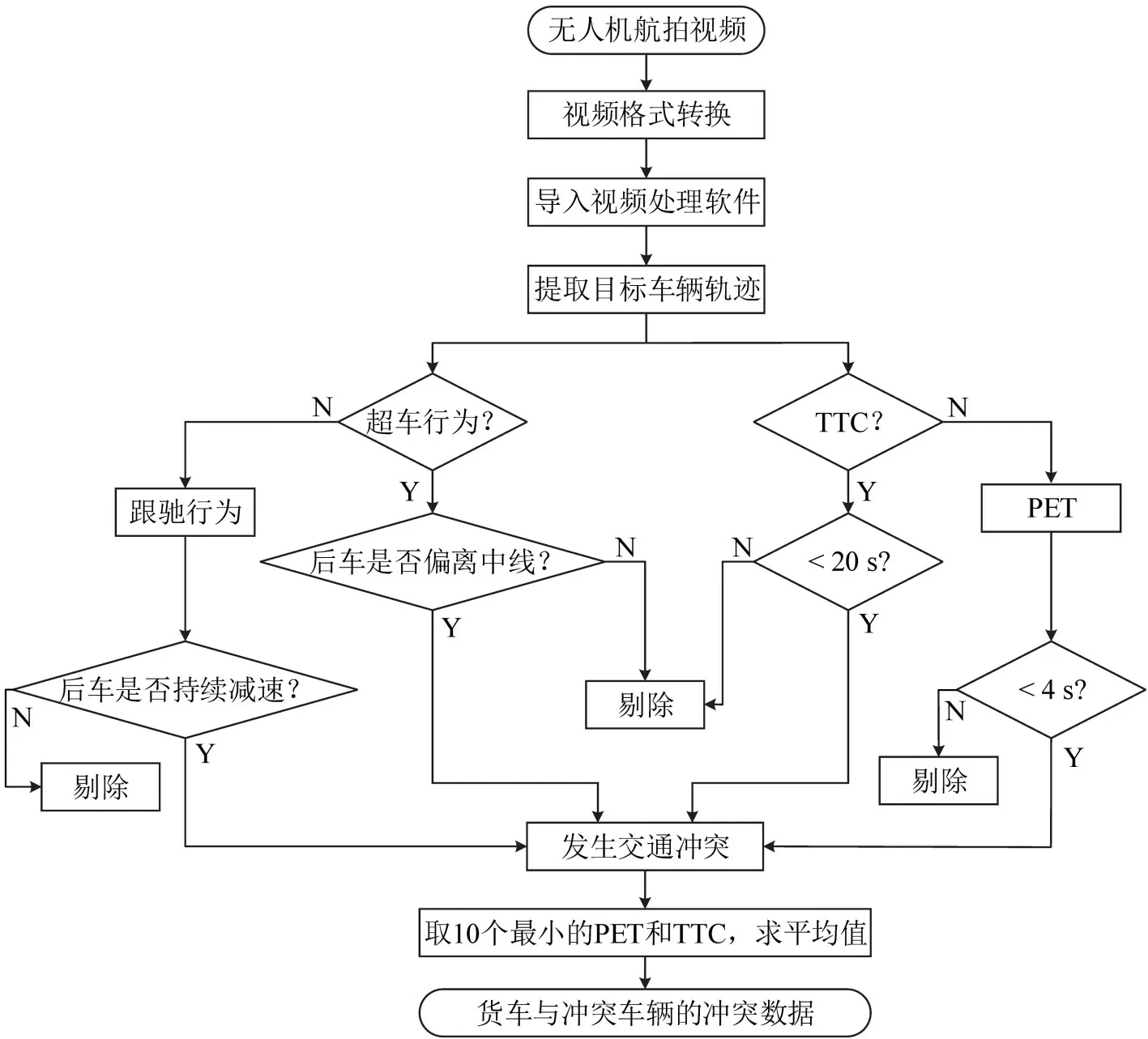
图3 数据采集及处理流程图Fig.3 Data acquisition and processing flow chart

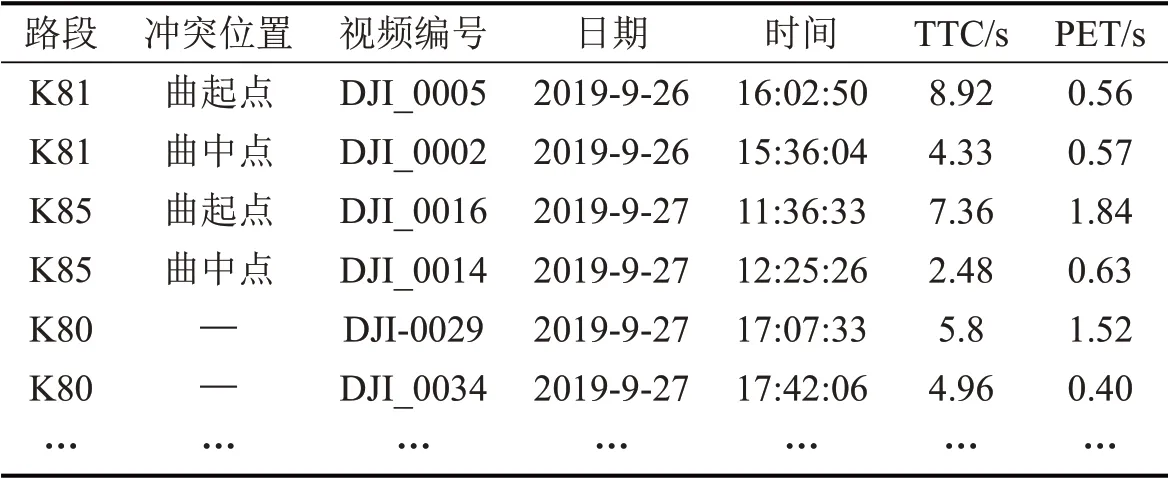
表3 货车与冲突车辆部分冲突数据Table 3 Partial conflict data for trucks and conflict vehicles

3.2 UTCEV模型结果

(1)阈值选择

选择合理的阈值是POT模型的关键，阈值过高会增大参数估计方差，阈值过低会造成有偏估计。本文使用平均剩余寿命图确定阈值的选择范围R1，再利用阈值稳定图确定阈值的稳定范围R2，将两个范围取交集：R=R1∩R2，并以R的上界u+作为最终阈值。

据图4和图5得，-PET 的阈值选择范围Rpet,1=(-0.651,-0.195)，阈值稳定范围Rpet,2=(-0.494,-0.382)，阈值范围为Rpet=Rpet,1∩Rpet,2=(-0.494,-0.382)，最终阈值为-PET等于-0.382 s。

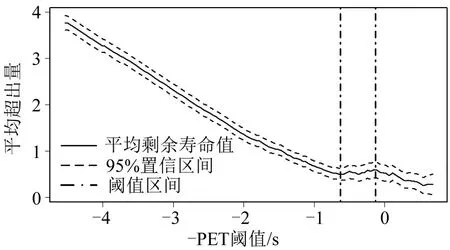
图4 -PET平均剩余寿命图Fig.4 Negative PET average residual life plot

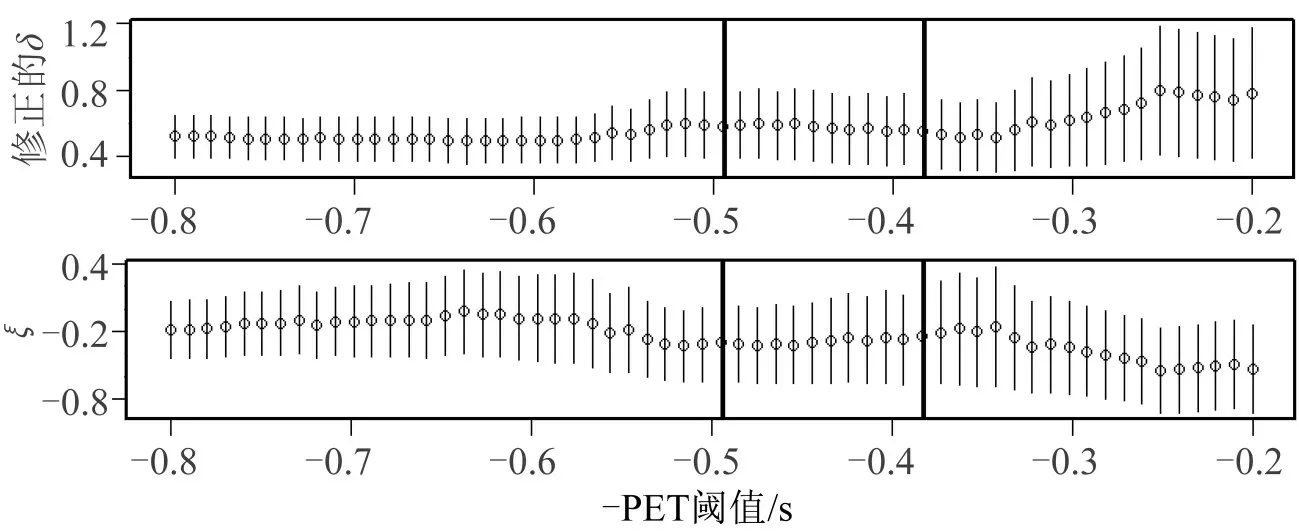
图5 -PET阈值稳定性图Fig.5 Negative PET threshold stability plot

类似的，从图6和图7可得，Rttc,1=(-8.125，-4.471),Rttc,2=(-5.584,-4.392)，Rttc=Rttc,1∩Rttc,2=(-5.584,-4.471)，最终阈值为-TTC等于-4.471 s。

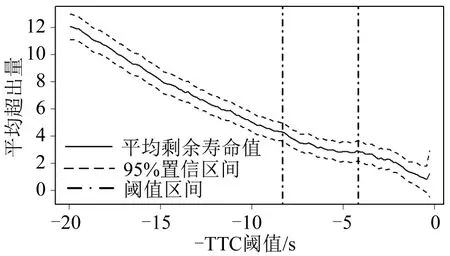
图6 -TTC平均剩余寿命图Fig.6 Negative TTC average residual life plot

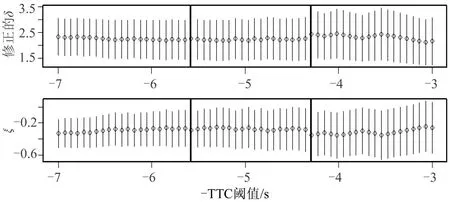
图7 -TTC阈值稳定性图Fig.7 Negative TTC threshold stability plot

(2)模型检验

从图8(a)可以看出，QQ 图中所有的点几乎都分布在拟合直线上，表明PET 模型的拟合效果良好。从图8(b)可知，虽然QQ 图中的部分点偏离拟合直线，但从图8(d)来看，预测的重现水平在95%的置信区间内，表明TTC模型拟合效果仍然较好。

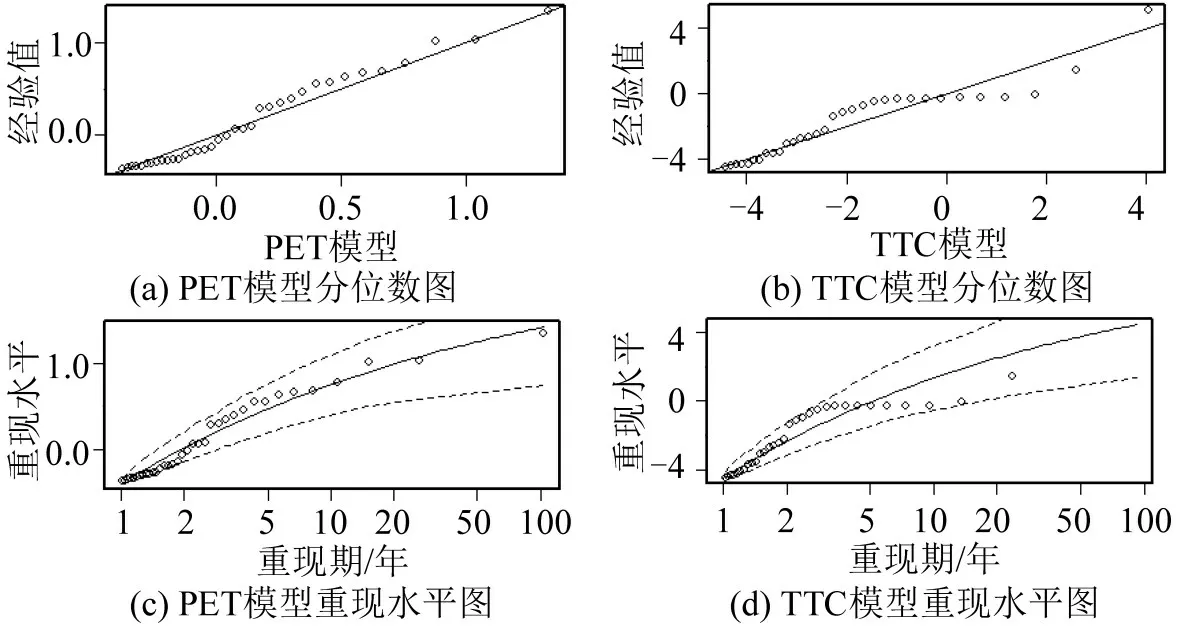
图8 UTCEV模型检验图Fig.8 UTCEV model test plot

(3)货车碰撞预测

使用极大似然函数对UTCEV模型进行参数估计，估计结果如表4所示。

表4 UTCEV模型的参数估计结果Table 4 Parameter estimation results of UTCEV model

根据式(9)可得

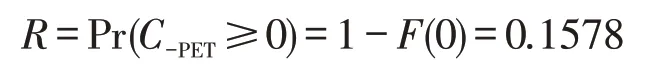
以PET 等于0.382 s 为山区双车道公路货车严重冲突阈值，当PET小于等于0 s时，山区双车道公路货车碰撞发生概率为15.78%，根据式(11)，山区双车道货车事故发生率为230.44起⋅年-1。

同理，可得

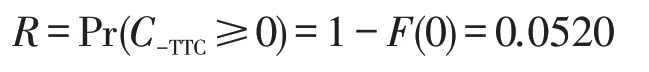
TTC等于4.471 s时，山区双车道公路货车发生严重交通冲突，当TTC小于等于0 s时，山区双车道公路货车发生事故的概率为5.20%，山区双车道货车事故发生率为75.96起⋅年-1。

3.3 BTCEV模型结果

(1)货车碰撞预测

为避免模型中只有一个分量超过阈值，BTCEV 模型使用截尾极大似然函数进行参数估计，估计结果如表5所示。

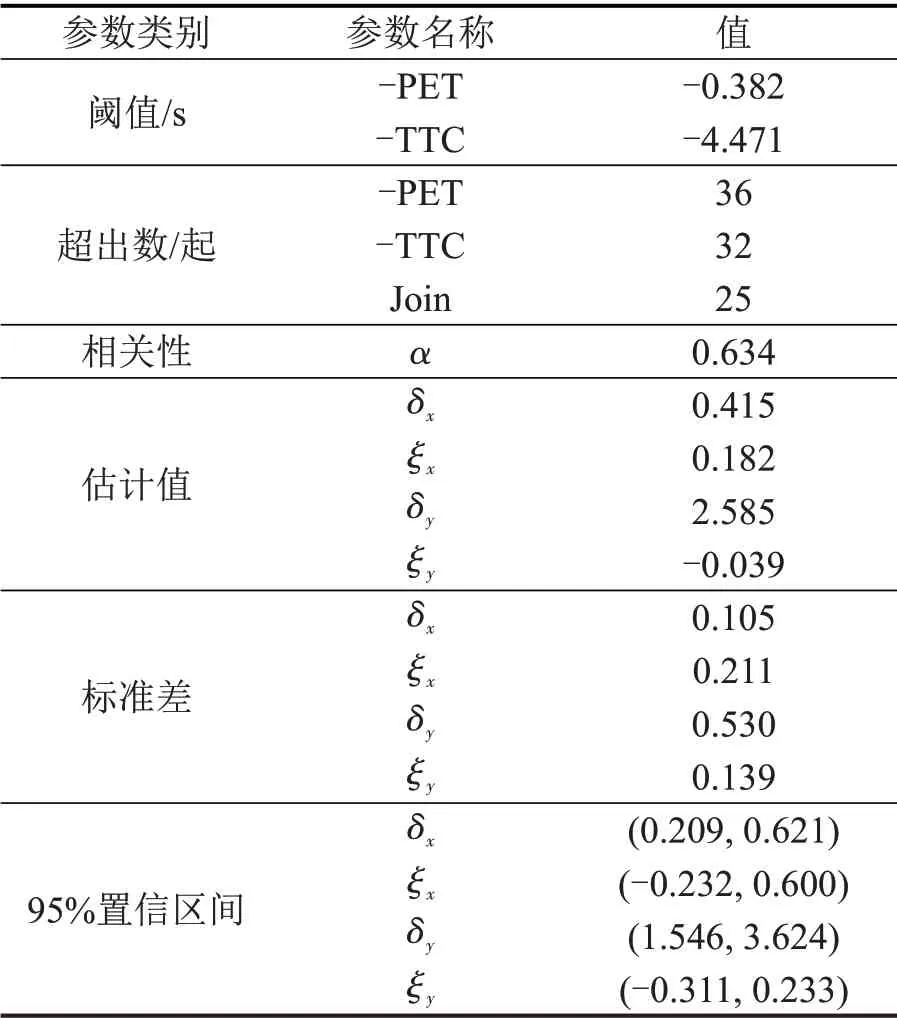
表5 BTCEV模型的参数估计结果Table 5 Parameter estimation results of BTCEV model

根据式(10)可得

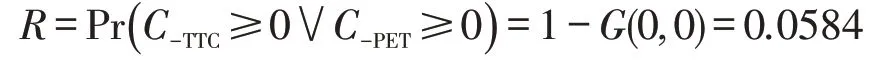
BTCEV 模型的阈值为边缘模型的阈值，即以PET等于0.382 s、TTC等于4.471 s为山区双车道公路货车严重冲突的阈值，当PET 小于等于0 s 且TTC 小于等于0 s 时，山区双车道公路货车碰撞发生的概率为5.84%，根据式(11)，山区双车道公路货车事故发生率为85.27起⋅年-1。

(2)冲突指标尾部相关性

通过BTCEV 模型估计的参数值，使用R 语言进行相关性依赖估计，可得相关性α=0.634，表明PET 和TTC 在极值水平上是渐近相关的。图9为相关性依赖函数图。

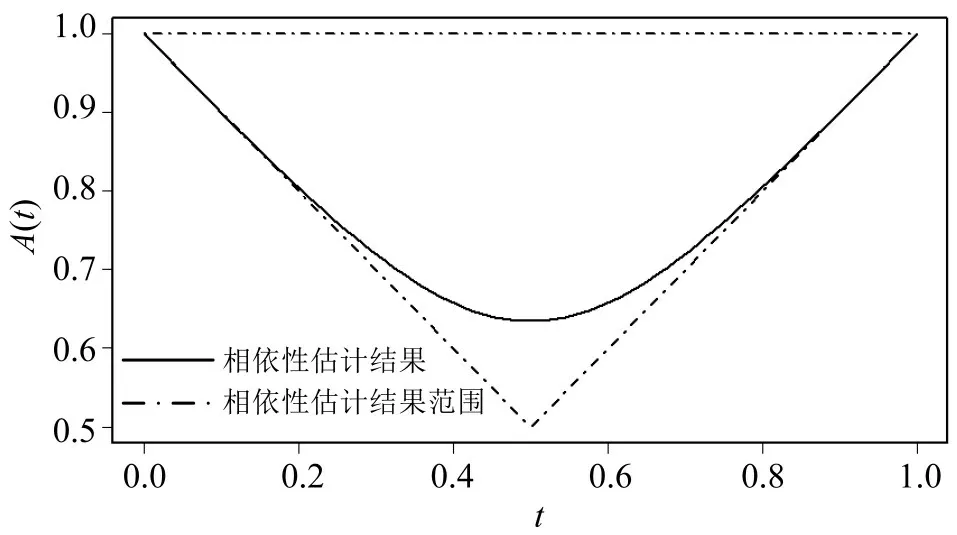
图9 相关性依赖函数图Fig.9 Correlation dependence function plot

3.4 模型结果比较

(1)预测准确率

将预测的货车年事故发生率与实际值进行对比，图10为UTCEV 模型和BTCEV 模型预测效果图。由图10可知：

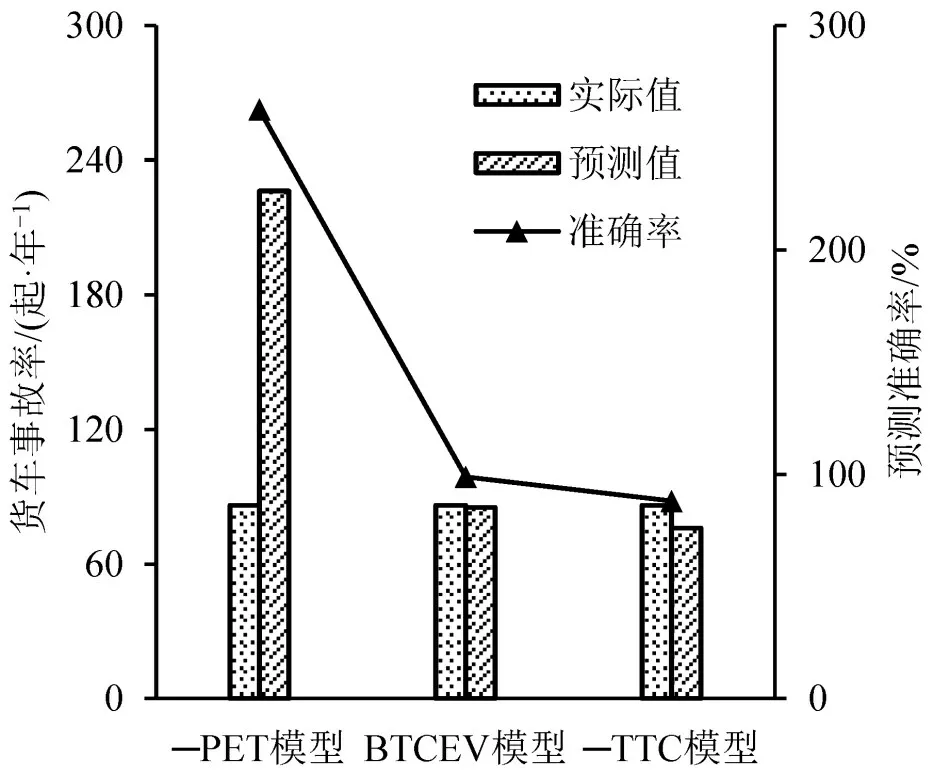
图10 UTCEV模型和BTCEV模型预测效果Fig.10 Prediction effects of UTCEV model and BTCEV model

①PET模型和TTC模型的预测准确率分别为267.34%和88.12%，预测结果存在明显的偏差。这是因为UTCEV 不能区分不同的运行轨迹，而在同等条件下，将偏移轨迹和相同轨迹视为更易发生碰撞的交叉轨迹，使得PET模型高估了山区双车道公路货车事故的发生。同理，将偏移轨迹和交叉轨迹当作相同轨迹，造成TTC模型低估了山区双车道公路货车事故的发生。

②对比两个UTCEV 模型，发现TTC 模型的预测效果明显优于PET 模型。原因是在山区双车道公路货车交通冲突中，车辆跟驰行为产生的偏移轨迹，交叉角度小，所造成的误差相对较小；而将超车行为的交叉轨迹视为相同轨迹，低估了交通事故的发生率，但其占比较小所造成的误差也相对较小。总体来看，TTC模型预测误差尚在可接受的范围。而PET将跟驰车辆的偏移轨迹视为交叉轨迹，意味着增加了交叉轨迹的观测次数，使得预测误差过大。

③BTCEV 模型预测准确率高达98.92%。由图9可知，两个冲突指标在尾部虽然相关性较弱，但显著不独立，所以UTCEV 模型预测结果存在偏差。而BTCEV模型充分考虑了山区双车道公路货车与冲突车辆的相同轨迹和交叉轨迹，并利用TTC和PET在交通安全分析上的适用性，避免了仅使用一个冲突指标所造成的偏差。

(2)模型预测精度

图11为UTCEV 模型和BTCEV 模型不同参数的置信区间比较。据图11可得，对于ξx和ξy，UTCEV 模型与BTCEV 模型估计的置信区间差别不大；对于δx和δy，BTCEV 估计的置信区间是PET模型估计的6/10，是TTC模型估计的7/10。置信区间越窄产生的预测越精确，表明利用BTCEV模型进行山区双车道公路货车碰撞预测，其预测精度明显高于UTCEV。

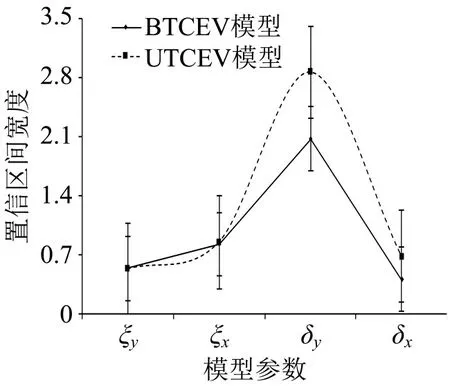
图11 UTCEV模型和BTCEV模型置信区间比较Fig.11 Comparison of confidence intervals between UTCEV model and BTCEV model

4 结论

(1)本文以山区双车道公路为研究对象，基于车辆轨迹数据，利用交通冲突理论和极值理论，构建UTCEV模型和BTCEV模型，并以云南省山区双车道公路为例，验证模型的准确性及实用性。研究发现：UTCEV 模型对山区双车道公路货车碰撞预测的结果存在明显偏差；而BTCEV 模型将货车与冲突车辆的相同轨迹和交叉轨迹纳入安全分析的统一框架，并整合了TTC 和PET 的适用性，其预测准确性和预测精度相较于UTCEV模型都有了显著提升。

(2)BTCEV 模型预测结果说明，当TTC 等于4.471 s、PET等于0.386 s时山区双车道公路货车碰撞发生概率为5.84%，预测准确率高达98.92%。本文可为山区双车道公路货车碰撞预警系统设计及事故治理提供理论依据和阈值划分标准。