铁路集装箱混合货物平衡装载布局优化模型与算法

张英贵，姚璎华，高全，雷定猷

(中南大学，交通运输工程学院，长沙 410075)

0 引言

铁路集装箱混合装运多件不同规格和不同类型的货物，其装载布局具有非对称装载、非均布载荷、重心可偏移、货物放置方式及集重制约等复杂性特征，是影响铁路集装箱及货物运输安全与效率的关键所在，科学合理的编制铁路集装箱货物装载布局方案至关重要。

目前，该领域的研究主要集中在装载布局优化目标、约束条件、空间布局方式、货物处理方式及装载布局算法设计层面。ZHU 等[1]将单箱装载布局问题求解划分为6要素，提出一种基于有效策略的贪婪算法[1]；那日萨等[2]结合实践性约束，提出一种基于块和空间的启发式算法[2]；MOURA等[3]证明了采用最大覆盖法能在较短时间内获得更好的解；张莹等[4]基于支撑面约束，提出立方体空间重叠判定和装载空间更新方法；COSTA等[5]基于负载平衡等约束，设计一种基于层排列的构造型启发式方法和货物放置角点选择策略；FANSLAU 等[6]提出一种基于同类块的复合块生成方法；ARAYA等[7]提出波束搜索策略和货物单元评价函数，通过控制变量法确定评价函数参数，以提高货物单元搜索效率。不同类型铁路货运车辆对于货物装载的要求有一定差异。朱向等[8-9]针对集装箱卡车货物装载问题考虑轴重约束，以最大化装载率和负重心偏离度为目标，设计改进贪婪自适应搜索算法，并针对铁路敞车和集重类货物，通过构造塔类货物单元，提出一种一车多件铁路集重货物装载优化方法，并未涉及高密度的非集重货物，但当该类货物装载布局分布不合理时也可能产生集重现象；雷定猷等[10]以轻重货物为研究对象，基于中心骨架思想，提出一种铁路集装箱混合平衡装载方法，并未将最大化载重量利用率纳入优化目标范畴。集装化运输是未来发展趋势，但综合国内外研究现状，对于在平衡和集重制约下装载不同规格类型的混合货物，以最大化装载空间容积和载重量综合利用率的铁路集装箱装载布局问题的研究仍有待进一步的深入，对保障货物装运安全，提升作业效率，降低物流成本具有重要意义。因此，亟需统筹考虑装载空间容积和载重量的综合利用率、装载重心平衡及集重装载等因素，结合铁路集装箱装运实际情况，提出专门面向集装箱的铁路混合货物平衡装载布局方法。

基于此，本文结合铁路集装箱装运车辆实际，给出装载重心平衡和集重容许弯矩约束量化方法，构建铁路集装箱混合货物平衡装载布局优化模型；围绕集装箱内部装载空间和待装混合货物，设计混合货物分类方法，并根据区分待装货物结构的指标构造相应类型的货物块单元，按一定方法和规则选择放置货物块及更新剩余空间，提出一种新的铁路集装箱混合货物平衡装载布局优化算法；对国际标准算例和基于标准算例生成的混合货物算例进行测试并与其他算法进行比较，验证了方法的可行性和有效性。

1 问题描述及数学模型

1.1 问题描述

铁路集装箱混合货物平衡装载布局指使用铁路集装箱装运车辆装载多件混合货物，满足装载重心平衡和集重容许弯矩等约束的前提下，最大化集装箱装载空间容积和载重量的综合利用率。该问题隶属于一车多件装载范畴，其中，混合货物具有不同品类、不同规格(重量和外形尺寸)及密度差异等特征，可以是轻重货物和集重与非集重货物等不同类型的货物。设有n类待装货物集合C={C1,…,Ci,…,Cn}，总体积为Vn，总重量为Qn，其中，第i类货物集合Ci={ci1,…,cij,…,cim} 包含m个匀质货物，总体积为Vi，总重量为Qi，单个货物长宽高分别为lij、wij、hij，体积和重量分别为vij、qij，并基于文献[10]以下的前提进行研究。

(1)待装货物外形或包装为刚性长方体，可承受重量和多层装载，不是危险品等特殊货物；

(2)待装货物有剩余时，允许留待下次装配，货物均为同一到站，途中无装卸作业；

(3)集装箱内部装载空间为长方体，装载空间的长、宽、高分别为L、W、H，有效容积和最大容许载重量分别为V、Q；以装载空间的左前内下角为坐标原点O，以车地板为X-Y平面，建立的空间直角坐标系如图1所示。

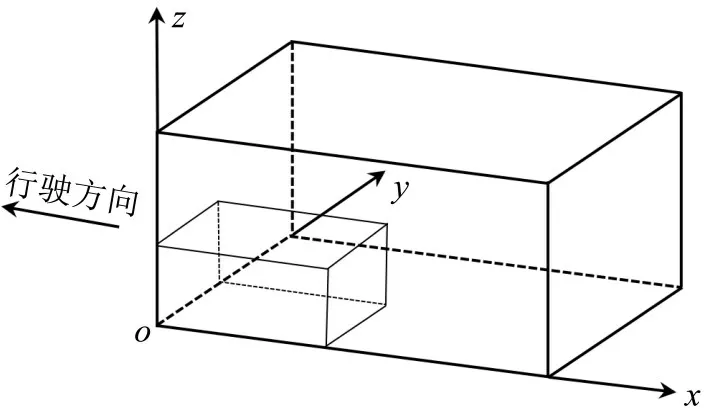
图1 空间直角坐标系示意Fig.1 Schematic diagram of space rectangular coordinate system

1.2 装载重心平衡约束分析

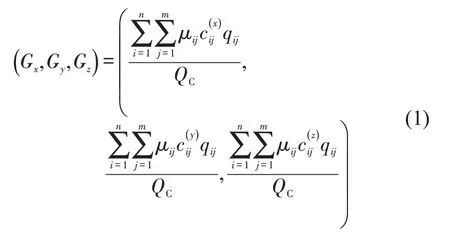
设铁路装运车辆最大容许载重量为Qmax，自重为Qv，车底架长为Lv，宽为Wv，转向架中心距为D，车地板至轨面高度为Hv，空车重心高为Ho，按照现行《铁路货物装载加固规则》[11]，货物装载后，合重心的位置投影一般应位于车地板纵横中心线的交叉点上，否则，其纵向、横向及竖直方向3个维度上分别对应的合重心纵向偏离量Δ1、横向偏离量Δ2及重车重心高Δ3必须满足一定条件：纵向偏离时，车辆转向架承重不得超过车辆容许载重量的1/2，且两转向架承重差不得大于10 t，Δ1按照计算，其中，为已装载货物总重量，Qa为集装箱自重，μij为0 或1 表示货物cij未装车或已装车；横向偏离量Δ2不得超过100 mm；重车重心高Δ3从轨面算起一般不应高于2000 mm[11]。

另以车地板左前角为坐标原点，将车辆纳入重心位置计算，如图2所示，集装箱几何中心与车地板纵横中心线交叉点重合放置，箱壁厚度为e1、e2，箱底与车地板直接接触[10]，厚度为e3，箱外壁与同侧车辆边缘距离为f1、f2，经坐标体系转化后，箱货装后，合重心坐标为

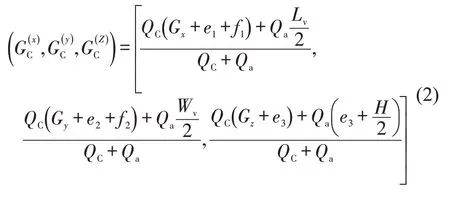
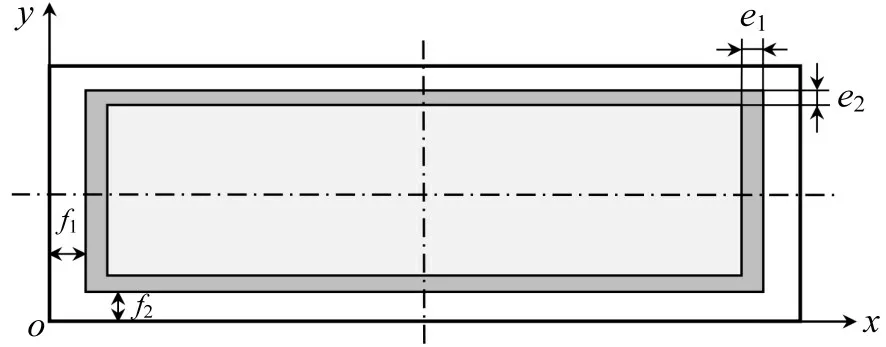
图2 装运集装箱的车辆俯视图示意Fig.2 Top view of vehicle carrying container

则箱货装后，合重心实际纵向偏离量S1、横向偏离量S2、重车重心高S3分别为

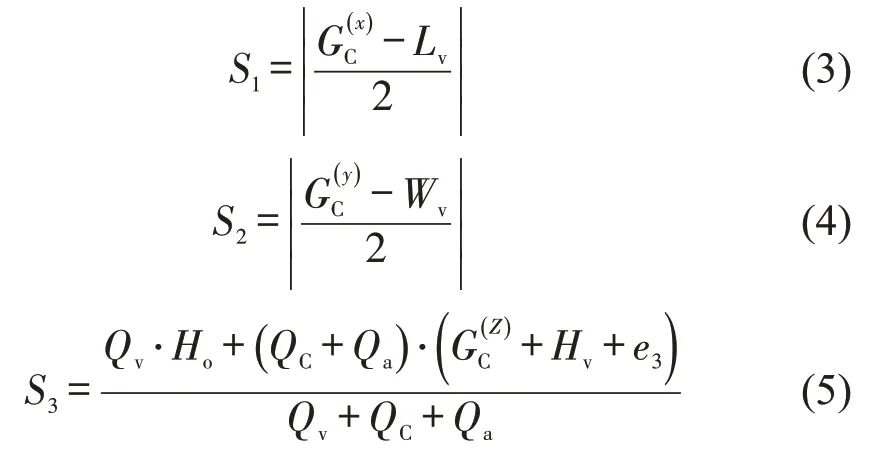
综上，对于铁路集装箱装运车辆可使用S1、S2、S3计算公式，当S1≤Δ1、S2≤Δ2、S3≤Δ3时，则满足货物装载重心平衡约束。

1.3 集重容许弯矩约束分析

当货物重量大于所装车辆负重面长度最大容许载重量，或者车辆承载构件的工作弯曲力矩大于其最大容许弯曲力矩时，将出现集重现象。对于非均布载荷，可通过分析车地板长度方向不同位置承受载荷的弯矩来度量。如图3所示，设车地板纵横中心线交点为G，前后转向架支撑点A、B产生的支撑力分别为RA、RB，位置横坐标分别为XA、XB。不同的装载布局方案有不同的货物布局形式，根据集装箱内货物单元的边界划分为N个层段L1，L2，L3，…，LN，每层段所对应的货物合重力分别为G1，G2，G3，…，GN，各合重力到车地板长度方向上任一位置x0的距离分别为X1，X2，X3，…，XN。根据力矩平衡方程，以后转向架为平衡点，可求出车地板在某x0位置所承受的弯矩为

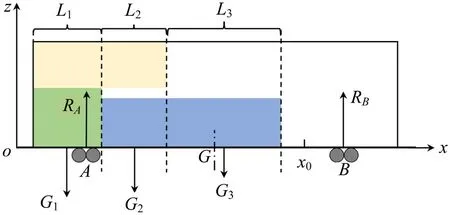
图3 车地板长度方向受力示意Fig.3 Schematic diagram of stress in length direction of vehicle floor

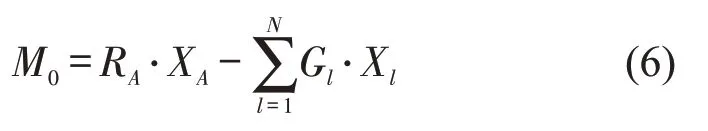
式中：N为被划分的N个层段；Gl为第l层段所对应的货物合重力；Xl为Gl到车地板长度方向某x0位置的距离。对于每一装载布局方案，按式(6)计算出车地板各处的弯矩，从而确定车地板承受的最大工作弯矩Mmax和所在位置，当Mmax不超过最大容许弯矩[M]时满足集重容许弯矩约束。

1.4 模型构建

铁路货物装载布局一般追求最大化装载空间容积和载重量的利用率，在货物装后合重心的纵向和横向偏移量满足一定要求的基础上，尽可能降低重车重心高，以确保车辆运行稳定安全。统筹考虑货物装载重心平衡、集重容许弯矩及货物放置方式等约束，以最大化集装箱装载空间容积和载重量的综合利用率为优化目标，建立铁路集装箱混合货物平衡装载布局优化模型为

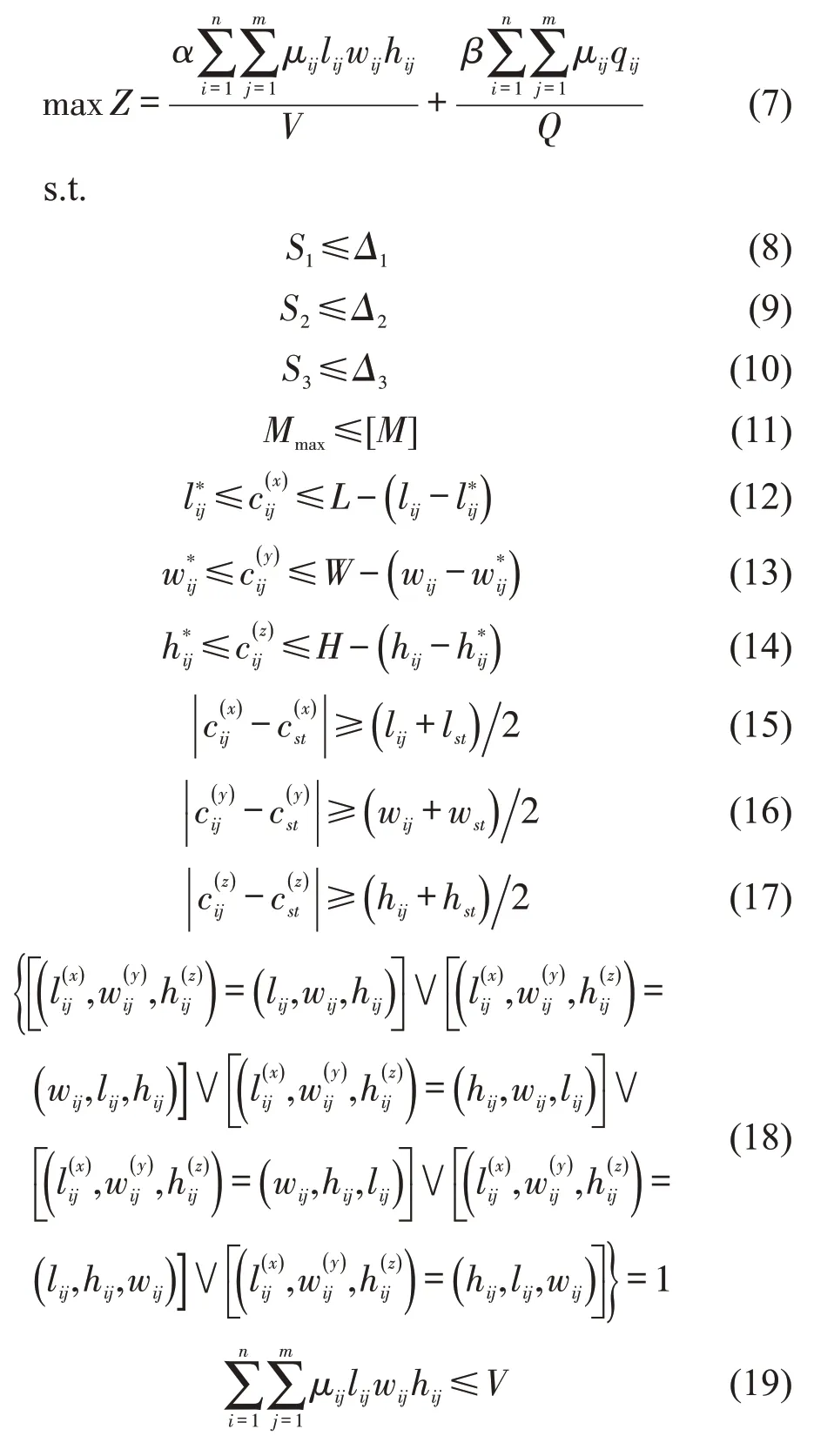
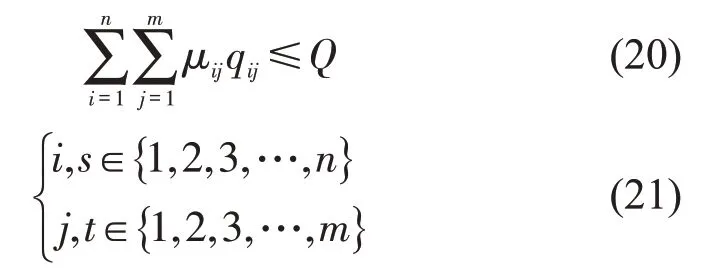
式(7)为目标函数，表示最大化集装箱装载空间容积和载重量的综合利用率，α和β为权重系数，0≤α≤1，0≤β≤1；式(8)～式(10)为装载重心平衡约束；式(11)为集重容许弯矩约束；式(12)～式(14)表示装载货物不超过集装箱边界约束，货物cij几何中心为其重心位置；式(15)～式(17)表示集装箱内任意两个货物cij和cst不能相互重叠约束；式(18)为货物的放置方式约束，表示投影在x,y,z轴方向上的尺寸长度；式(19)为集装箱装载空间容积约束；式(20)为集装箱最大容许载重量约束；式(21)为取值范围约束。

2 算法设计

铁路集装箱混合货物平衡装载布局问题隶属于装箱问题，是一个NP-Hard问题。基于货物装载布局的过程[1]，从货物单元的构造、选择及放置，剩余空间的表示、选择及更新等方面设计算法。为缩短求解时间并提高解的质量，采用最大覆盖法[3]表示剩余空间；便于产生更多有效剩余空间和减少碎片空间，采用曼哈顿距离[1]选择剩余空间。在此基础上，不同于直接将货物构造为货物块的方法，本文设计了混合货物分类方法，并根据区分待装货物结构的指标判断问题类型，构造简单或复合块单元，将货物块单元选择评估函数与贪婪d步前瞻树搜索结合起来选择货物块单元，设计货物块单元放置与剩余空间更新规则，提出一种新的铁路集装箱混合货物平衡装载布局优化启发式求解算法。

2.1 混合货物分类方法

基于生成块单元的方法被证明是解决装箱问题最有效的方法[12]。在对混合货物进行分类的基础上，采用文献[12]中的方法，生成不同类别的货物块单元。

混合货物的重量、体积及密度差别较大，属性较为复杂，以货物泡重比1∶g1和1∶g2为标准，即以1 m3货物的重量值g1、g2为界，结合货物的重量、体积及密度，将混合货物划分为重货、平货及轻货，具体方法如下：

算法2.1 混合货物分类算法

输入为混合货物集合C；

输出为重货集合CK，平货集合CF，轻货集合CS。

Step 1 确定重货集合。将货物按类重量降序排列，若重量相同，则将货物类个数较少的排在前面，取前Ka1=0.5nc1+1 类，nc1为货物集合C总类数量；对于前Ka1类货物再按密度降序排列，若密度相同，则将货物类个数较少的排在前面，设该排列为CK1,CK2,…,CKa1；然后找到Ka2使得{CK1,CK2,…,CKa2} 的类货物密度均大于g1kg⋅m-3。

Step 2 返回重货集合CK={CK1,CK2,…,CKa2}。

Step 3 确定平货集合。将重货从货物集合C中删去，余下货物按类体积降序排列，若体积相同，则将货物类个数较少的排在前面，取前Fa1=0.5nc2+1，nc2为除重货外剩余货物的类数量；对于前Fa1类货物再按密度降序排列，若密度相同，则将货物类个数较少的排在前面，设该排列为CF1,CF2,…,CFa1；然后找到Fa2使得{CF1,CF2,…,CFa2}的类货物密度大于g2kg⋅m-3。

Step 4 返回平货集合CF={CF1,CF2,…,CFa2}。

Step 5 确定轻货集合。将重货和平货从货物集合C中删去，然后，按类密度降序排列，得到轻货集合

2.2 货物块单元选择算法构造

考虑待选货物块b的体积V(b)、货物个数N(b)及重量W(b)，以及直接接触或间接投影覆盖率C(b,p)和空间损失率L(b,r)这5 个因素[10]，构造铁路集装箱混合货物平衡装载布局货物块单元选择评估函数为

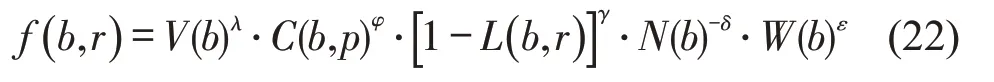
其中，间接投影覆盖是指间距小于参数p与其所在坐标轴方向上货物块尺寸lb乘积的投影区域，如图4所示；空间损失率为用剩余货物块对b的3个坐标轴方向分别求一维背包问题后得到的剩余浪费空间体积与原空间r体积的比值，如图5所示。L(b,r)和N(b)越小，其他3 个因素越大，则货物块单元b的评估函数值越高，易被优先选择。

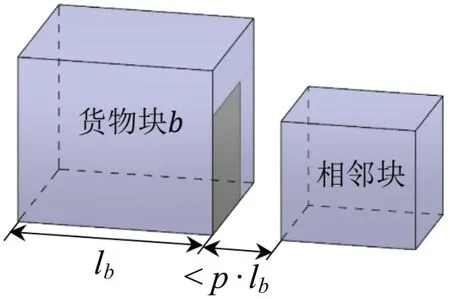
图4 间接投影覆盖示意Fig.4 Schematic diagram of indirect projection coverage

图5 空间损失示意Fig.5 Schematic diagram of space loss

结合货物块单元选择评估函数，构造基于贪婪d步前瞻树搜索的货物块单元选择算法：

算法2.2 货物块单元选择算法

输入为货物块单元集合，空间集合R，当前布局空间r，货物块单元选择评估函数参数λ、p、φ、γ、δ、ε，搜索树宽度系数u，搜索树深度系数d。

输出为当前布局空间选择的货物块单元b。

Step 1 初始化。d=0 时，根节点P表示初始状态，即当前的布局空间r，仅考虑从剩余空间集合中选择1个布局空间进行决策，不考虑同时选取多个空间进行决策的情况。

Step 2 第1 层树搜索。d= 1 时，选取评估函数值排在前u的货物块单元生成搜索树第1 层的u个子状态，每个子状态表示1 个不完全装载布局方案。

Step 3 多层树搜索。对于每一层搜索树，每个节点均选择评估函数值排在前u的货物块单元生成u个子状态，由于不同的货物放置方式有不同的评估值，若同一货物块单元在多种放置方式下的评估函数值均排在前u，则此货物块单元被选取多次；第d层的每个叶节点表示1个完整的装载布局方案，所有叶节点产生w=ud个方案。

Step 4 选择货物块单元。w个方案中生成最好解的第1 个货物块单元即为当前阶段应放置的货物块单元，返回当前布局空间r选择的货物块单元b。以d=2，u=3 时的情况为例，如图6所示，若加粗路径为最好装载布局方案，则货物块单元b2为本次应放置的最合适货物块。

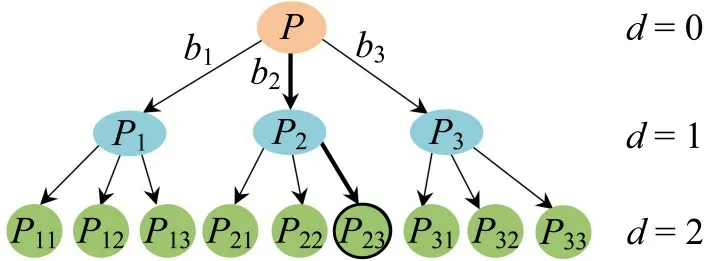
图6 基于贪婪d 步前瞻树搜索的货物块单元选择示例Fig.6 Example of goods block unit selection based on greedy d-step forward looking tree search

2.3 货物块放置与空间更新规则

考虑到装载重心平衡及集重容许弯矩约束，先放置对货物装后合重心位置影响较大的重货块，再分别放置对合重心位置影响较小的平货块和轻货块，当出现货物布置完、无可用布局空间及货物总重量不满足最大容许载重量约束时，则结束布局。其中，货物块放置方式为其包含的所有货物放置方式的交集。该放置方法将货物连续地由集装箱装载空间角向中部进行布局，增加了重货放置在靠近装载空间角位置的机会，使重量或密度较大的货物分布于接近车辆转向架两边的位置，中间位置的货物重量相对较轻，更符合车辆承受载荷能力分布规律。

当货物块放入某一布局空间后，将使用最大覆盖法生成的3个新空间放入空间集合中，删去原布局空间、尺寸为零、重复及被其他极大空间包含的空间，并判断空间集合中现存空间与放入货物块的重叠情况，将货物块与空间重叠的部分删去，用最大覆盖法重新划分与货物块重叠的空间，将生成的新空间放入空间集合中，货物块与空间重叠情况具体如下：

(1)货物块与空间有1个角重叠的情况有8种，图7为其中一种，使用最大覆盖法可将原重叠空间划分成3个新空间。

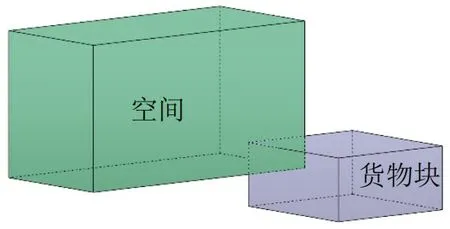
图7 货物块与空间有1角重叠的一种情况Fig.7 A situation in which a block overlaps a corner of space

(2)货物块与空间有2 个角重叠的情况有24种，其中，货物块2 个角同时位于空间中的情况有12种，每种可生成4个新空间；空间2个角同时位于货物块中的情况有12种，每种可生成2个新空间。

(3)货物块与空间有4 个角重叠的情况有12种，其中，货物块1个面上4个角位于空间中的情况有6 种，每种可生成5 个新空间；空间1 个面上4 个角位于货物块中的情况有6 种，每种可生成1 个新空间。

(4)货物块与空间包含重叠的情况有2 种，其中，货物块全在空间中的情况有1种，可生成6个新空间；空间全在货物块中的情况有1 种，应删去此空间。

(5)货物块与空间交叉重叠的情况有18 种，其中，货物块沿坐标轴方向从空间边界贯穿的情况有12 种，每种可生成3 个新空间；货物块沿坐标轴方向从空间中部贯穿的情况有3 种，每种可生成4 个新空间；货物块将空间分割成两部分的情况有3种，每种可生成2个新空间。

2.4 装载布局算法设计

综上，铁路集装箱混合货物平衡装载布局优化启发式求解算法如下：

算法2.3 铁路集装箱混合货物平衡装载布局优化算法

输入为空间集合R，混合货物集合C，运行时间T，货物块单元选择评估函数参数λ、p、φ、γ、δ、ε，搜索树宽度系数u，搜索树深度系数d。

输出为装载布局方案Sbest。

Step 1 货物分类。调用算法2.1，将混合货物集合C分成重货、平货及轻货3类货物集合。

Step 2 生成货物块单元。引入一个区分待装货物结构的指标t，，当t＞6 时，问题类型为弱异构类问题，调用文献[12]中的简单块构造方法分别生成重货、平货及轻货集合的简单货物块单元集合；当t≤6 时，问题类型为强异构类问题，调用文献[12]中的复合块构造方法分别生成重货、平货及轻货集合的复合货物块单元集合。

Step 3 选择并放置货物块。根据曼哈顿距离确定锚距，从空间集合R中选出锚距最短的空间作为待布局空间r，初始布局空间为集装箱原内部空间。调用算法2.2 选取重货块，将其放置在待布局空间r的锚角处，并按本文空间更新规则对空间集合进行更新；同理，若重货已被放置完，当空间集合中还有剩余空间和货物总重量满足最大容许载重量约束时，则继续依次选取平货块和轻货块进行放置，直至待装货物均被放置完、空间集合中无可用空间或货物总重量超出最大容许载重量。

Step 4 生成装载布局方案。输出1个装载布局方案s，检查s是否满足装载重心平衡约束和集重容许弯矩约束，若不满足装载重心平衡约束，则归入装载不平衡方案集合S′中，若不满足集重容许弯矩约束，则放入集重方案集合S″中，转Step 5；若均满足，则与目前得到的最好方案进行比较，将较好者记为Sbest，转Step 5。

Step 5 加倍迭代搜索。若在每次迭代后还有剩余时间，则进行加倍的贪婪d步前瞻树搜索，令w=2w，，即重新生成不同的新布局方案；否则，转Step 6。

Step 6 返回最优方案Sbest。

3 算例分析

由BISCHOFF等[13]和DAVIVE等[14]提出的用于评估装载问题算法的1600个算例被认为是国际标准算例，编号从BR0～BR15 共有16 组，每组有100个算例，货物种类从BR0的1类增加到BR15的100类，每类货物的数量从BR0 的50.15 个左右减少到BR15 的1.33 个左右，其中，BR0 为同质类问题，BR1～BR7为弱异质类问题，BR8～BR15为强异质类问题。在此标准算例的基础上，RAMOS 等[15]考虑了货物重量，设定货物密度区间为，其中，为待装货物的平均密度，E[x]为贝塔分布期望，按照f(x,2,5)得到算例货物密度。为验证所提方法的可行性和有效性，采用同样考虑货物重量的标准算例进行测试，使用某铁路货运车辆及集装箱进行装运，相关参数为：Lv=13000 mm，Wv=2980 mm，D=9000 mm，Hv=1212 mm，Qmax=60 t，Qv=22.4 t，集装箱内部装载空间尺寸L=5870 mm，W=2330 mm，H=2200 mm，Q=28.1 t，Qa=2.3 t，e1=94 mm，e2=54 mm，e3=120 mm，由于陆运货物泡重比未有统一标准，参考其他运输方式泡重比标准并结合铁路运输实际，混合货物分类算法中的g1取为300 kg⋅m-3，g2取为167 kg⋅m-3。利用控制变量法确定货物块单元选择评估函数中参数λ和ε的值分别为0.6、0.2，搜索树深度系数d取2，其他参数值选用ARAYA等[7]确定的φ=4,γ=1,δ=0.2,p=0.04。测试电脑处理器为Intel(R)Core(TM)i7-8565U CPU @1.80 GHz，内存为8 GB，运行系统为Windows10(64位)，算法通过Java 语言实现(JDK1.8 版本，64 位)，并用Eclipse软件(Oxygen版本)进行编译。

3.1 国际标准算例对比分析

基于上述参数，分别构造简单货物块和复合货物块测试国际标准算例。设定1600个算例的平均运行时间在100 s 左右(±10 s)，在每次迭代后进行加倍搜索，得到测试结果如表1所示，其中，平均运行时间为1600 个算例运行的平均时间，数据结果为同组100个算例结果的平均值，Vol.表示容积利用率，Wt.表示载重量利用率，Sum.表示综合利用率，Unb.和WtC.分别表示在不低于某一综合利用率平均值时不满足装载重心平衡约束和集重容许弯矩约束的算例数量，其值越低越好。

通过对比在国际标准货物算例测试下得到的SB 和GB 两列结果可以发现：构造复合货物块时，BR1～BR15的集装箱平均容积利用率、载重量利用率及综合利用率均比构造简单货物块时高；对于同质类货物BR0 和弱异质类货物BR1～BR7，构造简单货物块时的结果优于复合货物块；但对于强异质类货物BR8～BR15，构造复合货物块时的结果则优于简单货物块。根据待装货物的结构指标t来判断BR0～BR15 的问题类型与其实际问题类型完全相符，可见根据指标t对待装货物构造不同的货物块单元，可以选择更有优势的货物块单元类型，从而得到更好的结果。

在使用国际标准算例及构造复合货物块单元的相同条件下，与雷定猷等[8]提出的轻重货物混合平衡装载算法对比可知，本文所提方法的集装箱平均容积利用率更高，主要是因为所提方法在每次选择货物块单元时，选择在当下布局会使最终方案利用率最高的最合适货物块，在货物块放置时，将碎片空间尽可能地集中在集装箱装载空间中部，保证了货物与货物间的装载紧密性；另外，所提方法考虑了载重量利用率和综合利用率的情况，也能达到较好装载效果；根据“Unb.”和“Wtc.”可推算出，对于国际标准算例，所提方法在保证集装箱平均容积、载重量及综合利用率分别不低于91%、85%、88%的同时，装载重心平衡、集重容许弯矩约束满足概率能达99.33%、99.73%以上，结果可观；同时，通过测试发现，当货物装后合重心有所偏移且在许可范围内时，适当的纵向偏移有助于降低车地板承受的弯曲力矩，避免产生集重。

3.2 基于标准算例生成的混合货物算例对比分析

为进一步了解所提方法对于重量、体积及密度等差异更大的混合货物的应用效果，在国际标准算例的基础上，将货物边长尺寸区间增大为(20,200)mm，同时，增设货物重量区间(50,500)kg，以贝塔分布f(x,0.75,0.75)确定货物尺寸和重量，以集装箱装载空间容积和最大容许载重量为限，共同确定各类货物数量，生成货物尺寸、重量及密度差异较大的混合货物算例，分别对BR0～BR7 构造简单货物块，对BR8～BR15 构造复合货物块，测试结果如表1所示。

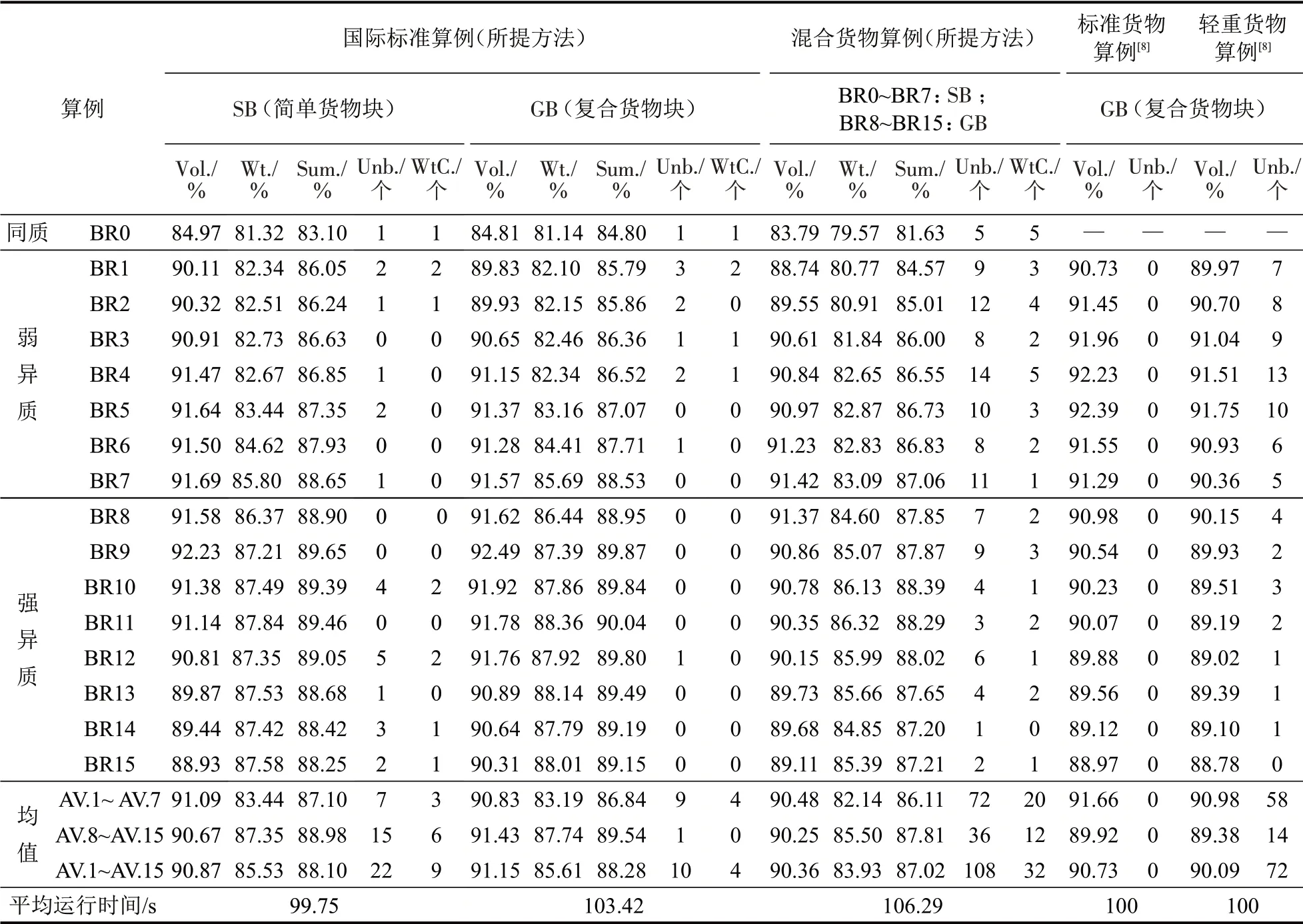
表1 不同算法和不同算例的测试结果Table 1 Test results of different algorithms and different examples

对比所提方法在国际标准算例下GB 列的测试结果，由于混合货物的属性复杂度增加，所提方法对于混合货物算例测试得到的集装箱平均容积利用率、载重量利用率及综合利用率有所下降，但仍能达到较好的装载效果；对比轻重货物混合平衡装载算法测试轻重货物算例时的结果[8]，所提方法平均容积利用率略高，在保证集装箱平均容积利用率不低于90%的同时，装载重心平衡约束满足概率相差不大，但在集重容许弯矩约束满足概率方面表现良好。所提方法能够在保证集装箱装载空间平均综合利用率不低于87%的同时，有92.8%、97.87%以上的概率满足装载重心平衡和集重容许弯矩约束。总之，所提方法得到的货物装载方案对于集装箱的利用效果较好，能够在实现较高集装箱利用率的同时较好保证混合货物平衡装载。

4 结论

针对铁路集装箱混合货物平衡装载布局问题，量化装后合重心平衡和集重容许弯矩约束，以装载空间容积和载重量综合利用率最大为目标，建立了一种改进的铁路集装箱混合货物平衡装载布局优化模型，并基于空间和货物属性设计一种新的优化算法。主要结论如下：

(1)设计的基于混合货物分类方法和待装货物结构判断指标的货物块单元构造方法，能针对性地构造更具优势的货物块类型；设计的货物块选择算法、放置及剩余空间更新规则，能有效提高货物块与剩余空间的适配度，减少空间浪费。

(2)所提方法在保证集装箱装载空间容积和载重量的平均综合利用率不低于87%的同时，有92.8%、97.87%以上的概率满足装载重心平衡和集重容许弯矩要求，能够客观全面地反映装载空间利用情况并达到平衡装载的要求，确保铁路集装箱混合货物平衡装载。