灵活编组条件下轨道交通客货协同运输方案优化

戚建国，周厚盛，杨立兴，周亚茹，张春田

(北京交通大学，轨道交通控制与安全国家重点实验室，北京 100044)

0 引言

随着城市化进程的不断加快和城市机动车保有量的不断增加，道路交通拥堵和环境污染问题日趋严重。为缓解道路交通压力，大力发展城市轨道交通，充分利用地下空间资源成为交通部门缓解交通问题的重要举措[1]。在轨道交通快速发展的同时，如何有效地利用轨道交通资源提供高质量运输服务，是轨道交通运营部门和相关学者关注的重点。

针对轨道交通客流需求随时间变化呈现出的动态性和在空间分布上呈现出的不均衡性的特点，广大学者一直致力于从不同的角度开展轨道交通运营组织优化方面相关研究，以实现客流与车流的良好匹配。YIN等[2]考虑客流需求的动态性和随机性，从优化运营供给方面出发，采用近似动态规划算法求解运行图优化问题，在降低列车能耗的基础上，实现车流和客流的良好匹配。SHI 等[3]从运营供给和需求管理两方面出发，针对部分线路某些车站存在过饱和大客流的情况，构建列车运行图与客流控制协同优化模型，并利用局部搜索算法结合CPLEX 优化软件求解模型，以降低乘客的等待时间。为更好地应对客流在时间和空间分布上的不均衡性问题，许多学者进一步研究了大小交路、停站策略等多种不同运营组织模式在实际中的应用。例如，许得杰等[4]针对时变客流需求，考虑大小交路运营组织模式，构建城市轨道交通大小交路列车运行图优化模型，并利用遗传算法求解模型，提高了客流与车流的匹配程度。孟凡婷等[5]基于跳停策略，研究列车运行图与客流控制协同优化问题，构建线性混合整数规划模型，并利用CPLEX 求解模型。

虽然上述研究为城市轨道交通的高效运行提供了良好的理论支撑，但大多是针对固定编组模式开展客运相关研究，考虑灵活编组模式的相关研究较少。目前，针对灵活编组模式的研究，大多集中于灵活编组模式可行性[6-7]及开行方案优化问题，较少集中于基于灵活编组的列车运行图优化问题研究。考虑到灵活编组模式对客流不均衡分布良好的适应性，禹丹丹等[8]基于灵活编组策略，研究城市轨道交通列车开行方案优化问题，并提出了四阶段求解方法，以降低乘客广义出行成本和企业运营成本。另外，鉴于电子商务的快速发展及部分地铁线路出现运能过剩的现象，许多学者开始呼吁发展地下物流系统，以充分利用地下空间资源。但相关研究仍处于起步阶段，部分学者主要针对地下物流系统可行性、运输方式以及系统布局等方面开展研究[9]，针对轨道交通客货协同运输组织优化相关研究较少。

鉴于此，本文基于灵活编组运营组织模式，在充分保障乘客运输服务质量的基础上，考虑客流和货流之间的竞争关系，开展客货协同运输组织优化研究，构建基于灵活编组的轨道交通客货协同运输方案优化数学模型，以保障轨道交通乘客运营服务质量与企业运营效益的双向利益。

1 问题描述

本文以客流未饱和的单条轨道交通线路为研究对象，并假定线路的两端均存在车辆段且均可对列车进行拆解和重联。本文通过给出编组类型集合的方式考虑多种列车编组类型，同一列车可以为单一的客运列车或者货运列车编组，也可为客货混合列车编组，并且存在多种类型列车编组长度，如图1所示。

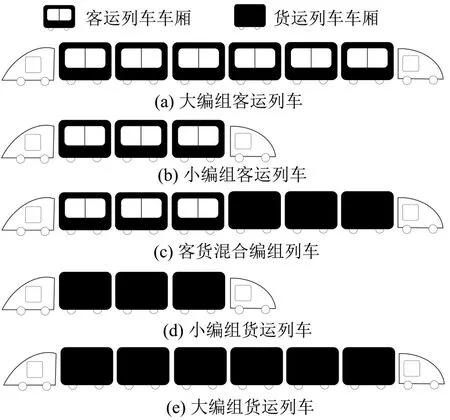
图1 轨道交通列车灵活编组模式示意图Fig.1 Schematic diagram of flexible marshalling operations

基于给定的列车编组类型集合，本文针对动态客货运输需求，充分考虑列车运行安全和不同编组类型列车容量，以确定每一列车的具体编组类型和每一列车的发车间隔为主要决策，以对应客流和货流在每一列车上的分配为辅助决策，从时间和空间两方面对轨道交通客流和货物运输进行协同优化，实现轨道交通客流、货流与车流的良好匹配。

2 模型构建

2.1 模型假设及参数定义

为构建严格的数学优化模型，本文针对客货协同运输优化问题给出如下基本假设：

假设1 只考虑单方向的列车运行情况，且列车只能在车辆段内进行解编与重联操作。

假设2 假定客流与货流需求均为已知，且在运营过程中不会发生转移，即客流和货流需求总量不发生变化。

假设3 针对列车运能充足的条件下开展客货协同运输研究，所有运输需求均保证被满足，且客流运输不允许存在二次等待的情形，但允许货物存在等待和提早发货的情况。

假设4 假定所有货物均提前按出发地及目的地装入标准货运箱，并且只有部分备选车站允许进行货物运输。

为便于描述，本文模型所涉及符号和参数及其相关定义如表1所示。

表1 符号和参数的表示方法及定义Table 1 Definition of symbols and parameters

本文构建模型的决策变量包括：

(1)列车运行图相关决策变量及中间变量

hk——列车发车间隔，表示前车k与后车k+1的发车间隔；

——列车到站时刻，表示列车k到达车站i的时刻；

——列车离站时刻，表示列车k离开车站i的时刻；

zk,i(t)——列车离站与否指示变量，表示列车k在t时刻是否已从车站i离开，是为1，否则为0；

dk,i(t)——列车离站指示变量，表示列车k在t时刻是否离开车站i，是为1，否则为0；

bk,i(t)——列车有效乘车时间指示变量，表示t时段内到达车站i的客流及货流是否可能乘坐列车k，是为1，否则为0。

(2)列车编组相关决策变量

yk,m——0-1 决策变量，表示列车编组类型选择，当列车k选择m类型编组为1；否则，为0。

(3)客流及货流分配相关决策变量及中间变量

，——列车k离开车站i时的载客量和载货量；

，——列车k离开车站i时的上客量和装货量；

——列车k离开车站i时以车站j为目的地的装货量；

，——列车k到达车站i时的下客量和卸货量；

——时刻t在车站i等待的客流需求。

2.2 目标函数

本文拟以客流未饱和线路为基础，在客流运输服务的基础上开展货物运输服务，以期在保证较高发车频率基础上(降低乘客等待时间)充分利用轨道交通运能。由于本文仍以客流运输为主，不允许乘客存在二次等待及客流转移的情形。为了在客流运输服务质量得到保证的基础上，尽可能充分利用列车剩余容量，本文模型的优化目标为极小化乘客等待时间和列车总运营成本(运营收益减去运营成本)。由于本文假定不存在乘客二次等待的情况，故乘客等待时间可表示为所有离散时间区间内等待乘客数量与离散时间区段长度乘积的总和，即

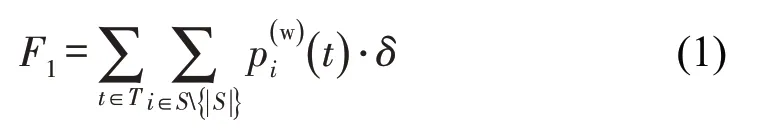
客货共运模式下的运营收益主要包括乘客和货物票价运输收益；运营成本为不同类型编组列车被选择投入运营的成本之和，运营成本与运营收益之差为

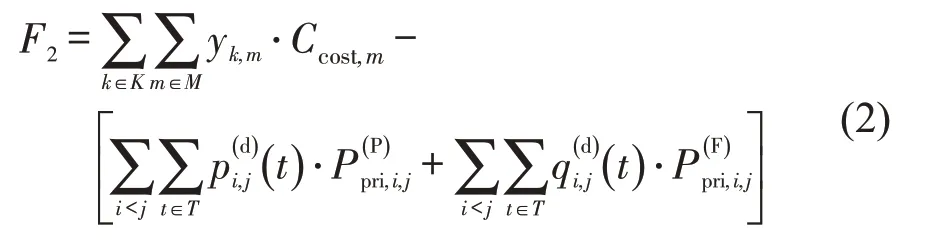
由于本文假定所有的客货运输均需得到服务，在票价固定的情况下，运营收益为一固定的常量，故式(2)可进一步简化为

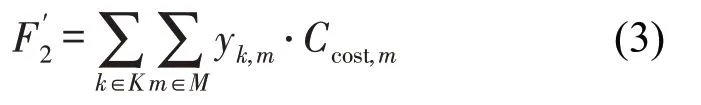
为便于模型的求解，本文通过引入乘客等待时间成本并结合加权平均系数ω1，ω2来处理双目标优化问题，得到的目标为

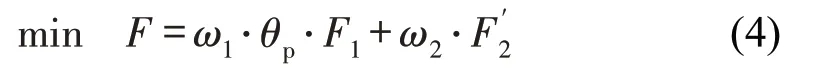
式中：θp——乘客单位等待时间成本费用，具体取值一般与乘客对等待时间的敏感度有关，对于等待时间敏感的乘客可取较大的值。

2.3 模型约束条件

(1)列车时刻表相关约束

为保证列车的运营安全，并确保必要的服务水平，列车的发车间隔需控制在一定的范围内，本文的列车发车间隔时间约束为

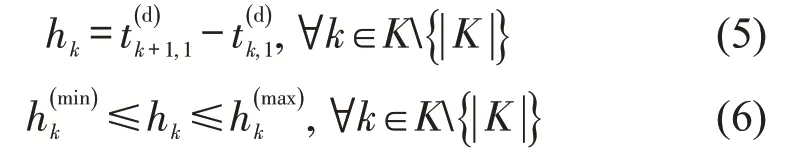
本文假定列车的区间运行时间和在站停靠时间均为固定值，列车在每一座车站的到、发时刻与其在该车站的停靠时间和站前区间运行时间存在的关联约束为

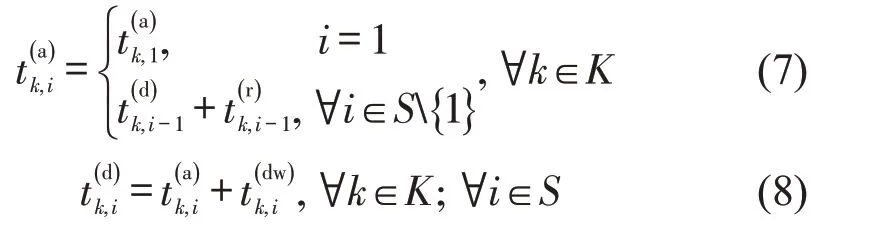
为了能清晰地描述客流及货流动态加载过程，本文引入指示列车离开车站与否的0-1辅助指示变量zk,i(t)，列车离开车站时刻的0-1 辅助指示变量dk,i(t)，以及列车在站有效乘车时间的0-1辅助指示变量bk,i(t)。各变量之间存在的关联约束为

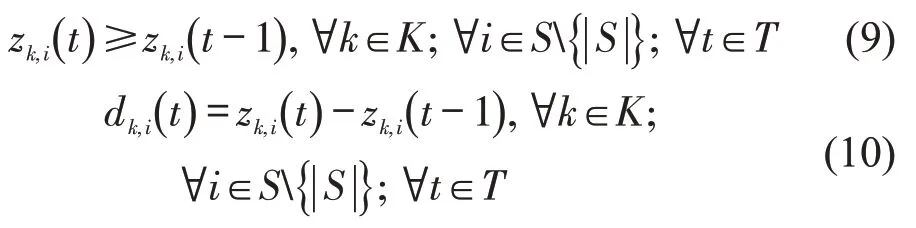
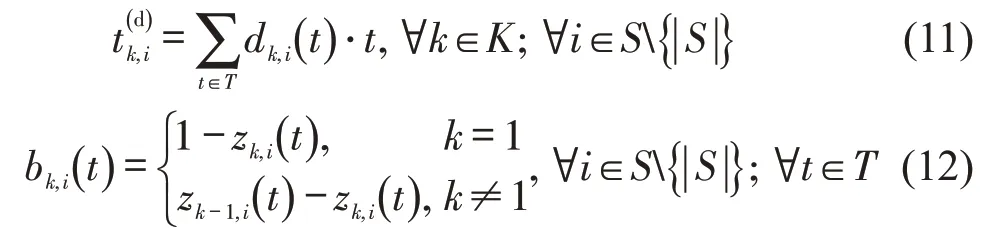
式(9)为变量zk,i(t)存在的非减特性；式(10)和式(11)为指示变量zk,i(t)与列车离站时刻变量之间的耦合关系；式(12)构建了列车在站有效乘车时间指示变量bk,i(t)与列车离站与否指示变量zk,i(t)之间的关联约束。

(2)列车灵活编组相关约束

为实现列车运能与客货需求之间的良好匹配，避免出现能力浪费和过度拥挤的情况，本文假定车辆段可对不同的客运车厢与货运车厢进行解编与重联，且存在多种编组类型列车。然而，由于受现实列车长度的限制，灵活编组类型通常是有限的。本文通过给定编组类型备选集合的方式来确保编组类型的可行性，因而，每一列列车在开始运行时即要确定执行该次服务的列车编组类型。为确保每一服务列车只能选择一种编组类型，本文给出列车灵活编组类型选择约束为

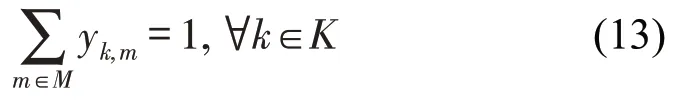
(3)客流及货流加载相关约束

由于本文拟充分利用轨道交通客运剩余能力并结合灵活编组运营组织模式开展货物运输，为确保客流需求均能得到必要的运输服务，且客流不存在二次等待的情况，给出客流需求相关约束为

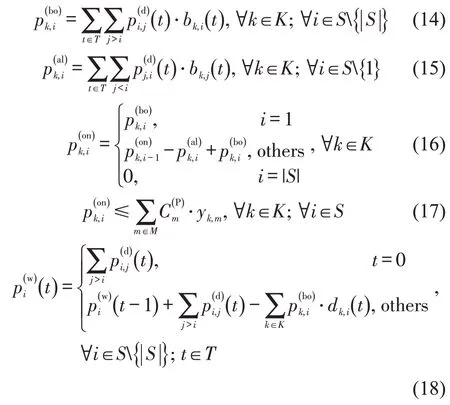
式(14)和式(15)确保到达乘客均可乘坐其到达车站后第一列离开的列车，并构建了到达客流与上、下车客流之间的关联约束；式(16)构建了列车k离开车站i时的载客量与上、下车客流之间的关联约束，并可进一步帮助构建列车容量约束式(17)，以确保列车运营安全；式(18)为等待乘客数量与到达客流数量及上车乘客数量之间的关联约束，表示t时刻在车站i等待乘客数量等于t-1 时刻等待的乘客数量与t时刻到达乘客之和减去上车离开乘客数量。

本文基于灵活编组的运营组织模式，开展客货协同运输，以期充分利用轨道交通运力，在不影响乘客运输服务质量的同时，增加由于开展货运运输带来的收益。由于客流与货流之间存在一定的竞争关系且对列车编组类型的选取具有重要的影响，本文允许货物运输存在一定的运输延迟，即货物运输存在二次等待甚至多次等待的情形，并且允许货物提前进行运输。同时，为确保货物运输必要的服务质量，本文假定所有的货物运输均需得到满足，构建的货流需求约束为

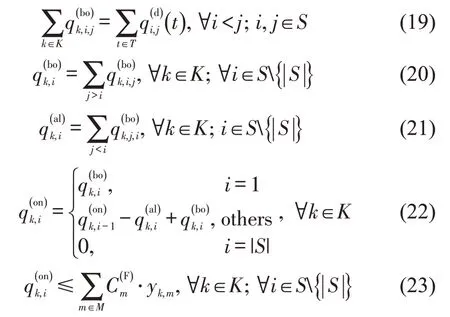
式(19)确保了所有的货物需求均能得到满足；式(20)表示站点装载货物数量等于对应从该车站出发去往其余车站装载货物量之和；式(21)表示站点卸载货物数量为以该站点为目的地的装载货物数量之和；式(22)和式(23)构建了在车货物数量与装载和卸载货物数量之间的关系，并确保列车载货数量不能超过灵活编组列车货物运输能力。

2.4 模型线性化及求解方法

由于式(18)中存在整数变量与0-1变量相乘的情形，为典型的非线性约束。为便于求解，本文借鉴文献[10]中提出的定理，对式(18)进行线性转换。

定理：连续变量x∈[0,u]与0-1变量y∈{0,1} 的乘积x⋅y，可通过引入一个新的连续变量z=x⋅y来代替，当且仅当新引进连续变量z满足如下两个条件：(1)当y=1 时，z=x；(2)当y=0 时，z=0。因此，z需要满足的条件为

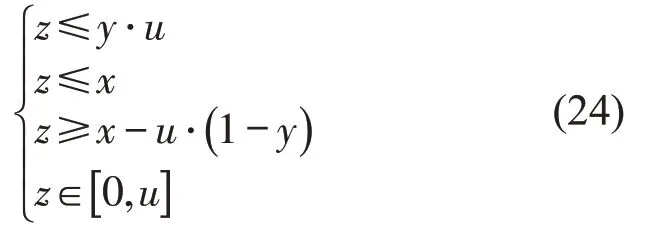
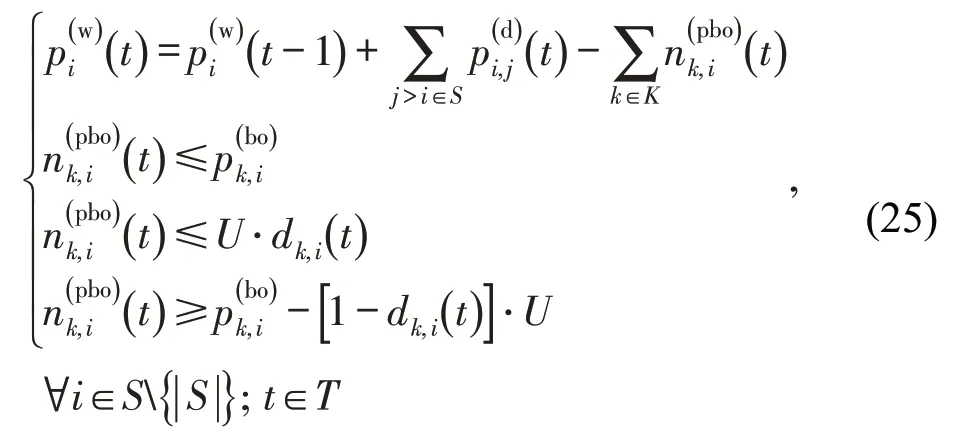
综上，本文构建基于灵活编组的轨道交通客货协同运输线性混合整数规划模型，可利用CPLEX或GUROBI等商业优化软件进行求解。

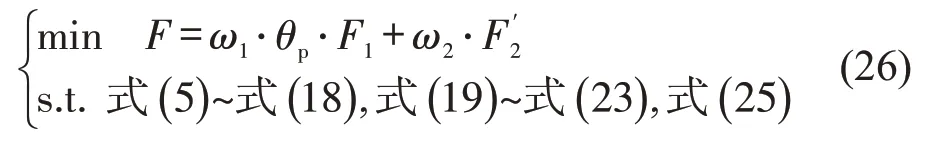
3 实证研究

3.1 基础数据

本文以北京地铁八通线上行方向(四惠-土桥)为研究对象(共13 座车站)，结合自动售检票系统(AFC)历史刷卡数据，选取研究时段为工作日上午8:00-11:00，设置离散时间长度为1 min，共有180个时间区段的客流需求数据。

本文考虑35 列列车，5 种编组类型，分别为大编组客运列车(L-P-T)、小编组客运列车(S-P-T)、客货混合编组列车(P-F-T)、小编组货运列车(S-F-T)和大编组货运列车(L-F-T)，假设其对应的运营成本和列车容量(乘客容量和货物容量)分别为{10000，8000，9000，7000，8500}和{(1200，0)，(600，0)，(600，300)，(0，300)，(0，600)}。列车停站时间、最小和最大发车间隔时间分别1，3，6 min；区间运行时间分别为{3，2，3，3，3，3，3，2，2，2，2，2}。由于本文假定乘客不存在二次等待的情况，乘客等待的最长时间均不会超过列车最大发车间隔。客运票价根据地铁实际收费标准按里程分段为3～5元，货运票价对应按里程取值为5～20元。为更进一步降低运营成本，目标函数权重系数与量纲乘积分别为{1，10}。本文利用Visual Studio2015 平台编写VB 代码调用CPLEX12.6.1 求解模型，并设置终止条件为上、下界Gap 达到5%或者计算时间达到3 h。值得说明的是，由于某些参数在实际运营中难以获取，本文数值实验所用数据，除线路数据和客流数据外，其它数据的取值均是结合实际规律根据经验给出的数值。特别的，实际中影响列车运营成本的因素众多，例如，列车类型、列车运营里程、列车检修等，由于本文未考虑大小交路运营组织模式，所有列车运营里程相同。因此，本文数值实验中列车运营成本取值与列车类型相关并考虑大编组节省费用因素。该取值方法虽然在一定程度上体现了运营成本与列车类型之间的关系，但相对较为粗糙，在今后研究中将进一步细化成本分析。北京地铁八通线客、货需求分布如图2所示。

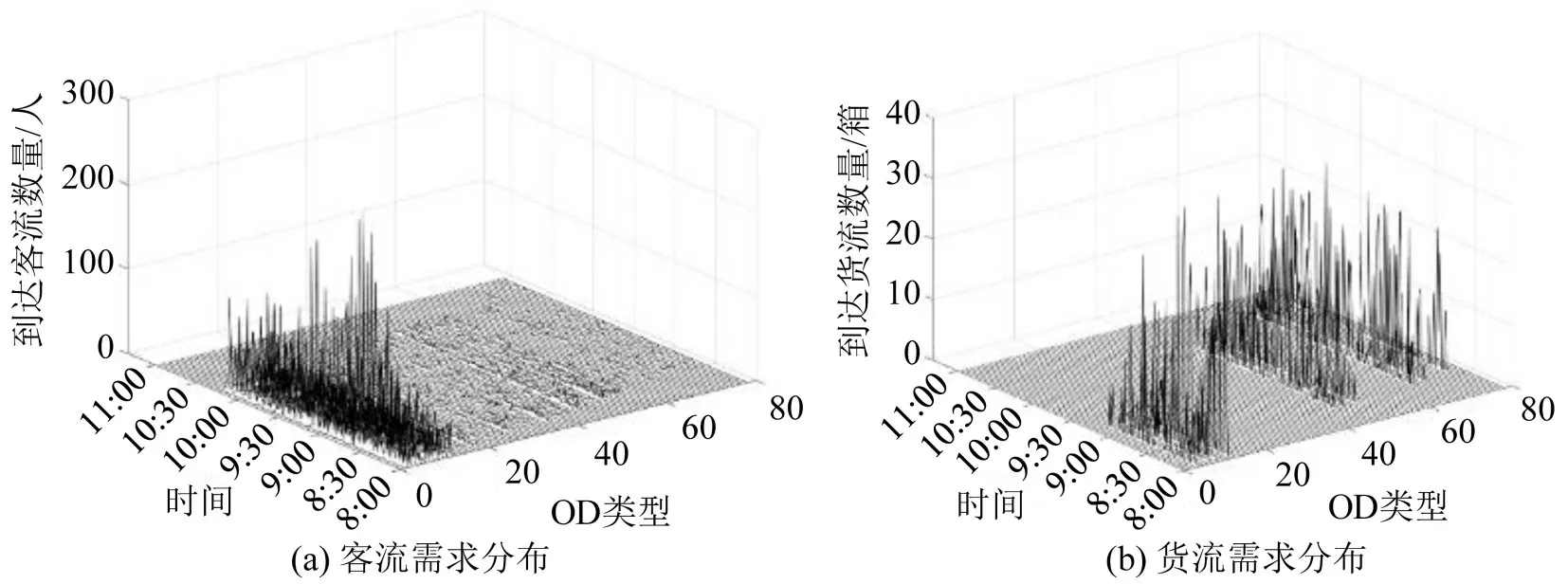
图2 北京地铁八通线客、货需求分布Fig.2 Diagram of passenger and freight demands for Beijing metro Batong line

由图2可知，客流存在明显的随时间变化的波动性和空间分布的不均衡性。同样的，考虑四惠、双桥、通州北苑、九棵树、土桥这5座可办理货运服务的车站，其货流需求亦存在随时间变化的波动性和空间分布的不均衡性。

3.2 结果分析

基于以上数据和参数设置，经过不到2 h(6326 s)的计算，在与最优目标值Gap 为0.00 时算法终止，得到最优方案，乘客等待时间为109722 min，总运营成本(运营成本减去客货运输收益)为140927 元。所得方案中，27列列车为大编组客运列车，7列列车为客货混合编组列车，1列列车为大编组货运列车。

所得方案列车运行图和编组方案如图3所示，图3中实心矩形代表货运车厢，未填充矩形为客运列车车厢。

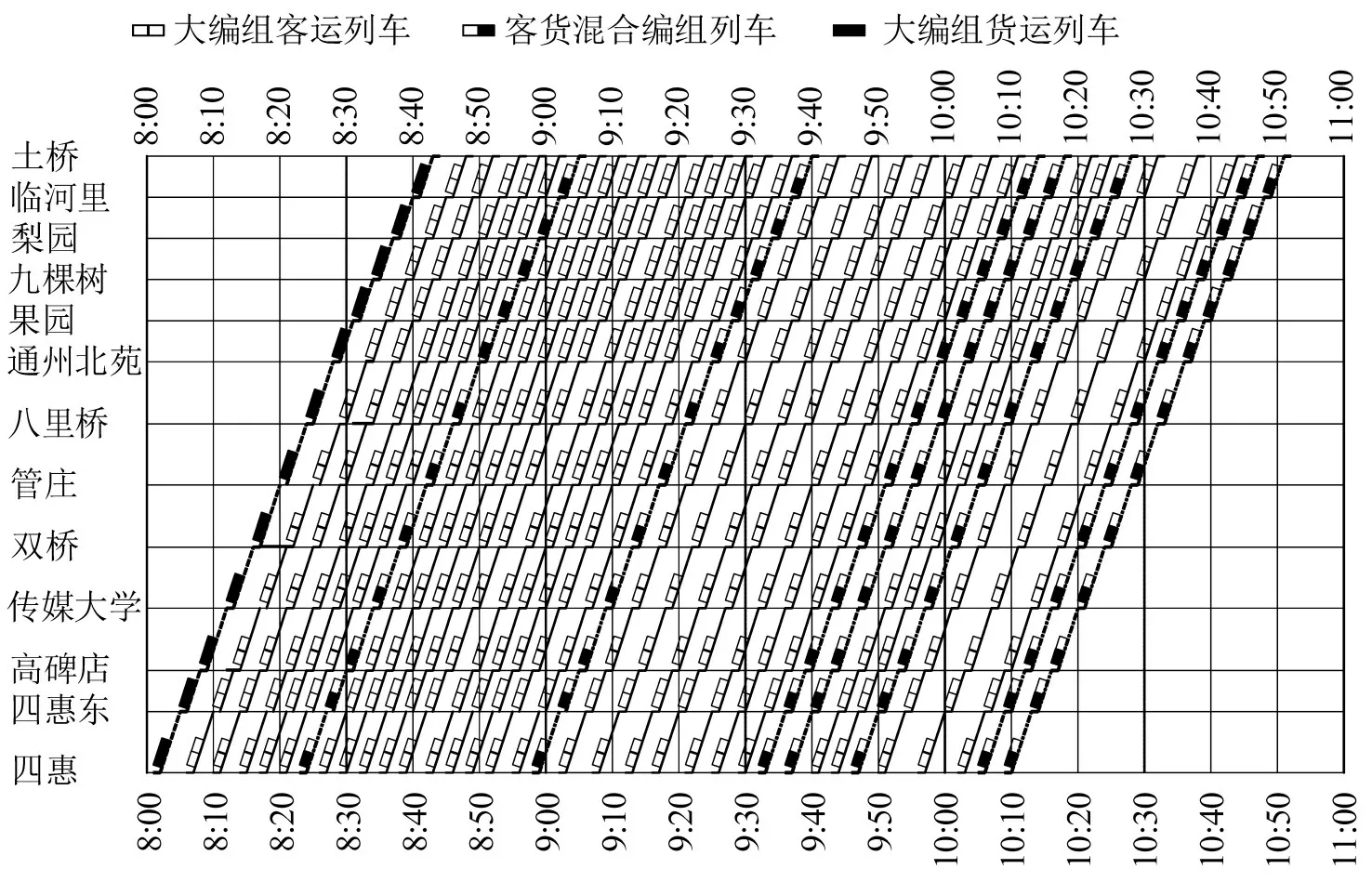
图3 本文模型所得北京地铁八通线列车运行Fig.3 Train working diagram for Beijing metro Batong line obtained by formulated model

由于本文所考虑客流量相对较大，大部分客运列车为大编组客运列车，只有少部分为客货混合编组列车以完成客货协同运输；同时，由图3可以看出，在客流需求较密集的情况下，多开行客运列车，客流需求较小时开行客货混合编组列车，且在开行大编组客运列车时列车间间隔相对较大以提高列车的载客率。此外，由于第1列列车离开车站时客流量较小，故第1 列列车可安排为货运列车，为货物运输提供服务。上述结果进一步说明了本文所提基于灵活编组的客货协同运输能更好地利用轨道交通运输资源，带来一定的经济效益。值得说明的是，客货运收益随着票价的变化产生一定的影响，但过高的运价会导致部分客货流的损失，综合考虑客货运票价与运营方案之间的平衡将在未来进一步研究。

由于本文所构建模型为具有一般性的数学优化模型，可通过给定部分决策变量的具体取值对模型进行拓展，以满足实际中的特殊需要。为进一步说明基于灵活编组的客货共运协同优化方法的有效性，本文分别针对灵活编组、固定编组下进行客货运输和固定编组模式下只进行客流运输分别求解所构建的数学模型。不同情形下所得结果如表2所示。

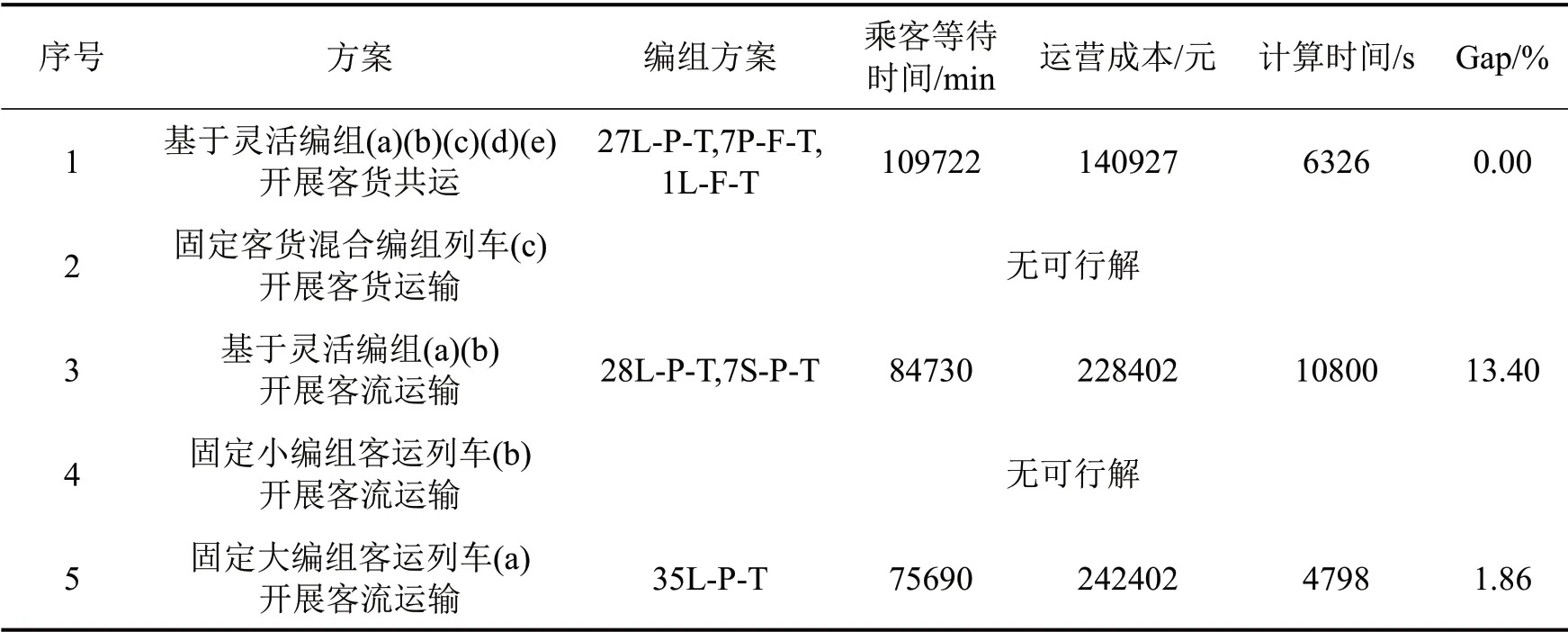
表2 各方案结果Table 2 Comparison of experimental results

灵活编组模式下进行乘客运输的列车运行图与编组方案如图4所示。

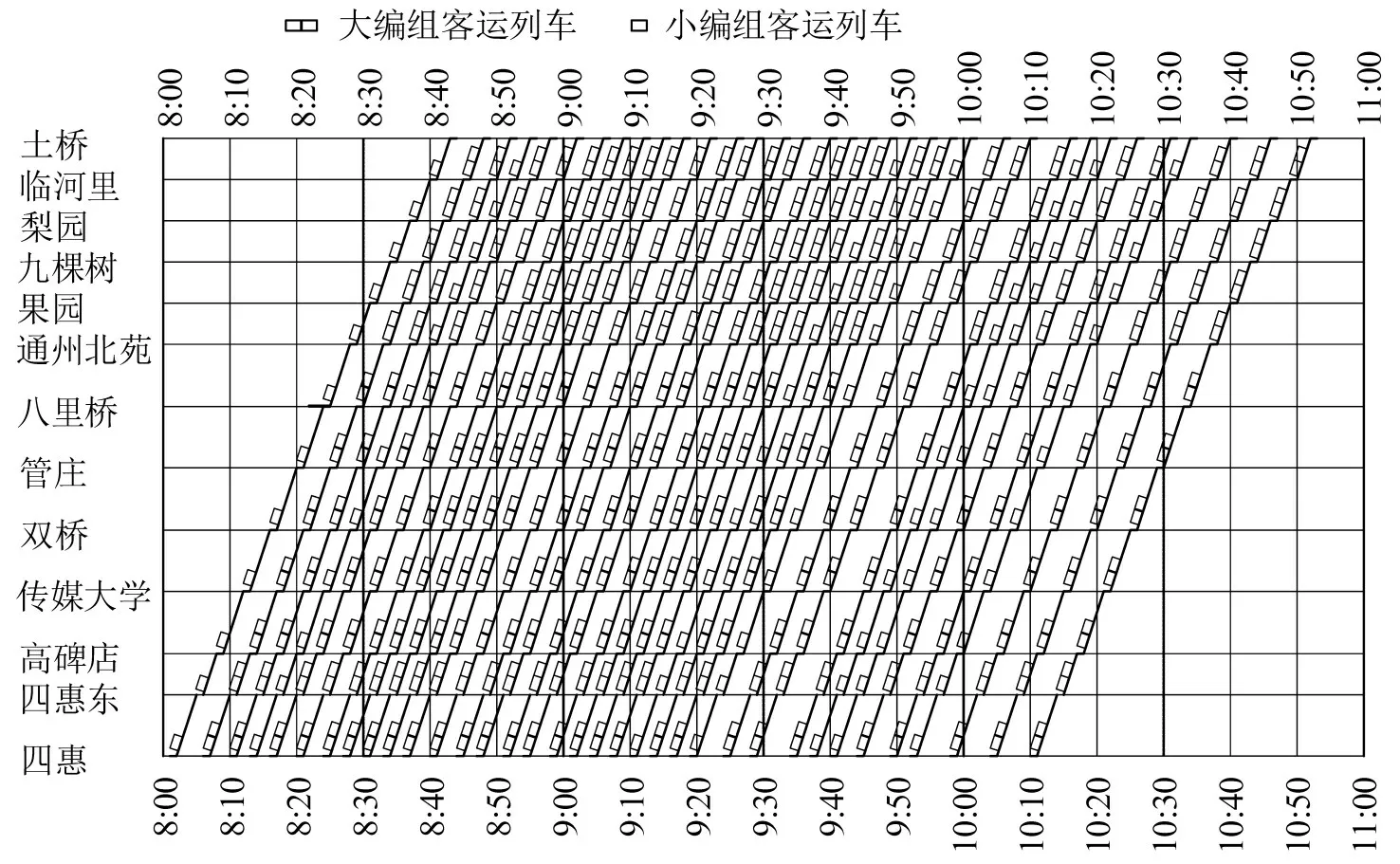
图4 只进行乘客运输所得北京地铁八通线列车运行Fig.4 Train working diagram for Beijing metro Batong line

由图3和图4以及表2可以看出，由于本文不允许乘客存在二次等待的情形发生，固定小编组和固定混合编组模式下无法得到可行解，需要开行一定数量的大编组客运列车，导致传统固定编组模式下所得方案需全部开行大编组客运列车以满足乘客运输服务要求，进一步说明了结合灵活编组运营组织模式开展客货协同运输的重要性。另外，相较于固定大编组客运列车开展乘客运输，灵活编组模式虽然会在一定程度上增加乘客等待时间(仅增加0.31 min 左右乘客平均等待时间)，但可降低约5.78%运营成本。同时，在客运的基础上，开展客货协同运输，可在确保必要的乘客运输服务质量的前提下(仅增加1.1 min 左右乘客平均等待时间且所有乘客均不存在二次等待情形)，降低约41.86%的运营成本，大幅度增加运营收益。特别是在相同运量的情况下，运输高价值货物时，开展货物运输带来的收益优势将更加明显。但值得注意的是高价值货物运输对服务质量具有更高的要求，对货源的稳定性具有更高的要求。因此，从经济学的角度，综合考虑不同价值货物运输及货源稳定性等因素以及更加精细化的运营成本分析，研究基于灵活编组的客货协同运输一体化优化将是进一步的研究方向。

4 结论

本文基于灵活编组运营组织模式，研究轨道交通客货协同运输方案优化问题，建立了以乘客等待时间和运营公司运营成本极小化为目标的数学优化模型，对列车编组方案、列车运行图和客货运输方案进行协同优化决策。案例分析表明：

(1)相较于固定的单一编组运营模式，灵活编组运营模式可更好地应对客流需求变化，降低运营公司运营费用。特别是相较于大编组运营模式，灵活编组模式可在仅增加0.31 min 左右乘客平均等待时间的情况下，降低约5.78%的运营成本。

(2)相较于单一的客流运输组织模式，在客流需求未饱和的条件下，结合灵活编组运营组织模式开展客货协同运输，可在乘客平均等待时间仅增加1.1 min 左右且所有乘客均不存在二次等待情形下，降低约41.86%的运营成本。

(3)基于灵活编组模式的轨道交通客货协同运输优化方法，虽然在一定的程度上增加了操作和模型求解难度，但可以较好地将灵活编组运输组织模式和客货协同运输的优点相结合，更好地实现列车运能与需求的良好匹配。值得注意的是，本文所构建模型是更具有一般性的数学优化模型，当给定编组类型集合且没有货流输入时，本文模型即可退化为传统的单一编组模式下客流运输优化模型。