方形微通道内超临界CO2流动换热特性研究

许婉婷，许波，王鑫，陈振乾

（东南大学能源与环境学院，江苏南京 210096）

引 言

在当前“双碳”目标的政策背景以及热工设备小型化的行业趋势下，超临界二氧化碳因其独特的物性优势在核反应堆、太阳能热发电系统、新型制冷与空调系统、火箭推动器的热保护等领域备受青睐，以超临界CO2为传热流体的微通道换热器将成为下一代高效能源系统的重要组成部分[1−4]。二氧化碳的临界点较低（Pc= 7.38 MPa，Tc= 304.13 K），其超临界状态较易获得，使用CO2作为换热工质的动力转换系统在较低的工作温度和压力下便可以获得较高的系统效率[5]。然而，如图1 所示，超临界CO2在拟临界温度附近，其热物性参数（密度、比热容、黏度和热导率等）变化剧烈，传统的常物性流动换热规律和经验公式不再适用。因此，全面了解超临界CO2在管内的流动换热特性对微通道换热器的设计和优化具有重要意义。

自20 世纪50 年代以来，国内外学者对超临界CO2的换热特性进行了大量的实验和数值模拟研究，但是主要针对竖直圆管内的向上和向下流动[6−9]。事实上，非竖直方向流动时，重力与流体流动方向并不平行，超临界CO2在管内流动时更易受到浮升力的影响，换热规律更加复杂。Liao 等[10]实验研究发现超临界CO2在水平微型圆管内流动时，在部分工况下会出现局部换热恶化，而在向上和向下流动时均在一定程度上强化了换热。Kim 等[11]进行了超临界CO2在内径为7.5 mm水平管内对流换热的实验研究，结果表明，由于浮升力的作用，壁温呈现出非均匀分布的特点。Wang 等[12]数值模拟了直径为22.14 mm的水平圆管内超临界CO2的流动换热特性，发现浮升力主要通过诱导二次流影响流动结构和湍流水平。Kumar 等[13]采用参数化模拟方法研究了超临界CO2在内径为2 mm 水平圆管内的热工性能，指出热通量对换热恶化有显著影响，较高的热通量会导致传热系数峰值的降低。关于热通量对传热系数的影响，也有学者提出了不同的见解。Xiang 等[14]对超临界CO2在冷却条件下的水平管内对流换热进行了数值研究，指出热通量对传热系数峰值数值影响不明显，但对峰值出现的位置影响较大。杨传勇等[15]模拟分析了超临界CO2在内径为0.5 mm、倾斜向上30°的圆管内的对流换热过程，结果表明上母线壁温高于下母线，相比于质量流量，热通量对上母线处的传热系数、相对二次流动能影响较小。闫晨帅等[16]对超临界CO2在内径为10 mm、倾斜角度为45°的加热圆管内的换热行为进行数值模拟，指出类气膜厚度、湍动能和轴向速度是造成顶母线壁温分布出现差异的主要因素。

上述研究绝大多数是在圆形直管中进行的，实际上，管型的不同往往会影响流体的流动换热特性。由于半圆形通道和方形通道在印刷电路板式换热器中表现出的结构紧凑、密闭性好、金属材料耗材少的特点，应用前景广阔，已有研究者对方管[17−18]、半圆管[19−21]中的超临界CO2换热特性进行了研究。此外，凹管[22]、螺旋管[23]、U 型管[24]等强化管道也引起了学者的极大兴趣。Kim 等[25]实验研究了圆形、三角形和正方形通道壁面温度的变化规律，对于非圆形通道，在相同的工况条件下，壁面温度峰值比圆形通道出现得早。Hasan 等[26]数值模拟分析了不同截面（方形、矩形、等三角形和梯形）通道形状对相同体积换热器性能的影响，结果表明，方形通道的综合性能优于其他三种通道。Besarati 等[27]建立了超临界CO2在方形通道内从530℃被加热到700℃时的传热模型和压降模型，通过数值计算得出结论，方形通道的水力直径越大，热性能越差，质量流率的增加有利于换热。Zhang 等[28]对超临界CO2在水力直径为1.16 mm 的圆管、半圆形管、方形管三种管型中的热力学特性进行了数值研究，结果表明用半圆管和方管代替圆管可以减弱加热条件下入口效应和浮升力效应造成的局部换热恶化现象。Lei 等[29]数值研究了水平方形波状微通道内超临界CO2的冷却换热行为，结果表明，在一定程度上增大振幅或者减小波长，有利于提高综合换热性能。Khalesi 等[30]对超临界CO2和液体钠在方形微通道内的层流和耦合传热进行了数值分析，在临界区和拟临界区，超临界CO2性质的剧烈变化会影响流动和传热，操作条件越远离临界点，这种影响就越小。

目前超临界CO2在大直径圆管内的流动换热研究较为广泛，关于非圆形微通道内流动换热行为的研究较少，尤其是倾斜角度对其的影响更少有涉及。本文在验证SSTk−ω湍流模型准确性的基础上，对比分析超临界CO2在方形微通道和半圆形微通道内水平流动的换热性能差异，以方形微通道为研究重点，通过对比三种壁面平均传热系数探究常重力条件下热通量、质量流量和倾斜角度对换热性能的影响，并从沿程浮升力参数和二次流强度的角度分析运行参数影响换热水平的原因，为后续方形微通道管内流动的强化换热奠定基础。

1 数值模型

1.1 物理模型与边界条件

方形微通道和半圆形微通道的物理模型如图2所示，管道截面的水力直径均为Dh= 0.9 mm，管道总长均为1000 mm。为避免入口端的入口效应及出口端的回流效应，在加热段两端各设置长度为200 mm 的绝热段，管道的有效加热长度为600 mm。建立物理模型时，z轴正方向始终为流体的流动方向，流体流动方向与水平面的夹角为α，定义α=0°为水平方向流动，α=90°为竖直向上流动，α=−90°为竖直向下流动。将方管类比圆管，沿流动方向的截面上周向角度为θ，从y轴正半轴顺时针旋转，定义其范围为θ∈[0°～360°]。

为研究超临界CO2在近临界点区域于方形微通道的流动换热特性，本文探讨了8.0 MPa 压力下，质量流量G、热通量q及倾斜角度α对流动换热特性的影响，边界条件设置如表1。

表1 不同模拟工况的边界条件设置Table 1 Boundary conditions under different simulated conditions

1.2 模型假设与计算方法

为简化模型，做出如下假设：

（1）流体在管内为稳态流动，无内热源；

（2）壁面热通量是均匀的；

（3）忽略流体流动时外壁与环境之间的热交换；

（4）忽略管道壁厚。

采用CFD 模拟软件数值求解连续性方程、能量方程、动量方程得到超临界CO2在管内的流动换热过程，其表达式分别如下：

式中，ρ为密度；μ为动力黏度；μt为湍流动力黏度；Pr为Prandtl数；Prt为湍流Prandtl数。

由于超临界CO2在拟临界温度附近热物性参数变化的剧烈性，选取合适的湍流模型以准确捕捉其在流动过程中各项物性的变化是数值模拟的难点之一。根据已有文献，数值模拟分析超临界CO2管内流动特性时，多数均选取低Reynolds数湍流模型，已有多位学者证实SSTk−ω模型在超临界流体流动换热模拟的优越性[9,14,20,31]。SSTk−ω模型融合了k−ε模型对充分发展主流区域湍流计算的鲁棒性和k−ω模型对近壁面区域流体流动特性的细致捕捉，能够有效地体现出浮升力效应的影响，其输运方程如下[32]：

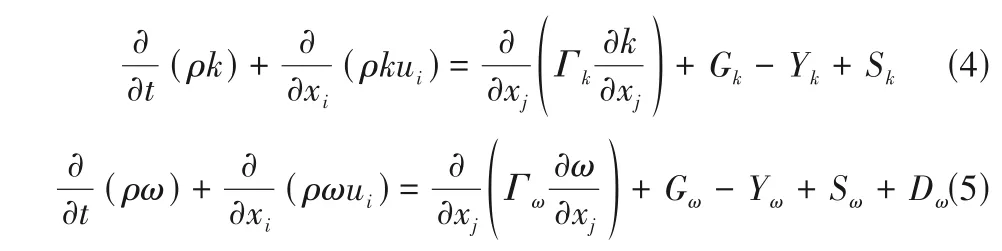
式中，Γk和Γω分别表示k和ω的有效扩散系数;Gk和Gω分别表示k和ω的产生项；Yk和Yω分别表示由于湍流产生的k和ω的耗散项；Sk和Sω分别表示k和ω的自定义源项；Dω表示交叉扩散项。

流体入口设置为质量流量入口，出口为压力出口边界，入口绝热段和出口绝热段设置为绝热壁面边界，有效加热段设置为恒热流壁面。采用有限体积法离散各项控制方程，压力−速度耦合方程采用SIMPLEC 算法求解，动量方程、能量方程等均采用二阶迎风格式，亚松弛因子保持默认值不变。计算时直接调用Fluent中的nist−real−gas−model 模型，以准确反映流动换热过程的物性变化。当各项残差值均小于10−6，且出口温度的监测值保持不变时，可认为计算收敛。

1.3 网格划分及独立性检验

流体流动全域采用结构性网格的划分方式，由于SSTk−ω湍流模型对近壁面处的网格质量要求较高，网格划分时，加密处理近壁面处的网格，合理设置第一层网格高度，保证无量纲壁面距离y+小于1。核算验证模拟结果，y+均小于1，表明采用该网格可捕捉到近壁面处的流体流动特性。

为均衡网格数量和模拟精度之间的矛盾性，两种模型分别选择6 种不同数量的网格进行独立性检验。边界条件设置为：压力P= 8.0 MPa，入口温度Tin= 303.15 K，质量流量G= 400 kg/(m2·s)，热通量q= 60 kW/m2，倾斜角度为0°。本文以方形微通道为例给出具体的分析，不同网格尺寸下加热段出口的主流温度和局部平均传热系数偏差如表2 所示。

表2 不同尺寸网格下的流体温度和平均传热系数偏差Table 2 Deviations of bulk temperature and average heat transfer coefficient under different grid sizes

由表2 可知，网格径向尺寸和横向尺寸均与计算结果的精度相关，但是6 种网格的模拟结果相差不大，以网格6为基准作对比，流体温度最大相对误差均小于0.10%，平均传热系数最大相对误差均小于3.69%。考虑到计算时间和计算精度的均衡性，选取网格5 开展后续的模拟，可满足计算精度的需求。同样地，采取相同的方法进行半圆形微通道的网格独立性检验，均能够保证选用的网格满足计算精度的需求。

1.4 求解方法与模型验证

为获取各项局部参数，沿流体流动方向建立多个截面，每个截面的主流温度Tb定义为

由于浮升力效应的影响，加热管周向壁面温度及对流传热系数均呈现出不均匀的特征。局部平均传热系数have、上壁面平均传热系数htop和下壁面平均传热系数hbottom分别定义为

其中，ρ为密度，kg/m3；u为速度，m/s；cp为比定压热容，J/(kg·K)；A为横截面面积，m2；q为热通量，kW/m2。

湍流模型验证时，将模拟所得的局部平均传热系数have与Liao 等[33]、Wang 等[34]根据实验数据提出的传热关联式进行对比。Liao 等、Wang 等提出的传热关联式均考虑了超临界CO2在微细管道内流动时浮升力效应的影响，根据其适用条件，本文两种管型湍流模型验证基于的边界条件均为：P= 8.0 MPa，Tin=305 K，G=1000 kg/(m2·s)，q=75 kW/m2，α=0°。由图3 可看出，两个换热关联式均能够很好地预测超临界CO2在方形微通道的换热特性，由于模拟时管道形态及边界条件与实际操作情况有偏差，在拟临界温度点附近误差较大，但是最大相对误差不超过±20%，属于可接受的偏差范围。采用相同的方法验证SSTk−ω湍流模型对半圆形微通道的适用性，最大相对误差不超过±15%，偏差范围合理。

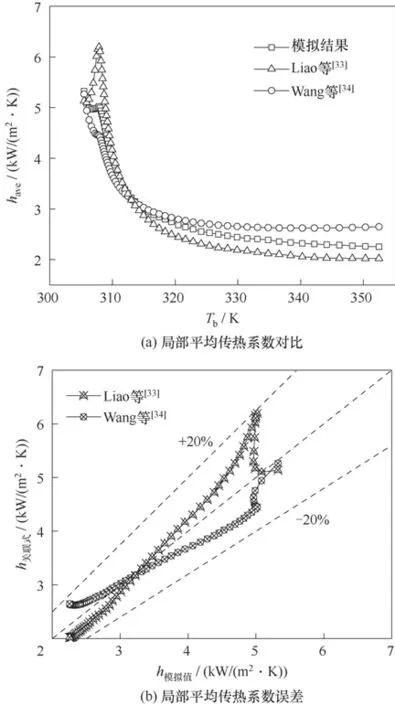
图3 模拟结果与传热关联式对比Fig.3 Comparisons of simulated results with predicted data from heat transfer correlations

2 结果与讨论

2.1 传热系数

2.1.1 管型的影响 本节模拟工况以P=8.0 MPa，Tin= 303.15 K，G= 400 kg/(m2·s)，q= 60 kW/m2，α=0°为例分析管型对超临界CO2流动换热的影响。本文将工质主流温度Tb＜Tpc的区域定义为类液区，将Tb＞Tpc的区域定义为类气区。

图4给出了常重力条件下方形微通道和半圆形微通道内沿流动方向局部平均传热系数have、上壁面平均传热系数htop、下壁面平均传热系数hbottom、主流温度Tb的变化情况。可以看出，两种管型中的三种传热系数和主流温度沿流动方向的变化呈类似的趋势。对比图4(a)、(b)可知，同等运行参数下，在同一位置，两种管型的流体温度基本一致；然而，方形微通道的have大于半圆形微通道的have，且在加热管的前半段，下壁面的传热增强程度比半圆形微通道内更大，此现象在拟临界温度附近尤为突出。在Lz= 500 ～800 mm 的管段，htop和hbottom之间的差值在方形微通道内逐渐缩小至零，而在半圆形微通道内始终存在，主要是由于半圆形微通道在重力方向上的结构不对称性造成的。水平方向流动时，方形微通道的整体换热效果优于半圆形微通道，故在下文的研究中，以方形微通道作为重点研究对象。

图4 方管和半圆管的壁面平均传热系数和流体温度（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s),q=60 kW/m2）Fig.4 Heat transfer coefficient and local bulk temperature in square and semicircular tubes

根据式（8）和式（9）关于htop和hbottom的定义，上、下壁面出现换热不均匀现象的直接原因是Tw,top和Tw,bottom之间存在差异。图5 给出了常、零重力两种条件下，方形微通道内Tb/Tpc= 1.0 截面周向壁面温度的分布情况。对比零重力条件下温度分布呈现出的对称性，可以看出常重力条件下超临界CO2在水平方形微通道内流动换热时，上、下换热不均匀现象主要是重力造成的。

图5 重力对壁面温度的影响(P=0.8 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s))Fig.5 Effect of gravity on wall temperature

下面将着重探讨常重力条件下热通量、质量流量和倾斜角度对传热系数的影响。根据图4(a)，在管道的后半段，即Lz= 500～800 mm 处，htop、hbottom与have之间的差别较小，故在下文分析运行参数对换热的影响时，仅展示Lz=200～500 mm管段的特性。

2.1.2 热通量和质量流量的影响 图6 和图7 分别给出了不同热通量和质量流量条件下，三种壁面平均传热系数随主流温度的变化曲线。由图6(a)和图7(a)可知，在类液区，随着热通量的增大或质量流量的减小，htop和hbottom均逐渐减小，且两者之间的差值逐渐增大，这意味着在主流温度相同的位置，外壁面施加的热量越高或单位时间内流过的流体越少，上壁面附近越容易聚集低密度的高温流体，上、下壁面之间的温差越大，换热不均匀性越强。拟临界温度附近，在低热通量（q=40 kW/m2）条件下，htop和hbottom变化趋势类似，均能够达到峰值，而在高热通量（q≥60 kW/m2）条件下，htop随主流温度的增大处于下降的趋势。在远离拟临界温度的管段，htop与hbottom之间的差异逐渐缩小并趋于一致。由图6(b)和图7(b)可以看出，随着热通量的减小或质量流量的增大，have逐渐增大，这与Kumar等[13]在水平圆管内得出的结论基本一致。

图6 热通量对传热系数的影响（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s)）Fig.6 Effect of heat flux on heat transfer coefficient

图7 质量流量对传热系数的影响（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2）Fig.7 Effect of mass flow rate on heat transfer coefficient

2.1.3 倾斜角度的影响 为研究倾斜角度对换热特性的影响，图8 给出了七种倾斜角度条件下（α=0°、30°、60°、90°、−30°、−60°、−90°）三种壁面平均传热系数的变化曲线。由图8(a)可以看出，除竖直流动（α= 90°和α= −90°）外，其他5 种倾斜角度条件下均呈现出上下换热不均匀的特点。当α= 0°时，htop与hbottom之间的差值最大，随着夹角α绝对值的增大，htop与hbottom之间的差值减小，且当竖直向上或向下流动时，两者之间的差值基本为零。根据图8(b)，have在竖直向下流动时最大，在竖直向上流动时最小，在水平流动时居中。整体表现为，一定压力条件下，在拟临界温度附近，夹角α的数值越小，局部平均传热系数越大，但是在远离拟临界温度的区域，倾斜角度对局部平均传热系数的影响较小。

图8 倾斜角度对传热系数的影响（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.8 Effect of inclination angle on heat transfer coefficient

2.2 浮升力效应

2.2.1 常重力条件下的基本特征 本节从浮升力效应的角度分析了常重力条件下微通道内超临界CO2的传热机理。同样地，以模拟工况P=8.0 MPa，Tin= 303.15 K，G= 400 kg/(m2·s)，q= 60 kW/m2，α=0°为例进行具体的分析。图9 给出了常重力条件下方形微通道内两个特征截面的温度分布云图和径向速度矢量图，在Tb/Tpc=1.0 截面，流体温度上下分布不均匀，且存在着明显的二次流现象，管道上半部分的流体温度高于下半部分，尤其是上壁面附近，大量的低密度高温流体在此处聚集，使得外壁面被施加的热量在向主流流体径向传递时热阻增加，降低了换热水平。在Tb/Tpc= 1.05 截面处，流体温度上下分布的不均匀性及二次流强度均减弱，这与图4(a)所示的htop与hbottom之间的差值随主流温度的增大而减小相对应。如图9 所示，方形微通道的四个尖角处，流体温度达到整个截面的峰值，在远离拟临界温度的管段，尖角处的径向速度也较小，低密度高温流体在此处更易聚集，不利于整体的热量传递。在实际工程应用中，考虑到换热效率及运行安全性，应最大程度地避免尖角的出现。

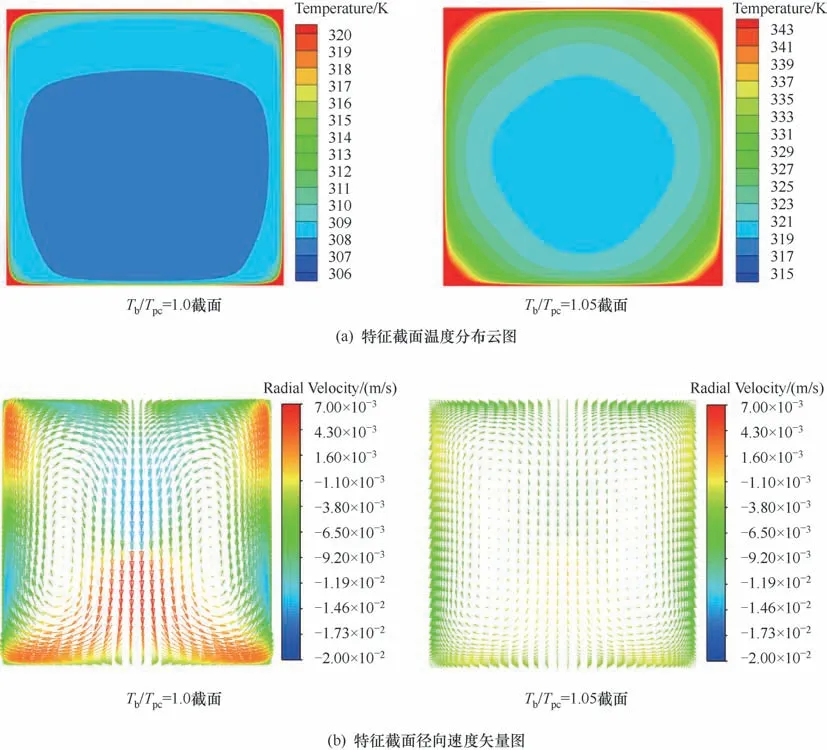
图9 特征截面处的典型参数分布Fig.9 Distribution of typical parameters at characteristic cross−sections

图10 给出了常重力条件下方形微通道内两个特征截面的轴向速度和湍动能径向分布曲线，受浮升力的影响，在拟临界温度附近，轴向速度的最大值及湍动能的最小值不再位于管道中心，而是在管道的下半部分，且上壁面附近的流体轴向速度和湍动能低于靠近下壁面的流体，这表明上壁面附近的流体并不能及时地将热量沿着流动方向向前传递。在远离拟临界温度的管段，截面上的轴向速度和湍动能的数值上下对称相等，浮升力的影响基本可以忽略。

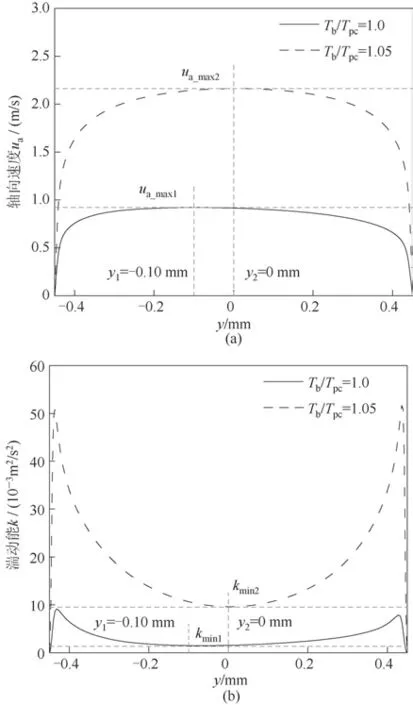
图10 特征截面处的轴向速度和湍动能径向分布曲线Fig.10 Radial distribution curves of axial velocity and turbulent kinetic energy at characteristic cross−sections

对于水平管道内的流动，浮升力参数Gr/Re2得到了广泛应用，很多学者[6,11,33]认为当Gr/Re2＞0.001时，浮升力的作用不能忽略，本文采用Gr/Re2定量表征流体流动过程中浮升力效应的影响。同时，为表征沿流动方向二次流强度的变化，引入二次流动能参数Ke，其表达式为[35−36]

式中，u和v分别表示方形微通道截面在x和y方向上的速度分量。图11 给出了方形微通道和半圆形微通道内Gr/Re2和Ke的沿程变化曲线，可以看出，在方形微通道的后半段，即Lz=400～800 mm 处，浮升力的影响基本可以忽略，且Tb/Tpc=1.05 截面恰好处于该范围。由图11(a)可以看出，两种管型在沿程同一位置的浮升力参数数值基本相同。根据图11(b)，二次流强度在类液区增加较快，在主流温度升至拟临界温度前达到峰值，在类气区随主流温度的增大逐渐减小并趋近于0。在类气区，同等运行参数下，在同一位置，半圆形微通道内的二次流强度高于方形微通道，这说明半圆形微通道在类气区换热效果较差是由于较强的二次流造成的。不难发现，二次流强度Ke比浮升力参数Gr/Re2在分析管型对传热的影响时更加适用。

图11 沿程浮升力参数和二次流强度变化曲线（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.11 Variation curves of buoyancy parameter and secondary flow intensity

2.2.2 热通量和质量流量的影响 热通量和质量流量对沿程浮升力参数及二次流强度的影响如图12和图13所示，随着热通量的增大或质量流量的减小，相同主流温度对应的截面上浮升力参数和二次流强度的数值逐渐增大，说明有更多的低密度流体沿管壁流至上壁面附近，这也是导致上、下壁面平均传热系数差值大的关键因素。在类液区，随着主流温度的增大，二次流强度显著增加，流体处于自然对流和强迫对流都存在的混合对流状态，浮升力效应不可忽略；在类气区，随着主流温度的升高，自然对流的作用逐渐减弱，二次流强度先急剧下降，再逐渐趋于平缓；当高于一定的主流温度时，浮升力效应基本可以忽略，且热通量越小或质量流量越大，越容易达到阈值。

图12 热通量对浮升力参数和二次流强度的影响（P=8.0 MPa,Tin=303.15 K,G=400 kg/(m2·s)）Fig.12 Effect of heat flux on buoyancy parameter and secondary flow intensity

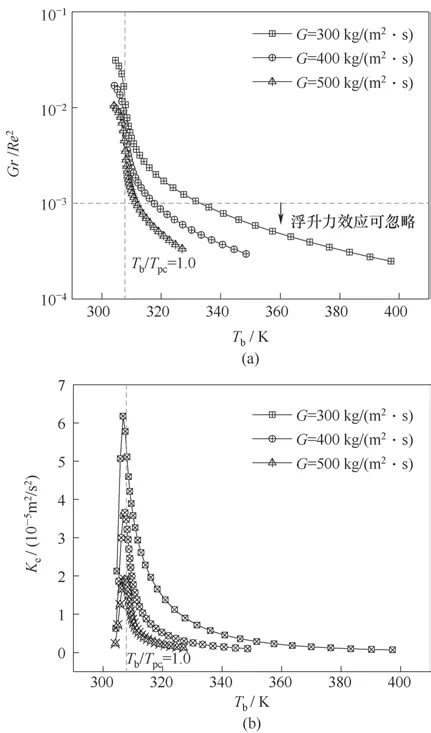
图13 质量流量对浮升力参数和二次流强度的影响（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2）Fig.13 Effect of mass flow rate on buoyancy parameter and secondary flow intensity

2.2.3 倾斜角度的影响 图14 给出了七种倾斜角度条件下沿程二次流强度的分布及Tb=Tpc截面的壁温分布曲线，可以看出，竖直方向流动时，由于浮升力方向和流体流动方向平行，二次流强度接近于零，且在Tb=Tpc截面，壁面温度的分布关于管道中心点中心对称。非竖直方向流动时，在拟临界温度附近，二次流强度的大小表现为：0° ＞30° ＞−30° ＞60°＞−60°，即倾斜角度越偏离水平方向，二次流强度越小，当夹角α的绝对值相等时，倾斜向下流动时的二次流强度明显小于倾斜向上流动时的工况。在远离拟临界温度的区域，二次流强度均较小，不同的是，在该区域，倾斜向上和倾斜向下之间的差异不再明显。在Tb=Tpc截面，上、下壁温的差值与二次流强度有关，二次流强度越大，上、下壁温的差值越大。相同主流温度所在的截面上二次流强度越大，说明在浮升力的作用下，高温低密度流体沿着壁面向上表面附近聚集的趋势越强烈，上、下壁面的温度差异越明显，尤其是在拟临界温度附近，上下换热的不均匀性越容易突显。

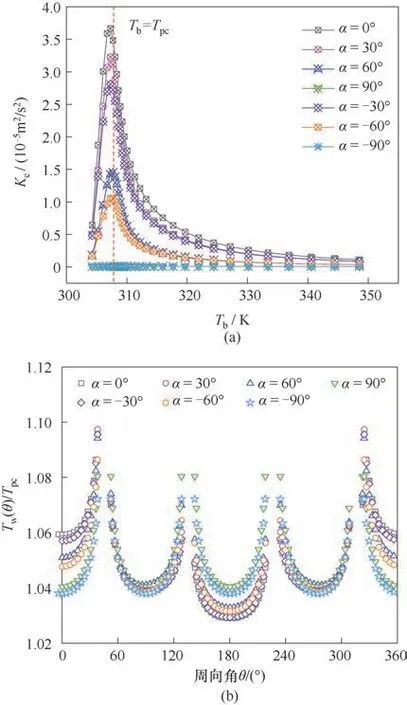
图14 倾斜角度对二次流强度和壁面温度的影响（P=8.0 MPa,Tin=303.15 K,q=60 kW/m2,G=400 kg/(m2·s)）Fig.14 Effect of inclination angle on secondary flow intensity and wall temperature

3 结 论

本文对微通道内超临界CO2的流动换热特性进行了数值模拟，在对比分析方形和半圆形微通道换热效果差异的基础上，进一步探讨热通量、质量流量和倾斜角度对方形微通道内换热特性的影响，得出主要结论如下。

（1）水平方向流动时，方形微通道整体换热效果优于相同水力直径的半圆形微通道。

（2）常重力条件下，非竖直方向流动时，重力方向上存在明显的换热不均匀现象，上壁面附近聚集更多低密度的高温工质，流体的轴向速度及湍动能处于较低水平，抑制了管壁热量的有效传递，沿程二次流强度的大小是其重要的影响因素，浮升力效应不可忽略。

（3）增大热通量、减小质量流量或减小夹角α的绝对值时，二次流强度显著增加，浮升力效应增强，htop与hbottom之间的差值增大。减小热通量、增大质量流量或减小夹角α的数值，有助于提升加热管的整体换热水平。

符 号 说 明

Gr——Grashof数

Lz——z轴方向上从原点到所在位置的长度，mm

Re——Reynolds数

下角标

ave——壁面平均值

b——主流体

bottom——下壁面

top——上壁面