阵列误差下的近场源PCA-BP参数估计算法

王 乐，赵佩瑶，王兰美，王桂宝

(1.西安电子科技大学 物理与光电工程学院，陕西 西安710071；2.西安电子科技大学 通信工程学院，陕西 西安710071；3.陕西理工大学 物理与电信工程学院，陕西 汉中 723001)

在无源定位、资源探测、声呐测向以及移动通信等众多领域，对于信号波达方向估计的探索一直都是热点[1]。到达角 (Direction of Arrival，DoA)估计技术最核心的应用就是智能天线技术，这一技术促进了现代通信的发展。虽然一些经典的高分辨率算法例如多重信号分类 (MUitiple SIgnal Classification，MUSIC)算法[2]、旋转不变技术估计信号参数 (Estimating Signal Parameter via Rotational Invariance Techniques，ESPRIT)算法[3]等可以准确无误地对信号来波方向进行估计，然而当有阵列误差存在时，该类算法的估计性能将会降低，因此必须对误差进行有效的校正。误差校正往往是根据不同的误差建立不同的误差模型，通过这些模型找到相应的方法来校正误差并进行到达角估计的。误差的建模是一个非常复杂的问题，如果同时存在多种误差，误差的建模将非常困难，相应的误差校正过程也非常繁琐，甚至有估计不准确等诸多问题。随着统计智能算法的飞速发展，有越来越多的统计智能算法被用于信号处理的到达角估计中，比如神经网络、支持向量回归算法等[4-10]。鉴于神经网络有良好的适应性能和非线性映射的特点，在建立预测信号模型的过程中，可以将空间中实际存在的噪声、阵列误差、传输通道等多种因素包含在训练过程中，因此不需要误差建模和误差校正，可以在进行参数估计时直接利用已经训练好的网络。目前方法在进行网络训练时，选取的信号特征为协方差矩阵的上三角元素，上三角元算得数目与阵元数目的平方成正比，因此对于大型阵列来说特征数目非常可观，这将导致网络模型非常复杂，网络训练时间加长。针对上述问题，笔者在进行近场源参数估计[11-12]时引入了主成分分析(Principal Component Analysis，PCA)方法[13-15]。该方法将降维后的特征用于神经网络的模型训练[16-18]，缩短了训练时间，降低了运算量，在存在阵列误差的情况下能对近场信号参数进行有效估计。

1 近场源阵列信号接收模型

当信号源位于天线阵列的近场区时，信号源的波前是球面波，因此不能采用和远场相同的方式来进行分析。笔者在接收近场信源时使用标量声压天线阵列，该模型中有M个全向阵元均匀排列，阵元间距为d，该阵列的结构图见图1，假设其中没有阵列误差。

图1 近场声源信号接收阵列结构图

假设有K个独立的近场非高斯信源入射到图1的阵列模型上，入射信号都是窄带信号，以坐标原点为参考阵元，rk表示第k个信源与参考阵元间的距离，θk表示第k个信源的入射角，快拍数值取P。在t时刻，第m个阵元中输出信号为

(1)

其中，1≤k≤K，1≤m≤M，sk(t)表示第k个入射信源，nm(t)表示第m个阵元接收的噪声矩阵。τmk表示第k个信源分别到达第m个阵元和参考阵元的时延差：

(2)

τmk≈mμk+m2ηk，

(3)

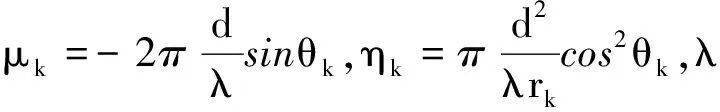
可得到第m个阵元上的接收信号：

(4)

第m个和-m个阵元的方差为

(5)

现有的子空间类方法大部分都是用这种方法对消掉距离因子，从而将距离和角度解耦合。然后进行两步参数估计。当存在阵列误差时，无法将第m个阵元和与其相对原点对称的第-m个阵元的距离因子相抵消，即式(5)不再成立，同时阵列导向矢量也因为误差的原因发生了变化，使得子空间类算法(如两步MUSIC算法)无效。

存在阵列误差时的阵列接收数据：

Xe(t)=AeS(t)+N(t) ，

(6)

其中，Ae=f(θ，r，er)是包含阵列误差的导向矢量矩阵，这个误差可以是位置误差、幅相误差、耦合误差，也可以是多种误差的组合，甚至很难给出误差的表达式，但这都不影响用笔者提出的方法进行正确的信号参数估计。因为笔者提出的方法将训练数据中包含的阵列误差和噪声、传输通道等多种因素包含在训练模型中，无须进行阵列误差建模校正，也不用进行谱峰搜索，对待估计信号参数进行预测时可以采用已经训练好的网络，可以实现低信噪比和存在阵列误差情况下的信号参数估计。

2 阵列PCA-BP算法

后向传播(Back Propagation，BP)神经网络[16-18]是多层前馈神经网络。该类网络根据误差逆向传播算法进行训练，广泛应用于函数逼近、模式识别、分类、数据压缩等方面。可以用图2简单表示其拓扑结构。

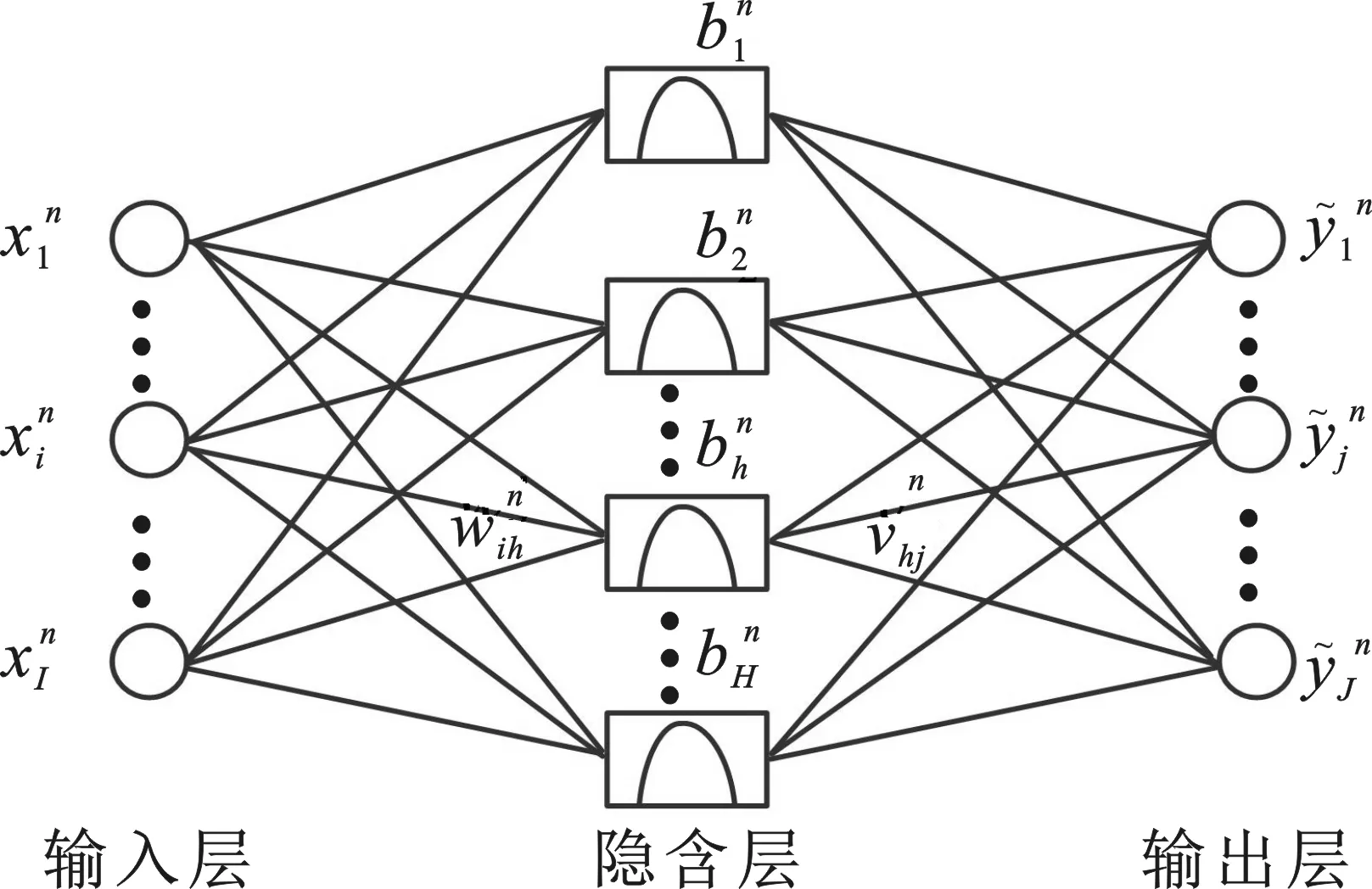
图2 BP神经网络拓扑结构示意图

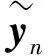
(7)

第j个输出层神经元的输出为

(8)

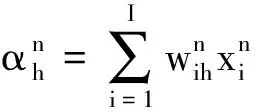
(9)

通过比较式(9)中得到的均方误差与设定达到的误差来决定是否更新权值和阈值。如果小于设定的误差，则完成迭代；如果仍大于设定的误差值，继续对权值和阈值进行更新，直到此值小于设定的误差要求值。

假设所选取的训练样本的数目为N个，阵元数为M，信源数为K，信号快拍数为P，使用的阵列PCA-BP算法对近场源参数估计的步骤如下：

① 根据式(6)分别计算出N个训练样本信号的协方差矩阵：

(10)

(11)

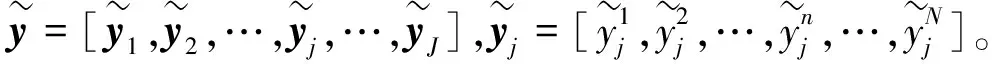
⑧ 对网络中的权值以及阈值进行更新。

⑨ 通过上面步骤，可以得到训练误差Ek，将该值与网络中设定的误差ek的大小作比较。若训练误差比设定误差小，则停止迭代，训练完成；否则返回步骤⑤ 。

⑩ 训练完成后从数据集中任选一组样本进行预测。

3 仿真实验

仿真实验两个近场、窄带、非高斯平稳声源信号入射到图1所示的均匀线性天线阵列上，该接收阵列有8个阵元，阵元间隔d=λ/4，信号频率设为[fs/8，fs/10]，fs是信号的采样频率，λ是频率为fs/8信号对应的波长，快拍数为200，噪声为高斯白噪声。训练样本数据的角度间隔Δθ=6°，距离间隔Δr=0.05λ，训练角度的区间设在[-90°，90°]，训练距离的区间设在[4λ，5λ]，笔者取主成分累积贡献率为95%。取173组样本数据，通过交叉取样将其分为两部分，分别用于训练和测试。取两个没有经过训练的信号进行预测，这两个信号的角度和距离参数为[10°，4.5λ，16°，4.55λ]，信噪比为10 dB，仿真结果如图3～图5所示。

图3表示各主成分的贡献率，可以看出前几个主成分的贡献率较高，从前往后依次衰减直到为0。文中主成分累积贡献率取值不小于95%；为满足这一条件需将前4个主成分作为后向传播神经网络的训练输入信号特征来训练网络。图4为文中算法训练所用的时间与BP算法、GRNN算法的比较图。笔者通过比较算法的训练时间研究了算法复杂度，为了避免偶然性，进行了10次仿真实验，取这10次训练时间的平均值，在数据量等同的情况下与其他算法进行了比较。由图4可知，文中算法、BP算法和GRNN算法的训练时间分别为3.340 5 s、 15.899 6 s和7.520 6 s。从这些数据上可知文中算法用的训练时间最少，即文中算法的时间复杂度是最低的，运算量也是最低的。文中算法进行预测耗费0.093 9 s，而两步MUSIC算法耗费1.348 5 s进行谱峰搜索，由此可得文中算法的预测时间远小于两步MUSIC算法所需的预测时间。

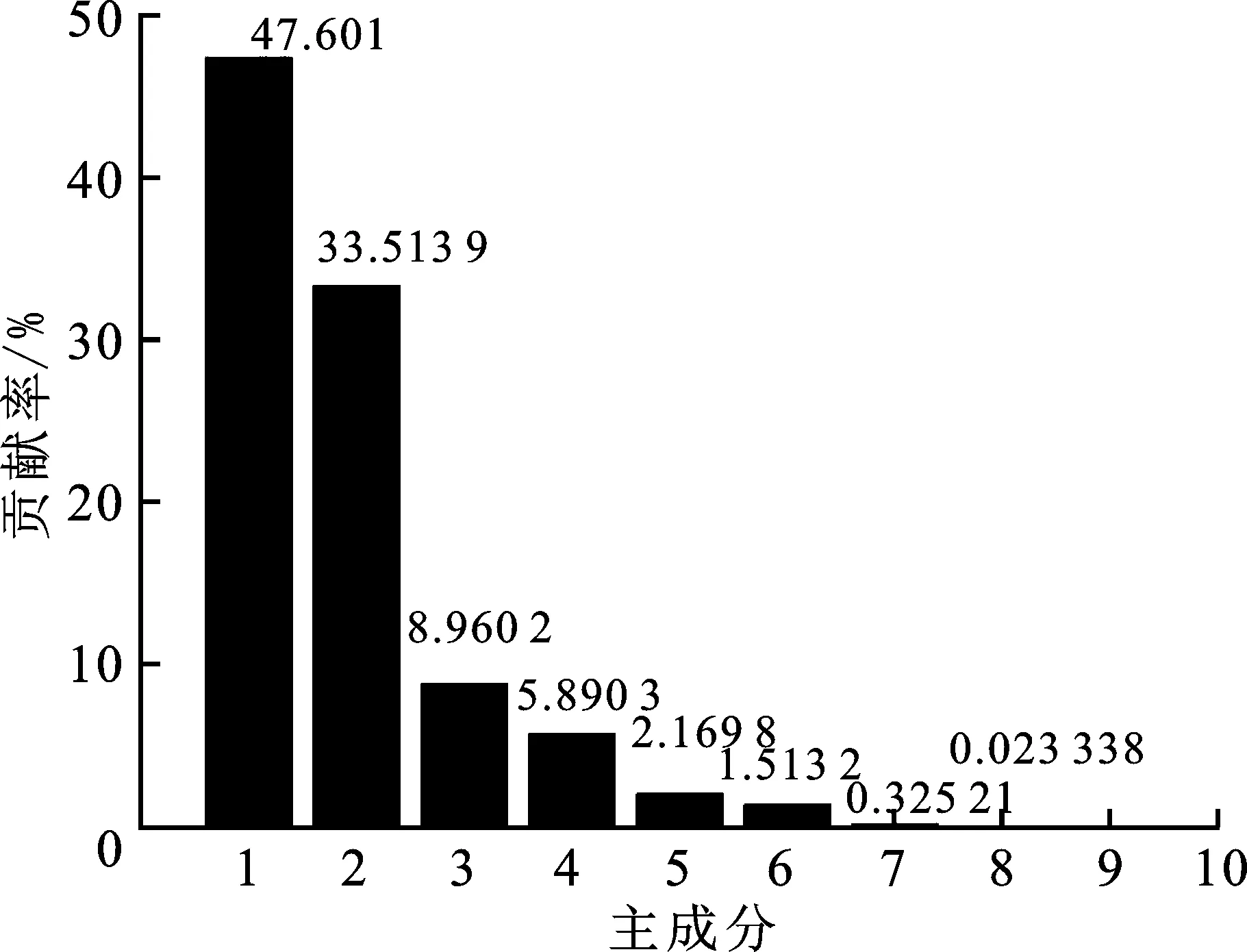
图3 阵列PCA-BP算法各主成分贡献率

图4 3种算法训练时间图

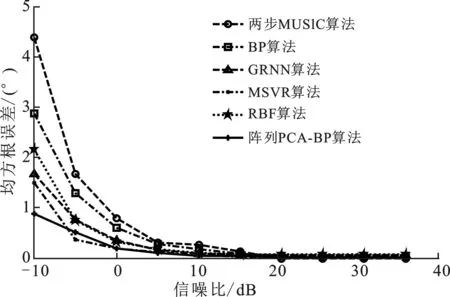
图5 均方根误差比较图

图5为文中阵列PCA-BP算法与两步MUSIC算法、BP算法、GRNN算法、MSVR算法的角度均方根误差比较图。由图可知当信噪比取值范围为-10 dB～20 dB时，文中算法的估计均方根误差值最小，性能优于其余4种算法，当取值高于20 dB时，进行仿真的5种算法的估计精度都比较好。

将仿真实验1中的阵列添加误差，其中添加的阵列误差包括幅相误差ee=diag[1.025，0.925，0.921，1.079，1.015，0.992，1.087，0.910，0.997，0.980，1.080]和阵列误差de=[0.27，0.28，0.29，0.30，0.24，0.23，0.21]λ，其他仿真条件不变。仿真结果如图6～图9所示。实验条件为P2.6 GHz GPU；4 GB内存；MATLAB2016b开发平台。

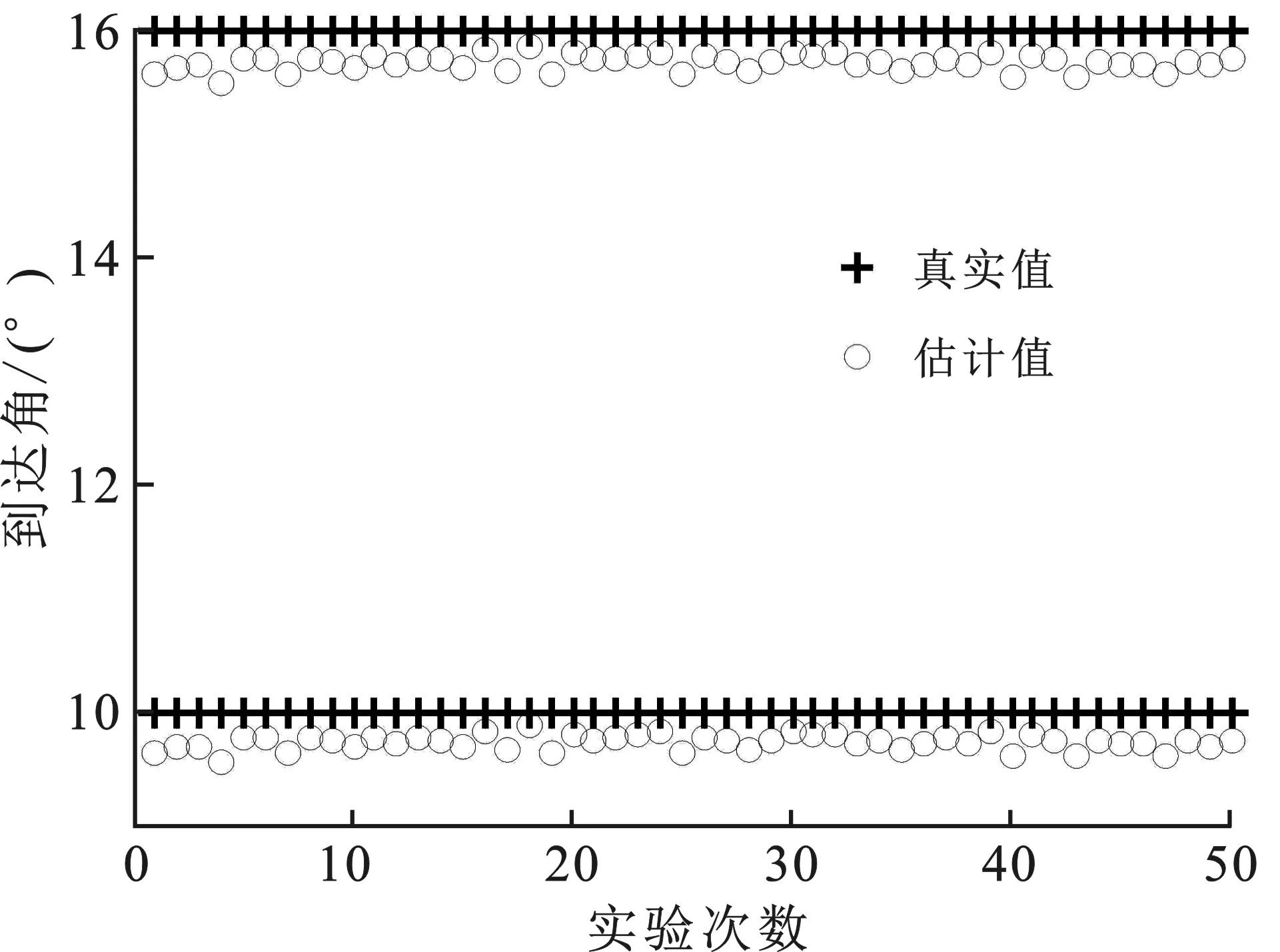
图6 存在阵列误差的阵列PCA-BP算法的角度散点图

图7 存在阵列误差的阵列PCA-BP算法的距离散点图

图6为在存在阵列误差的情况下使用文中阵列PCA-BP算法在10 dB信噪比下对两个未经训练的近场观测信号估计出的角度散点图。可以看出，估计得到的角度值和真实角度值相对应，两个信号的角度估计误差都在0.5°以内，真实值和估计值十分接近。图7为两个观测信号对应距离参数估计值的散点图。可以看出，估计得到的距离值和真实的距离值相吻合，误差都在0.005以内。因此，文中算法可以对近场源的角度和距离等参数进行有效的估计。

图8为当信噪比为10 dB时，两步MUSIC算法得到的观测信号估计角度散点图。从图中可以看出，估计出的角度参数和真实值完全不对应，第1个入射角的真实值和估计值误差接近10°，第2个入射角的真实值和估计值误差接近4°。图9为两步MUSIC算法估计得到的观测信号的距离参考阵元的距离的散点图。从图中可以看出，估计出的距离参数和真实值也是完全不对应的，真实距离和估计距离的误差都大于1。因此可以看出，在阵列误差存在的情况下，两步MUSIC算法对于近场源参数的估计是完全失效的，但文中算法的近场源参数估计结果依然比较准确。

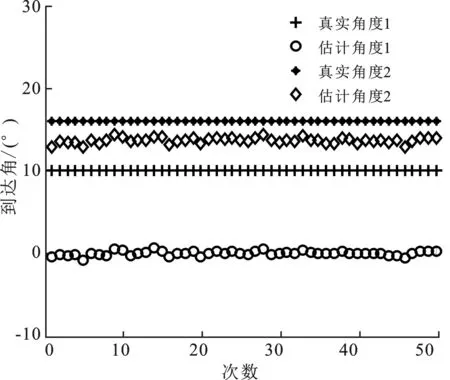
图8 存在阵列误差的阵列两步MUSIC算法的角度散点图

图9 存在阵列误差的两步MUSIC算法的距离散点图

4 结束语

笔者所提出PCA-BP近场源参数估计算法，能够在存在阵列误差的情况下完成信号参数的高精度估计。通过使用PCA算法降低输入神经网络的信号特征维数，可以减少BP网络中输入层神经元个数进而缩短训练时间，并且具有很好的抗噪能力。由仿真结果可知，文中算法优于传统的两步MUSIC算法、BP算法、GRNN算法以及MSVR算法。同时也表明了文中算法也能够在存在阵列误差的情况下，对于近场源的角度和距离参数进行准确的估计，避免误差建模和估计的繁琐过程，具有重要的理论意义和实用价值。