柔性变弯度后缘机翼的风洞试验模型优化设计

张桢锴，贾思嘉，宋晨,2,*，杨超

1. 北京航空航天大学 航空科学与工程学院，北京 100083 2. 北京航空航天大学 无人系统研究院，北京 100083

变弯度飞行器是一种能够改变机翼弯度的飞行器，在飞行过程中通过动态变弯度，使飞行器始终保持优良的气动与飞行性能，以提高飞行效率，减少碳排放。

为了实现机翼的变弯度能力，国内外提出了基于机械结构和基于智能材料结构的2种变形实现方式。不过，机械结构的方式往往会增加额外重量。相对而言，基于智能材料与结构的柔性机构方案具有更大的应用潜力。而这种方案要求变体飞行器的设计需要考虑多学科的结构、气动、控制分析方法，并定制特定设计工具。

通过载荷路径法设计柔顺机构实现变弯度后缘是目前的主流方案，该设计方法要求结构能够在特定的工况下达到某种目标变形。葛文杰等利用基于变密度法的柔性机构拓扑设计方法，采用玻璃纤维层合板设计了变弯度前缘和后缘，并针对变弯度后缘的几何大变形特性，采用了超弹性材料与非线性分析方法实现柔性前后缘方案。文献中直接给定了目标外形，并没有指出该目标外形是如何得到的。De Gaspari 和 Ricci建立了用于设计基于柔性机构变弯度机翼的双层优化方法，分层设计气动外形与内部结构机构，所设计的外形既能够满足气动要求，也能够满足最小驱动能量要求，并采用遗传算法和载荷路径法获得结构拓扑。基于该方法设计的风洞模型验证了设计工具的有效性，但由于模型的刚度较大，没有获得期望的机翼静气动弹性耦合特性。在此基础上，使用参数和形状优化技术改进了变弯度前缘，能够实现较高的变形形状精度。对比研究表明，在合适的求解器参数设置下，载荷路径法能够获得较为清晰的内部结构，更有利于后期的物理实现，因此在具体设计中，可以综合采用2种方法。复合材料层合板也被应用于变弯度机翼的蒙皮中，中国飞机强度研究所以变弯度前缘为例，对比研究了2种铺设优化方式的区别。南京航空航天大学王宇等，提出了变体机翼后缘机构多学科设计与优化方法，该优化框架中综合考虑了气动、材料和结构等多个学科，能够快速有效地实现设计目标。

目前，文献中均采用了结构标记点与目标外形上的目标点之间的最小平方误差(LSE)来衡量变弯度前后缘的变形精度。而不同的外形相似性判断标准下优化结果会有区别，缺乏不同曲线相似性准则的对比。并且，变弯度后缘的设计是一个需要综合考虑气动、结构和驱动的多学科优化设计，而现有的研究更加注重具有变形能力的结构的设计与实现工作，并没有系统地考虑多学科之间关系。

针对以上存在的问题，本文提出了考虑变弯度外形设计、结构参数优化和驱动器匹配的变弯度机翼设计优化框架，对比研究了LSE距离和Fréchet距离在变弯度后缘精确变形设计中的特点。并采用该框架，为变弯度后缘的风洞试验模型提供优选参数。

1 设计对象描述

设计对象为大展弦比双尾撑布局飞机，如图1 所示，全机翼展5.02 m，长2.5 m，总重量为26.0 kg，质心位于机头后1.07 m处，该位置也是机翼主梁与机身连接位置。该机翼采用低速厚翼型，最大相对厚度约为17%，位于40%弦长处。

图2展示了金属主梁与气动维形组成的弹性机翼结构。包括气动维形在内，单个机翼的展长为2.32 m，翼根弦长0.3 m，翼稍弦长0.12 m，平均气动弦长为0.216 8 m，展弦比为25.15，属于大展弦比飞行器。采用高强度7075号铝合金加工制造的金属主梁为主承力部件，重量约为2.56 kg。控制面位于展向16%～85%，弦长后40%区域。本文中，将对后缘控制面区域进行改造，安装上柔性变弯度后缘装置。

图1 参考飞机模型Fig.1 Reference aircraft model

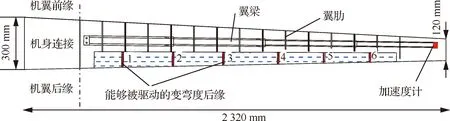
图2 大展弦比变弯度后缘机翼布局Fig.2 High-aspect-ratio wing equipped with compliant morphing trailing edge

2 优化设计方法

变弯度机翼的风洞试验模型设计流程按照先后顺序主要包括：气动外形设计、单个翼肋的柔性翼肋结构设计、机翼变弯度后缘的组合体设计、详细设计与试验，整个流程如图3所示。

首先，外形参数化模块根据需求定义机翼的目标外形；接着，针对其中的每一个展向站位的翼型，通过结构拓扑优化与后缘柔性翼肋结构参数优化的方式获得驱动肋的大致结构，并与机翼结构组合在一起形成变弯度机翼；最后，详细设计风洞试验模型，通过增材制造的方式实现，并进行风洞试验，以验证其承载能力、变形能力与精度，并测试气动收益。

变弯度后缘机翼的核心部件是变弯度后缘主动控制肋，也是本文的主要设计对象。该部件需要满足如下需求：① 变弯度后缘能够承受法向气动力且能维持光滑气动外形；② 变弯度后缘能够在有限驱动力下实现连续弯曲变形。

本文在先前研究的基础上，基于一系列给定的目标外形和拓扑结构，着重研究图3中的后缘肋结构参数优化设计部分。

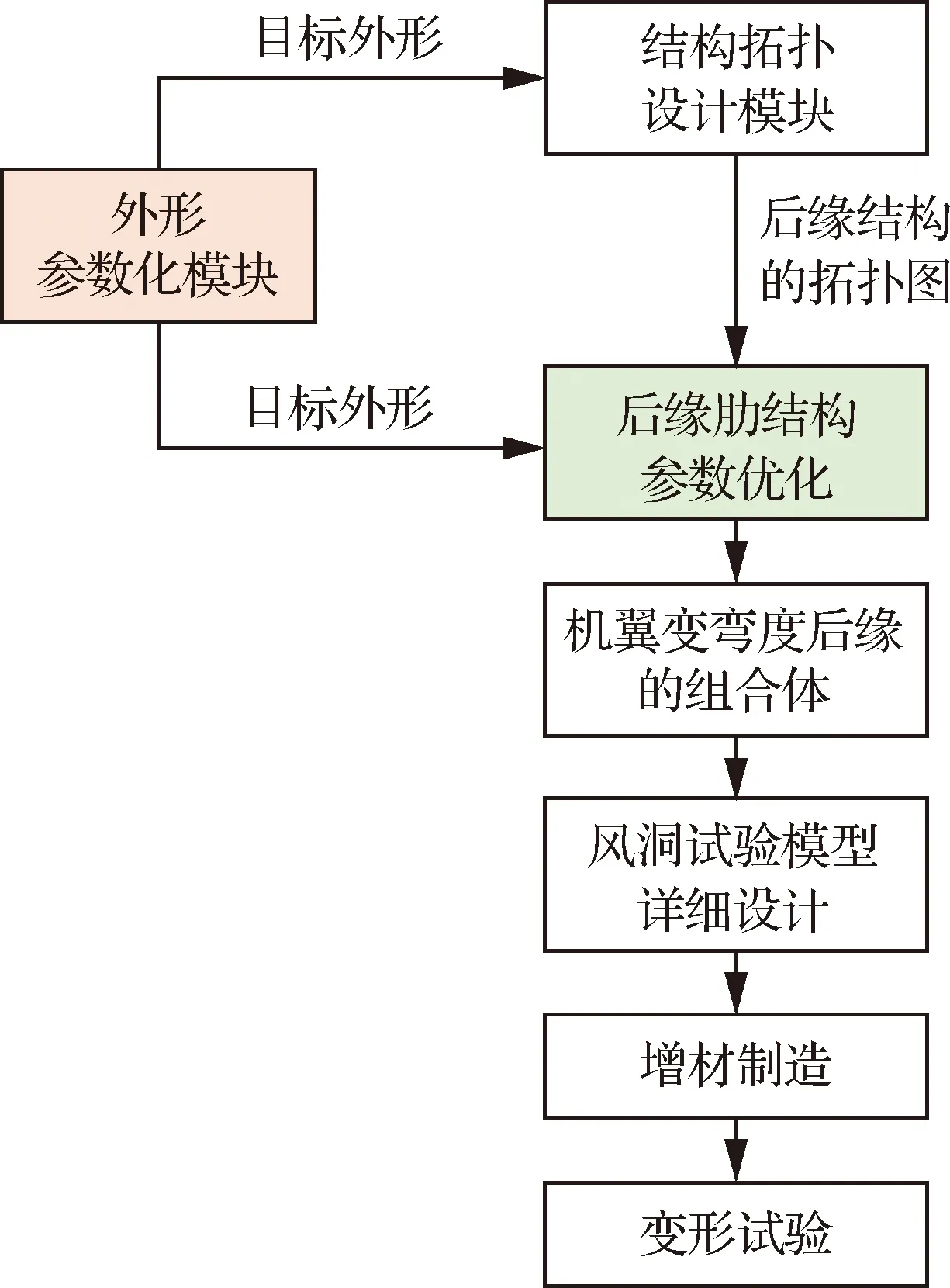
图3 变弯度机翼风洞试验模型设计流程Fig.3 Design process for wind tunnel model of wing equipped with compliant morphing trailing edge

2.1 参数化目标外形

本文使用外形参数化模块构建参数化基础外形和参数化变弯度外形，如图4所示。该模块的输入是常规飞机对象的机翼几何模型，根据机翼不同展向站位的剖面，构建出基于类/形状变换(CST)方法的参数化基础外形。

不同的变弯度飞机需求下，最优的变弯度外形不同。因此，根据气动、变形和蒙皮的需求，采用优化的方式得到参数化的变弯度外形，作为结构设计的目标外形。图5展示了基于机翼的CAD模型构建参数化机翼，并对参数化机翼进行变弯度控制，生成参数化变弯度机翼的过程。该变弯度外形的后缘位于60%弦长后，要求在后缘下偏15°后，通过设计变弯度后缘外形提高升力系数。在本文结构设计中，将选取参数化变弯度机翼的靠近翼根处的典型截面作为设计对象。

图4 变弯度后缘机翼的外形参数化模块Fig.4 Shape parameterization tool for morphing airfoil

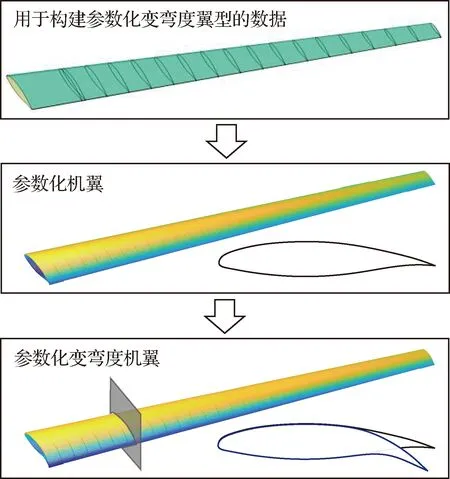
图5 从CAD模型建立参数化机翼，并建立参数化变弯度机翼Fig.5 Procedure for generating parametrized morphing wing from CAD model

本文采用的是基于柔性机构的变弯度后缘装置，采用蒙皮与内部结构整体设计方案，后缘的上表面主要是弯曲变形，不发生延展，下表面的蒙皮通过一个滑动铰链机构滑入机翼内部。因此，在设计目标外形时，设置了蒙皮上表面的弧长不变的约束。设计过程考虑了蒙皮的结构响应，以减小驱动变形所需要的力。表1总结了在气动外形优化中考虑的具体需求。

表1 外形优化中考虑的气动、变形和蒙皮需求

2.2 外形相似性准则

变弯度后缘在驱动力的作用下实现变形，而在进行结构参数优化设计时，设计目标之一是要求所发生的变形是尽可能地接近所给定的目标外形，其本质上是对具有空间位置的曲线相似性的度量。本文研究点与点之间的LSE距离和基于空间路径相似度描述方式的Fréchet距离在进行变弯度后缘精确变形优化设计中的区别。相较于传统的标记点与目标点之间的LSE距离，Fréchet距离进一步考虑了空间之间的距离关系，使得能够分析具有空间序列顺序曲线的相似性。这里，假设以和是二维平面R上的2条采用离散点序列描述的曲线:

式中：是位于曲线上的点，是位于曲线上的点，均按顺序排列。当点的数目=时，LSE距离、Fréchet距离如表2所示。LSE距离描述的平均距离，而Fréchet距离描述的是2条曲线之间最短的最大距离。

为了能够展示LSE距离与Fréchet距离之间的差别，采用sin函数生成了基准曲线和扰动曲线，如图6所示。基准曲线的形式为=sin，扰动曲线1为原有基准曲线的基础上增加了幅值为0.1的高斯噪声，扰动曲线2在其中一个采样点上，额外增加了幅值0.1的偏差。LSE距离的计算采用了2范数，离散Fréchet距离采用耦合点的方式，2种扰动曲线与基准曲线的距离如表3所示。扰动曲线1与基准曲线之间，LSE距离和Fréchet距离分别为0.024 2和0.049 9，两者相差不大。但是对其中一个数据点加入幅值为0.1的偏差后，LSE距离和Fréchet距离分别改变了27.6%和197.2%。相对于LSE距离，Fréchet距离对点的偏移更加敏感。这种特性使得Fréchet距离能够更加敏锐地捕捉到2条曲线上采样点的微小扰动。

表2 描述曲线相似性的距离计算公式Table 2 Distance for describing curve similarity

本文通过在后缘上确定标记点，并在目标变形上找到目标点的方式描述2条曲线之间的相似性。考虑到后缘发生变弯度后，翼型的弦长会发生改变，需要使用变形的物理特性寻找标记点与目标点之间的关系。本文所设计的变弯度后缘的上表面主要是弯曲变形，不发生明显的轴向伸缩，可以假设上表面弧长不变；而下表面的蒙皮通过一个滑动铰链机构滑入机翼内部，主要也是弯曲变形，不发生明显轴向变形。基于蒙皮弯曲变形假设，标记点占弧长的百分比位置在变弯度前后不变，由此可以找到变弯度变形后的目标点，如图7 所示，详细的标记点与目标点位置参见附录表A1，坐标系原点位于前缘。

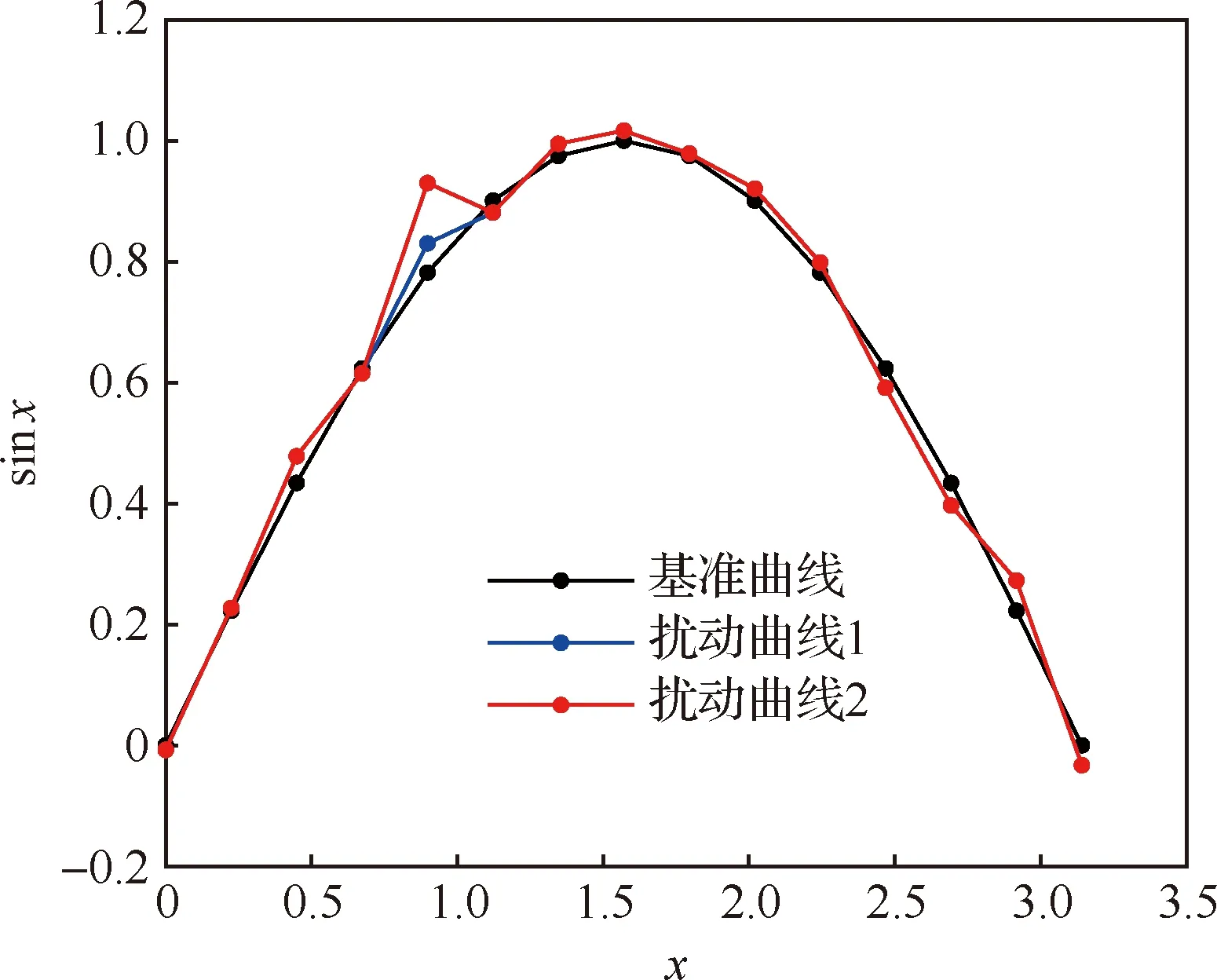
图6 使用sin函数表示的基准曲线，以及扰动曲线1和扰动曲线2Fig.6 Reference curve generated by sin function, disturbance Curve 1, and disturbance Curve 2

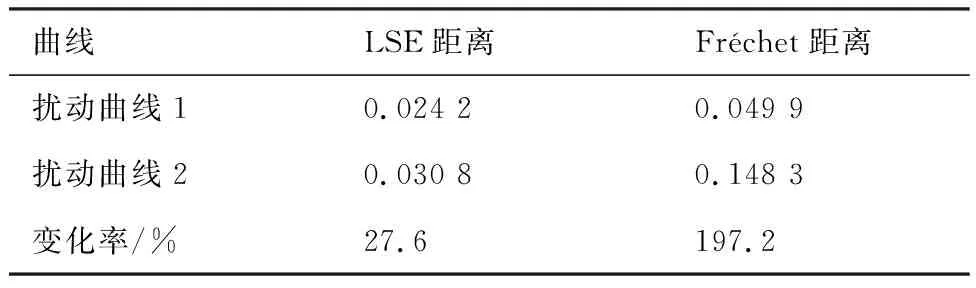
表3 曲线之间的LSE距离和Fréchet距离

图7 变弯度后缘的标记点与目标点Fig.7 Marker points and target points of morphing trailing edge

2.3 设计区域边界条件

在风洞试验中，变弯度后缘会受到外部气动力与驱动力的联合作用，需要确定边界条件。本文采用高阶面元法，作用在三维机翼上的气动力进行了分析。典型的风洞试验状态为来流速度30 m/s, 迎角为5°。基础外形的升力系数为0.515 0，而变弯度构型的升力系数为1.123 0。图8对比了在基础外形与变弯度外形的展向升力分布，横坐标采用了无量纲展长，纵坐标为使用平

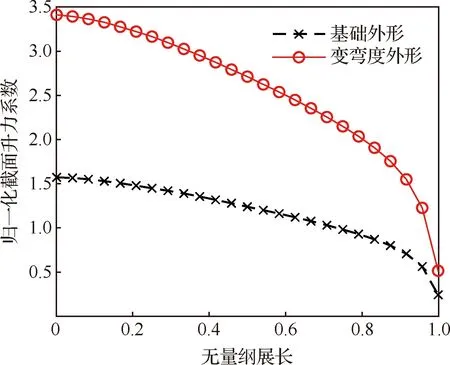
图8 在迎角为5°，使用面元法计算得到的机翼展向升力分布Fig.8 Spanwise lift distribution, calculated using panel method, at angle of attack of 5 degrees

均气动弦长归一化的截面升力系数。由于弯度增加，总升力显著增加。

图9对比了10%展向站位处机翼上下表面的压力系数分布，横坐标为有量纲弦长。由于后缘变弯度过程中上表面蒙皮的弧长保持不变，使得变弯度后缘的弦长略小于基础外形。变弯度后，翼型整体升力系数增加，后缘60%位置存在一个压力峰值，后缘区域压力系数分布整体光滑。

在进行结构求解时，需要将气动力插值到结构上，由于气动网格与结构网格不重合，需要建立气动力到结构的映射。本文采用了基于Wendland C4核函数的径向基插值技术构建了插值关系。由于结构求解时，边界条件直接作用在未变形结构上，而气动力则由假设的目标变形计算得到。本文基于变弯度后缘蒙皮长度不变假设，通过气动网格点在蒙皮的位置关系，构建了变弯度外形上的气动网格点到基础外形的气动网格点之间的保型映射，将作用在变弯度外形上的气动力投影在基础外形上，结果如图10所示。

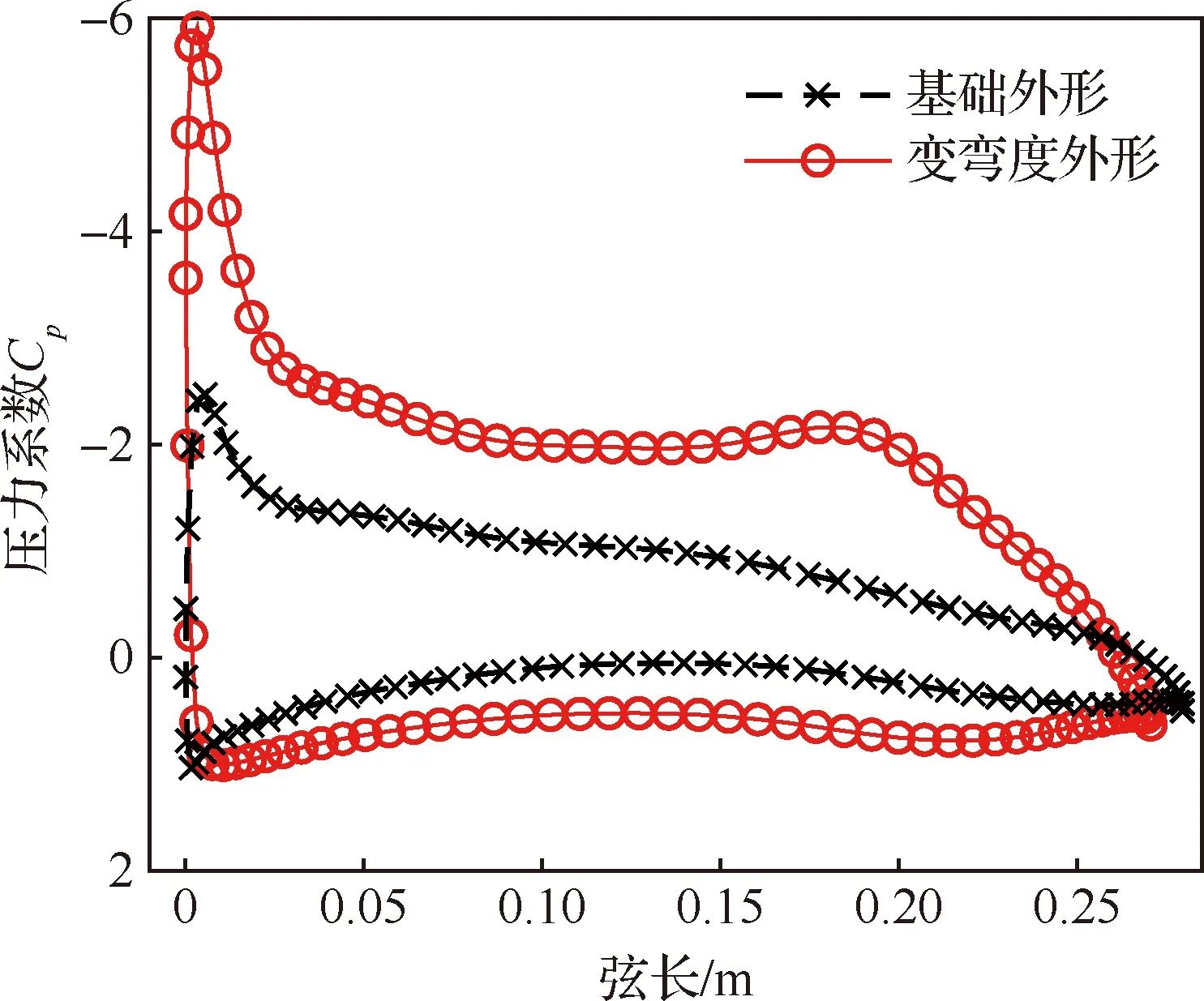
图9 在迎角为5°，使用面元法计算得到的机翼设计剖面的翼面的压力系数分布Fig.9 Pressure coefficient of the section to be design, calculated using panel method, at angle of attack of 5 degrees

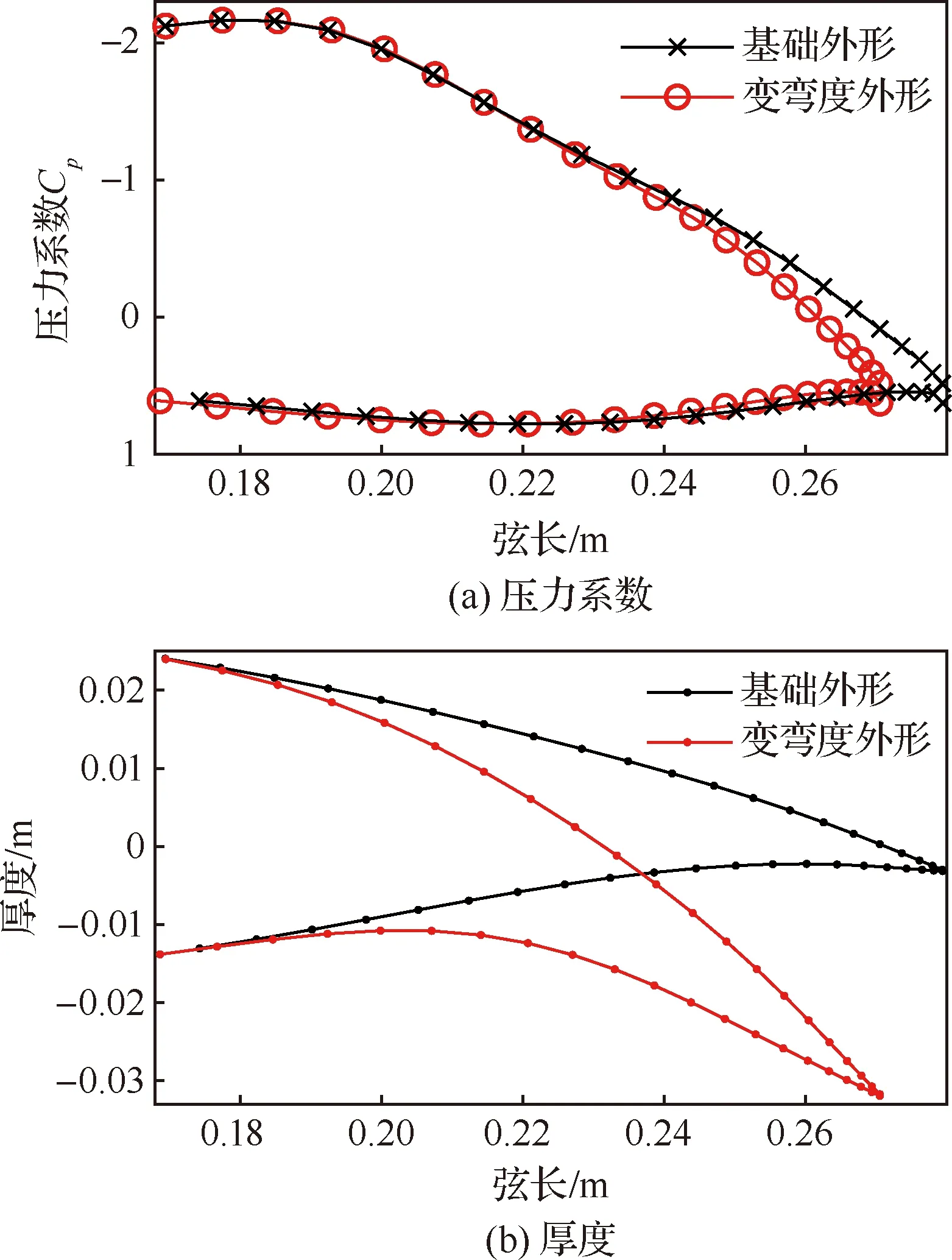
图10 将基于变弯度外形计算得到的翼型表面压力系数分布投影到基础外形结构上Fig.10 Pressure coefficient calculated based on morphing airfoil are projected to reference airfoil

2.4 结构求解器

本文采用了基于ABAQUS的几何非线性有限元网格划分与求解模块。有限元建模过程中：蒙皮采用S4R壳单元，为采用了减缩积分和大应变方程的4节点应力/位移的单元；梁则采用了B32三节点二次空间梁单元，能够很好模拟弯曲变形。内部的梁单元与蒙皮之间，采用绑定约束。考虑几何大变形引起的非线性静力学问题，采用迭代的方式求解。

2.5 优化问题

变弯度后缘由蒙皮、梁组成，在驱动力的作用下发生变形，风洞试验模型需要考虑结构的刚度、材料的许用范围、驱动器的驱动能力、变形的精度。通过研究变弯度后缘在基础外形时，受到气动载荷作用下的结构变形情况，可以优化结构的刚度。分析结构在多种工况下的结构内应力，可以使材料始终在许用范围内工作。变形精度则要求在驱动器能力范围内，使得变形与目标外形之间相似性最高。

影响以上约束和目标的因素可以分为2大类：结构拓扑与结构参数。结构拓扑是指后缘的蒙皮、梁之间的连接组合方式，这种连接组合方式在变形前后保持不变。而结构参数是指节点位置、蒙皮与梁的参数、驱动点的位置和驱动力的大小。本文在给定的结构拓扑的基础上，对变弯度后缘的结构参数进行优化。

本问题的设计变量有：蒙皮的厚度分布、梁的尺寸参数、梁的端点位置、驱动点位置、驱动力的大小和方向。其中蒙皮的厚度分布与梁的尺寸参数受到加工工艺的限制，驱动力的大小和方向则受到拟采用的驱动器限制，而其中梁与驱动点的位置需要引入额外的空间移动约束，以保证在优化过程中结构不产生干涉。如图11为梁端点的设计空间，其中黑色实线为蒙皮，黑色点为梁端点，红框为优化过程中梁端点的允许移动范围。该设计空间之间没有重叠，并且保持在翼型内部。

采用有效集法求解优化问题。该方法是一种基于梯度的优化算法，使用序列二次规划求解技术，并在每一次主迭代中求解一个二次规划问题。所需要的梯度采用数值向前有限差分方式获得，数值试验表明差分步长取2×10可以获得较高精度的结果。所有的设计变量均使用其设计变量的上下限进行归一化处理。优化器的目标函数与约束函数容差取为1×10。

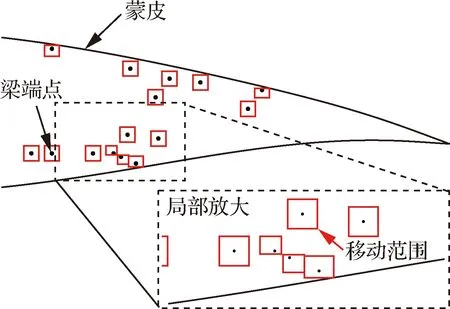
图11 应用于梁端点设计空间的约束Fig.11 Constraints applied to design space of internal beam vertexes

3 优化结果与分析

图12展示了用于结构参数优化的4种初始结构拓扑，分别命名为初始结构1、2、3和4，其中的初始结构4的下表面延长至占全翼型的55%弦长，便于在下表面较为平坦处安装直线滑轨。延长部分结构参数也包含在优化设计中。其中，初始结构1、2、3的弦长约为112 mm，最大厚度为38 mm，初始结构4的弦长为175 mm，最大厚度为45 mm。以上初始结构拓扑是综合考虑了基于连续体拓扑优化结果，基于先前的工程实践经验直接给定的。变弯度后缘设计中所采用的标记点和目标点在附录A中给出。

图12中的蓝色-绿色三角形为驱动点，黑色虚线为后缘基础外形，黑色实心点为标记点；红色虚线为目标变弯度外形，红色实心点为目标点。蒙皮的上表面根部固支，蒙皮的下表面能够沿着蒙皮切向滑动。驱动点和蒙皮之间通过梁连接，图中以蓝色实线表示，连接点为图中的红色菱形，位于蓝色实线上的红色点为梁的端点。初始结构的蒙皮厚度、梁的高度参数均为1.5 mm，初始驱动轴向拉伸位移7 mm。

柔性变弯度后缘的风洞试验模型利用基于低压力立体光固化(LFS)打印技术制造，能够实现0.05 mm的层厚精度，打印模型的最小允许壁厚为0.8 mm。采用FormlabsTough1500韧性树脂为原材料，该材料具有极强的韧性，能够承受循环加载，弯曲后能够快速回弹。经过二次光固化处理后的材料具有和聚丙烯相似的强度与刚度，其弹性模量为1.5 GPa，泊松比为0.45，抗弯强度为39 MPa。

本节将首先使用初始结构1，对比最小平方距离与Fréchet距离在衡量变弯度变形的形状精度上的差异。然后，采用优选的曲线相似性方法，利用本文提出的参数优化框架，对初始拓扑结构进行优化。

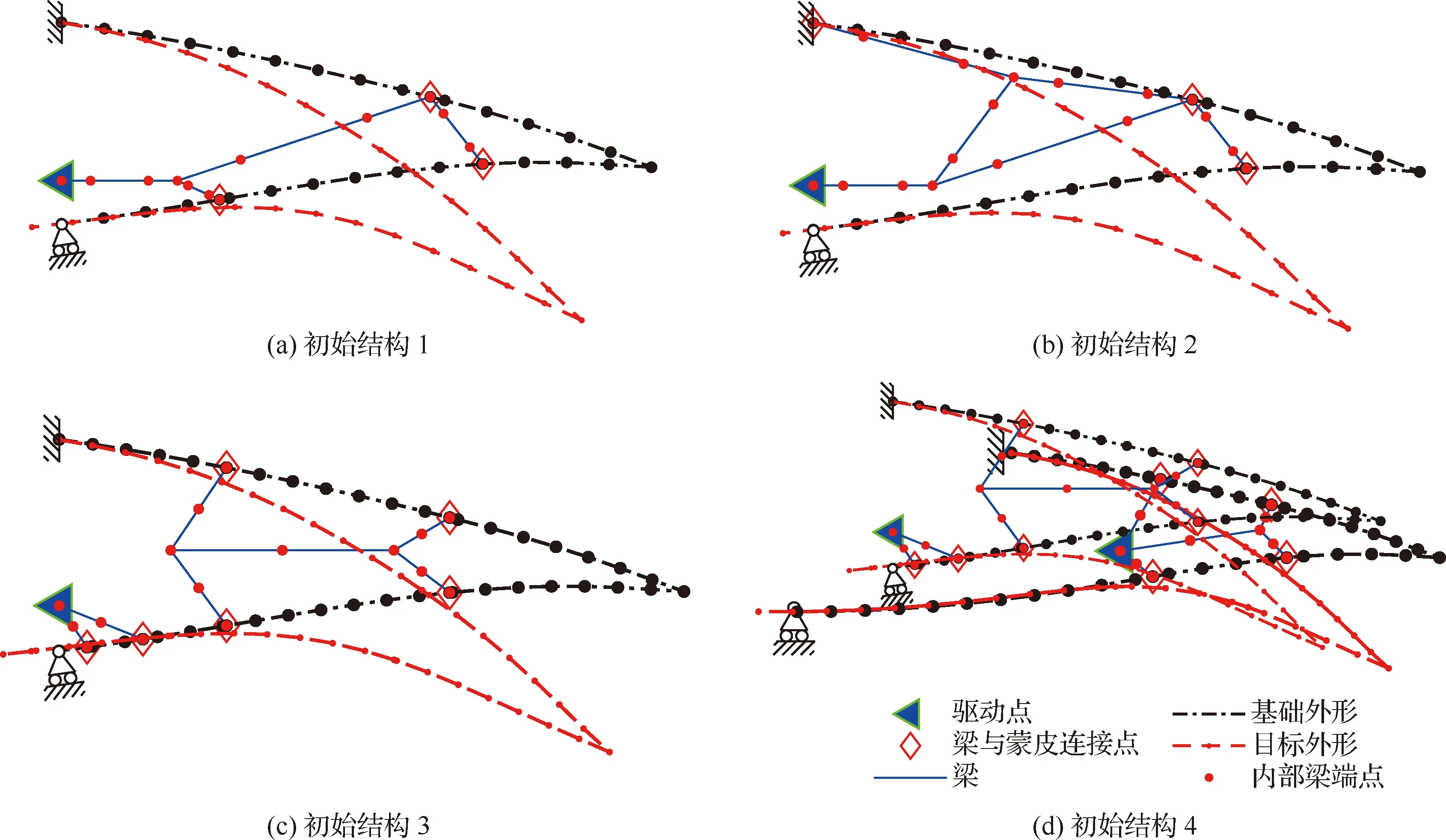
图12 4种初始拓扑结构的柔性变弯度后缘结构Fig.12 Four initial topology structures for compliant morphing trailing edge

3.1 对比：LSE距离和Fréchet距离

本小节采用初始结构1作为设计对象，研究了LSE距离和Fréchet距离2种曲线相似性描述方法对以变形精度为优化目标的柔性变弯度后缘结构参数优化设计的影响。

该问题的约束为：在不施加驱动位移，后缘只承受气动载荷作用时，其变形量小于给定阈值。选用较少的设计变量，只考虑蒙皮厚度、梁的尺寸参数和驱动力大小与方向。优化过程中，最大迭代次数设置为30次。图13展示了采用初始设计参数下的结构设计变形，该变形与目标变形之间的差距较大。

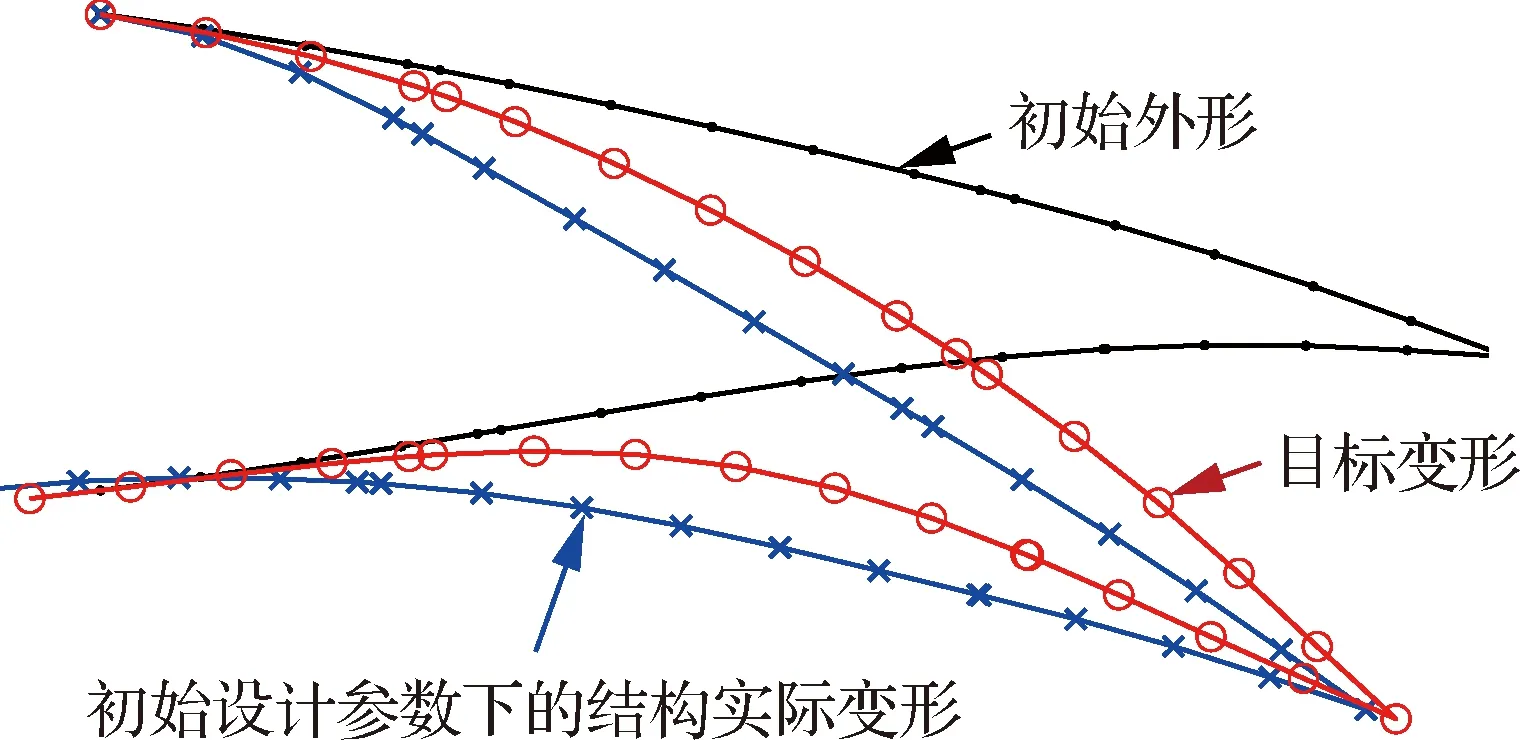
图13 施加驱动位移后，初始设计参数下的结构变形与目标变形Fig.13 Structural deformation under initial design parameters and target deformation after applying actuation

表4展示了采用LSE距离和使用 Fréchet距离的优化结果，均采用了初始弦长进行无量纲化。当采用LSE距离描述曲线的相似性时，初始优化值为8.419计数 (1计数等于10×10)，30次迭代后，目标函数降低到3.592计数，提高了57.3%。采用Fréchet距离时，目标函数初始值为26.186计数，经过11次优化后目标函数的变化小于10×10，程序自动终止，此时的目标函数值为2.768计数，提高了89.4%。图14对比了采用2种距离描述方式的优化迭代过程，绘制了目标函数随优化迭代步的变化，结果表明采用Fréchet距离优化迭代速度更快。对优化得到的结果进行交叉验证，即采用Fréchet距离评估基于LSE距离的优化结果，其值为19.345计数，相对于初始值提高了26.1%；而使用LSE距离来评估基于Fréchet距离的优化结果，值为1.702，交叉改进率为79.8%。表明采用Fréchet距离的优化效果较好。

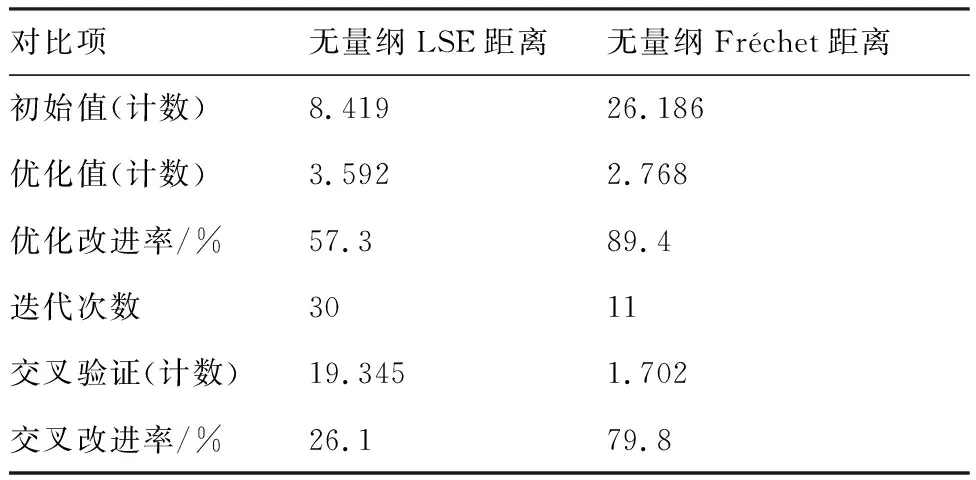
表4 使用LSE距离和Fréchet距离优化结果

进一步分析交叉验证差异的来源。图15为优化后的变弯度后缘变形前后外形。从上表面看，采用LSE距离为曲线相似度描述标准得到的变形与目标变形更为接近。但是，在弦长位置为0.2 m处的下表面出现了局部大变形。由于LSE距离通过捕捉的是曲线之间的平均差异，该局部大变形误差被其他区域变形精度的提升所掩盖。而Fréchet距离则是描述匹配点之间的最小的最大距离，在优化的每一步迭代中，始终以减小当前形状最大误差区域为目标，使得最终得到的变形误差较为均衡。

图16给出了采用了2种距离描述方式下的优化结构在驱动力作用下的变形，其中的T形桁条仅用于传递展向气动力，并不参与优化过程。能够看到采用LSE距离的后缘结构下表面由于蒙皮厚度达到了蒙皮厚度设计下限，在气动力和结构内力的作用下出现内凹。

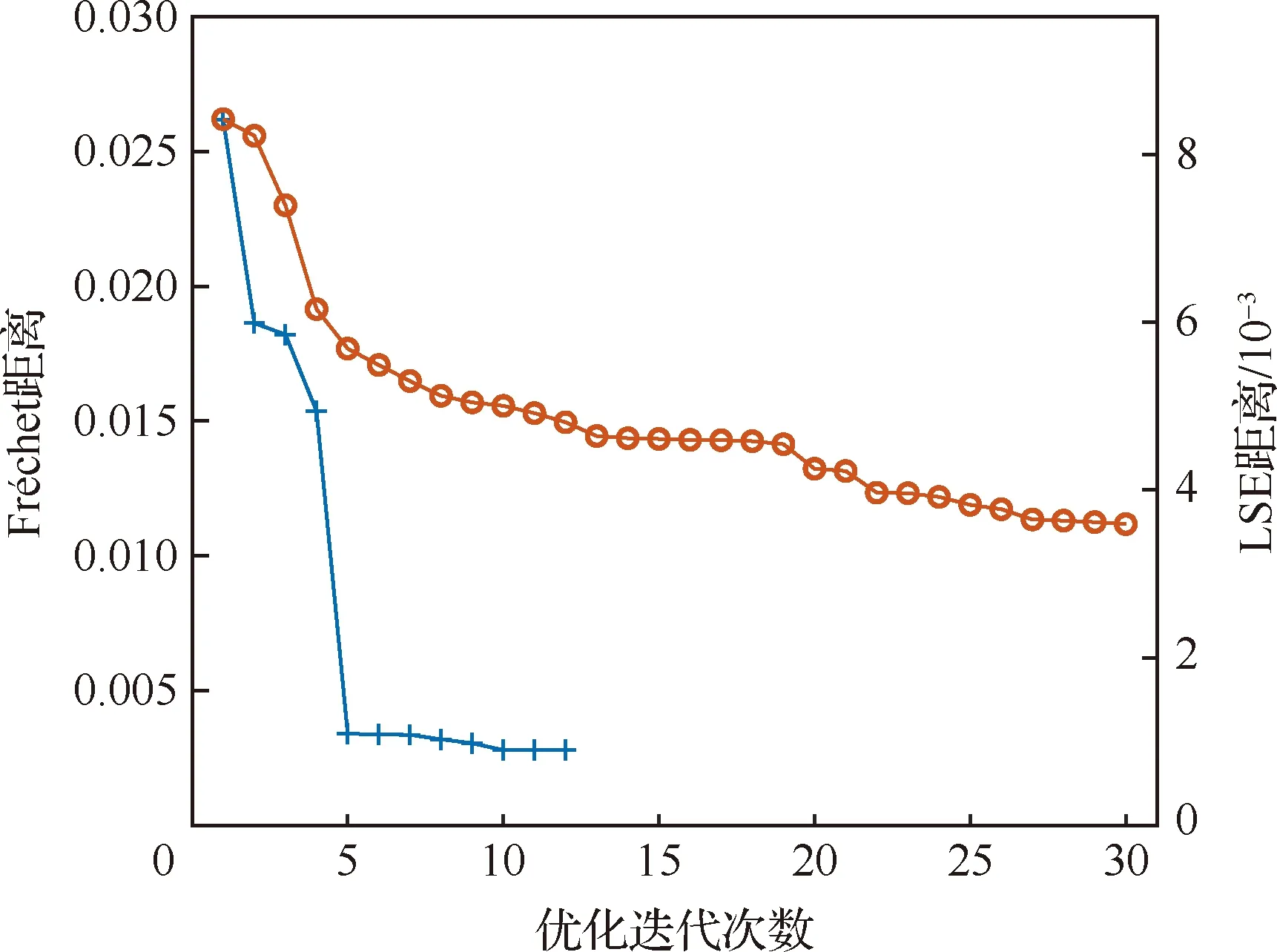
图14 对初始结构1，采用两种距离定义方式的优化迭代过程对比Fig.14 Comparison of optimization history using Fréchet and LSE distances for Case 1

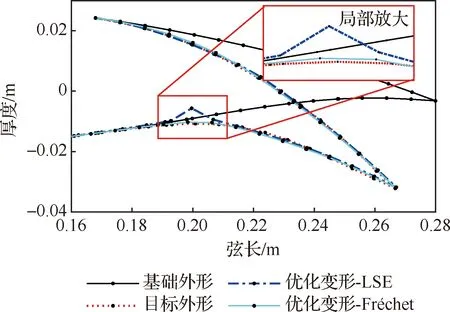
图15 对初始结构1，分别采用LSE距离和Fréchet距离得到的后缘变形Fig.15 Deformation of morphing trailing edge obtained by using LSE and Fréchet distance for Case 1

采用LSE距离的优化问题在达到最大迭代次数(30次)后自动终止，重新启动优化后，在第57步得到收敛结果，此时的目标函数为1.455计数，以Fréchet距离计算的目标函数为3.022计数。

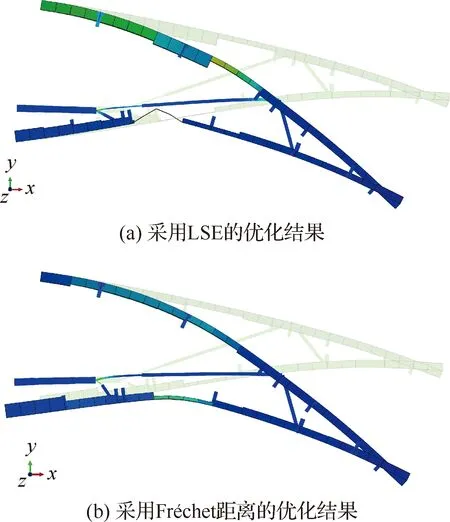
图16 对初始结构1，分别采用LSE距离和Fréchet距离的柔性变弯度后缘在加载后的有限元变形Fig.16 FEM Deformation of morphing trailing edge for using LSE distance and Fréchet distance

该仿真试验的结果表明：LSE不能捕捉到局部的噪声，而Fréchet距离可以很好地控制最大的变形误差，优化效率更高，所需迭代次数较少，并获得整体变形精度较高的结果。提示在变弯度后缘的优化设计中，可以综合利用2种曲线相似性测，首先使用Fréchet距离加速优化，再利用LSE距离对结果进行改进优化。

3.2 变弯度后缘结构参数优化

本小节对上文提到的4种初始拓扑结构，以降低Fréchet距离误差函数衡量变形后变弯度后缘到目标外形之间的距离为目标，对蒙皮厚度分布、梁的高度分布、梁端点的位置、驱动器的驱动点位置、驱动力的大小与方向进行参数优化。该问题的目标函数采用了初始弦长进行无量纲化，同时增加了蒙皮与梁单元的最大应力约束，要求结构应力小于极限应力的50%。

表5对比了多种结构的优化结果。初始结构1、3和4的初始目标函数分别为26.186、26.267和26.754计数，而初始结构2为16.295计数，表明初始结构2的变形精度优于初始结构1和3。对初始结构1进行参数优化，在迭代11次之后收敛，此时目标函数为2.793计数，较初始值提升89.3%。初始结构2在迭代12次后收敛，目标函数为2.848计数，较初始值提升82.5%。初始结构3一共进行了14次迭代，最终优化值为2.370计数，提升了91.0%。初始结构4进行了11次优化迭代，最终优化值为2.404计数，提升91%。结果表明，在使用Fréchet距离误差函数衡量变形后标记点到目标外形之间的距离时，多种初始拓扑结构均能够通过优化得到相似的变形精度，其中初始结构3的优化变形精度相对最高。

图17绘制了对比了拓扑结构1和拓扑结构2进行参数优化后的变形，均能相对达到目标外形，误差主要存在于局部区域。图18(a)～(c)展示了其中初始结构2、3、4的优化结果的有限元变形，结构设计区域应力均小于许用应力。初始结构3驱动点附近的结构超过了许用应力，该部分在结构详细设计中可以使用整体结构件替代，故该区域不在优化约束范围内。

表5 对几种初始结构的优化数据Table 5 Optimization results for several initial topologies

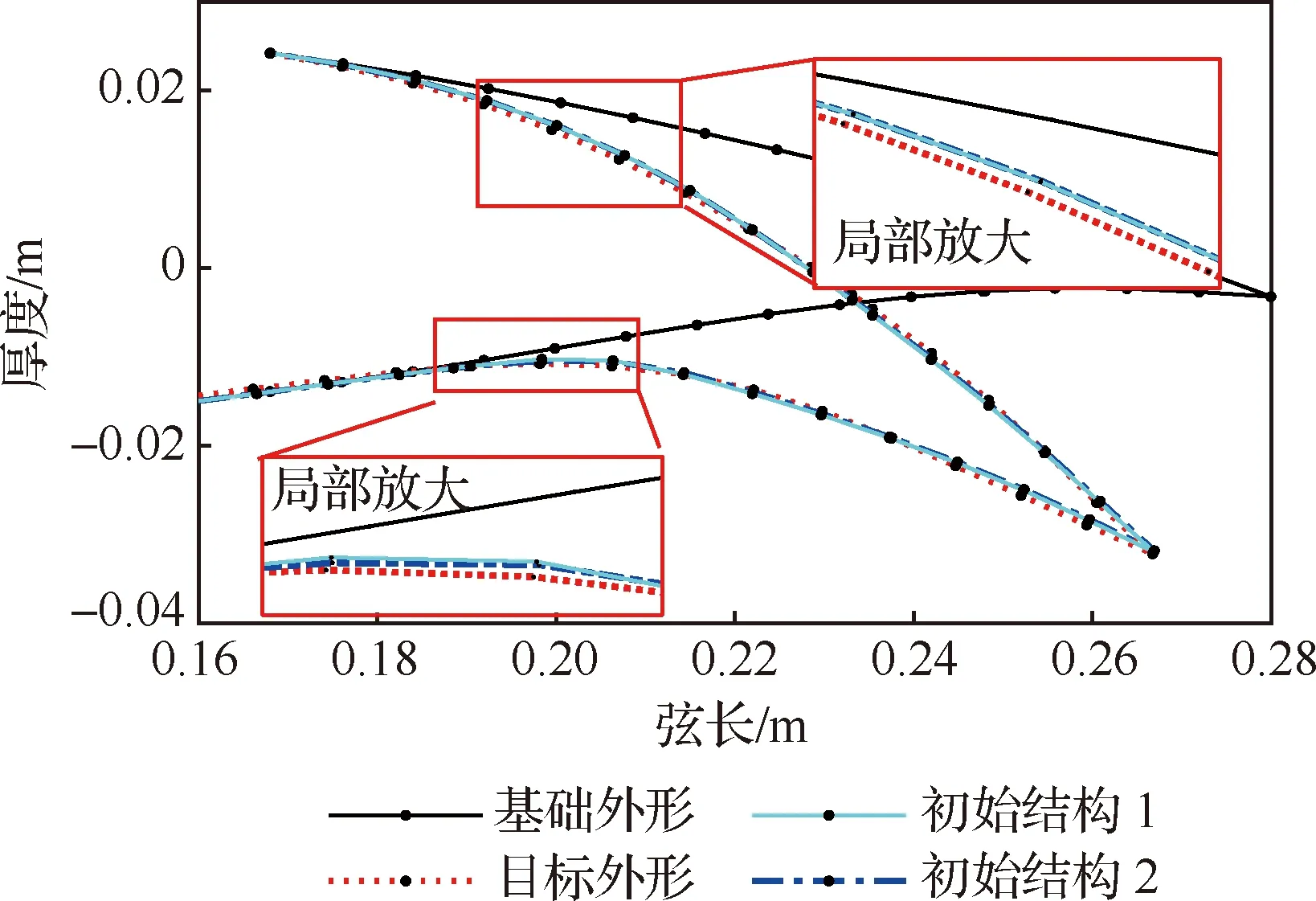
图17 对初始结构1和初始结构2优化后的变形Fig.17 Deformation after optimization for Case 1 and Case 2

为了验证采用Fréchet距离描述变弯度后缘变形的通用性，本文对初始结构4也采用了LSE距离进行优化。采用LSE距离后，初始结构4的初始目标函数为11.436计数，优化后降低到1.188 计数，变形精度提升了89.6%，变形精度提升略低于采用Fréchet距离优化结果。所需要的迭代步数为25次，是采用Fréchet距离优化所需要迭代步数的2.27倍。图18 (c)和(d)对比绘制了采用2种距离描述的优化结果。采用Fréchet距离优化结果上表面变形较为光顺，而采用LSE距离优化结果上表面出现了折角。

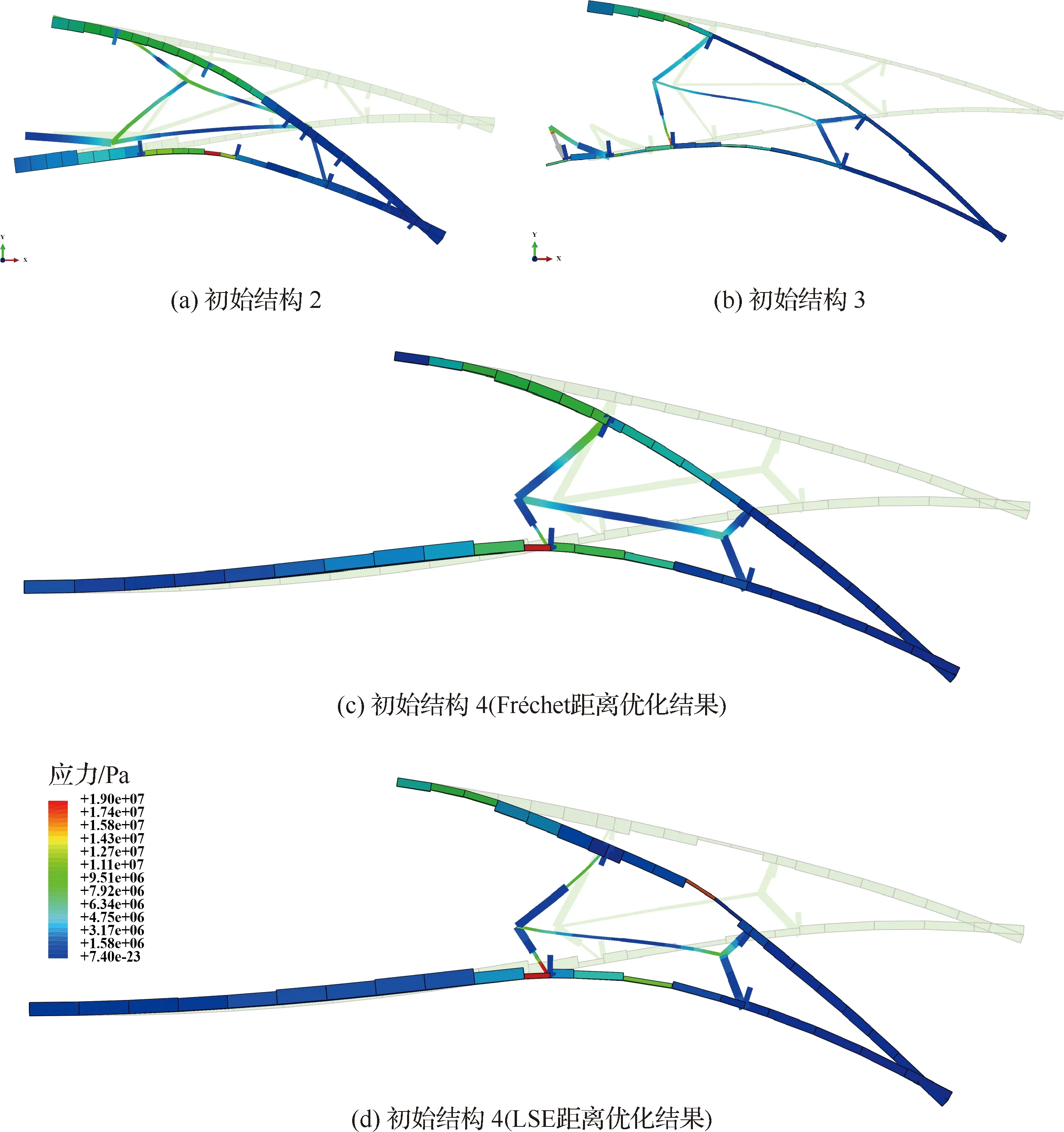
图18 对初始结构2、初始结构3和初始结构4优化后的非线性有限元变形Fig.18 FEM Deformation of morphing trailing edge for topology case 2, topology case 3, topology case 4(Fréchet) and topology case 4 (LSE)

4 模型设计与测试

基于优化后的初始结构4的拓扑形状和尺寸参数，设计用于风洞试验的翼段。该翼段主要由结构件与舵机系统组成，如图19所示，弦长175 mm，展长100 mm，高46 mm。结构件包括变弯度后缘和基座。在基座上安装有舵机系统，舵机通过连杆驱动变弯度后缘变形。变弯度后缘通过螺栓，在上表面根部与基座固支，通过下表面的直线滑轨与基座连接。该结构设计能够将变弯度后缘变形产生的内应力限制在该部件内部，不对机翼展向扭转变形产生影响。

所有的结构件均基于低压力立体光固化打印技术制造，采用AGF A26CHR 舵机系统驱动，驱动臂长1 cm，驱动力矩为100 N cm。图20为采用增材制造技术打印的变弯度后缘模型。该模型翼段具备有效的变形能力，如图21所示，其中的绿线为上偏时后缘形状，红线为下偏时外模线，黑色虚线为未变形时后缘外模线。无气动载荷作用下，能够实现下偏22.5°，上偏7.5°。优化时采用的是基于壳单元和梁单元的简化有限元，本小节采用三维实体单元，对所设计的数字样机建模，进一步分析气动载荷作用下的应力和变形特性。图22展示了采用实体单元建模的有限元分析结果，所用图注尺度与图18一致，分析时考虑了结构的几何大变形特性，最大应力出现在下表面，为16.7 MPa，满足结构设计要求，所需驱动扭矩为47 N cm。图23对比了采用实体单元建模的有限元变形与目标外形。

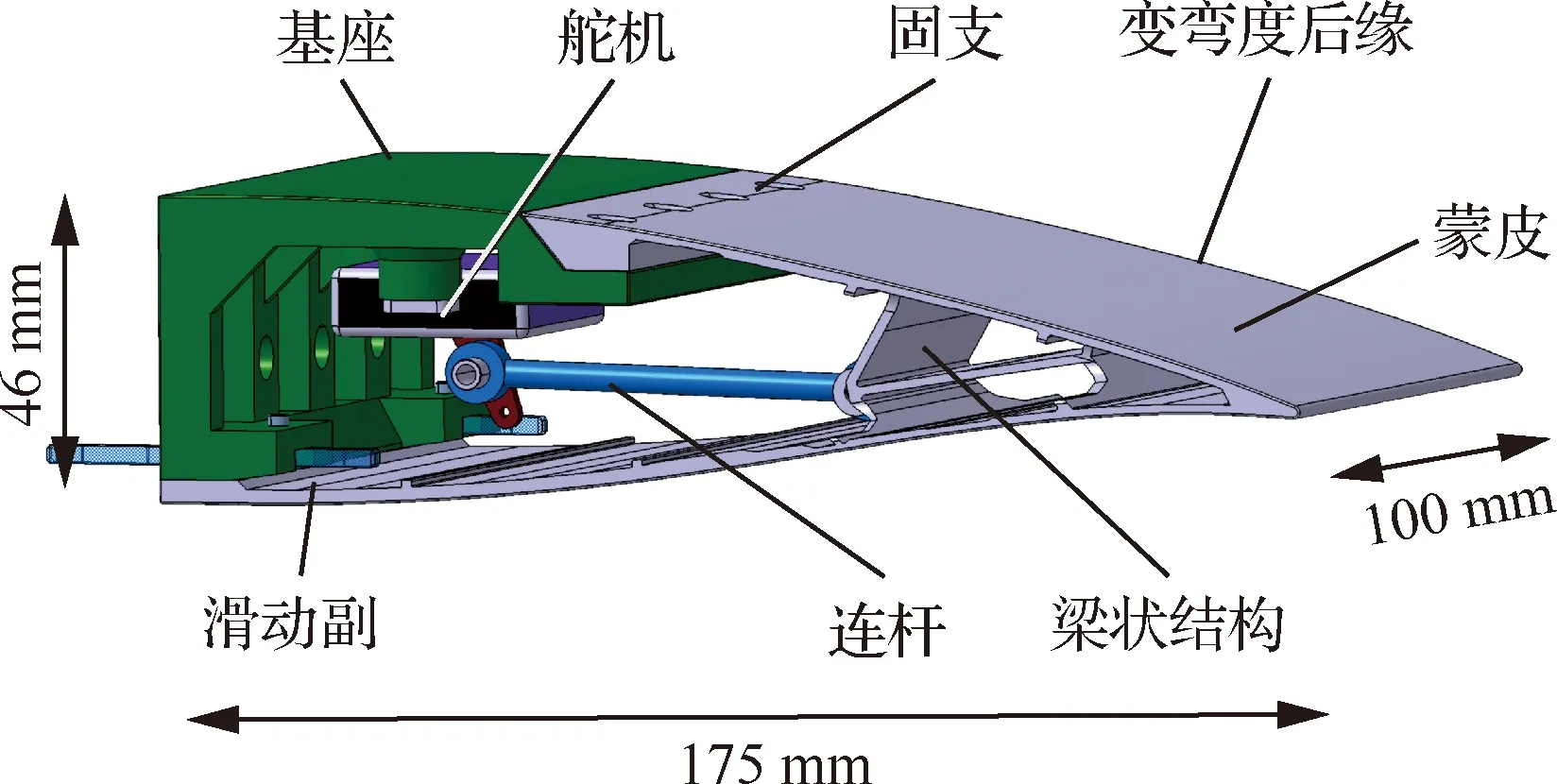
图19 变弯度后缘的数字样机Fig.19 Assembled CAD model of morphing trailing edge

图20 变弯度后缘模型Fig.20 Assembled model of morphing trailing edge

图21 变弯度后缘的变形能力演示Fig.21 Demonstration of deformation ability of compliant morphing tailing edge

本文仅考虑变弯度后缘翼段样件的设计与分析方法。下一阶段，将使用该方法制造变弯度后缘机翼，并在风洞中测试，对变形精度和承载能力进行验证。

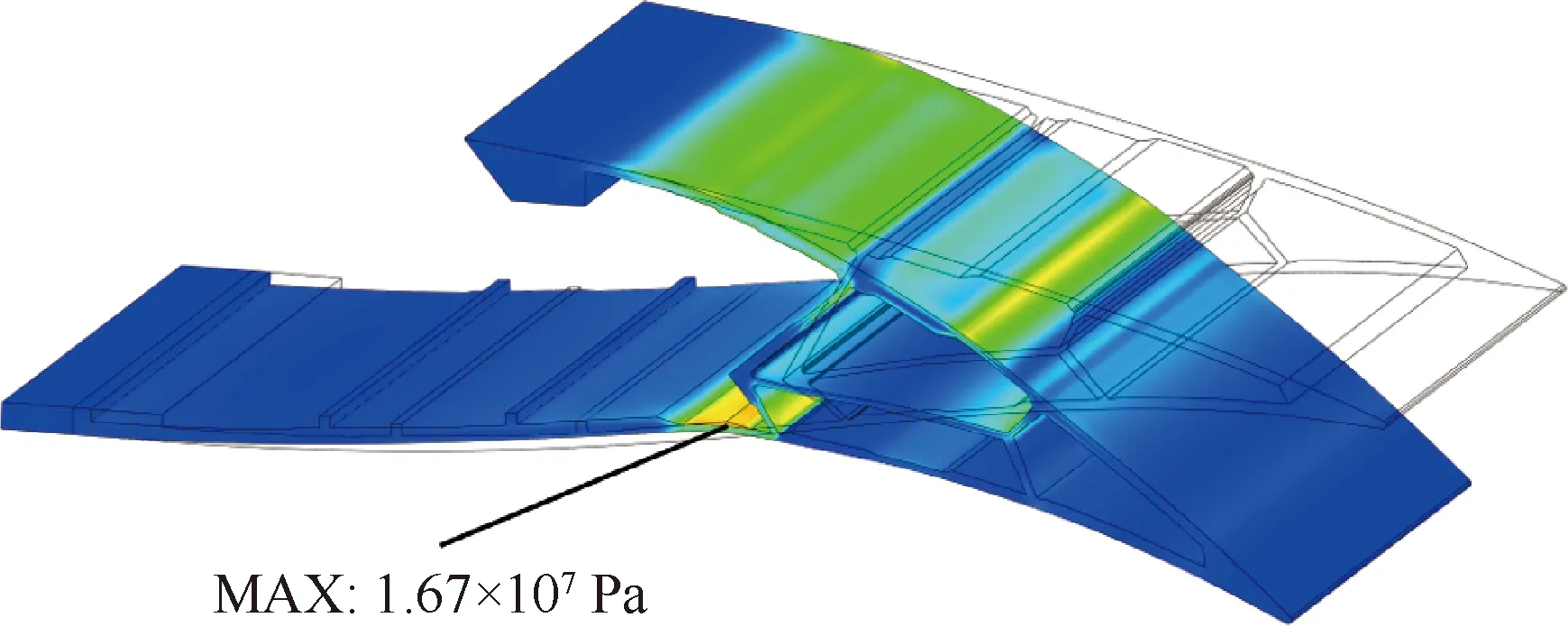
图22 变弯度后缘实体模型的有限元应力和变形分析结果Fig.22 Stress and deformation results of solid model of morphing trailing edge

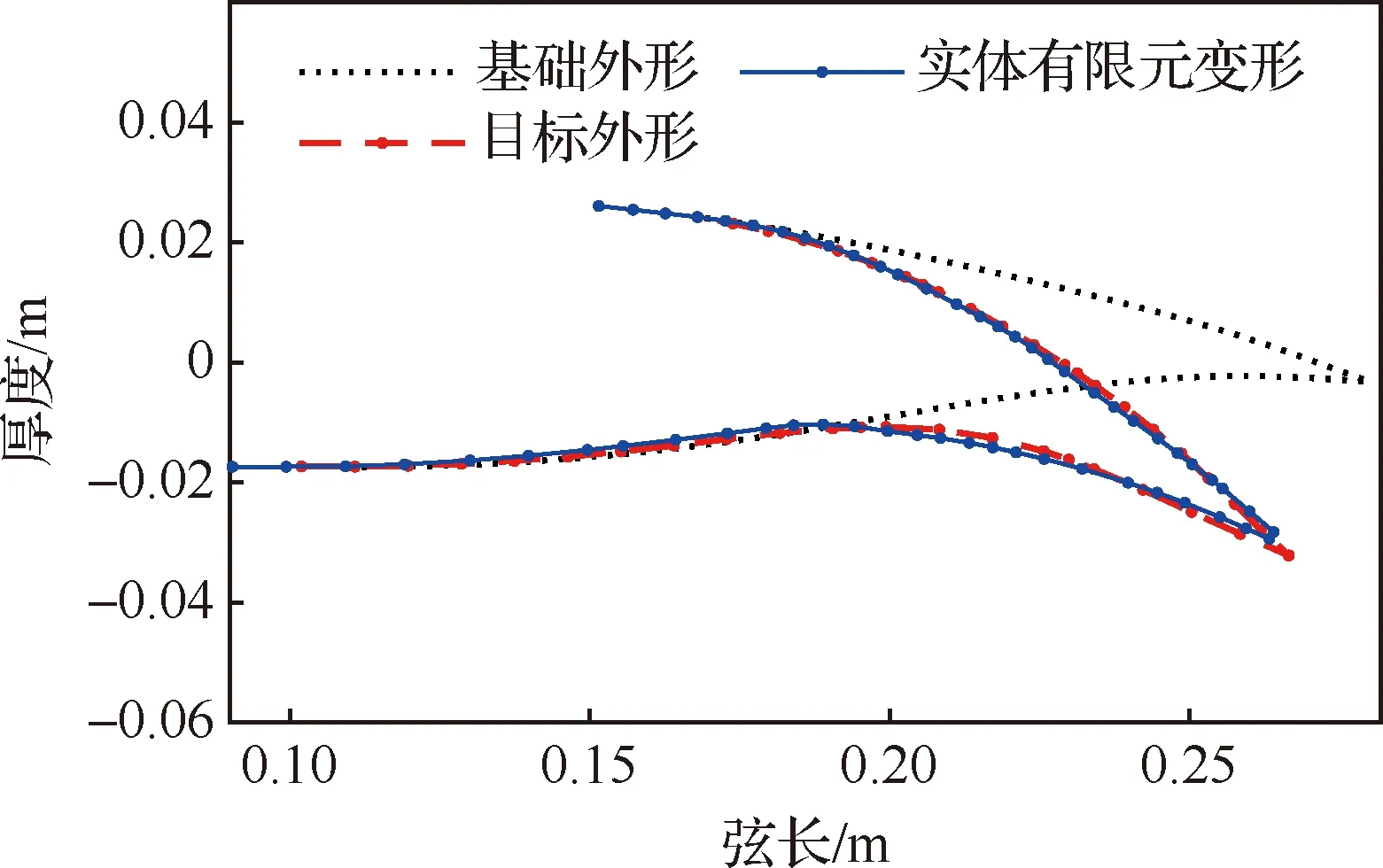
图23 实体单元变弯度后缘有限元变形与目标变形对比Fig.23 Comparison of deformation results of solid model with target shape

5 结 论

1) 提出了变弯度机翼的风洞试验模型的优化设计方法，该方法综合了变弯度外形设计、结构参数设计和驱动参数，能够较大幅度提高柔性后缘的变形精度。该方法也可以推广至变弯度飞行器的飞行试验模型设计。

2) 研究了影响描述变形精度的2种曲线相似性方式，包括LSE距离和Fréchet距离。结果显示：LSE距离不能捕捉到局部的噪声，而Fréchet距离可以很好地控制最大的变形误差，所需迭代次数较少，并能获得整体变形精度较高的结果。

3)使用本文提出的方法，对具有不同拓扑结构的初始设计进行优化设计，采用Fréchet距离，考虑气动载荷的作用，优化后初始结构1、2、3和4的变形精度分别为2.793计数、2.848计数、2.370 计数和2.404计数，均能够达到相似的变形精度。

4)基于优化结果，设计并采用整体增材制造方式实现了用于风洞试验的变弯度后缘翼段样件，无气动载荷作用下，具备下偏22.5°，上偏7.5° 的变形能力。