涡轮叶片累积损伤指数模型及服役可靠性评估

雷世英，孙见忠，刘赫

南京航空航天大学 民航学院，南京 211106

民航发动机热端部件的故障和失效是造成发动机性能退化及非计划换发的一个重要因素，其很大程度上制约了发动机整机的使用寿命。按照失效造成的影响严重性，可将热端部件分为A、B两大类。A类件又称为限寿件(Life Limited Part, LLP)，包括涡轮轴、涡轮盘等主要旋转件，其失效后会造成机毁人亡的严重后果，工程上一般通过安全性分析给定安全寿命，当达到规定的使用循环后进行强制报废，这种方法由于没有考虑个体发动机实际的载荷差异，寿命估计一般较为保守；B类件又称为关键件，主要是对发动机性能影响较大的结构件，如压气机/涡轮叶片、轴承等，其失效的后果没有A类件严重，但维修成本较高，发生故障时还可能造成较大的二次破坏，工程上一般采取视情维修的策略，通过评估剩余寿命来制订相应的维修计划，因此其寿命预测的准确与否对发动机的安全性和经济性有着重要影响，也是发动机寿命预测领域广泛关注的问题。如今发动机制造商和运营商对安全性和经济性要求越来越高，越来越趋向于在确保安全的前提下，尽可能地提高发动机的可用性，最大限度降低寿命周期运行成本，实现安全性和经济性的最大化。然而实际中要想实现寿命的准确预测是相当困难的，热端部件的使用寿命不仅受设计制造、材料工艺水平的影响，还与发动机的实际运行环境、使用方式以及维修模式等有着密切关联，这些多方面的因素使得预测的不确定性大大增加，预测精度很难满足实际需要。

目前对于关键件服役寿命的预测，总体方法上可以分为统计模型法、物理模型法和多模型、多数据融合的方法。在不具备零部件设计信息的情况下，一般使用可靠性分析的方法评估叶片的使用可靠性及剩余寿命，如An等采用贝叶斯方法融合外场可靠性数据，得到更新后的寿命分布来确定叶片寿命；Zaretsky等根据发动机外场使用数据分析了叶片的使用寿命，最终推导出一个估算叶片剩余寿命的计算公式；Li等采用模糊理论来表示涡轮叶片寿命预测中涉及的不确定性，利用线性融合算法对涡轮叶片的可靠性寿命进行区间评估。上述统计模型法需要提供大量的输入数据，但搜集数据的时间成本较高，具体的实验数据和现场数据也较为缺乏；除此之外，寿命可靠性预测涉及小样本问题，得到的结果反映的是相似使用条件下零部件使用可靠性的平均属性，难以体现单机状态下发动机自身及运行环境、运行载荷等方面的差异性。物理模型法则是建立在掌握了详细的材料参数与部件设计参数的基础之上，通过微观失效机理研究、计算流体力学与结构有限元法等分析手段，得到关键部位的应力、温度载荷，进而凭借失效机理对应的寿命计算模型，对寿命损耗进行评估，如Staroselsky等建立了基于晶体形态的弹粘塑性模型，考虑了材料滑移层的本构行为，并将其耦合到有限元模型中，使用半经验寿命预测模型估算叶片的剩余寿命；荷兰NLR中心和德国DLR中心等分别针对发动机涡轮叶片，通过实验设计(Design of Experience, DOE)方法构建了叶片温度和应力计算的代理模型，并考虑了蠕变和热机疲劳两种损伤模式来预测叶片剩余寿命；Zhu等通过引入种载荷参数来考虑涡轮叶片高低周疲劳损伤的耦合效应，使得预测误差的均值和标准差都达到了较高的精度；Brandão等等通过逆向工程得到了涡轮叶片的材料成分，借助有限元仿真比较了等温模型和非等温模型的蠕变寿命预测结果。上述物理模型的预测方法依托于材料力学、流体力学、热力学、有限单元法等基本理论，利用发动机的实际运行参数，获得叶片关键部位的应力和温度载荷谱，进而借助寿命损耗模型来评估涡轮叶片的剩余寿命。此类方法需要掌握发动机详细的设计数据，叶片的应力与温度载荷分析需要进行复杂的计算流体力学与结构有限元分析，但在模型计算时做了大量假设，会造成较大的预测不确定性。而多模型、多数据融合的方法则可以充分利用已有的多源异构数据，在叶片失效机理的基础上综合考量使用条件、运行环境等差异，相较于单模型方法能够提供更高的预测精度。Pillai等提出了基于有限元代理模型的多源信息融合方法，利用机器学习方法融合外场失效等数据，进一步降低预测结果的不确定性；Giesecke等结合发动机使用参数及运行区域大气环境条件建立贝叶斯置信网络用来预测叶片寿命损耗，以辅助决策叶片修理级别；Fu等考虑了微观结构准则和蠕变应变准则，并结合人工神经网络和改进的投影模型来评估使用中的涡轮叶片的剩余蠕变寿命，开发了一种基于材料基因工程的涡轮叶片在役蠕变剩余寿命的集成计算方法。

实际上，反映发动机关键件服役可靠性降级等行为特性的信息存在于多模态数据中，包括产品设计数据与使用维护数据，如产品几何参数、材料数据、状态监测数据、离线检测/检查报告、故障记录和大修报告等，贯穿产品寿命周期的不同阶段，如何充分利用这些多模态数据，实现多领域物理模型与数据融合，是提高服役发动机关键件寿命预测分析准确性的重要途径。本文以民航发动机高压涡轮(HPT)叶片蠕变失效为例，在蠕变失效机理分析基础上，同时考虑服役条件下的使用信息、状态参数及截尾失效时间等数据，提出的蠕变累积损伤指数模型实现了多模态信息的融合，对涡轮叶片服役可靠性进行评估，并预测其剩余寿命。现阶段外场数据获取有限，因此论文通过仿真数据验证提出方法的可行性和有效性，结果表明，本文方法比传统可靠性分析方法预测精度有显著提高。

文章的主要内容安排如下：第1部分主要介绍涡轮叶片的蠕变失效机理，阐述了蠕变的发展阶段、微观失效原理以及影响蠕变损伤的常见因素，并引入蠕变损伤评估模型；第2部分主要介绍叶片蠕变寿命计算的整个流程，包括发动机性能仿真、叶片应力计算、叶片温度计算及蠕变损伤评估等过程；第3部分介绍叶片蠕变累积损伤指数模型，给出了损伤指数模型的定义方法以及使用该模型进行剩余寿命预测的流程；第4部分为模型的仿真验证部分，使用实际发动机的状态监测数据进行了全寿命仿真，基于仿真数据验证蠕变累积损伤指数模型，预测HPT叶片的可靠性寿命，并与基准模型进行了结果对比分析；第5部分是对全文的总结以及后续工作的展望。

1 涡轮叶片蠕变失效机理

涡轮叶片作为典型的热端部件，长期工作在高温、高压、高转速的极限环境下，承受着离心载荷、气动载荷、温度载荷、振动载荷及高温氧化腐蚀的综合作用，其主要的失效模式包括：热机疲劳在内的低循环疲劳、振动引起的高循环疲劳、高温长时间载荷作用下的蠕变变形和蠕变应力断裂；高温燃气冲刷腐蚀和氧化以及外物损伤等。对于现代高涵道比民航发动机而言，其飞行过程平稳、飞行任务较为单一、飞行时间较长，这种工况下HPT叶片的蠕变损伤是决定其使用寿命的主要因素之一。同时，对于蠕变寿命的数值方法研究已经有了较为成熟的模型和方法，在工程实践中得到了广泛的应用。因此以叶片的典型失效模式—蠕变失效为例，来研究累积损伤指数建模以及外场数据融合的方法。

1.1 蠕变失效机理

蠕变是指工作在高温、高应力水平条件下的部件，随着加载时间的延长缓慢地发生塑性变形的现象。一般情况下，当材料的工作温度大于或等于其0.4～0.6倍熔点温度，且工作应力远低于材料的屈服强度时就会产生较为显著的蠕变变形。如图1所示，以蠕变时间为横轴，蠕变导致的材料变形量为纵轴，可以发现蠕变的发展一般分为3个阶段：① 初始蠕变阶段(→)，材料已发生一定形变，初始应变为，蠕变速率随时间逐渐降低；② 二次蠕变阶段(→)，蠕变速率基本保持恒定；③ 三次蠕变阶段(→)，蠕变速率随时间逐渐增加，直到蠕变时间发生蠕变断裂,此时变形量为。

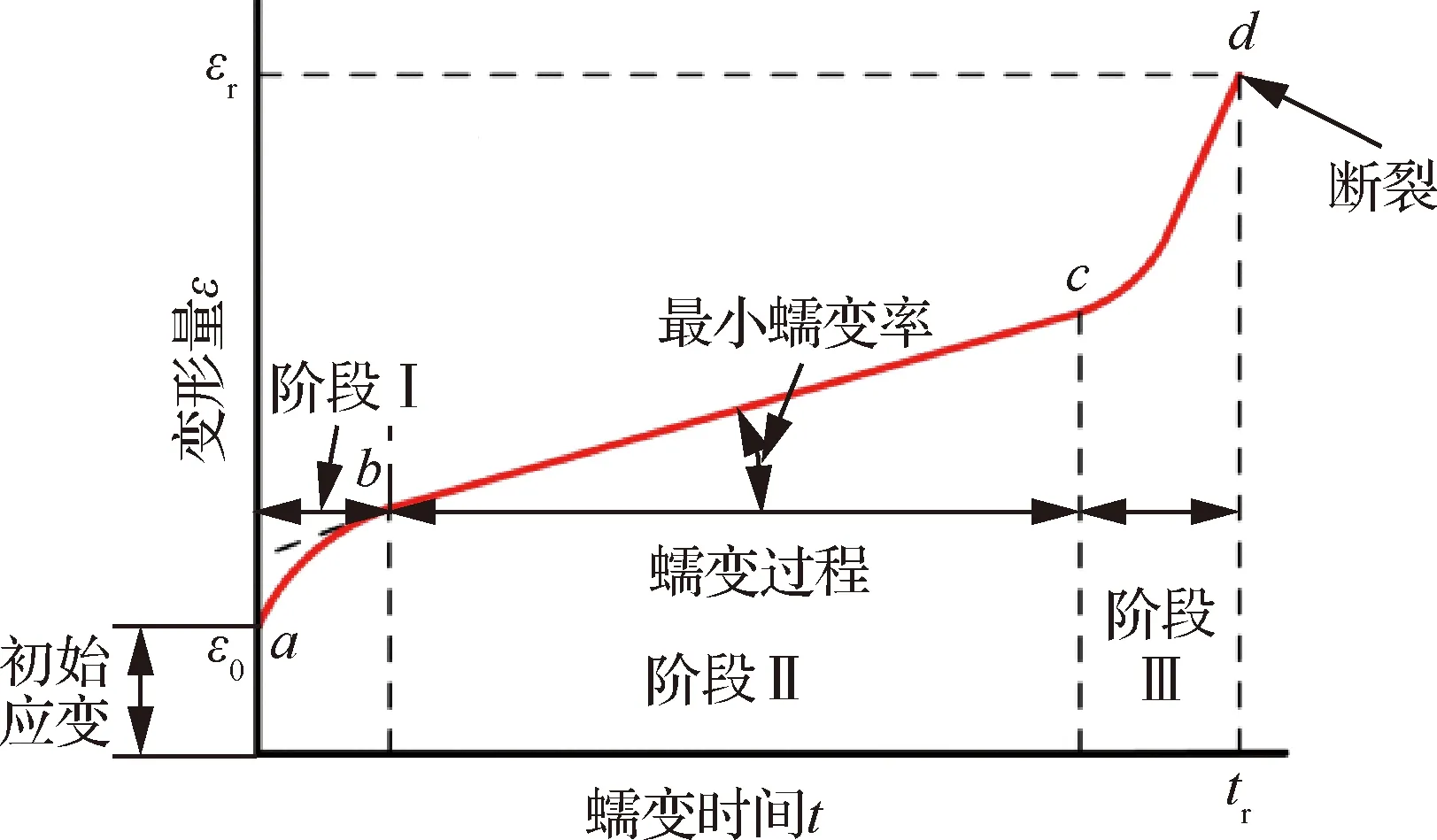
图1 蠕变发展阶段Fig.1 Development stages of creep

涡轮叶片的蠕变寿命对温度的升高十分敏感，研究表明，叶片的温度每升高10～15 ℃，其蠕变使用寿命将减少一半。同时，蠕变是一个依赖时间的热变形过程，叶片暴露在高温下的时间越长，其累积变形量越大。对于发动机涡轮叶片而言，工程上一般将蠕变损伤作为叶片应力、叶片温度和持续时间的函数。

1.2 蠕变损伤评估模型

叶片设计时所要求的持久强度一般在数万小时，通过长时间的试验获得相关的蠕变数据是不现实的，而想要精确地建立起预测蠕变损伤和剩余寿命的模型就越发困难。工程上一般使用由实验验证的蠕变持久方程来预测叶片的蠕变持久强度。目前，国内外较为成熟的叶片设计规范和手册普遍使用拉森-米勒(L-M)参数方程、葛-唐吾(G-D)方程、曼森-索柯普(M-S)方程、曼森-哈弗特(M-H)方程等方法进行蠕变寿命的计算和实验验证。选用工程上常用的L-M参数方程预测涡轮叶片的蠕变持久强度，该方法基于材料的蠕变试验数据，使用拉森米勒参数来表征材料在不同温度和应力组合下的蠕变断裂行为。针对叶片特定的某点，拉森米勒参数满足：

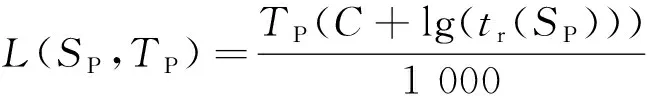
(1)

式中：为该点的温度载荷，K；为该点的应力水平，MPa；为蠕变断裂时间，h；为介于17～23之间的常数，一般情况取=20。同时，应力水平与拉森米勒参数之间的关系还可以用一个玻尔兹曼函数来表示：

(2)

式中：、、、是玻尔兹曼函数的参数。式(2) 可以看作是拉森米勒方程在全应力和温度范围内的扩展，模型的参数可以由材料在不同温度下的蠕变断裂实验数据和抗拉强度数据通过插值得到。由式(1)可以推导出在一定的应力、温度载荷作用下，持续时间内的蠕变损伤为

(3)

2 涡轮叶片蠕变寿命仿真计算

由于目前航空公司实际数据样本比较难以获取，基于某机队历史飞行数据，借助发动机性能仿真模型仿真得到整机关键站位的温度、压力、流量等性能参数，进一步基于HPT叶片的几何参数、材料参数，构建起叶片截面平均温度和参考点应力的数学计算经验模型，得到每个航班飞行任务中叶片关键部位的应力谱和温度谱，并基于L-M参数方程计算每个航班的蠕变损伤量。

2.1 涡轮叶片蠕变寿命计算流程

蠕变损伤计算涉及到温度和应力，需要进行相应的热分析和应力分析。按照分析维度的不同可划分为：考虑面平均或体平均的0D分析、考虑直线分布的1D分析、考虑平面分布的2D分析、考虑体分布的3D分析。随着分析维度的提高，模型中包含的单元类型和数量越来越多，建模的复杂程度逐渐提高，求解结果也会越来越趋近于真实情况。可见分析的维度从根本上决定了分析结果的准确性，但单纯增加分析维度会迅速延长模型的求解时间，模型的输入也越来越趋向于精细化，便利性大大降低。参考发动机部分设计公式，叶片关键部位温度和应力载荷历程计算用0D和1D的计算方法进行简化，在提高计算速度的同时，保证了一定的计算精度。所使用的蠕变损伤集成计算流程如图2所示，其中包含了用于中间环节计算和参数传递的子模型，同时也显示了不同子模型所需要的输入数据。

从图2中可以看出，蠕变损伤综合评估模型由4个子模型组成：

1) 性能仿真模型，仿真发动机HPT叶片进出口相关的气动参数和热参数，为叶片的温度和应力计算模型提供输入条件。

2) 叶片温度计算模型，对叶片进行温度分析，并为叶片应力计算模型提供输入条件。

3) 叶片应力计算模型，计算叶片参考点的应力。

4) 蠕变损伤计算模型，根据给定的飞参数据计算叶片蠕变累积损伤。

图2 蠕变损伤集成计算流程Fig.2 Integrated calculation process of creep damage

2.2 发动机性能模型

进行叶片的温度和应力的计算时需要提供叶片进出口的速度、温度、压力、流量等参数作为仿真计算输入的边界条件。这些参数往往不能由传感器直接测量，工程中通常使用一个能够反映发动机整机性能的模型来近似替代。基于发动机性能软件Turbofan Simulator，通过使用动态链接库的方法编程调用，建立能够匹配实际发动机的性能参数的部件级性能仿真模型。性能仿真实际上是对发动机的气路进行分析，通过调整相关的健康参数，使得发动机性能模型的输出与实测的气路参数相匹配。其中非线性模型由于精度较高的优势，最先是由Stamatis等引进到工业燃气轮机的气路分析当中,之后这种方法被推广到了航空发动机上，随着应用技术的成熟，最终开发出了民航发动机性能模型商业软件Turbofan Simulator。Turbofan Simulator能够实现海拔高度、环境温度、飞行马赫数、控制变量等运行参数同发动机整机各部位的温度、压力、流量等性能参数的快速匹配，同时可以调节表征发动机气路部件性能退化的健康指数，模拟发动机服役条件下的性能退化行为。性能模型包含了风扇(Fan)、低压压气机(Low Pressure Compressor, LPC)、高压压气机(High Pressure Compressor, HPC)、燃烧室、高压涡轮(High Pressure Turbine, HPT)和低压涡轮(Low Pressure Turbine, LPT)5个单元体，结构如图3所示。

性能模型输入参数包括飞行高度、标准大气温差、飞行马赫数等；蠕变损伤集成计算模型需要的性能模型输出参数包括高压转子转速、高压压气机进出口压力、HPT进出口温度等，详细数据见表1。

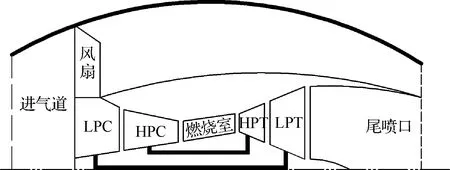
图3 发动机性能模型结构示意图Fig.3 Structural diagram of engine performance model

表1 性能仿真模型输入和部分输出参数

2.3 涡轮叶片应力计算模型

应力计算模型主要计算叶片参考点的应力，根据对应力成分的分析，将两种主要的应力来源纳入应力计算模型当中：由发动机转动的离心载荷引起的离心应力和由气体弯矩引起的气动应力。

为了较为全面地考核叶片的应力分布情况，针对某型民航发动机HPT涡轮叶片，首先通过逆向工程获取其计算机辅助设计模型，如图4所示。

图4 逆向工程得到的HPT叶片三维数模Fig.4 Three-dimensional model of HPT blade obtained by reverse engineering

进一步采用了一种伪二维解析的方法，按叶片高度取涡轮叶片的4个截面：叶根、25%叶高、50%叶高、75%叶高；根据叶片可能出现蠕变失效的危险点位置，每个叶片截面上分别取前缘最远点(Leading Edge, LE)、后缘最远点(Trailing Edge, TE)、叶背最远点(Blade Back, BB)作为计算参考点，并使用三维建模软件对叶片截面的几何尺寸进行测绘，截面选取的位置和计算参考点位置示意如图5 和图6所示。

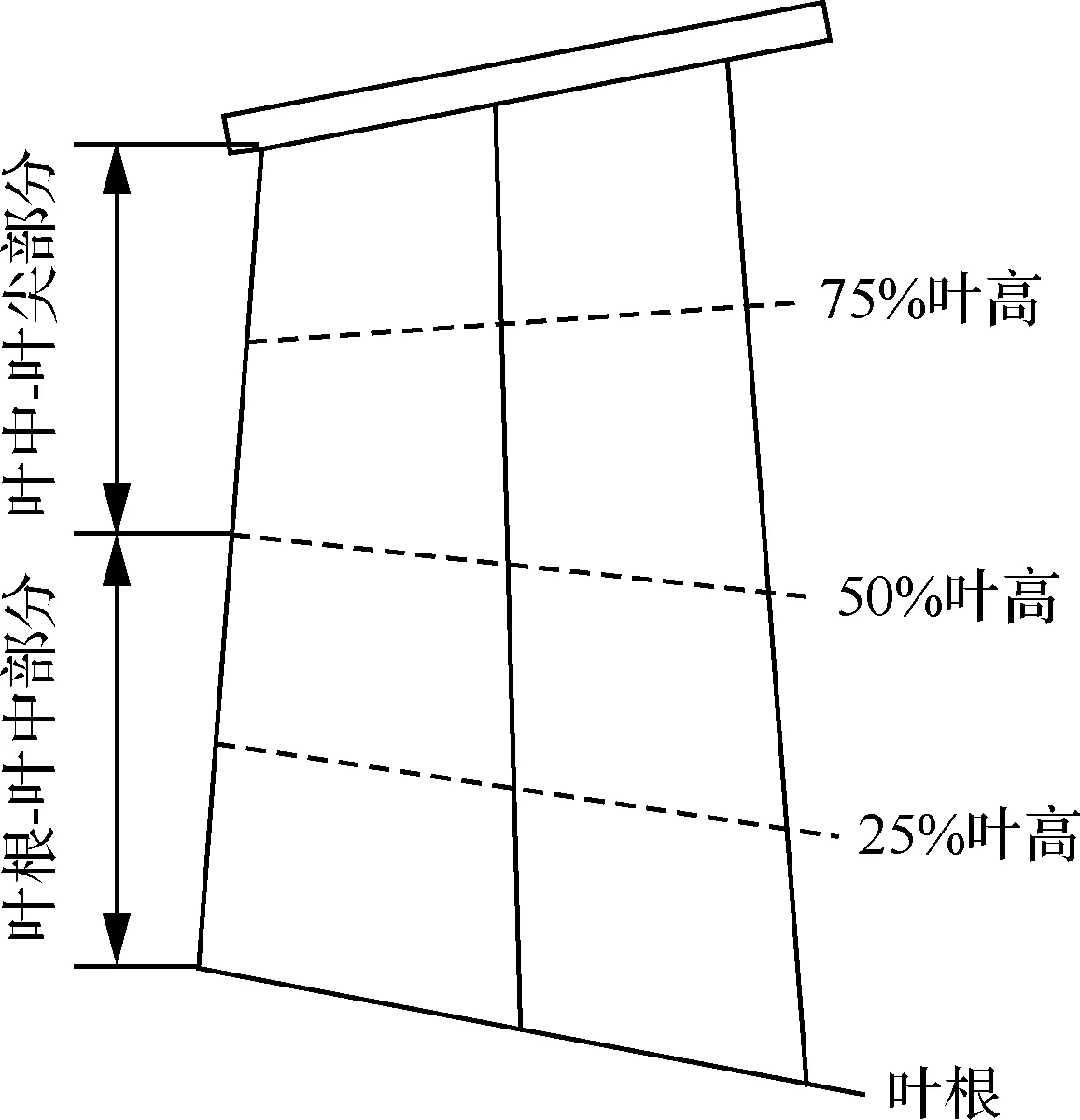
图5 叶片截面示意图Fig.5 Schematic diagram of blade section

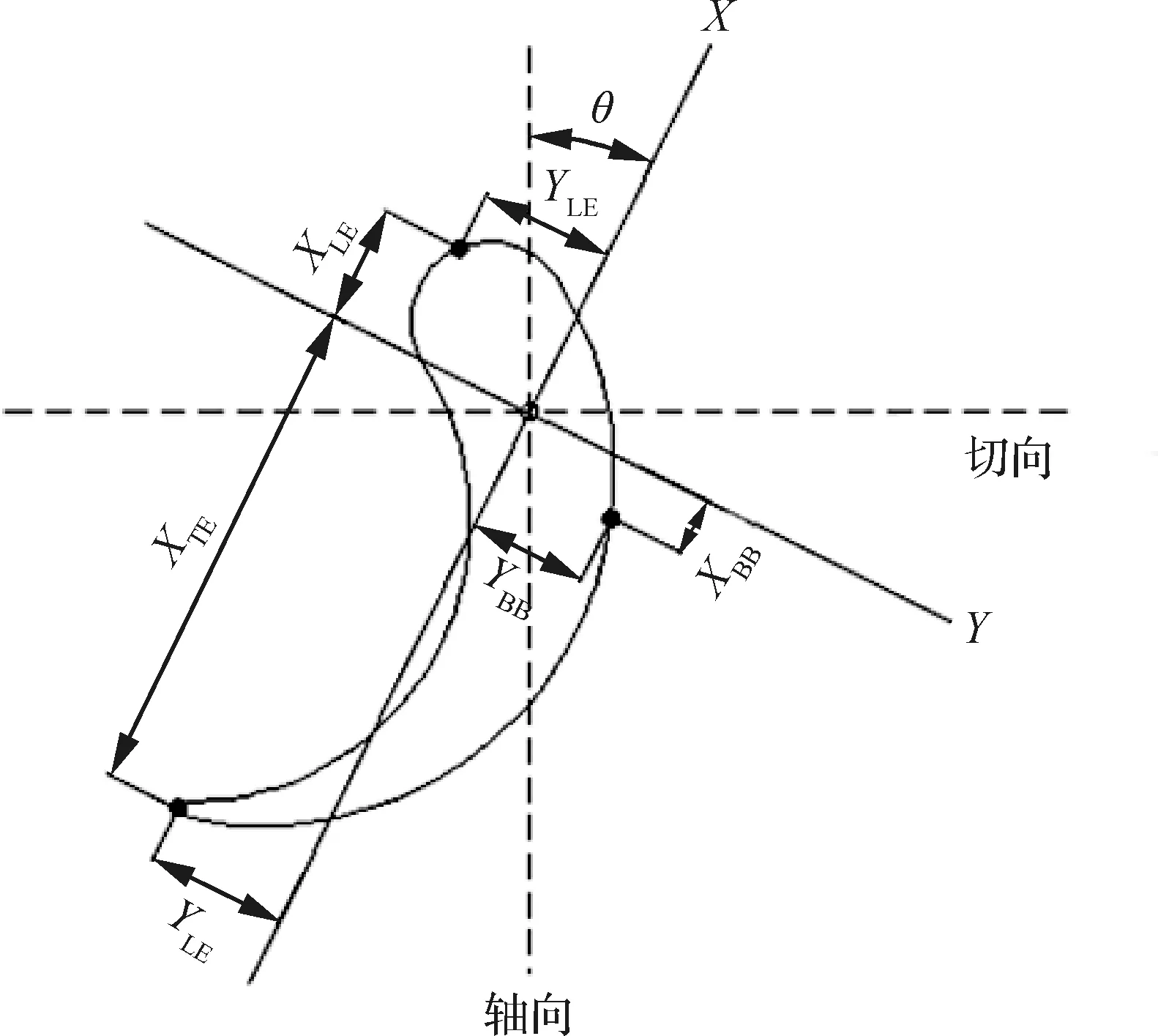
图6 叶片截面尺寸示意图Fig.6 Schematic diagram of blade section size

取叶根截面、50%叶高截面和叶尖截面，将叶片分为“叶根-叶中”和“叶中-叶尖”两部分，由于本文中的叶片型号没有叶冠，因此可近似认为叶尖截面的离心应力为0、25%叶高截面和75%叶高截面的应力可由叶根和叶中截面的计算结果进行插值得到。

叶根和50%叶高截面的平均离心力和离心应力分别为

=

(4)

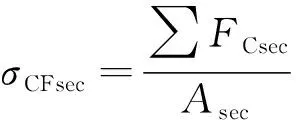
(5)

式中：为叶片材料密度；为计算截面和叶尖截面的平均面积；为截面到叶尖的高度；为旋转角速度；为“截面—叶尖”部分的重心到旋转中心的距离；为对应的截面面积。叶根截面和叶中截面的压力、弯矩分别为

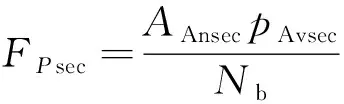
(6)

=∑()

(7)

式中：为截面截取的叶片段绕旋转轴一周在垂直于旋转轴方向投影形成的环形面积；为叶片段的平均静压差；为叶片的个数；为叶片段的重心到叶根的距离。

流经叶片进口和出口的气流速度变化会导致气体沿轴向和切向的动量变化，叶根和叶中截面轴向和切向的动量力以及动量弯矩分别为

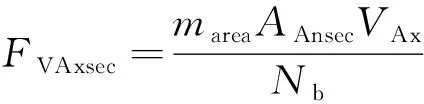
(8)

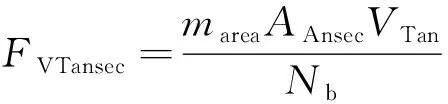
(9)

=∑()

(10)

=∑(Tansec)

(11)

式中：为投影的环状面积单位面积的质量流量；和分别为轴向和切向速度差。叶片截面的方向弯矩和截面参考点的弯矩应力分别为

=(+)sin+cos

(12)

=(+)cos-sin

(13)

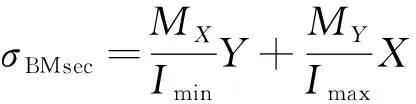
(14)

式中：为叶片安装角；和为叶片段产生的弯矩沿主轴方向的投影分量；和分别为截面参考点到截面惯性主轴的距离；和分别为截面的最大和最小惯性矩。叶片截面尺寸的定义如图6所示，、、分别代表叶片截面前缘、叶背最远点、尾缘到轴的距离；、、分别代表叶片截面前缘、叶背最远点、尾缘到轴的距离；为叶片安装角。因此，截面参考点的总应力可表示为

=+

(15)

2.4 涡轮叶片温度计算模型

温度计算模型主要用来计算叶片的基体温度，本文中涉及的叶片型号主要冷却方式为气膜冷却，采用1D的温度计算模型不仅能反映蠕变失效的点位，结合上文中的应力计算结果和后续的蠕变损伤评估结果，还能反映不同位置处温度和应力的不同组合对蠕变损伤的影响。类比于应力计算模型，计算温度时将叶片按照叶片长度的0～25%、25%～50%、50%～75%、75%～100%依次划分为4段，从叶根到叶尖，把前一段的冷却气体出口温度作为后一段的冷却气体入口温度，计算得到叶片叶根、25%叶高、50%叶高、75%叶高共4个截面的平均温度。

计算时首先需要指定径向温度分布因子(Radial Temperature Distribution Factor, RTDF)，RTDF的值一般不超过0.2。同时在进行温度计算前，需要做如下假设：

1) 由于叶片的旋转效应，叶片最高温度的位置会从叶片中部向叶尖区域转移(图7)，因此假设最大燃气温度位于距离叶根75%叶高的位置。

2) 叶根和叶尖的燃气温度为最低燃气温度。

3) 从75%叶高到叶根的温度降低是线性的。

4) 从75%叶高到叶尖的温度降低是线性的。

最大和最小燃气温度为

=+

(16)

(17)

式中：为涡轮进口温度；为燃烧室温升；为径向温度分布因子。叶片段的平均金属温度为

=-(-)

(18)

(19)

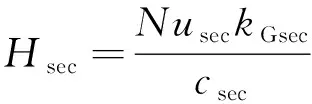
(20)

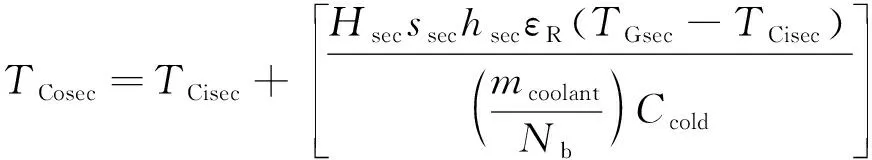
(21)

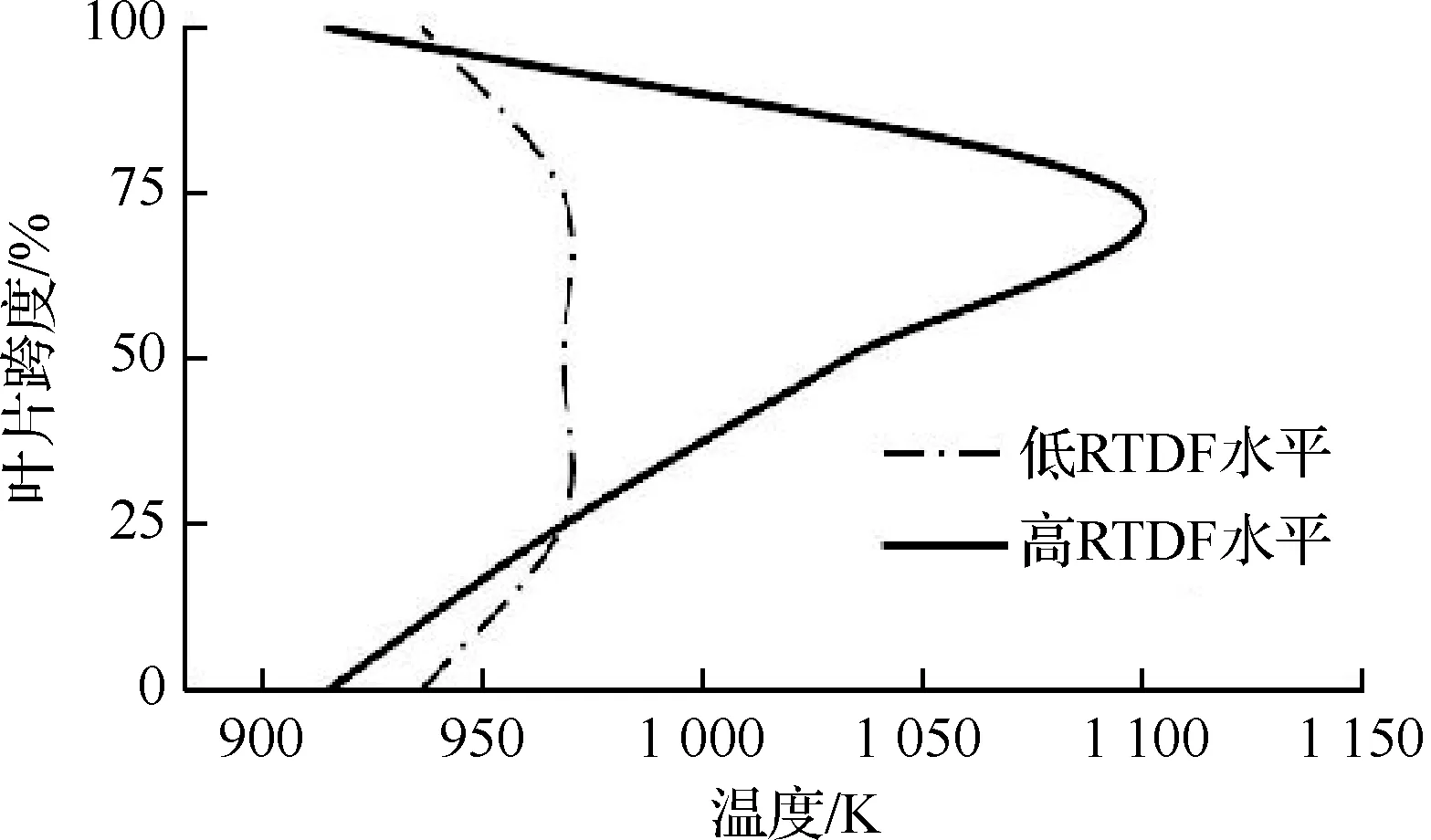
图7 径向温度分布Fig.7 Radial temperature distribution

2.5 蠕变损伤评估模型

使用上述的温度、应力计算模型，每次计算可以得到叶片4个截面、每个截面3个参考点共12个点的温度和应力情况，由于叶片的叶型尺寸和工作条件决定了叶片的蠕变失效位置，因此蠕变失效最先出现在叶片的哪个位置并不固定，表2给出了某航班爬升工况下的温度和应力计算结果。

从表2中可以看出，截面温度随着叶片跨度的增加而逐渐升高，截面应力随着叶片跨度的增加而逐渐减小；在同一截面内，前缘参考点应力最大，尾缘参考点应力次之，叶背参考点应力最小，但应力水平差距较小。综合式(1)和式(2)可计算出表2中温度和应力对应的蠕变寿命，见表3。

表2 温度和应力计算结果Table 2 Temperature and stress calculation results

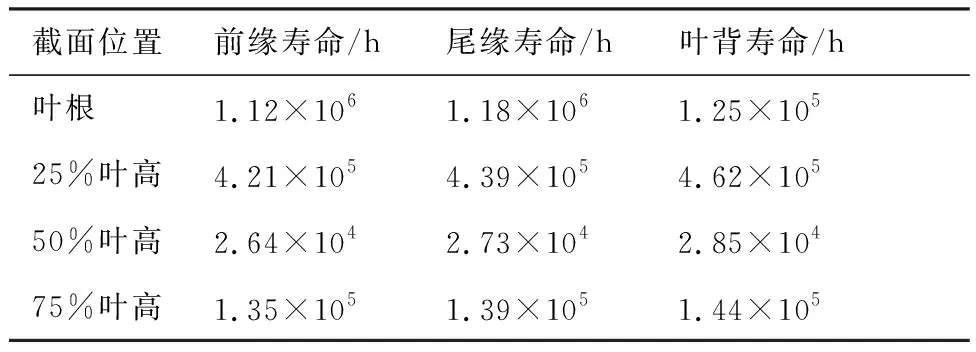
表3 蠕变寿命计算结果Table 3 Creep life calculation results

从蠕变寿命计算结果中可以看出，50%叶高截面的前缘蠕变寿命最短，可以作为整个叶片的危险点。由式(3)可求出所有时刻对应的单位时间危险点蠕变损伤，之后遵循Minner线性法则，对一个飞行循环持续时间内的蠕变损伤进行累加，即可得到某个飞行循环对应的累积蠕变损伤：

(22)

式中：为在第个飞行循环、第个载荷状态下叶片的蠕变持久寿命；为在第个飞行循环、第个载荷状态下的持续时间；即为第个飞行循环对应的累积蠕变损伤。

3 涡轮叶片蠕变累积损伤指数模型

在飞机服役过程中，即使有两台发动机的飞行任务剖面完全一致，甚至于涡轮叶片表面的载荷历程完全一致，但由于实际的运行环境和操作条件等因素不可能完全相同，最终导致两台发动机的叶片使用寿命存在较大差异。传统的基于统计分布的方法虽然可以拟合出叶片失效样本整体的寿命分布，但很难基于历史的环境载荷对单机状态进行有效的寿命评估；而对于非设计单位而言，叶片材料数据、三维模型等资料难以获取，使得精确的有限元仿真计算难以进行，其计算结果很难反映出实际情况下的不确定性因素对寿命的影响。

对于发动机来说，飞参是最常见的发动机动态时序数据，可以从机载设备上直接获取，其次它作为传感器数据，本身就集成了运行环境、运行载荷等因素的综合作用，直接反映了发动机的使用历程，体现了单机运行条件。将这种动态数据纳入分析的范围也可以更好地解释发动机个体剩余寿命的差异性。由第1部分蠕变损伤评估模型可知，叶片的温度和应力直接决定了叶片的蠕变损伤，而高压转子转速直接决定了叶片的离心应力；排气温度通常与叶片温度有着较好的相关性，这两种时序数据作为常见的状态监测数据记录在机载快速存储设备中，非常容易获取。因此基于动态时序数据和,定义了一种HPT叶片的蠕变累积损伤指数模型，用于表征使用环境载荷等参数对蠕变寿命分布的影响。通过对Ⅰ型截尾数据累积损伤指数失效分布相关参数的最大似然估计，得到基于累积损伤指数的失效分布函数，并在第4节对叶片寿命进行评估。

3.1 累积损伤指数模型

累积损伤指数(Cumulative damage index, CDI)描述了动态环境载荷因素对观测样本失效时间分布的影响，环境载荷历程称为样本的动态协变量过程。假设随机变量表示样本的失效时间，随机变量表示截尾数据的失效标志位(=1表示观察结束前样本已失效；=0表示在观察结束时样本未失效)，()表示样本空间内的个体在一段时间间隔下的协变量集合。=(,,())为可观测到的组合随机变量，对于样本内的第个样本个体，具体数据可表示为(,,()),=1,2,…,，其中为样本总量；表示第个样本个体的失效时间；表示第个样本个体的失效标志位；()表示第个样本个体失效时间内的协变量过程，则时间内的累积损伤指数定义为

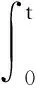
(23)

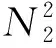
图8 叶片温度与排气温度散点图Fig.8 Scatter diagram of blade temperature and exhaust temperature

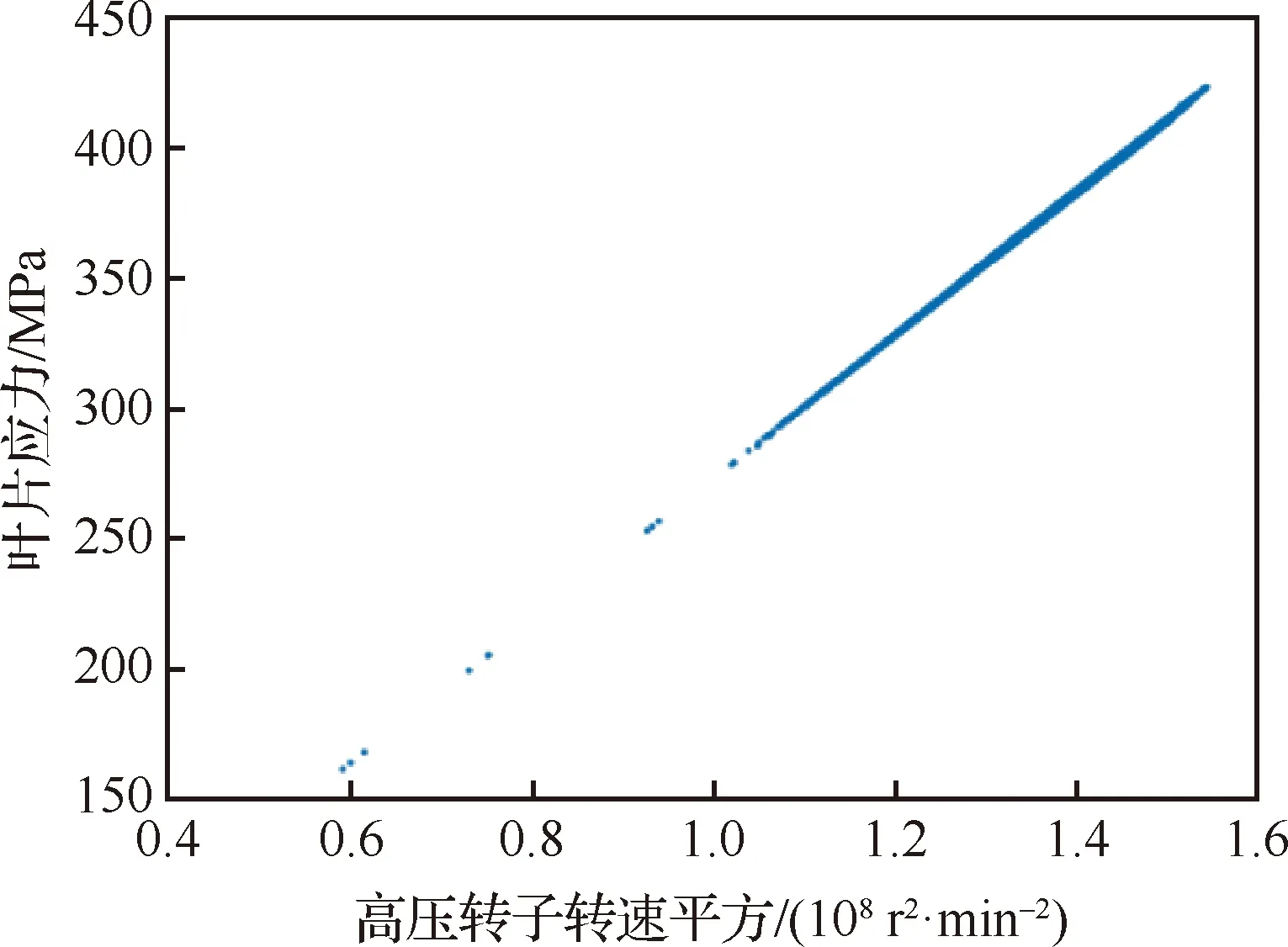
图9 叶片应力与高压转子转速平方散点图Fig.9 Scatter diagram of blade stress and high pressure rotor speed

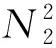
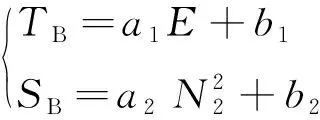
(24)

式中：、为线性回归的回归系数；、为常数项。忽略、并将式(24)代入式(2)和式(3)中可得：

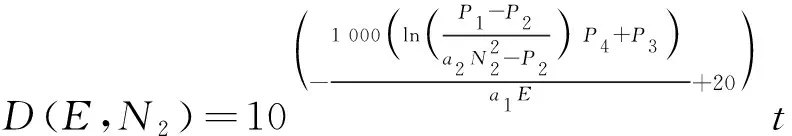
(25)

忽略式(25)中的次要常数项，并作进一步化简

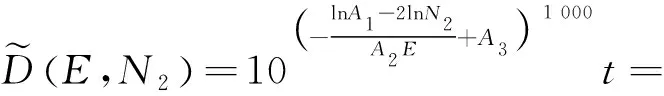
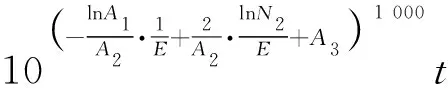
(26)

式中：、、为相关的系数。综合上述分析，使用协变量和的函数形式来定义蠕变损伤指数：

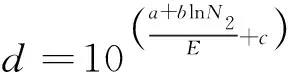
(27)

式中：和是损伤指数的相关未知参数；=8为给定的常数项。进而一段时间内的蠕变累积损伤指数()可表示为

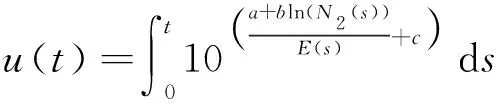
(28)

在失效时间内，每个样本依据随机的协变量过程(∞)产生对应的累积损伤指数，当其达到一定的阈值时样本失效，假定的累积分布函数(,)服从威布尔分布，转化为极值分布后满足：

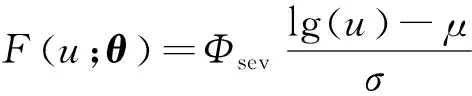
(29)

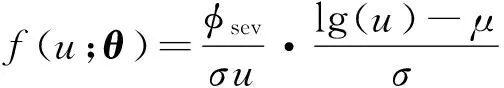
(30)

式中：为极值分布函数；为极值分布概率密度函数；=(,)′为极值分布的特征参数。与失效时间之间的关系为

(31)

故的分布函数和概率密度函数分别为

(;,)=((;,());)

(32)

(;,)=′(();)((;,());)

(33)

3.2 模型参数估计方法

涡轮叶片的服役寿命普遍在上万小时，实际当中一般统计截止时间内的飞行循环数作为叶片的寿命信息，如果截止时间内叶片失效，则失效标志位记为1；否则失效标志位记为0。失效标志位和截止时间内的叶片寿命信息一同构成失效样本，这类数据也称为截尾数据。截尾数据中的失效时间是一个含有连续部分和离散部分的混合随机变量，综合式(31)和式(32)可以推导出其对应的似然函数为

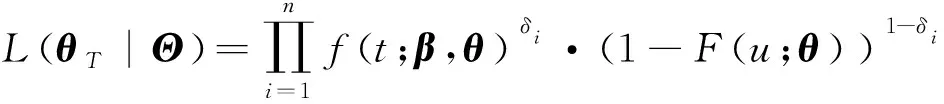
(34)

式中：=(,)′和=(,)′是似然函数中的待估计参数。结合式(28)、式(31)、式(32)和式(34)，通过迭代求解可以估计出参数、、和的值。

3.3 剩余寿命预测方法

叶片的剩余寿命是基于当前的使用寿命定义的，本身是一个随机变量。若定义叶片剩余寿命分布(Distribution of Remaining Life, DRL)为

(;)=(<≤+|>,())>0

(35)

则第台发动机基于内的历史协变量过程()=()的条件下，经过飞行循环的剩余寿命分布可表示为

(;)=((<≤+|>,

(),(,+)))

(36)

式中：(,)=(():<<)是～飞行循环内叶片的协变量历史；是关于(,+)|()=()的条件期望。而基于当前的历史协变信息预测未来的协变过程十分复杂，且直接得到剩余寿命分布的数学表达式较为困难。对于一台服役状态下的某机队的民用航空发动机而言，一旦投入到航线开始运行，通常需要重复执行相同的航班任务，其历史飞行航线结构就相对较为固定，因此可以从历史航班和对应的协变量信息中抽取样本，作为未来飞行航班信息的预测，从而使用蒙特卡洛数值仿真的方法，对剩余寿命分布进行评估。蒙特卡洛仿真流程如下：

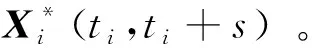
2) 得到更新的协变量历史数据：

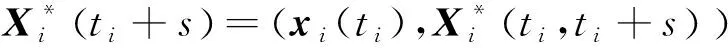
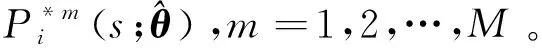
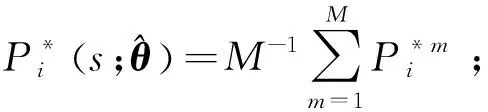
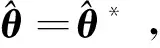
7)重复过程6)次，得到：

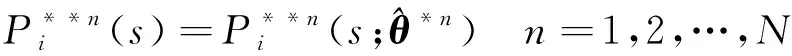
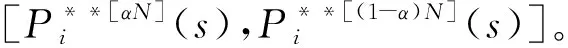
4 仿真验证

要验证提出方法的有效性，不仅需要叶片的寿命统计数据，还需要对应的发动机工况监测数据，目前收集的外场样本数据有限，在某机队航班历史数据基础上，采用第2节所述涡轮叶片蠕变寿命仿真方法，通过仿真获取涡轮叶片的寿命数据样本及其历史航班的动态协变量数据，验证提出的模型与方法。

4.1 涡轮叶片蠕变寿命周期仿真

收集的某机队的历史飞行数据涵盖了1～12月的航班数据，设计转速为14 600 r/min，其中一个航班的和历程，如图10所示。

图11为涡轮叶片蠕变寿命周期仿真流程，其中FN=1,2,…,100为发动机编号。在满足飞机起飞安全性的前提下，以相对于发动机正常起飞推力较小的推力起飞的方式叫做减推力起飞，也称灵活推力起飞。现代高涵道比民航发动机一般具有较高的推力储备，因此采用减推力起飞不仅完全可行，这种起飞方式不仅能够延长发动机的使用寿命，还能够节省燃油，降低运行成本。因

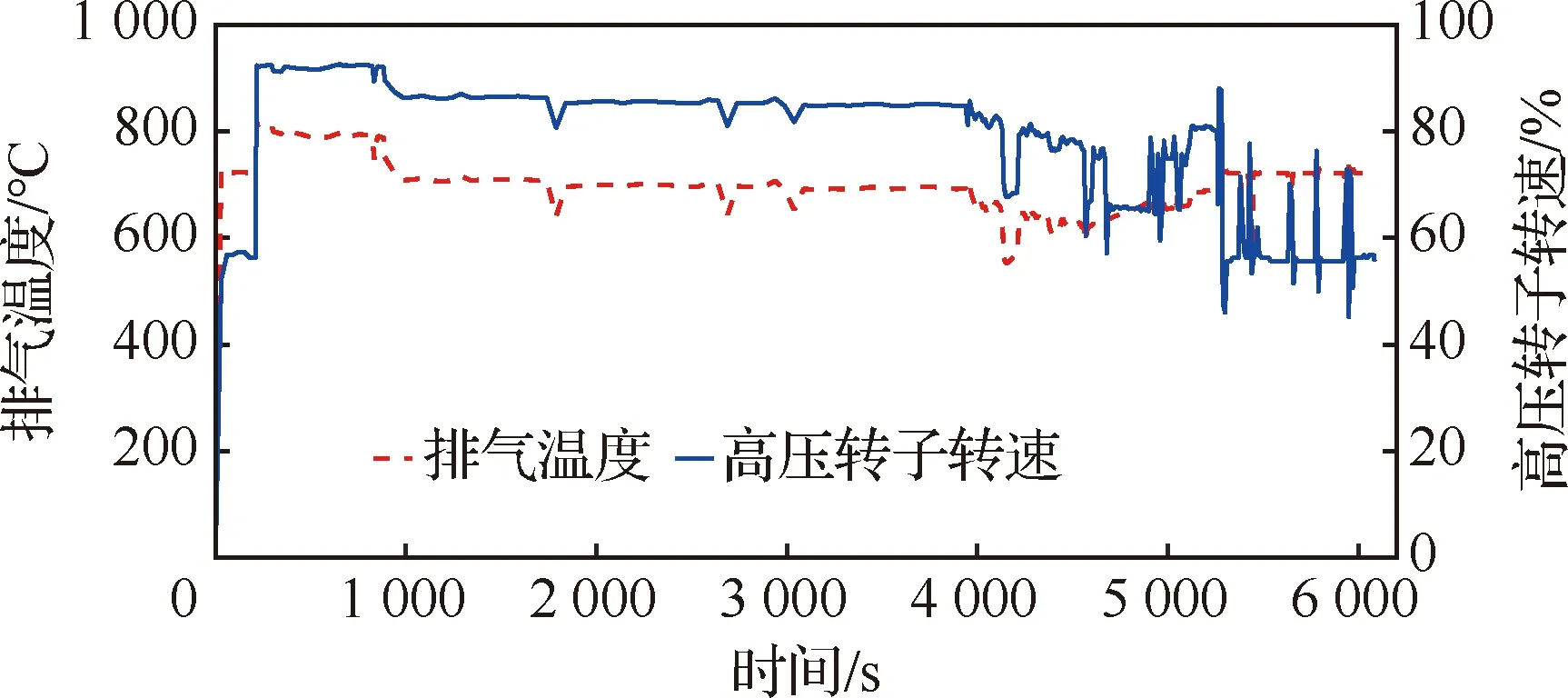
图10 排气温度和高压转子转速历程Fig.10 Course of exhaust temperature and high pressure rotor speed history

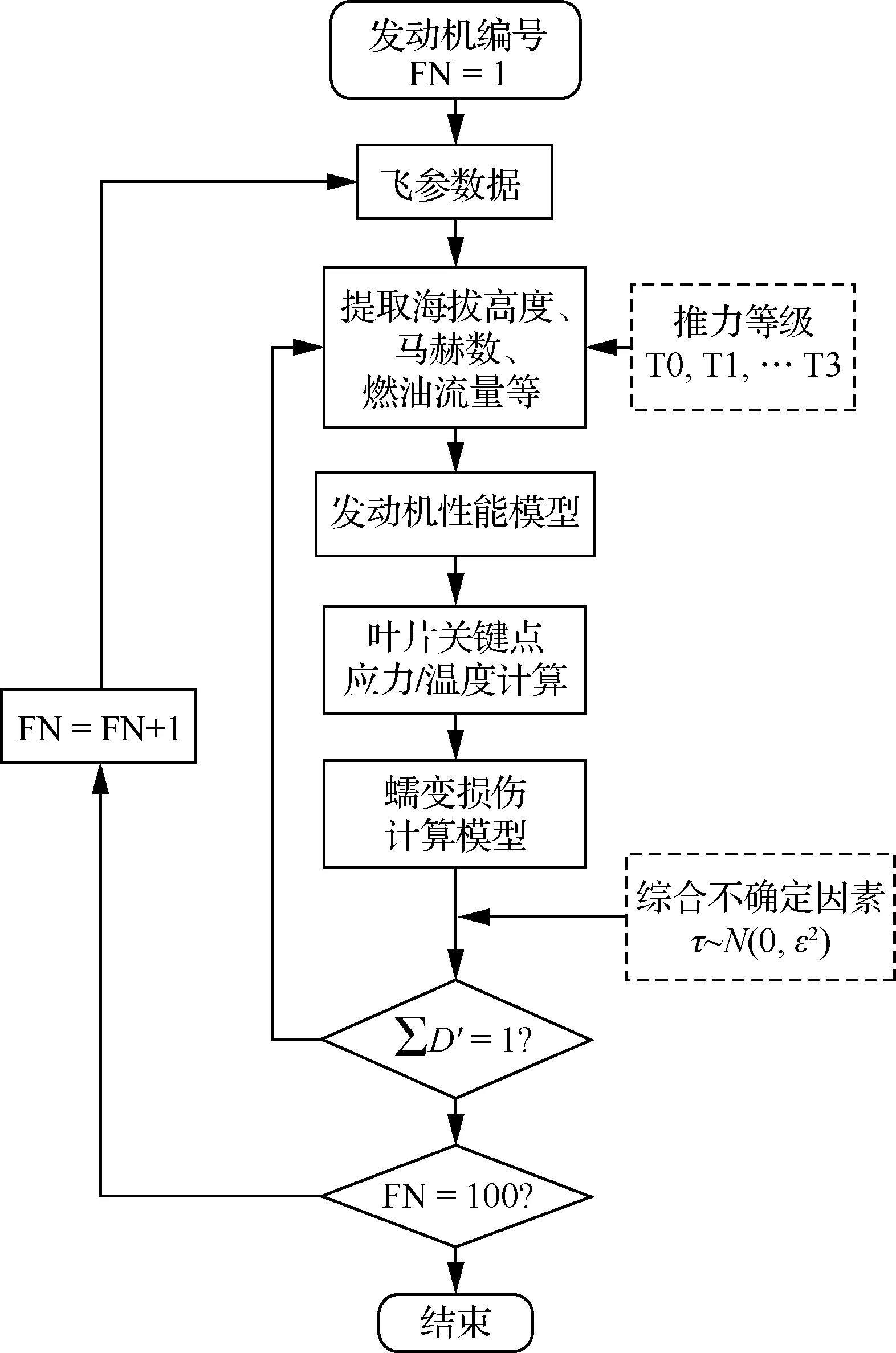
图11 蠕变寿命周期仿真Fig.11 Creep life cycle simulation

此考虑到飞机的减推力起飞，在进行仿真时将发动机的额定推力等级考虑在内，对历史航班按照4个推力等级划分，其燃油流量分别为满推力的100%、97%、94%和91%，分别对应T0,T1,T2,T3起飞阶段减推力的4个等级；同时考虑到寿命评估的不确定因素，可将不确定性来源总体上划分为三类：一是叶片设计阶段的材料参数分布、计算机辅助设计误差等引起的不确定性；二是叶片制造阶段的材料晶体缺陷、验收测量精度等引起的不确定性；三是叶片使用阶段的自然环境载荷、发动机性能退化等引起的不确定性。这些不确定性相互作用，最终导致了服役叶片的实际可用时间与设计时间不符。考虑到以上不确定性来源的影响，使用一个随机变量～(0,)代表这些因素的综合作用，其中为随机变量方差，由于随机变量的均值影响的是全寿命样本整体飞行循环的偏移，这种数据偏移的影响理论上可以通过分布的标准化过程进行消除，因此为了方便后续处理和分析，随机变量的均值取为0。寿命周期仿真时，每次从相应的样本空间随机抽取航班，记录下飞参数据和计算得到的蠕变损伤，则不确定性因素影响下的航班损伤为′=(1+)，将′作为此次抽取的实际损伤进行累积，当损伤累积到1时停止抽样，每进行1次这样的抽样循环便得到了一台发动机的全寿命样本，按照上述方法，每个推力等级下各仿真25台全寿命样本,4个推力等级共包含100个全寿命样本，对应的寿命分布如图12所示。

其中1台发动机全寿命周期的蠕变损伤量分布，如图13所示，可以看到发动机的单个航班蠕变损伤量大约分布于10～10之间，同一台发动机不同航班的蠕变损伤呈现较强的分散性，损伤量差距高达10倍，这主要是不同航班的运行载荷不同导致的结果。

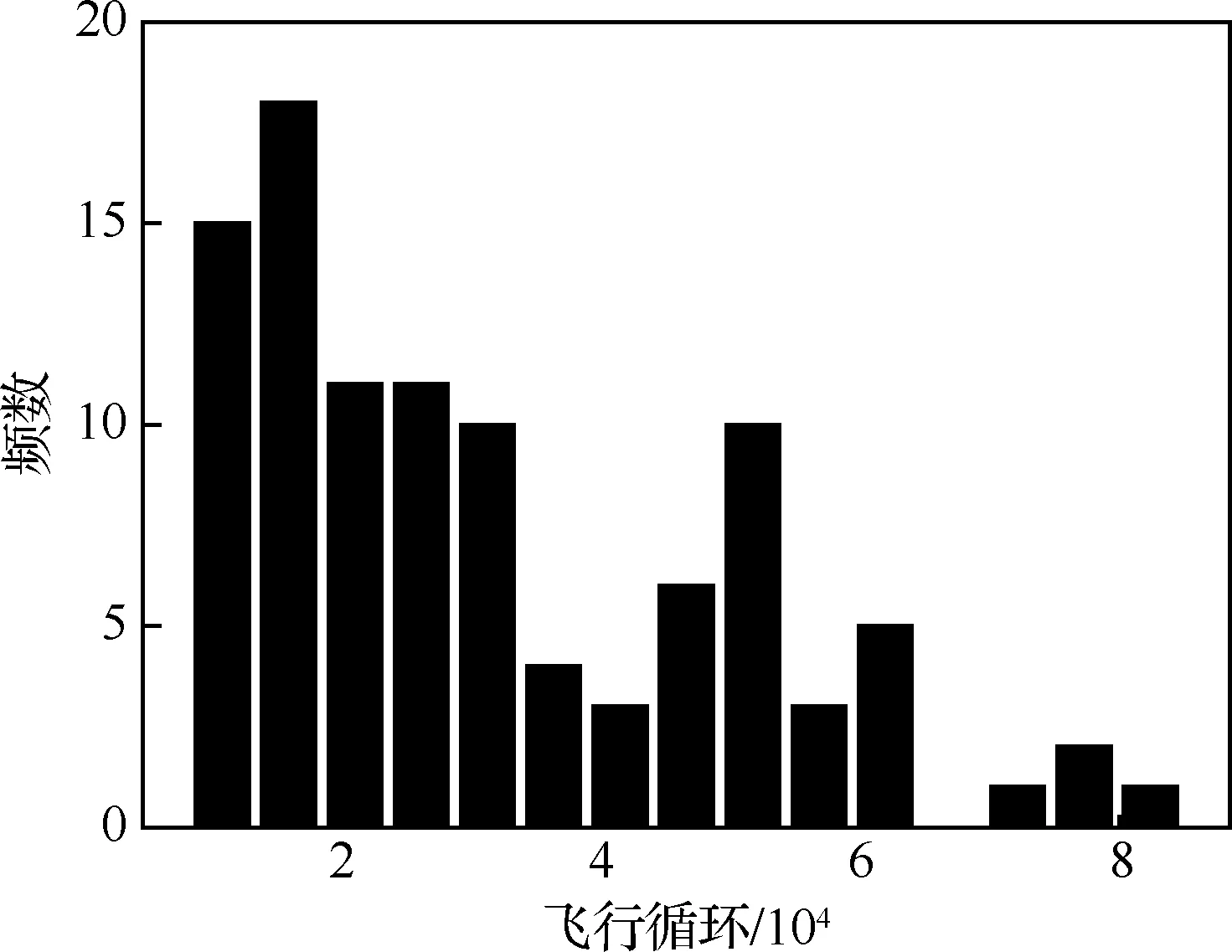
图12 HPT叶片寿命分布直方图Fig.12 Distribution histogram of HPT blade lifetime

取其中一个高损伤与一个低损伤航班，并分别统计起飞爬升阶段的数据，从图14和图15中可以看出，蠕变损伤较大的航班对应的相对排气温度和相对高压转子转速水平普遍高于蠕变损伤较小的航班，说明服役条件下的载荷水平差异是引起不同航班蠕变损伤差异性的重要因素。

分别统计1台发动机主要飞行阶段的累积损伤以及相应的持续时间占比，统计结果如图16所示。5阶段为飞机爬升阶段，叶片处于高负载状态，此阶段持续时间所占比重较小，约为总时间的12.5%左右，但累积蠕变损伤却占总损伤的80%以上；6阶段为飞机巡航阶段，叶片处于低负载状态，此阶段的时间占比达到了50%以上，但累积损伤占总损伤不到10%，说明叶片在高温和高应力水平下的单位时间蠕变损伤效应已经超过了飞行历程内蠕变损伤的时间累积效应。

图13 航班蠕变损伤统计情况Fig.13 Statistics of flight creep damage

图14 起飞爬升阶段相对排气温度历程Fig.14 Relative exhaust temperature course during takeoff and climb phase

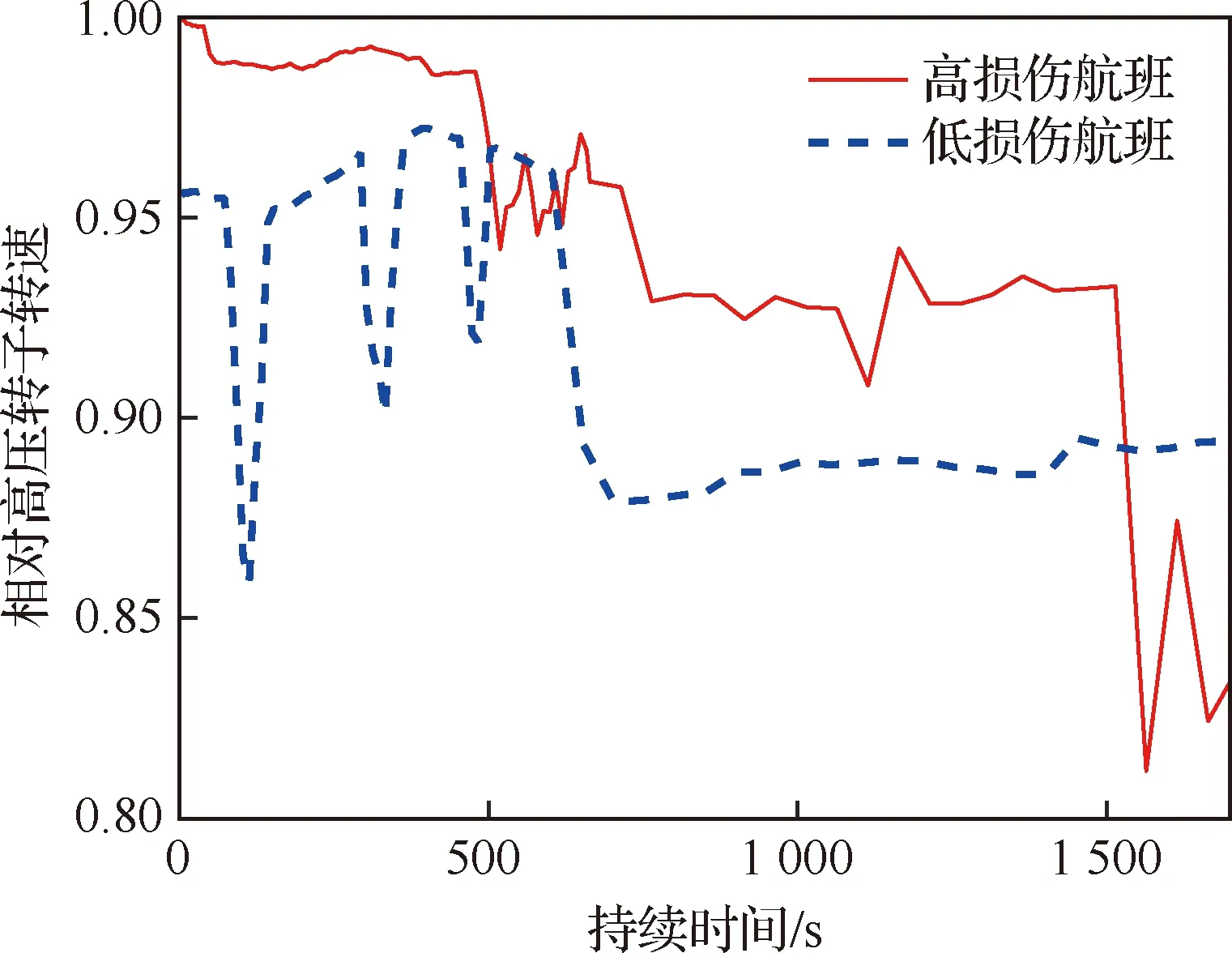
图15 起飞爬升阶段相对高压转子转速历程Fig.15 Relative high pressure rotor speed course during takeoff and climb phase

图16 飞行阶段损伤统计Fig.16 Damage statistics during flight phase

4.2 基于蠕变累积损伤指数的可靠性寿命评估

仿真得到的100台发动机样本中，随机抽取50台作为失效样本，这部分发动机保留寿命周期的飞行航班数据和对应的动态协变量信息，失效标志位记为=1(=1,2,…,50)；剩余50台作为未失效样本，对飞行循环进行随机截尾处理，记录截尾时刻之前的航班及对应的协变量信息，失效标志位记为=0(=51,52,…,100)，以此模拟机队发动机叶片实际使用寿命的统计情况，其中前20台发动机截尾数据分布如图17所示。

图17 发动机截尾数据Fig.17 Censored engine data

使用R语言编写似然函数，并调用optim优化函数进行估计参数的迭代求解，其中，优化方法设置为BFGS，BFGS方法属于Quasi-Newton方法，其在最优值附近的计算收敛速度快，迭代次数少。经过546次迭代计算，得到式(28)中的参数估计值：

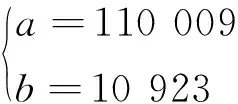
将、反代可以求出每个航班的累积损伤指数。将每台发动机所有航班累积损伤指数累加，即可得到每台发动机截尾时刻对应的总损伤指数，计算结果的统计情况如图18和图19所示。

由图18和图19可见：① 失效样本的累积损伤指数普遍大于未失效样本的累积损伤指数，且两种损伤指数分界较为明显，可以很好地区分失效样本和未失效样本，说明本文定义的蠕变累积损伤指数可以很好的表征HPT叶片的实际损伤状态。② 蠕变累积损伤指数与飞行循环数没有明显的强相关性，仅仅借助飞行循环数或飞行时

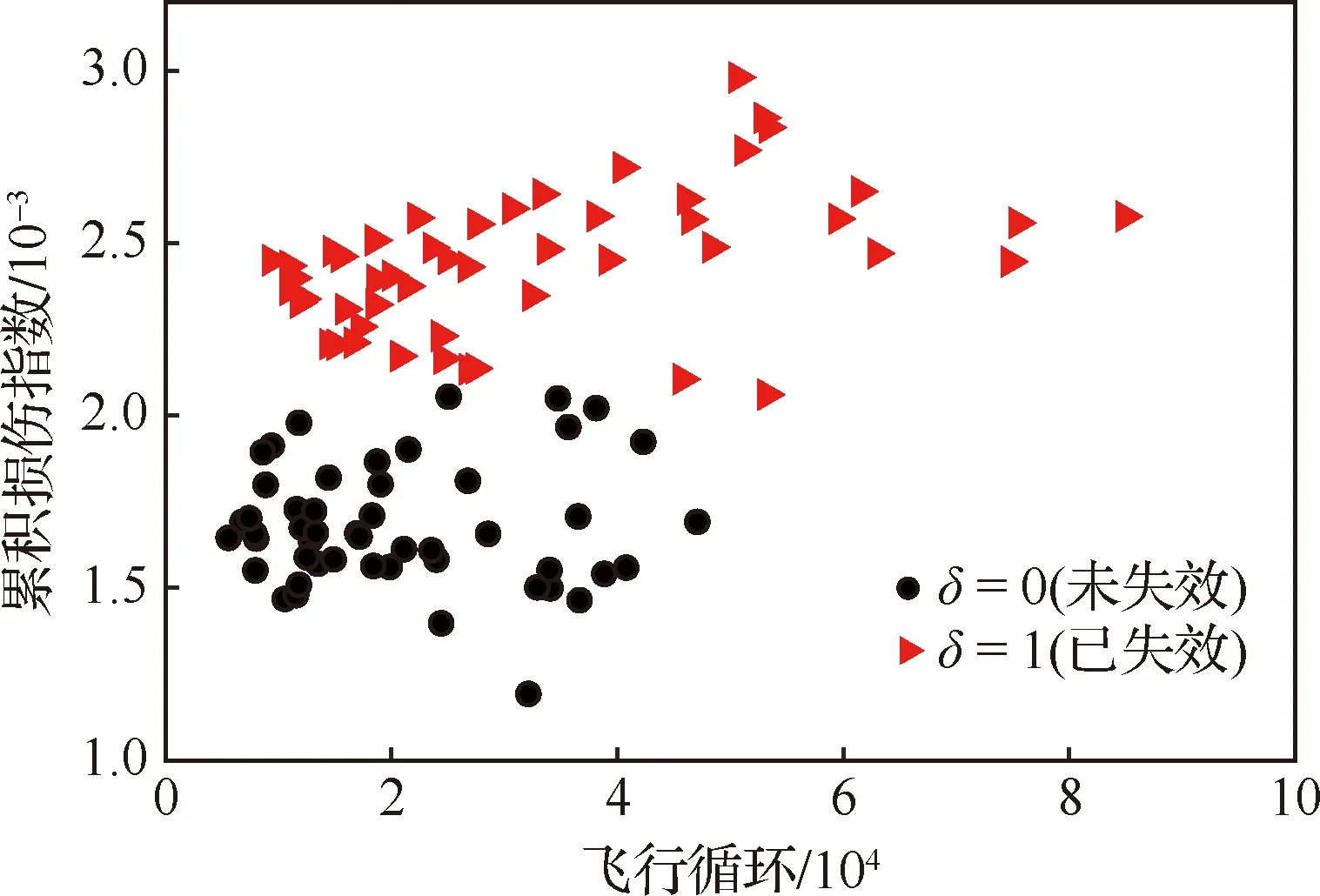
图18 蠕变累积损伤指数散点图Fig.18 Scatter plot of creep cumulative damage index

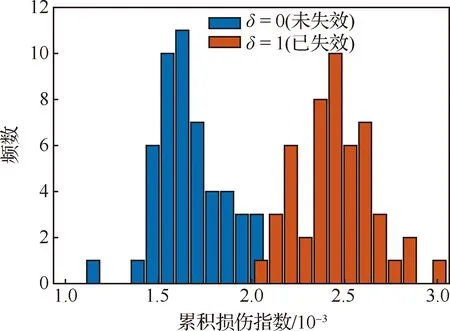
图19 蠕变累积损伤指数直方图Fig.19 Histogram of creep cumulative damage index

间来表征HPT叶片的累积损伤并不合适，低飞行循环数累积损伤指数可能较大，叶片已经发生蠕变失效，而高飞行循环数累积损伤指数可能较小，叶片仍可以正常服役。这是因为HPT叶片蠕变累积损伤的不仅仅取决于飞行时间，还取决于经历的温度、应力等环境载荷参数。③ 失效样本的累积损伤指数呈一定的分散性，失效阈值并不是一个确定值，这是因为即使同一型号的HPT叶片，不同个体在“设计—制造—使用”中不可避免地引进不确定性，这些不确定性的相互作用正是导致服役条件下失效叶片累积损伤指数发散的重要原因。

式(30)中的估计参数值和95%置信区间边界值见表4，其中为极值分布的均值，ln()为极值分布标准差以e为底数的对数值。从而得到基于累积损伤指数的失效概率图(图20)，可以看到，累积损伤指数基本符合威布尔分布。

对50个未失效样本的未来协变过程进行蒙特卡洛仿真，仿真设置为步长=80 000，单轮仿真次数=1 000，仿真轮次=100。仿真计算得到的其中四台发动机叶片剩余寿命可靠性分布如图21所示。

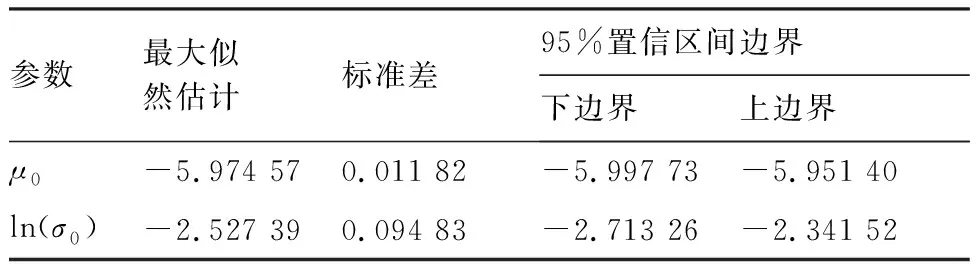
表4 蠕变寿命计算结果Table 4 Creep life calculation results

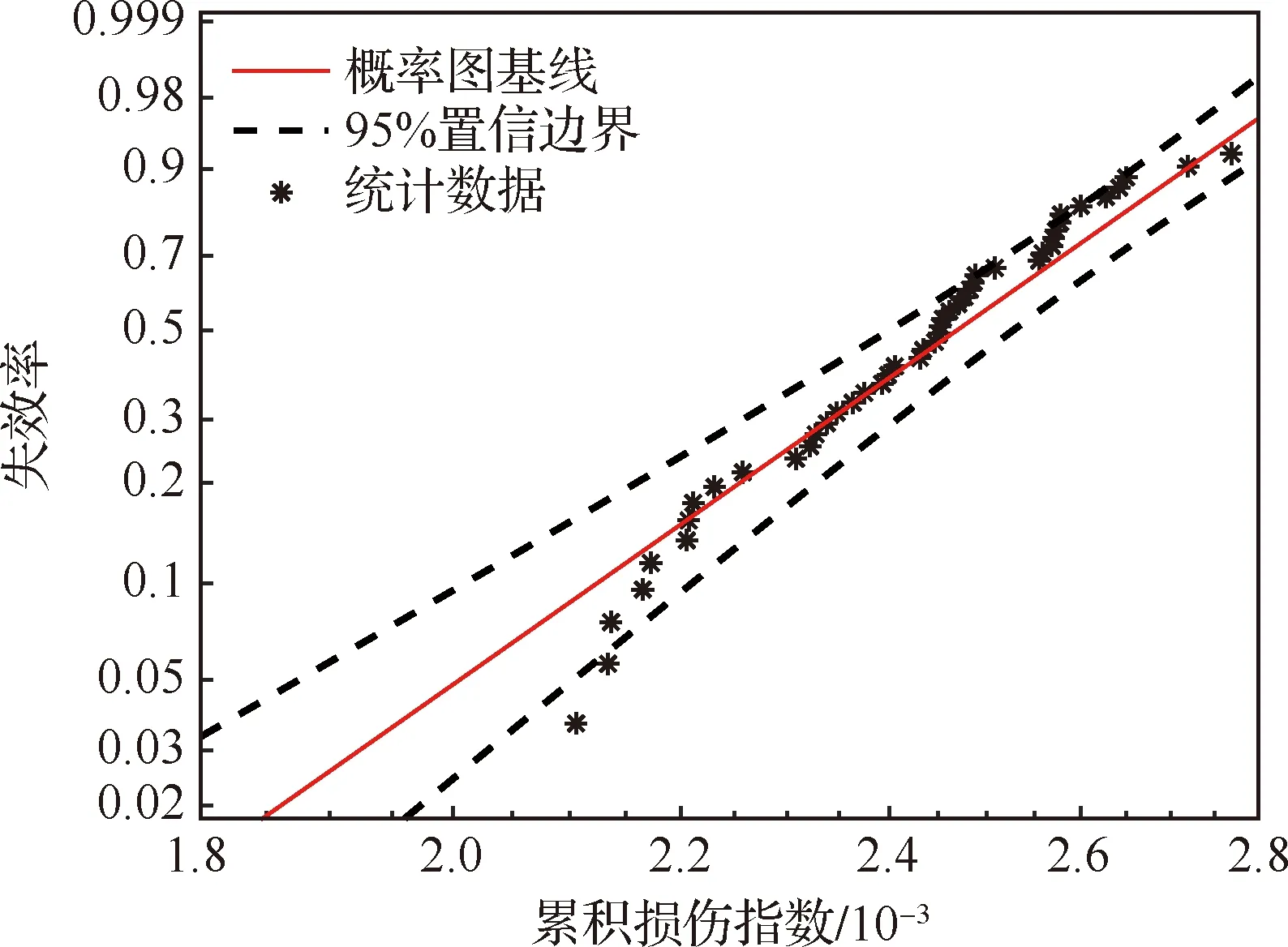
图20 随累积损伤指数变化的失效概率图Fig.20 Diagram of failure probability changing with cumulative damage index

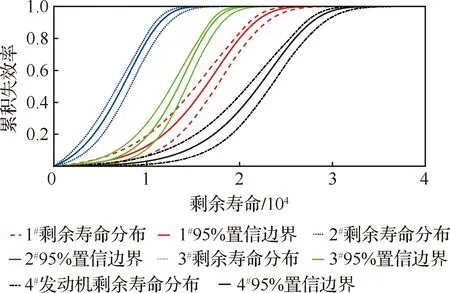
图21 剩余寿命可靠性分布Fig.21 Distribution of remaining life reliability

上述分布表示了从统计截止时间起，未来叶片累积失效率随飞行循环数的变化过程。由于协变量历史信息的不同，图中四台发动机剩余寿命可靠性分布具有明显差异，这也体现了实际服役条件下叶片的个体差异性。针对剩余寿命分布，工程上常用式(37)所示的平均剩余寿命(Mean Residual Life, MRL)作为剩余寿命预测值。

(37)

式中：()为可靠度函数；为当前截止时间。

在得到了叶片的寿命分布函数的估计参数后，可以根据分布类型推导出对应的可靠度分布函数，之后代入式(37)中即可计算出与分布对应的平均剩余寿命。一般情况下通过直接统计截尾数据的方式也可以得到使用寿命的分布函数。把这种传统的处理方法记为基准模型，分别使用本文定义的累积损伤指数模型与基准模型按照式(37) 进行平均剩余寿命计算，部分结果如表5所示，其中使用寿命指的是截止时间的实际使用寿命，剩余寿命是在已知全寿命的基础上去除使用寿命后剩余的飞行循环数，这两部分数据对应着全寿命仿真中模拟的未失效样本。其中30台发动机的预测偏差如图22所示。

结合表5与图22中的预测结果可以看出，基于失效时间分布的剩余寿命预测偏差大约在-30%～1 200%的范围内，说明预测误差具有较大的分散性，基本不具备参考价值；使用累积损伤指数进行的预测偏差大约在-20%～20%之间分

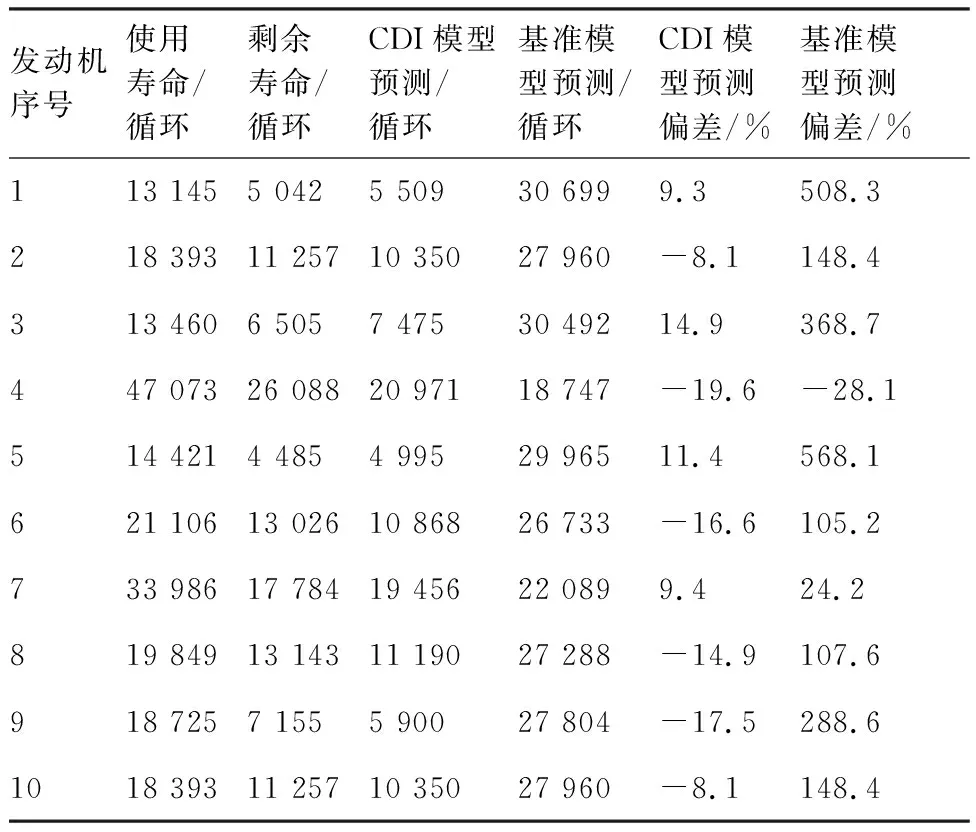
表5 平均剩余寿命预测结果对比Table 5 Comparison of MRL prediction results

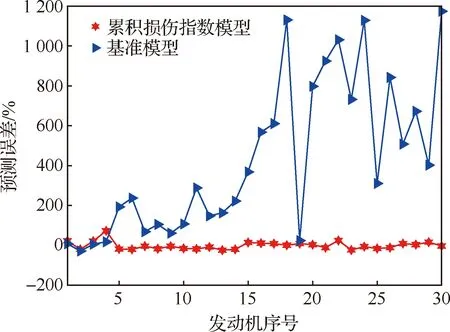
图22 预测结果偏差Fig.22 Forecast result deviation

布，说明预测误差分散性小，结果总体在可接受范围内，可作为维修计划定制的参考剩余寿命。

5 结论及展望

1) 针对民航发动机涡轮叶片的剩余寿命预测，提出了一种数据驱动与失效物理融合的可靠性剩余寿命预测方法，基于服役条件下的历史工况监测数据，结合发动机性能仿真模型、叶片应力和温度计算模型对叶片表面参考点的温度和应力历程进行计算；在此基础上使用拉森米勒参数法对叶片蠕变损伤进行评估；之后针对蠕变损伤定义了一种累积损伤指数模型，融合历史协变量信息排气温度和高压转子转速对叶片剩余寿命进行了可靠性评估，并通过数据仿真分析验证了本文建立模型的可行性，为涡轮叶片可靠性评估提供了一种新的思路。

2) 针对服役条件下的HPT叶片蠕变寿命预测，使用本文的模型方法得到的预测结果，预测偏差大约在±20%范围内分布，而传统的基于失效时间分布的可靠性分析方法，得到的预测偏差约在-30%～1 200%之间，说明提出的模型具有更好的适用性，在寿命预测精度上也更具有优势。

3) 反映发动机关键件服役可靠性降级等行为特性的信息存在于多模态数据中，包括产品设计数据与使用维护数据，如产品几何参数、材料数据、状态监测数据、离线检测/检查报告、故障记录和大修报告等，贯穿产品寿命周期的不同阶段，如何充分利用这些多模态数据，实现多领域物理模型与数据融合，是提高服役发动机关键件寿命预测分析准确性的重要途径。以民航发动机HPT叶片蠕变失效为例，在蠕变失效机理分析基础上，同时考虑服役条件下的使用信息、状态参数及截尾失效时间等数据，提出的蠕变累积损伤指数模型实现了多模态信息的融合，对涡轮叶片服役可靠性进行评估，并预测其剩余寿命。

4) 本文中涉及的叶片损伤正向计算中，每个计算环节都会不可避免地引进计算的不确定性，这些不确定性既有认知的不确定性，也有材料、设计等固有的不确定性，这是正向计算所不可避免的。因此“数据驱动与失效物理融合”是对可靠性寿命评估方面创新性的思考，它主要体现在累积损伤指数模型的建立过程以及外场使用数据、截尾寿命数据的融合过程中。损伤指数定义的方式基于一系列的正向的计算基础上的推导，而发动机性能模型、温度计算模型、应力计算模型和失效模式对应的损伤计算物理模型都与失效物理相对应；之后通过分析蠕变失效机理以及物理模型，推导了一种新的蠕变损伤累积指数模型，在此初始模型的基础上进一步建立似然函数，融合外场使用数据、截尾寿命数据来估计模型参数，从而实现了在失效物理机理基础上对外场数据的融合。模型直接用到的是飞行监测数据与外场失效时间数据，而由于累积损伤模型基于失效模式定义，因此预测结果在物理层面的解释性更好。

现阶段外场数据获取有限，因此通过仿真数据验证了提出方法的可行性和有效性。下一步的工作将基于目前的研究继续深入，从以下几个方面开展：一是从热机械疲劳、高温氧化等其他失效机理入手建立对应的累积损伤指数模型，验证本文方法的通用性和鲁棒性；二是研究有效的动态协变量预测方法，来代替目前使用的蒙特卡洛仿真过程，以取得更好的参数估计结果和预测精度；三是跟踪预测部件的实时状态，对本文的模型方法进行实际数据的验证。