随机激励作用下飞机飞行姿态动力学研究
李海泉,陈小前,张嘉图,王亮
1. 国防科技大学 航天科学与工程学院,长沙 410073 2. 中国航空工业集团有限公司 沈阳飞机设计研究所,沈阳 110035 3. 中国人民解放军军事科学院 国防科技创新研究院,北京 100071 4. 西北工业大学 数学与统计学院,西安 710072
进入21世纪以来,中国的航空科技事业面临着巨大的发展机遇与挑战。新一代飞机设计对平台性能和作战效能要求越来越苛刻,总体综合优化问题越来越突出,飞行控制系统精细化设计要求不断提高,这都对飞行动力学模型的精准度提出了更高的要求。加强对飞行动力学建模和求解方法的研究,不仅影响着飞机飞行仿真系统的运行效率和精度,也对提高设计质量、确保飞行安全具有重要的意义。
目前的飞行器设计方法一般仅考虑确定性情况下的建模仿真,忽略了实际上广泛存在的各类不确定性影响,如复杂的外界飞行环境干扰、飞机本体零部件质量以及加工、装配质量等都可能存在不确定性。飞机在飞行过程中,由于飞机本体具有复杂的结构和测量控制系统,飞行环境中温度、湿度、气流运动等因素复杂多变,完全基于确定理论来建立飞机的飞行动力学模型无法模拟飞机的真实飞行状态,在型号实践中常遇到飞行动力学仿真结果与飞行实际测量数据存在较大偏差的现象。飞行动力学模型是研究飞机控制、性能、操稳、载荷等问题的基础,由于仿真结果的精度问题,通常为了保证设计结果的可靠性,不得不在仿真数据上乘以固定的安全系数,这样做付出了巨大的代价。
随机噪声广泛存在于实际问题当中,对真实的系统具有重要的影响,这些不确定性从数学的角度可以描述为各种各样的随机噪声和随机变量。学者们往往通过在确定仿真系统中恰当地引入随机因素,来展示一个更加准确的客观世界,从而更好地探索问题本质。研究人员为了获取准确的飞行仿真结果,通过引入大气扰动等随机模型来模拟连续紊流、阵风等飞行过程中的随机因素,研究飞行动力学响应特性。这些研究中的随机模型多是根据假设建模或来源于大气观测,或来源于结构、气动单一学科的因素,目前还没有采用飞行实测数据进行随机模型的建模研究,而飞行实测数据往往包含较全面的不确定因素。随着系统及参数识别理论的不断完善,以及飞机飞行实验积累了大量飞行实测数据,基于实测飞行参数统计分析来建立并修正飞行动力学模型,可以为更准确地研究飞机飞行动力学问题提供强有力的支撑。
本文基于飞行实测数据,合理引入随机因素建立不确定性模型,通过与确定性模型和实际情况的对比,分析姿态响应的差别程度,探索这些随机因素的概率统计特性,研究其对确定模型的影响,对于认识一个更加准确的飞机飞行动力学问题具有重要的意义和作用。
1 通用飞行姿态动力学模型
飞机姿态动力学方程是描述飞机飞行状态的一类基本的力学方程,这些方程描述了飞机在飞行过程中在各个方向的速度、角速度及加速度。一般来说,姿态动力学方程描述如式(1)~式(3)所示。
力方程

(1)
力矩方程

(2)
其中:

(3)
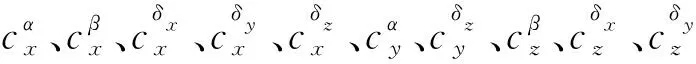
另外,机体坐标系下的飞行运动学特征由式(4) 和式(5)描述。
姿态角方程
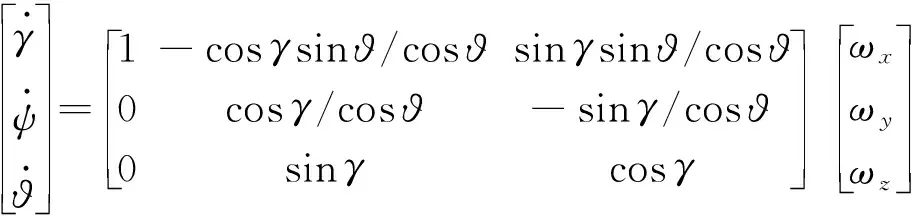
(4)
质心运动方程
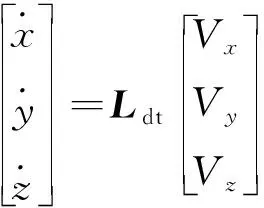
(5)
其中:

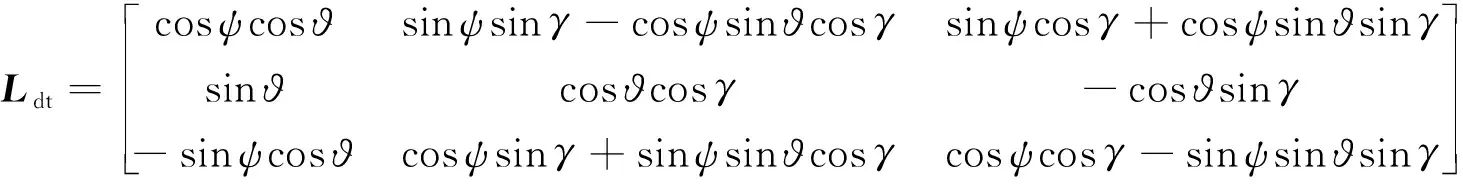
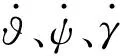
式(1)~式(5)都是在理想状况下建立的,在实际飞行过程中,飞机可能会受到诸多因素的影响,譬如气压、气温、大气密度、湍流等,以及飞行过程中受到的载荷、复杂外界环境的干扰、飞机本体参数的不确定性等等。这些因素是物理系统及其环境中的固有可变性,都可能造成求解方程所得到的结果与真实数据产生偏差。为了使飞行运动学方程的求解结果更加符合实际情况,本文将考虑上述主要因素对方程的影响,即在一些对外界或本体因素敏感的飞行参数或变量中合理引入随机噪声或随机变量,然后再对新得到的飞行运动学方程在随机动力学理论框架下进行求解。
2 具有随机不确定性激励的飞机飞行姿态动力学模型
当多种复杂的随机因素共同作用在飞机上时,飞机受到的力和力矩就会发生随机的变化,飞机的动力学现象就会表现出不确定性,这会影响飞机的速度、姿态等动力学参数。因此,合理的分析飞机产生噪声的机理,准确的将随机因素引入到飞机动力学模型中进行计算,对飞机动力学特征的描述就会更加准确。通常,飞机在飞行过程中需要通过控制舵面的偏转来改变飞机姿态,其中飞机所受到的气动力矩是改变飞机姿态最为主要的因素。本文以式(2)为例,研究随机因素对于飞行姿态动力学的影响。
通过大量飞行实测数据的统计分析之后,可以粗略估计这种随机现象的特定属性。首先对飞行实测数据进行预处理,即在主要的处理以前对数据进行的一些处理,例如将数据中的某些异常值除去,之后对处理过后的数据进行核密度估计,即采用平滑的峰值函数(“核”)来拟合观察到的数据点,从而对真实的概率分布曲线进行模拟。之后将其与确定性结果进行对比分析,从而可以根据它们的统计学特征,例如某些情况下,这种随机因素往往是具有周期性的,并有较为稳定的频率,但是并不严格按照某个周期运动。某些情况下,这种随机因素的幅度分布可以近似为高斯分布。因而这种随机现象可以用随机相位激励或者高斯白噪声来描述。
本文重点研究随机相位激励和高斯白噪声对飞机姿态动力学的影响。假设姿态动力学方程的随机作用主要体现在力矩项,将随机噪声引入式(2) 力矩项得到式(6)。

(6)
式中:()、()、()为随机激励或随机噪声。在对该模型进行分析求解时,发现由于式(3)力矩项中、、等操作参数会随着时间变化而变化,因此该系统为一变参数系统。对于变参数系统,使用传统的数值方法很难对其进行求解,文献[19]中采用了3种传统摄动方法对其分析求解。针对本文涉及到的变参数系统,本文对传统的数值方法进行改进同时采用蒙特卡洛模拟法对式(6) 进行求解,进而分析随机因素对于该系统的影响。
首先,使用蒙特卡洛模拟法,采取与文献[20]中类似的做法对方程进行分析求解。蒙特卡洛模拟法指的通过大量产生随机数的模拟方法来用于数值统计计算以获得问题的近似解,其数学基础是概率论中的大数定理,即频率依概率收敛于概率。蒙特卡洛方法能够比较逼真地描述事物的特点及物理实验过程,解决一些数值方法难以解决的问题。在具体操作过程中,只要样本取得足够多,可以得到任意精度的结果。在考虑加入随机噪声或是随机激励后的随机微分方程组,可以借助蒙特卡洛模拟法的思想,利用数值方法和蒙特卡洛模拟法对所得到的随机微分方程组进行求解。
另外,由于随机系统的响应是一个随机过程(或者是一随机变量),无法与真实数据直接进行对比,故此时考虑通过提取随机响应的数字特征,即样本均值,通过比较样本均值响应与确定性响应和实际数据的异同,来说明随机的影响以及随机系统是否能够更好的描述实际飞行问题。
下面通过两型飞机具体数值仿真来说明随机因素对式(2)的影响。
3 数值仿真
3.1 确定模型与随机模型仿真结果对比
首先以某大型运输飞机为例,其部分参数如表1所示。
根据表1数据,设飞机以=204 m/s的飞行速度进行压坡度转弯机动飞行。对确定性模型式(2)以及受到随机扰动的模型式(6)进行分析,基于一些飞行实测数据和经验认识,发现某些随机扰动往往是具有周期性的,并有较为稳定的频率,但是并不严格按照某个周期运动,而随机相位激励表示的是一种具有周期性的噪声激励。因而可以取式(6)中()、()、()为随机相位激励,随机相位激励表达形式为:()=cos(+),=1,2,3。其中为位移幅值;为响应频率;Φ为随机相位角。根据经验以及对于一些飞行实测数据的分析,取=0000 3、=0003、=0000 03,=1,为噪声强度为0.01的高斯白噪声。
计算得到的结果如图1~图3所示,其中红线代表确定性模型式(2)的计算结果。由于随机动力学模型式(6)的计算结果是一个随机过程,也就是随机变量的集合,因此无法画出其轨迹,上图的蓝线画出了其均值响应。通过对比图1~图3,可以直观的观察到,在随机相位激励的作用下,均值响应与确定性姿态动力学方程的轨迹不同。当飞机进行主动机动时,随机因素的影响并不明显,但对机动制动过程有特别显著的影响,这说明随机因素对于飞机的动力学行为有一定的影响,具体的影响将在3.2节进行描述。

表1 某型号飞机部分参数Table 1 Some parameters of a certain type of aircraft
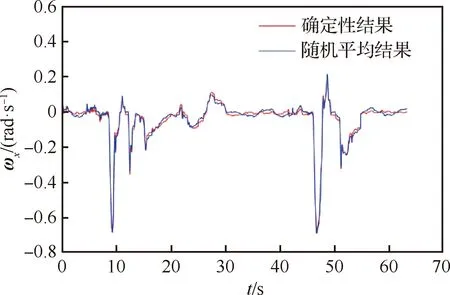
图1 ωx求解结果对比Fig.1 Comparison of solution results of ωx
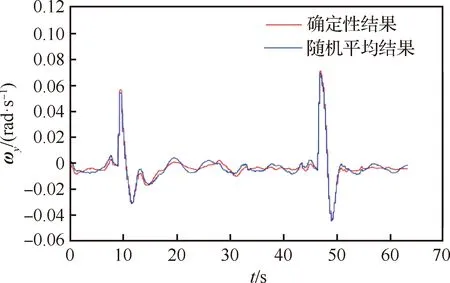
图2 ωy求解结果对比Fig.2 Comparison of solution results of ωy

图3 ωz求解结果对比Fig.3 Comparison of solution results of ωz
3.2 确定性与随机性关于飞行实测数据的比较
本节将通过一组飞行实测数据来对比分析随机因素对确定性仿真模型所带来的影响,表2为一型高机动飞机的典型参数。
根据表2数据,设飞机以=204 m/s的飞行速度飞行。
1) 飞行状态1
在飞行员有较大操纵时的飞行状态下,基于飞行实测数据,取式(6)中()为均值是零、噪声强度是0.01的高斯白噪声。确定性模型式(2)以及受到随机因素影响的模型式(6)的计算结果如图4和图5所示。
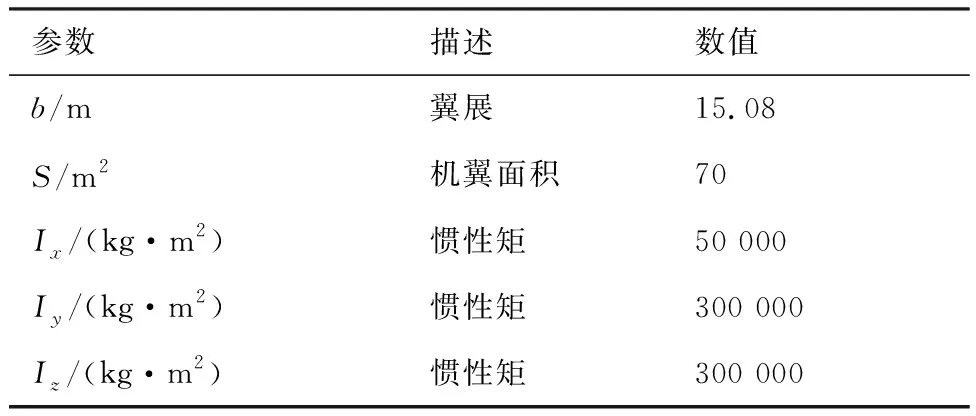
表2 高机动飞机的部分参数Table 2 Some parameters of high mobility aircraft
图4和图5分别为角速度分量、的计算结果。其中红线代表通过确定性模型式(2)求解所得到的确定性轨线;蓝线代表高斯白噪声下的姿态动力学模型式(6)的均值响应;黑线代表的是飞机飞行过程中的飞行实测数据。从图4、图5可以发现,飞机在急剧滚转情况下,确定性模型和随机模型仿真结果非常接近,由于操纵力远大于随机因素,不确定性因素影响不显著;在角速度快

图4 ωx求解结果对比(状态1)Fig.4 Comparison of solution results of ωx (Case 1)

图5 ωy求解结果对比(状态1)Fig.5 Comparison of solution results of ωy (Case 1)
速变小的急剧制动过程中,飞机主动机动减弱过程中不确定性因素影响较大,并且随机模型仿真结果与飞行实测数据非常接近(图4中圆圈所示)。经过本状态分析可见受高斯白噪声作用的姿态动力学模型在一定程度上更能体现姿态动力学的特征。
为了更好地描述随机因素带来的影响,采用全历程均方差定量地来分析以上数据。表3给出了飞行状态1确定性模型及随机模型求解结果与飞行实测数据间的均方误差。
2) 飞行状态2
在飞行员操纵飞机稳定飞行状态下,同样取式(6)中()为均值是零、噪声强度是0.01的高斯白噪声,确定性模型式(2)以及受到随机因素影响的模型式(6)的计算结果如图6、图7所示,并且通过表4给出本飞行状态确定性模型及随机模型求解结果与飞行实测数据间的均方误差。
图6、图7给出了飞机在稳定飞行过程中角速度分量、的计算结果。定性分析可以发现,由于主动操纵因素影响较小,飞机姿态细微变化主要是由于环境不确定性和本体不确定性,所以随机因素影响较大。通过确定模型和随机模型仿真结果与飞行实测数据对比可见,引入适当强度随机白噪声的随机模型仿真结果非常逼近飞行实测数据,说明选取合理的噪声对改善模型仿真结果意义重大。

表3 均方误差对比(状态1)Table 3 Comparison of mean square errors (Case 1)

图6 ωx求解结果对比(状态2)Fig.6 Comparison of solution results of ωx (Case 2)
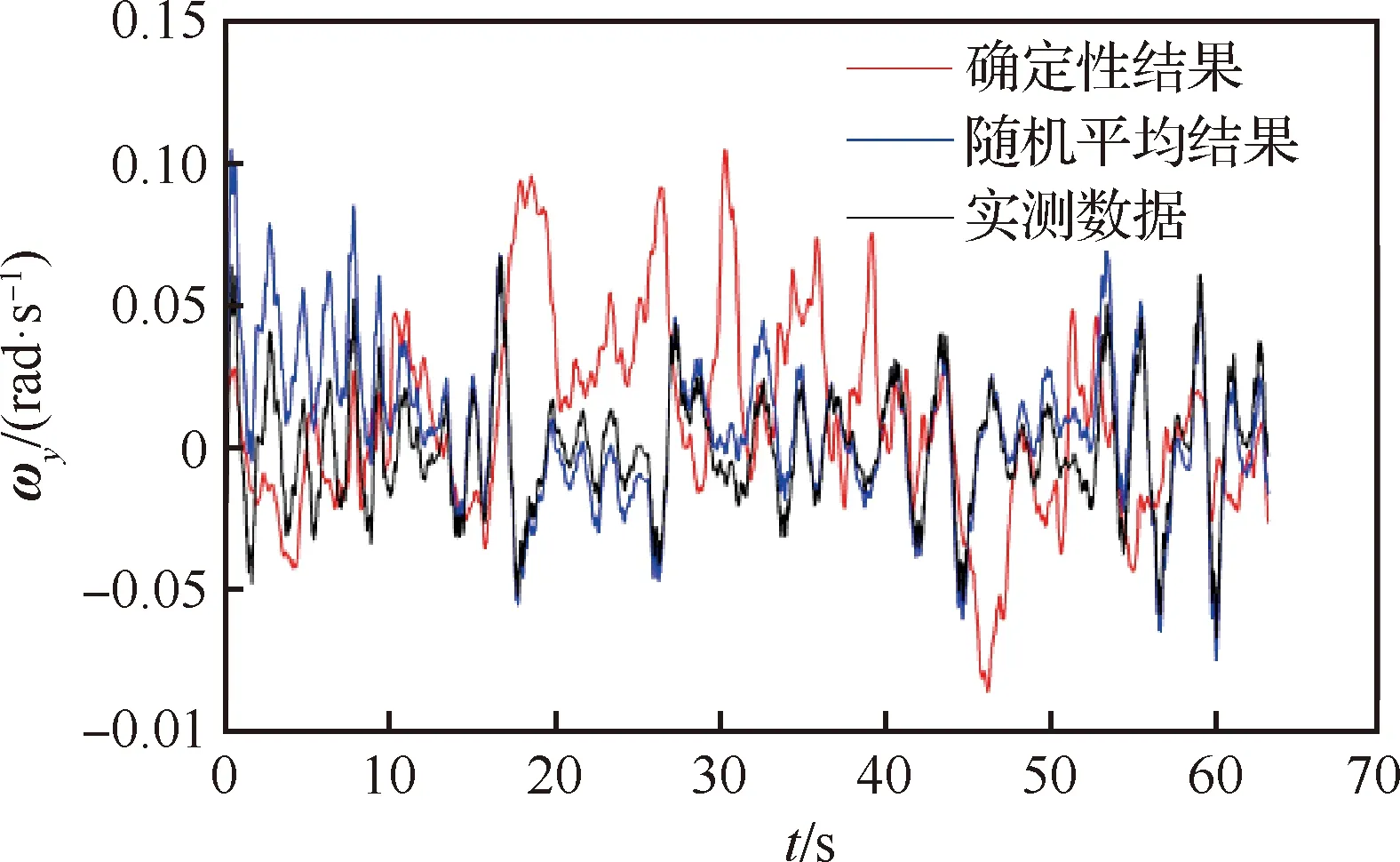
图7 ωy求解结果对比(状态2)Fig.7 Comparison of solution results of ωy (Case 2)

表4 均方误差对比(状态2)Table 4 Comparison of mean square errors (Case 2)
通过表3和表4进行初步的定量计算之后可以发现,无论是飞行员有较大操纵时还是平稳飞行状态下,考虑噪声影响的姿态动力学方程的模型一定程度上都更能贴近飞行实测数据。特别是飞机在平稳飞行过程中,随机不确定性模型更能可靠的模拟飞机的实际飞行状态。
4 结 论
通过上面所给出的计算结果,可以发现在飞机飞行姿态动力学建模仿真过程中,在仿真模型的主要参数项考虑合适的随机不确定性影响,对仿真结果有着显著的影响。
1) 从飞行仿真典型参数的时间历程曲线的定性对比和从均方误差的定量结果两方面来看,都发现加入随机噪声后的动力学方程与确定性的飞行动力学方程之间有一定差别。
2) 通过不同飞行状态的飞行姿态仿真,加入随机噪声后的动力学模型仿真结果更加贴合飞行实测数据。证实了在求解飞机动力学方程时,考虑随机噪声或者随机变量建模对提升仿真结果精度有很重要的意义。
3) 定量的验证了考虑随机因素的影响后,对大幅度机动动作影响不明显,但在飞机不进行主动机动的平稳飞行过程中,考虑随机因素可以有效提高飞行动力学模型的精度,继而可以大幅提高飞机设计参数的可信性。
目前只测试了典型的高斯白噪声对参数的影响,后续将采取参数识别的方法更好的去分析噪声的性质,寻找更合适的随机噪声或是随机激励以及在不同参数或是变量中加入随机因素的影响,不断地提高模型精度,提升飞行仿真的可信性,进而达到预期的结果。

