基于有限元法的接触网腕臂截面拓扑优化分析
李少鹏
0 引言
接触网腕臂系统广泛应用于电气化铁路牵引供电系统装备中,其零部件数量庞大,合理进行接触网腕臂结构的优化设计,可有效提高设备安全可靠性、降低工程造价成本及运营维护成本。
国内外不少工程技术人员及学者对接触网腕臂结构进行过长达数年的研究探讨,衍生出多种形式的腕臂结构,如法国的拉杆腕臂结构、日本的整体式钢腕臂以及德国的倒三角结构形式等,均各具优劣。整体上看,所有腕臂结构都遵循了“倒三角”的稳定型样式。“倒三角”结构为公认的较为合理的结构系统,但鲜有腕臂截面方面的相关研究。
本文通过对腕臂结构的截面形式进行力学分析研究,探讨接触网腕臂结构的优化形态,在保证结构可靠性的同时,尽量减小结构质量,从而降低工程建设成本和运营维护成本,并为研制中国特色的接触网系统装备提供设计思路。
1 渐进结构优化法(ESO法)
结构优化主要包含形状、尺寸和拓扑优化3种形式。形状优化将结构的形状、节点位置作为设计变量;尺寸优化将结构的外形尺寸作为设计变量;拓扑优化则通常结合有限元理论,将整体结构划分为大量的极小单元,并将这些极小单元的“有”、“无”作为设计变量,为0-1型逻辑变量[1,2]。
拓扑优化是结构优化的一种常见方式,是根据给定的边界条件、外部负载以及性能指标,在特定的区域内对单元位置分布进行优化的数学方法。拓扑优化分为连续体拓扑优化和离散结构拓扑优化,其中连续体拓扑优化主要包括变密度法、均匀化法、渐进结构优化法(ESO)等,其优化数学模型一般如下[3,4]:
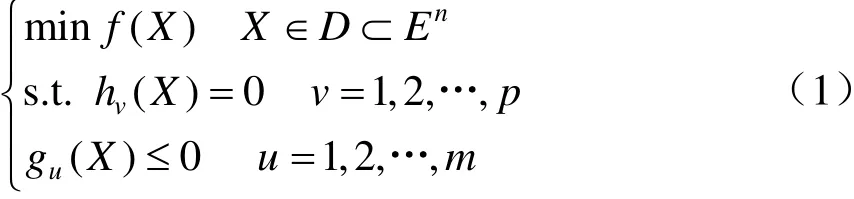
式中:X为设计变量,D为其可行域,En为设计空间。本文目的在于求解满足约束条件的质量最优方案,故将质量函数f(X)作为本文的目标函数。
ESO法全称为渐进结构优化法,是连续体拓扑优化设计方法的一种,其认为在优化区域内,结构上低应变能密度或低应力的材料是低效的,可将其删除[5,6],通过将此类单元在多次迭代中不停舍弃,剩下的单元将趋于最优,从而实现整体结构轻量化的目的。其具体步骤如下:
(1)给定外部载荷以及边界条件,明确初始优化区域,并将该区域网格化。
(2)静力学分析。
(3)明确强度理论。本文采用von Mises应力准则,利用有限元理论将网格化后的模型进行求解,求出每个单元的应力值及单元的von Mises应力和最大的单元应力,如果满足:

则认为该单元可以删除(单元处于低应力状态,即无效状态)。其中,RRi为删除率。
(4)迭代以上计算步骤,直至计算溢出,无法满足式(2)条件,即已达到对应于RRi的稳定状态。此时引进参数进化率ER,以便迭代继续,从而下一稳定状态删除率修改为

(5)将以上步骤迭代,直至结构重量、最大应力或刚度达到预期值。
ESO法虽广泛应用于拓扑优化研究中[7],在解决实际问题时也有许多成功算例,但其本身也存在缺陷,即存在数值不稳定的现象。
2 基于单元生死功能的拓扑优化方法
本文所述的拓扑优化方法是基于渐进结构优化法ESO的基本指导思想的改良,通过配合周界约束法以减少ESO法的数值不稳定现象。
单元生死功能的实现并不是软件将“杀死”的单元从模型中删除,而是将其刚度、强度或其他分析特性矩阵乘以一个很小的因子,导致其最终效果的传递能力为0,例如载荷等,从而实现其质量、阻尼、比热和其他项值为0。死单元的质量将不包括在模型求解结果中。本文利用单元生死功能,通过划定优化区域,设定应力阈值,在不停迭代过程中将低效单元“杀死”,最终获得最大承力结构[8]。最后利用ANSYS的优化模块对最大承力结构进行尺寸优化,从而获得最优腕臂截面。
3 拓扑优化计算模型
接触网腕臂结构系统的主要受力大部分由平腕臂、斜腕臂结构承担。腕臂结构的SolidWorks模型如图1所示。

图1 腕臂结构实体模型
图中受力模型可简化为梁杆结构,平斜腕臂为梁单元,支撑为杆单元,整体结构受力较为简单。考虑到制造工艺等实际因素限制,本文仅考虑等截面优化。由于拓扑优化迭代次数较多,进一步对模型进行优化。考虑到平斜腕臂均受到垂直于轴线的拉压力、弯矩,外部条件基本相同,故选取一段空心圆柱体用于模拟分析平斜腕臂受力情况[9]。
外部边界条件为将一面固定,在另一面施加垂直向下的压力以模拟杆件受力情况。网格划分后模型[10]如图2所示。

图2 等径圆柱体结构模型
4 拓扑优化及受力分析
首先对等径圆柱体进行静力学分析计算,找出其受力差距较大的单元。图3所示为模型结构应力仿真结果。
由图3(a)可知,结构上下部承力点较多,大部分承力点分布在圆截面上下部位置,最大应力209.79 MPa,最大位移36.107 mm。
图3(b)为将结构应力图切片显示,可以看出,结构受力最大区域集中在圆截面上下部,而圆心中轴线上的部位受力较小,符合力学结构逻辑。
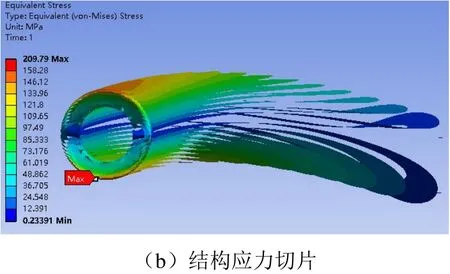
图3 模型结构应力

由此初步判断,拓扑优化可将两边结构减薄,增加垂直中轴线方向的单元。重新建立有限元模型,采用实体圆柱体进行分析计算。
边界条件中,将刚度、固有频率作为约束条件,整体质量作为目标函数,同时加入风载荷、其他结构件造成的扭矩等外部因素影响,对结构进行拓扑优化。结构变化及优化结果如图4、图5所示。

图4 不同迭代次数下结构变化

图5 最终优化结果
由图5可知,等径圆柱结构优化后为由细到粗的圆锥形结构,最末端为椭圆形。考虑到拓扑优化为空间结构优化,本文仅针对横截面进行探讨。杆件典型弯矩曲线如图6所示。

图6 杆件典型弯矩曲线
由计算结果可知,横截面最优形式应为椭圆形结构。根据计算结果修改外形尺寸,剔除无用单元,重新建立三维模型,并对其进行静力学分析,结果如图7所示。

图7 优化结构应力
椭圆形断面结构最大应力出现在上下部位置,为220.4 MPa,最大位移为36.649 mm。
圆形截面与椭圆形截面结构计算结果汇总如表1所示。
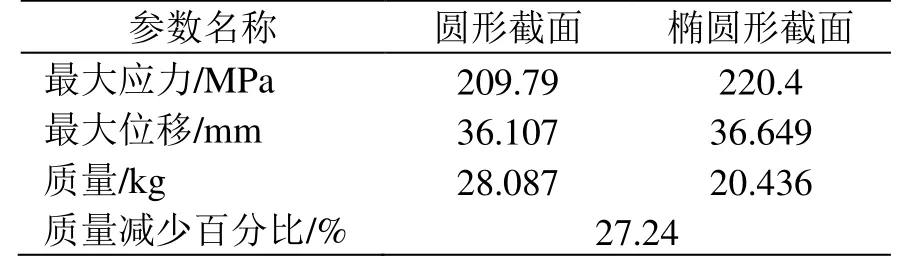
表1 不同截面形式计算结果
刚度为限制接触网腕臂结构的最重要因素,以往计算中,在强度有很大裕量的前提下均会出现刚度首先不满足规范要求的情况。本文中圆形和椭圆形截面结构两者刚度差距不大(最大位移均约为36 mm),但其本身质量则相差27.24%。故在不改变其他外形尺寸、材料以及外部条件的前提下,腕臂整体结构可以减重27.24%,优化量相当可观。通过对优化后结构进行的静力学分析也可知,新截面在结构受力能力上并无衰减。
5 结论
本文利用拓扑优化理论对接触网腕臂结构进行了分析研究,首次将拓扑优化理论与腕臂横截面优化相结合,并对优化前后的模型进行了力学计算。
由计算可得,在相同外部条件要求的前提下,接触网腕臂系统最优截面形式为椭圆形。与传统圆截面相比,在刚度性能保持一致的前提下,椭圆形整体结构可减重约27%。计算结果符合经典力学逻辑,与实际情况相符。椭圆形截面在起重机行业应用已较为广泛,尤其是重型、超重型起重机,也进一步证实椭圆形截面结构的合理性。
接触网腕臂系统由于在电气化铁路中应用广泛,腕臂系统的优化设计对降低项目建设、后期运营维护成本均起到极大的作用,同时也为我国自主研制具有中国特色的接触网腕臂系统装备提供了数据支持和新的设计思路。

