液态水含量对寒区海上风力机叶片霜冰结冰的影响
曹慧清 白旭 尹群
(江苏科技大学,船舶与海洋工程学院,江苏 镇江 212003)
0 引言
近年,风力发电行业发展迅猛,陆上风力发电已趋近饱和,许多企业纷纷把目光转向海上风力机的建设。而处于寒冷地区的海上风力机在冬季运行时将存在结冰的风险,风力机结冰(如图1)影响其气动性能和运行安全,给风力机带来了极大危害。例如,风力机表面结冰会降低风能利用系数,减小出力;影响风力机的结构强度与疲劳寿命,产生安全隐患。因此,研究海上风力机结冰预报与防除冰技术至关重要。

图1 风力机叶片结冰Fig.1.Wind turbine blade icing
为了精确地对寒区海上风力机的结冰进行预报,首先需要研究影响风力机结冰的因素,包括环境温度、液态水含量(Liquid Water Content,LWC)、平均水滴直径(Medium Volume Droplet Diameter,MVD)、风速等。其中液态水含量(单位体积的空气中所有液态水的质量)是影响结冰形状的重要参数,结冰形状改变将影响叶片的气动性能,最终影响风能的转化效率。空气中液态水含量首先取决于地域特性,潮湿气候条件下,液态水含量较高;其次取决于环境温度,温度低于–10℃,空气中过冷水滴凝结为冰晶并降落到地面,使得空气中液态水含量降低[1]。同时,已有研究表明,空气中的气态水含量几乎不会对叶片结冰造成影响[2]。因此,本文以空气中液态水含量为主要研究对象。
目前,已有国内外学者对风力机叶片结冰进行了相关试验研究。孙策[3]研究了霜冰结冰条件下,结冰对风力机叶片的影响,初步提出了一套适用于小尺度、小缩比和霜冰条件下的叶片结冰形状相似准则,利用自行搭建的结冰风洞试验系统完成了对该准则的验证性试验。Shin 和Bond[4]研究了不同的液态水含量、风速等参数对NACA0012 翼型结冰的影响,并做了大量结冰试验。Bose[5]对直径为1.05 m 的水平轴风力机做了降水结冰的试验,得到了叶片不同位置处明冰结冰的形状,发现大多数的明冰都发生在叶片前缘和翼尖处。Hu 等[6]研究了叶片受不同参数影响的结冰分布。结果表明,冰的质量和厚度从叶根到叶尖呈线性增长。较高的风速、较小的攻角、较高的液态水含量和较低的温度均对叶片结冰有较大影响。
相比于风力机风洞试验研究,数值模拟研究更加广泛。Homola 等[7]研究了NREL 5 MW 风力机模型因结冰造成的性能损失,并在霜冰条件下对沿叶片的五个截面结冰进行了模拟,并用计算流体力学(Computational Fluid Dynamics,CFD)方法模拟分析了洁净和结冰翼型截面的气动特性。顾声龙等[8]利用Fluent UDF(User Defined Function)对水平轴风力机叶片翼型的明冰结冰进行了数值研究,得出了明冰对翼型气动性能的影响。邓晓湖等[9]通过CFD 方法对水平轴风力机叶片翼型的霜冰结冰进行了数值模拟,结果表明,结冰后翼型提前进入失速区是造成叶片气动性能恶化的主要原因。结冰模型用于模拟在结冰条件下某结冰对象在流体与结构之间的相互作用关系。目前存在2 种常用冰积模型:一种是结冰经验模型,最常见的是Makkonen 模型[10],该模型是基于准三维、较灵活的框架模型,是其他大多数结冰经验模型的基础;另一种是结冰理论模型,分为二维和三维叶片结冰模型,著名的结冰仿真商业软件LEWICE、FENSAP-ICE 和TURBICE 都是此类模型,其中TURBICE 和LEWICE 为二维叶片模型,FENSAP-ICE 为三维叶片模型。现阶段,二维模型求解空气流场使用的是面元法,主要用于求解势流模型;而三维模型求解空气流场使用的是空间网格法,用于求解N-S 方程或欧拉方程。
海上风力机有着区别于陆上的独特气象条件,陆上的结冰预报方法是否适用仍需验证。由于叶片是风力机接受风能最重要的部件,本文针对寒区海上风力机叶片,采用Fluent 和FENSAP-ICE相结合的方法,选取液态水含量作为敏感参数,分析液态水含量的变化对结冰厚度、结冰量和结冰外形的影响。
1 结冰气象条件与结冰理论
1.1 结冰气象条件
空气中的水滴只会在低于–40℃时自发结冰[11],而温度在0~–40℃之间时,水滴处在亚稳定状态即过冷状态,经过很长一段时间后产生结晶核才会结冰。但是,若水滴与叶片发生碰撞,叶片便会开始结冰。
风力机叶片结冰按其结冰性质可分为霜冰、明冰、湿雪和混合冰。图2 为霜冰、明冰与风速和温度的关系。本文海上风力机的气象条件以Drage 和Hauge[12]的研究为参考,他们通过实验确定了挪威西海岸Brosviksåta 山大气结冰的气象条件范围(见表1)。结合表1 和图2 可知,本文研究的结冰类型为霜冰。同时,世界气象组织指出,海平面以上16 m 是海洋飞沫的上限[13],本文研究的海上风机叶片叶尖离海平面最近处约30 m,所以本文暂不考虑海洋飞沫对叶片结冰的影响。

图2 冰型与气温和风速的关系[14]Fig.2.Relationship between ice type and temperature and wind speed[14]

表1 气象条件Table 1.Meteorological condition
1.2 结冰机理及模拟
1.2.1 结冰机理
结冰是一种常见的自然现象,从热力学角度来看,水的温度降到0℃以下成为过冷水,过冷水并不稳定,而是处于亚稳态,该状态的解除需要大于临界尺寸的冰核的形成。当过冷水中出现尺寸大于临界尺寸的冰核时,结冰过程开始,冰核在过冷水中长大,最终成为宏观意义上的冰[15]。风力机在运行过程中,当叶片表面周围温度低于0℃并与过冷水滴发生碰撞时,便会出现结冰现象。在结冰过程中,伴随复杂的传热、传质现象,撞击到叶片表面的过冷水滴与空气会产生对流换热、自身伴随蒸发和升华等,同时释放潜热,根据外界条件差异决定是否产生结冰表面的液态水回流等现象[16]。
霜冰主要出现在环境温度较低、液态水含量较低和液滴大小较小情况下,这些条件下过冷水滴撞击到叶片表面立即冻结。结冰过程中释放的热量不足以使叶片表面温度上升到冰点以上,因此冰没有发生融化,也无向后的溢流。所以,结冰发生在叶片前缘狭窄区域,外形较规则且不透明。
1.2.2 结冰数值模拟
采用数值模拟方法进行结冰计算,主要包括3 个步骤:叶片流场计算、水滴轨迹计算和冰层生长计算。
(1)叶片流场计算。计算叶片周围的流场分布,以得到叶片周围空气流速等参数。
控制方程为低速黏流N-S 方程,通用形式为:

其连续方程为:
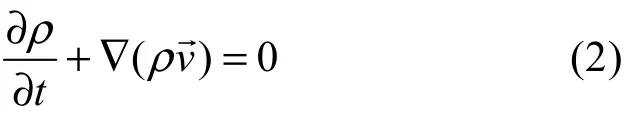
式中,ρ为空气密度,t为时间,φ为运输变量,∇为空气速度,φΓ 为扩散系数,qφ为源项。
风力机工作时叶片处于旋转状态,此时空气处于复杂绕流运动状态,因此本文使用叶素动量(Blade Element Momentum,BEM)理论来解决叶片旋转和多叶片对空气流场的影响[17]。
BEM 理论是分析风力机叶片气动性能主要方法。空气绕流叶片的运动是具有涡旋的复杂流动,BEM 理论是将风轮叶片沿展向分成多个微段,这些微段为叶素,通过引入轴向、切向诱导因子反映气流沿轴向、切向速度的变化,使基于动量守恒原理和气动理论的分析方法成为可能。
数值模拟包括两个主要参数,相对风速(Vrel)和迎角(α0)。这些参数取决于来流风速(V∞)、轴向和切向诱导因子(a和γ)、截面半径(r)、局部速比(λr)和该截面处的叶片扭转角(ϕ)。每个截面的相对风速和迎角通过下式计算:

其中:
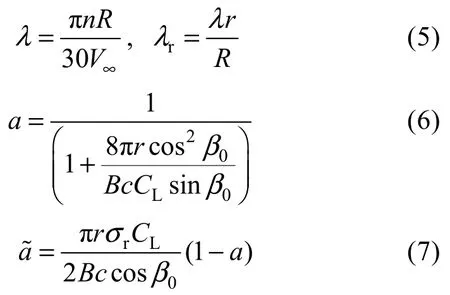
其中,R是风轮半径,CL为升力系数,B为叶片个数,c为叶片翼型弦长,λ为叶尖速比,λr为局部速比,β0是流动角,β0=90−α0−φ。
(2)水滴轨迹计算。水滴轨迹的计算使用的是FENSAP-ICE 软件中DROP3D 模块,在叶片流场计算结果的基础上,求解过冷水滴的运动方程,对每个水滴进行跟踪,以确定水滴是否与叶片发生碰撞。用欧拉法建立气-液两相控制方程,然后用有限体积法求解控制方程,从而得到水滴运动轨迹和叶片表面的撞击特性。
水滴轨迹运动方程如下:
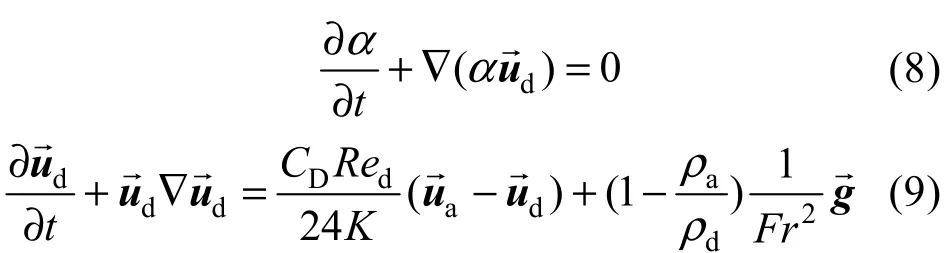

式中,ρa和ρd分别为气流密度和水滴密度,Vrel为相对风速,和分别为气流速度和水滴速度,d为水滴直径,aμ为运动黏度,L∞为特征长度,g∞为来流重力加速度,→为重力加速度。
(3)冰层生长计算。冰层生长计算运用FENSAP-ICE 软件中ICE3D 模块,此模块使用的是Bourgault 结冰模型,利用质量和能量守恒方程求解叶片表面的结冰热力学模型,得到叶片的表面温度和结冰量的分布。
质量守恒方程:

能量守恒方程:

式中,f表示水膜,为瞬时蒸发质量,为瞬时结冰质量,fρ、fc、sc、ε、σ、Levap和Lfusion分别代表流体的物理性能,Qanti-icing为防冰热通量,为表面法线向量,LWC为局部液态水含量,β局部水滴收集系数。各项的具体表达式和方程的详细求解方法参见文献[18]。
当结冰类型为霜冰时,液滴撞击叶片表面会直接结冰,则不需考虑传热及相变,只需考虑质量守恒。其质量守恒方程可以写为:
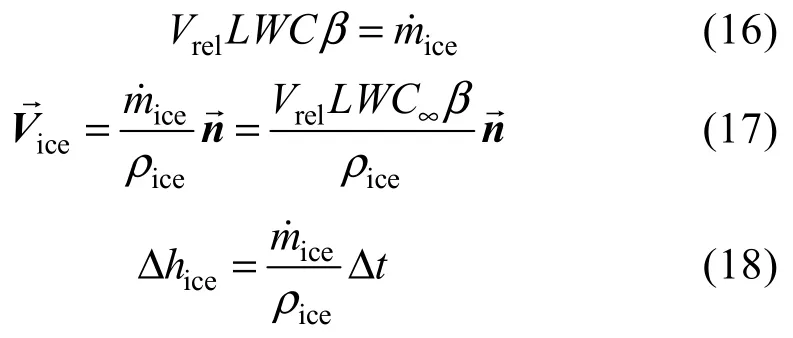
式中,ρice为冰的密度,tΔ 为时间步长,为结冰增长速度,Δhice结冰表面位移,LWC∞为来流液态水含量。
结合公式(16)~(18)可以看出,在其他参数条件给定时,LWC的改变会直接影响到叶片的结冰质量和结冰生长速度。
2 数值预报方法及验证
2.1 计算外形及网格
本文计算外形选用某5 MW 级海上风力机[19],其单叶片长63 m。风力机叶片(见图3)上距离翼根85%~100%之间的区域对于风力发电而言最重要,本文采用位于风力机叶片上距离翼根90%的位置的翼型作为研究对象[20]。此处的翼型为NACA64-A17,翼型弦长为2.086 m,厚度为0.05 m。
光滑翼型与带冰翼型均采用ICEM 划分的C型结构化网格(见图4),翼型固壁面采用无滑移和绝热条件。

图4 计算域网格划分及局部放大图。a) 洁净翼型计算域网格划分情况;b) 洁净翼型局部网格划分情况;c) 结冰翼型局部网格划分情况Fig.4.Grids in computational zone and part grid of the airfoil.a) grids in computational zone of the clean airfoil;b) partial grid of a clean airfoil;c) partial grid of an iced airfoil
2.2 计算流程
本文结合Fluent 和FENSAP-ICE 软件进行风力机叶片的结冰数值模拟研究。利用ICEM 软件划分洁净翼型截面网格;将划分好的网格导入Fluent 软件中分析叶片周围流场;将流场分析结果导入FENSAP-ICE 中,在FENSAP-ICE 软件中DROP3D模块计算水滴轨迹,ICE3D 模块计算结冰生长并导出结冰后翼型;由于霜冰主要发生在翼型的前缘,翼型前缘需加密处理,重新在ICEM 中划分结冰后的翼型截面网格并导入Fluent,重复上述过程直到给定的截止时间。图5 为本文的计算流程图。
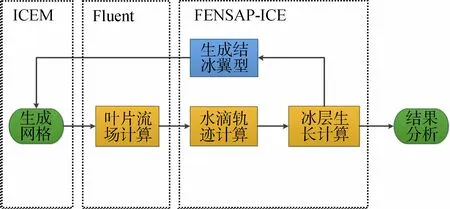
图5 计算流程Fig.5.Calculation process
2.3 数值验证
为了验证本文数值模拟结果的准确性,本文将数值模拟结果与试验结果进行对比。其中,NACA0012 翼型结冰的数值模拟是最经典的算例,有着丰富的冰风洞试验数据。Shin 和Bond[21]在美国国家航空咨询委员会(NACA)的Lewis 研究中心对NACA0012 翼型结冰进行了多次冰风洞试验,积累了大量的试验数据,本文选取其中一组试验结果进行对比。
文献中的计算条件为:翼型弦长c=0.5334 m,攻角AOA=4°,环境温度T=–28.3℃,来流速度U∞=67.05 m·s–1,平均水滴直径MVD=20 μm,液态水含量LWC=1 g·m–3,结冰时间t=360 s。
由图6 可知,本文预测冰形与试验结果吻合较好,结冰外形为霜冰,霜冰主要集中在翼型前缘,结冰极限与结冰厚度基本一致,结冰冰形大部分重合,由此验证了本文计算方法的正确性。

图6 本文计算结果与试验结果对比Fig.6.Comparison of the ice shape between this paper and the experiment
3 液态水含量对叶片结冰的影响
3.1 计算条件
本文采用了如表2 所示的环境条件和气象条件,以此来计算翼型表面的结冰量和结冰外形,并分析不同液态水含量和在1 h、3 h 和10 h 三种不同结冰时间条件下对叶片结冰的影响。
3.2 时间步长选择
在结冰数值模拟的计算中,时间步长的选择会对数值模拟的计算结果造成干扰。随着翼型结冰后表面局部收集系数β的改变,结冰数值模拟的计算结果也受到影响。对于CFD 分析软件来说,时间步长选取的越小,计算结果越精确,但对计算机的性能要求越高,计算时间也随之增加,因此有必要选取合适的时间步长。
本文选取表2 中一组结冰条件进行研究,其中液态水含量为0.15 g·m–3,结冰时间为3 h,其他结冰条件不变。时间步长分别选取5 min、15 min和30 min,表3 为三种不同时间步长时的数值计算结果。从表3 中可知,相较于时间步长为5 min 时的结冰量,15 min 和30 min 时间步长下结冰量的变化幅值百分比分别为 1.30%和4.84%。三种时间步长模拟结果相近,但在计算中发现,随着结冰时间的增加,15 min 和30 min相较于5 min 时间步长下结冰量的变化增幅呈不断增大的趋势。因此,考虑到三种时间步长下的计算效率和计算精度,本文选取15 min 作为时间步长。

表2 不同液态水含量对结冰影响的计算参数Table 2.Calculation parameters of influence of different liquid water content on icing

表3 三种时间步长数值计算结果Table 3.Three time-step numerical calculation results
3.3 不同液态水含量下的计算结果分析
图7 至图9 分别为液态水含量为0.05 g·m–3、0.10 g·m–3、0.15 g·m–3、0.20 g·m–3和0.25 g·m–3时,在1 h、3 h 和10 h 三种不同结冰时间条件下,叶片所取截面的结冰量、结冰最大厚度和结冰形状图。

图7 不同液态水含量下叶片表面的结冰量Fig.7.Amount of icing on blade surface under different liquid water content
从图7 和图8 可以看出,在相同的结冰条件下,随着空气中液态水含量的增加,翼型表面的结冰量和结冰厚度也逐渐增加。这是由于液态水含量代表单位体积空气中所含有的液态水的质量,在其他条件相同的情况下,随着液态水含量的增加,单位体积空气中存在着更多的水滴,将有更多的水滴撞击到叶片表面,从而使叶片表面微元中收集到的液态水更多,并在之后的传质和传热过程中冻结,形成更多的冰。同时,从图中可以看出,随着结冰时长的增加,不同浓度液态水含量下结冰量的增幅呈不断变大的趋势。这是由于随着结冰时间的增加,不同浓度液态水含量下结冰外形差异更加明显,结冰表面的局部收集系数β也随之变化,因此结冰量不再随液态水含量变化呈线性增加。

图8 不同液态水含量下叶片表面的结冰最大厚度Fig.8.Maximum thickness of icing on blade surface under different liquid water content
从图9 中可以看出,不同浓度液态水含量下生成的冰形均为霜冰,未发现明显溢流现象。液态水含量的改变并没有改变叶片表面的结冰类型,也未影响结冰的生长趋势。不同浓度液态水含量下,冰与叶片的吸附面没有产生明显变化,这是因为尽管空气中液态水含量增加了,但风速、平均水滴直径等参数并未发生改变,水滴的运动轨迹也没有改变。
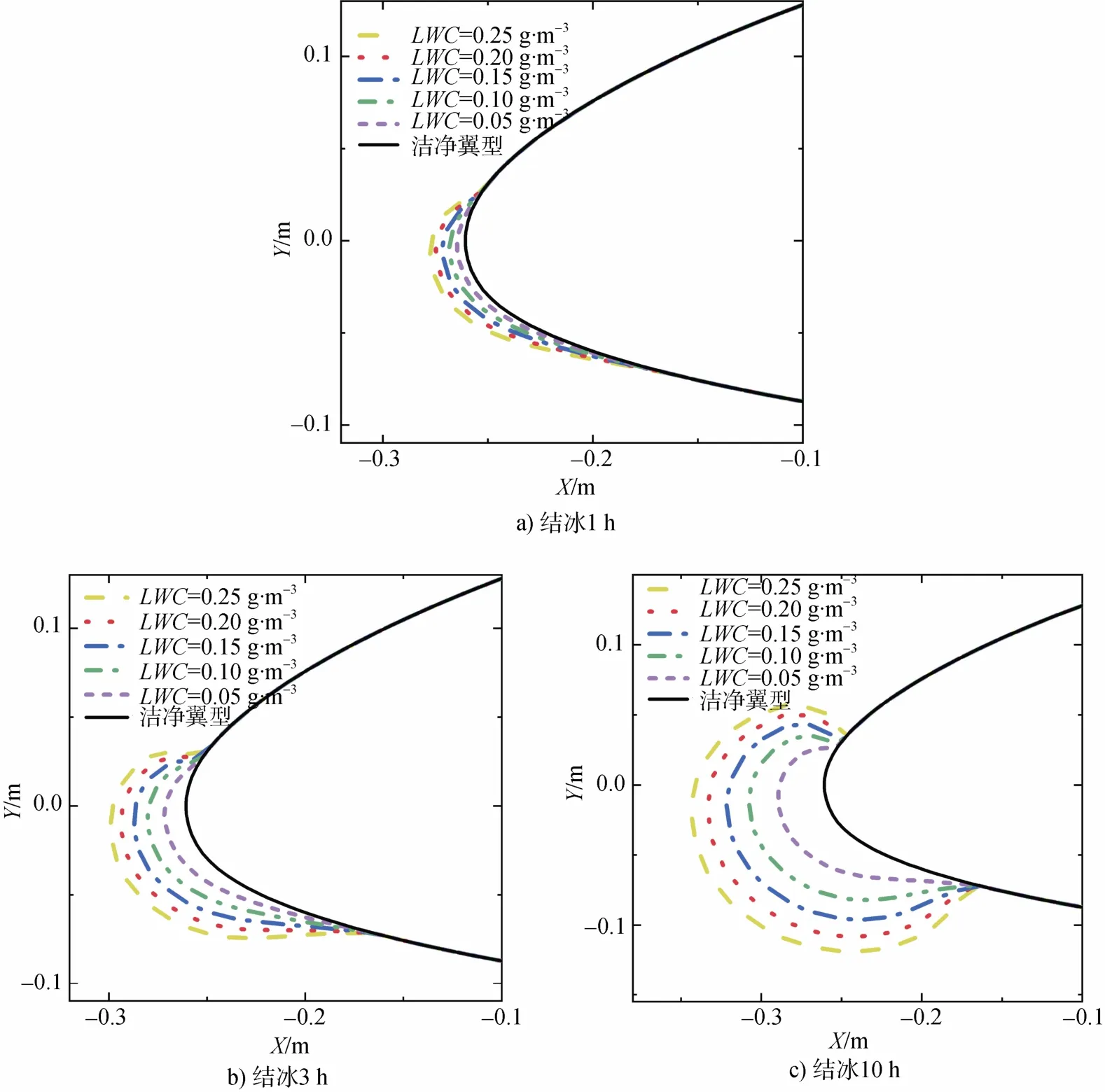
图9 不同液态水含量下叶片表面的结冰外形。a) 结冰1 h;b) 结冰3 h;c) 结冰10 hFig.9.Shapes of icing on blade surface under different liquid water content.a) 1 h-icing;b) 3 h-icing;c) 10 h-icing
4 结论
本文以寒区海上风力机叶片结冰为背景,采用Fluent 和FENSAP-ICE 相结合的方法对叶片结冰开展数值模拟,选取液态水含量作为敏感参数,分析了液态水含量的变化对叶片结冰厚度、结冰量和结冰外形的影响,得出如下结论。
(1)液态水含量在0.05~0.25 g·m–3范围内,随着液态水含量的增加,叶片表面的结冰量和结冰厚度随之增加。
(2)液态水含量在0.05~0.25 g·m–3范围内,液态水含量并不影响叶片表面的结冰类型和结冰生长趋势,同时冰与叶片的吸附面也不随液态水含量变化而改变。
(3)采用不同的液态水含量对叶片结冰进行模拟,虽然模拟出了寒区海上液态水含量的变化范围,但是液态水含量会随海拔高度变化而变化,本文研究的海上风力机塔架高达90 m,叶尖高度可达海平面以上153 m,叶片旋转时,短时间内会掠过不同液态水含量的空气,对液态水含量时刻变化的空气的模拟还有待改进。
(4)针对不同结冰时长、不同液态水含量的结冰进行了分析。若风速、平均水滴直径等参数发生改变,对不同液态水含量下的结冰进行对比分析,是否能得到类似的结论还有待研究。

