基于DP-SQP方法的列车动态编组优化控制

李建雄,王海峰,2,3,张启鹤,柴 铭,2,3

(1.北京交通大学电子信息工程学院,北京 100044； 2.北京交通大学轨道交通运行控制系统国家工程研究中心,北京 100044； 3.北京交通大学城市轨道交通北京实验室,北京 100044)

引言

列车运行控制系统是保障运行安全和提升行车效率的关键技术装备。行车间隔控制是列车运行控制系统的基本功能之一[1]，在保证运行安全的前提下，缩短行车间隔是提升运输能力的有效方法[2-3]。为此，国内许多地铁线路完成了由固定闭塞到移动闭塞的改造，干线高速铁路也选择使用准移动闭塞行车方式代替固定闭塞。随着列车运行速度的提高，在现有的行车闭塞方式下，必须加大行车间隔以保证列车运行安全。为打破现有闭塞方法的束缚，进一步缩短行车间隔，动态编组逐渐成为研究热点之一[4-5]。

2000年左右，欧洲学者提出使用无线通信代替机械连接，将多列车组成编组车队，可极大地减小行车间隔[6]。这种运行方式可有效提高铁路运输能力[7-9]，欧洲铁路倡议的“Shift2Rail”计划也将其纳入未来轨道交通研究方向。为实现前后列车由绝对制动距离行车状态过渡到车-车通信连接的编组状态，后行列车需在运行过程中动态地加入编组车队[10-11]，这个过程称之为动态编组[12]。实现动态编组的关键是对行车间隔的合理控制。FELEZ等[13]提出了一种基于模型预测思想的列车低间隔追踪控制方法，在保证安全的同时大大降低了行车间距；ZHU等[14]将自适应控制方法作为一种误差修正方案来削弱外部扰动对行车间隔控制的影响。以上对于行车间隔控制的研究是以解决单个问题为目标，但动态编组控制的理想目标是在保证编组精确性的前提下，降低列车牵引能耗，并且可以有效应对外界因素的干扰，故动态编组是一个多目标控制过程。

列车速度曲线优化是一种实现列车多目标控制的有效方法[15]。褚心童等[16]使用蚁群算法实现了快速收敛的ATO曲线优化，该方法计算效率高，但对运行速度和列车工况做了离散化处理，对列车运行模型建立得不够精确，很难达到最优的优化效果；王攀琦等[17-19]将二次规划算法和模型预测控制方法相结合，实现了铁路列车和公路汽车运行曲线的在线优化，该方法对列车运行模型描述精确、计算效率较高，但由于模型预测方法的预测时域范围有限，不能对动态编组全局过程实现优化控制；MIYATAKE等[20]比较了几种全局优化控制方法的优劣，其中，动态规划方法优化效果较好，但计算效率过低，只适合于离线优化；二次规划方法在计算效率和模型建立的复杂度之间取得了较好的平衡。综上所述，精确建立列车运行模型和提高计算效率是列车曲线优化的关键，并且模型建立的精确性将会影响控制效果。

动态编组是对控制效果和计算效率都有较高要求的控制过程。对于一般优化方法，模型建立过于细节化将会降低求解时的计算效率，从而不能实现在线控制[21]。为此，以离线速度曲线计算和在线最优控制相结合为基础，提出一种基于动态规划-序列二次规划的列车动态编组优化控制方法。

1 动态编组过程

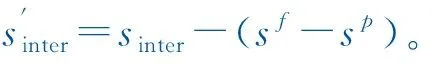
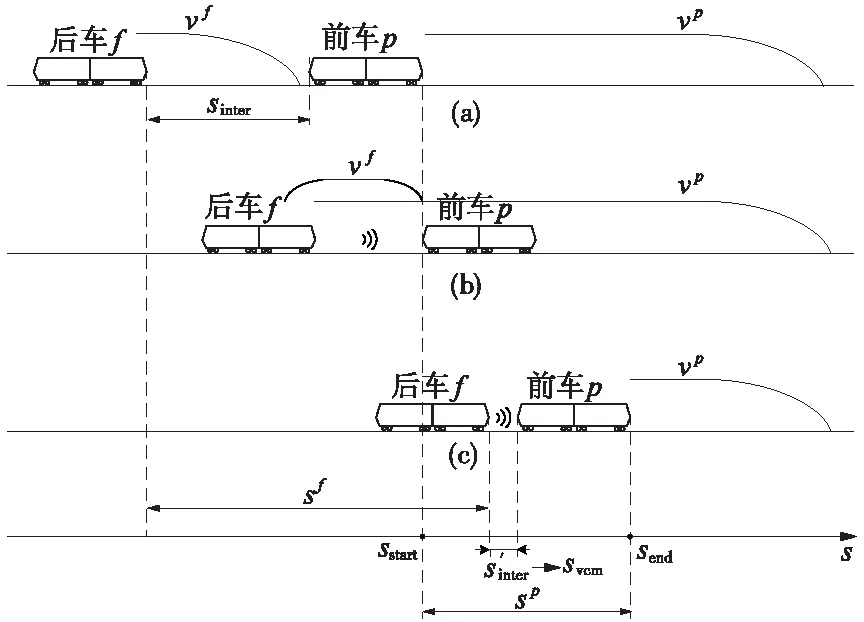
图1 动态编组场景

完成动态编组后，两车保持低间隔的编组运行状态。前后列车通过车-车通信交换各自的位置、速度和加速度等运动参数，前车根据地面发送的行车许可运行，后车跟随前车的状态行车，与前车采用同步的速度、加速度，来维持两车间隔在一定范围内。

2 动态编组数学模型

动态编组数学模型的建立是使用优化方法实现编组控制的前提。首先，建立列车动力学方程，描述列车的运动状态；然后，对列车牵引能耗和精确编组建立方程，以便优化方法目标函数的建立。

2.1 动力学方程

采用基于纵向的列车动力学方程对动态编组列车的运动状态进行描述。将列车看作一个具有驱动/制动系统且受到空气阻力、坡道阻力、曲线阻力的单质点[22]。列车所受合力表示为

F(u，v)=u-Fb(v)-Fα-FR

(1)

其中，Fb(v)=C0+C1v+C2v2；Fα=Mgα；FR=ηM/R。

式中，F(u，v)为列车所受合力；v为列车速度；u为列车控制驱动力/制动力，是与列车运行方向相同/相反的控制力；Fb为空气阻力；Fα为坡道阻力；FR为列车曲线阻力；C0、C1、C2分别为列车的空气阻力相关系数，是依赖于列车特性的参数；M为列车质量；α为轨道坡度；η为曲线阻力相关系数；R为线路半径。

由于受列车输出功率和加速度的限制，驱动/制动力uk受以下约束

-Mab≤F(u，v)≤Mad

(2)

-Pb≤uv≤Pd

(3)

式中，ad为最大输出驱动加速度；ab为最大输出制动加速度；Pd为最大驱动功率；Pb为最大制动功率，在该模型中ad、ab、Pd、Pb恒定。定义上述约束为u∈U。

2.2 能量消耗方程

在动态编组时列车克服阻力和提升速度所消耗的能量为列车牵引能耗，能耗方程的建立是实现低能量消耗目标的基础。根据能量守恒定理建立能耗方程，即

(4)

P(t)=F(t)v(t)

(5)

式中，e为列车总牵引能耗，表示为功率对时间的积分；T为总编组时间；P为列车的瞬时输出功率；u为列车的牵引力。文中忽略了能量在列车传动系统中的损失，并且假设列车不能回收制动能量，所以当列车主动制动时牵引能量消耗为零。

2.3 精确编组方程

在动态编组结束时刻，前后列车需达到理想的编组间隔，以实现精确编组的目标。精确编组方程的建立可以帮助判断列车是否达到精确编组状态。建立方程如下

serror=sf-sdes

(6)

sdes=sp+sinter-svcm

(7)

式中，serror为编组误差，是编组过程后车实际运行距离sf和目标运行距离sdes之间的差值， 在动态编组结束时刻中，编组误差越小，表示后车的行车距离越接近目标距离，越能达到精确编组目标。目标运行距离是列车在编组过程中理想的运行距离，计算如式(7)所示，sp为编组过程前车的总运行距离；sinter为编组开始时刻两车间距；svcm为理想的编组间隔。

3 动态规划-序列二次规划控制方法

动态规划算法具有模型描述精确、优化结果质量高的优点，但由于计算效率较低，只能用于离线计算。序列二次规划算法计算时间短，但对于初始解异常敏感，在无法获得良好初始解的情况下，该方法的优化控制效果较差。将两种算法结合，离线状态下使用动态规划算法获得最优速度曲线，将离线结果作为初始解，使用序列二次规划在线求解最优控制策略。

3.1 离线动态规划编组曲线计算

首先，对编组时间进行阶段划分，将列车动态编组控制问题转化为多阶段最优化决策问题；然后，将子区间速度作离散化处理，结合动力学模型获得用于连接各子区间离散速度值的状态转移方程；最后，建立目标函数和约束条件，利用动态规划的无后效性原理进行求解，获得最优速度曲线。

(1)编组时间阶段划分：在时间维度下，可以监督前后列车在同一时刻下的位置关系，保障运行安全，因此，本文选择时间划分方法。编组过程总用时为编组时间，根据前车在编组区间的速度曲线获取编组时间。假设前车速度距离曲线已知，且前车可以按照该曲线行车。将编组区间等距离划分成n段，获取在每段开始和结束时的前车速度，通过速度时间积分关系，结合历史运行数据计算前车在各段中的运行时间Δtk(k=1，2，…，n)。按照每个子区间时间长度为Δtk的规则对编组时间进行阶段划分。定义各子区间的开始时刻为驱动力/制动力决策阶段，各决策阶段控制力组成的操作序列即列车动态编组的控制策略。

以时间划分编组过程后，在时间子区间内的列车位置将不能确定，因此，不能确切得知列车所处的线路坡度、曲率半径和限速等线路信息。但鉴于编组过程时间较短，假设整个编组区间的坡度曲率和限速值已知且恒定。

(2)速度离散化：为提高求解效率，降低搜索空间，对各决策阶段的允许速度作离散化处理，如图2所示。其中，最大限制速度是线路限速，最小限制速度为前车速度。将前车速度作为最小速度限制是为保证后车始终快于前车，以实现在编组结束时刻两车间隔达到最小，避免在编组过程中由于两车间隔过小引发追尾事故。

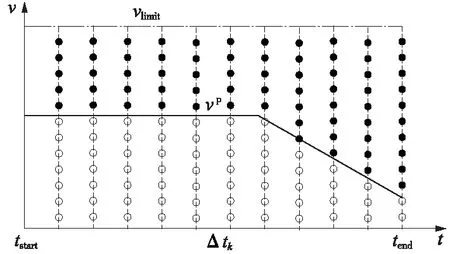
图2 离散允许速度

图2中tstart和tend分别为编组开始时刻和结束时刻，两者之差即编组时间；Δtk为各子区间的时间长度；vlimit为线路限制速度；vp为前车速度。图中圆点表示离散化的速度值，其中，实心圆点表示允许速度值。速度的离散化精度将影响计算复杂度，具体精度选择将在后文介绍。

(3)不同速度下的状态转移：列车状态转移关系表达了单个子区间开始速度、终点速度、驱动力/制动力和运行时间之间的关系。假设在单个子区间内的驱动力/制动力恒定，在列车动力学模型的基础上结合复合梯形公式，得到状态转移满足以下关系

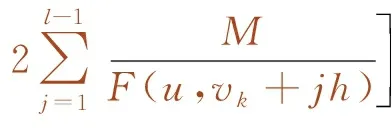
(8)

其中

(9)

式(8)表示在不同驱动力/制动力u下从vk转移到vk+1的时间消耗为Δtk，F为列车所受到的合力，由式(1)计算获得。式(9)表示将单个子区间的速度变化等分成l份，这种方式提高了状态转移描述的精确程度。

子区间的初始速度和终点速度决定了决策阶段应采用的控制力大小和子区间的运行距离。根据式(10)和式(11)获得vk到vk+1状态转移下的控制力uk和运行距离Δsk。

uk(vk，vk+1)=

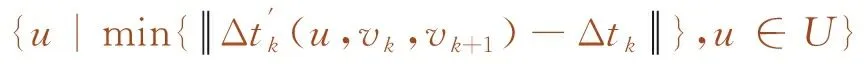
(10)

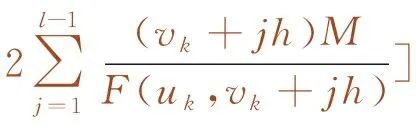
(11)

(4)目标函数约束条件建立：目标函数是衡量控制策略优劣的数量指标。根据动态编组的目标要求建立目标函数如下

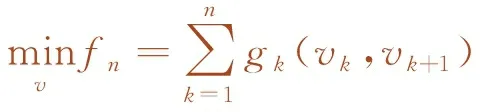
(12)

其中

gk(vk，vk+1)=ek(vk，vk+1)+λΔsk(vk，vk+1)

(13)

ek(vk，vk+1)=

(14)

式(12)表示编组过程能量消耗和运行距离的指标函数，也是动态规划算法求解时的目标函数。gk表示第k个子区间的阶段指标，式(13)中λ为关系系数，用于在迭代计算中调整总能耗和总运行距离的大小关系。ek表示列车在k子区间由vk迁移到vk+1的能量消耗，为获得更加精确的能耗，当速度vk、vk+1不等时，将单个子区间按照速度变化划分，根据能耗模型获得该区间的能耗值。

(15)

式(15)表示运行距离应被约束在目标距离的误差允许范围内，用于验证动态规划计算结果是否满足精确编组目标，其中，svar为允许的编组误差最大值。因为单个区间运行距离的改变将会对整体编组精度产生影响，而动态规划算法的使用前提为无后效性，故将运行距离作为验证目标可以方便问题的求解。在编组结束时刻，若列车状态满足式(15)的约束，则称之为精确编组。

建立约束条件

uk=uk(vk，vk+1)

(16)

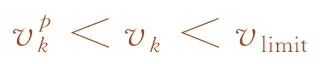
(17)

uk∈U

(18)

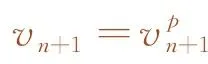
(19)

其中，∀k=1，2，…n，n+1。

式(16)是状态转移约束，表示子区间内不同速度变化与驱动力/制动力的关系；式(17)是速度约束；式(18)是驱动力/制动力约束；式(19)是速度终端约束，表示编组结束时刻前后列车速度应保持相同。

(5)动态规划求解：动态规划的求解方法核心是将原问题转化为一系列单一问题，使用动态规划顺推解法求解，递推方程如下

fk(vk+1)=min{fk-1(vk)+gk(vk，vk+1)}，

vk∈V，f0=0

(20)

其中，fk(vk+1)为第k子区间的终点速度为vk+1时，从编组开始到第k个决策阶段的指标最优总值；V为第k子区间开始速度的可取范围。

列车若按照理想速度控制行车，则可以在规定区间内完成编组任务。但在实际运行过程中，由于存在外界干扰等不确定因素，列车的实际运行曲线可能与理想速度曲线产生偏差，继续按照离线行车策略控制列车将不能完成动态编组，甚至发生追尾的危险，需对编组过程进行在线实时控制来纠正偏差。但动态规划方法对模型建立精确、求解过程迭代次数多，导致计算时间长，因此，使用动态规划方法实现在线实时控制是不可行的。

3.2 序列二次规划在线最优编组控制

序列二次规划(SQP)在线控制方法用于列车处于偏离状态时的动态编组控制。在列车编组过程中，当实际速度与理想速度的偏差超过某临界值时，即为偏离状态。SQP在线控制的实现步骤如下：首先，在监测到偏离状态的时刻，列车计算剩余编组时间，使用与离线动态规划相同的划分规则对剩余编组时间进行阶段划分；然后，通过车-车通信获得前车的位置、速度等数据，计算两车当前位置间隔，并建立动态编组最优化问题；最后，使用SQP算法求解最优控制策略实现在线控制。

在线控制的目标是纠正外界干扰带来的速度偏离，以保证在编组结束时刻列车间距离接近理想间隔，并最小化能量消耗。优化问题描述如下。

目标函数

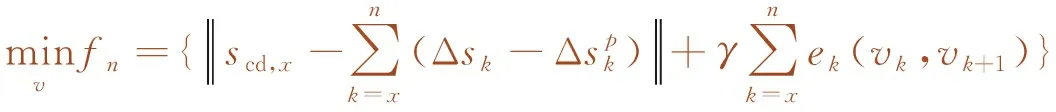
(21)

约束条件

uk=uk(vk，vk+1)

(22)

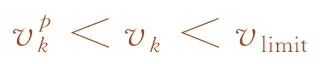
(23)

uk∈U

(24)

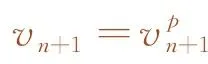
(25)

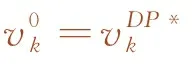
(26)

其中，∀k=x，x+1，…,n，n+1；fn为编组过程的指标函数，由运行距离指标和能耗指标两部分组成；γ为两部分大小关系的系数；x为列车所处的决策阶段。式(21)为目标函数，由两部分组成，第一部分表示前后两车在剩余编组时间的运行距离差与第x决策时刻的协调距离scd，x的差值，在优化算法中通过调整该差值调整后车运行距离，以纠正速度偏差提高抗干扰性能；第二部分表示后车的牵引能耗，其中，ek为单个子区间的能耗值。式(22)是状态转移约束；式(23)为速度约束；式(24)是驱动力/制动力约束；式(25)是速度终端约束；式(26)是初始解约束，以动态规划求解的离线最优解作为优化计算过程的初始解，可提高求解速度。

为进一步缩短最优化问题的求解时间，对状态转移约束和能量消耗计算方法作适当的简化处理：将单个子区间的列车行驶处理成匀变速或匀速运动，状态转移约束式(22)更改为式(27)；采用能量守恒定理计算式(21)中的列车能量消耗ek，如式(28)。

(27)

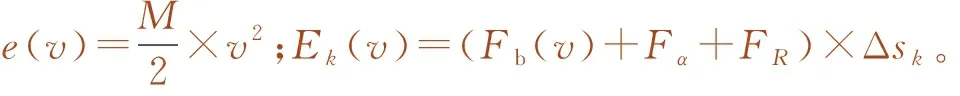
式(28)中，e(vk+1)为子区间结束时刻的列车动能；e(vk)为子区间开始时刻的列车动能；Ek为克服空气阻力和线路阻力的能量。考虑到列车制动时能耗计算结果可能为负数，表示列车回收了制动能量，为与动态规划算法统一，此时的能耗置零。

编组控制问题被转换成非线性最优化问题，使用SQP算法求解获得剩余编组时间内的最优速度曲线和控制策略。在发生偏离后的每个决策阶段使用上述快速SQP算法，则可实现动态编组的在线控制过程。在仿真实验中使用MATLAB中的非线性SQP工具求解该最优化问题。

4 仿真验证

选取实际铁路线路作为动态编组场景，该场景包括待编组的两辆列车，前车按照移动闭塞方式行车，后车使用本文的控制方法执行动态编组。该场景下的环境参数如下：编组区间长2 000 m，限制速度25 m/s，坡度为+1‰，曲线半径1 000 m。仿真实验中设定编组开始时刻两车间距为400 m，理想的编组距离为50 m，在编组区间内，前车速度恒定为20 m/s。

4.1 动态规划方法性能分析

离线动态规划算法的计算复杂度取决于速度离散化精度。离散化精度越高，对列车运行状态的描述越准确，从而获得的控制策略越接近最优结果，但计算复杂度和计算时间也会随之增加。为平衡运算时间和列车状态描述准确性，经过多次不同精度的测试，最终确定选择0.1 m/s作为速度的离散化精度。

编组精确性一般采用编组误差来衡量。编组误差是指理想编组间隔和编组结束时刻实际列车间隔的差值，编组误差越小表示编组精确性越高。该实验下设定允许编组误差最大值为5 m。在离线状态下，使用动态规划方法为后车计算编组曲线，通过二分法寻找最优的关系系数λ及其对应的最优化速度曲线。表1为在迭代过程中不同λ对应的运行距离、编组误差和总运算时间结果，图3为部分迭代过程的后车速度时间曲线。从表1和图3可以得到，经过7次迭代计算，寻找到允许编组误差内的最优结果。在最优速度曲线控制下，后车运行距离为2 353 m，编组误差为3 m，达到了精确编组目的。

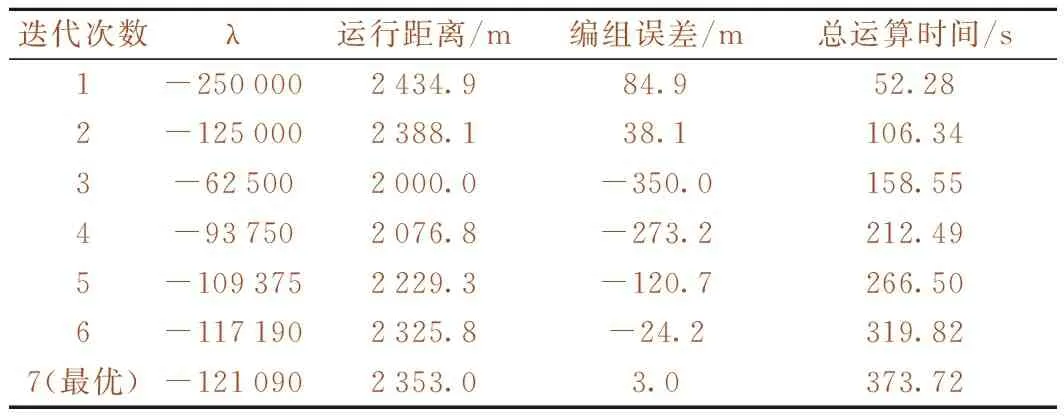
表1 动态编组过程离线动态规划计算结果

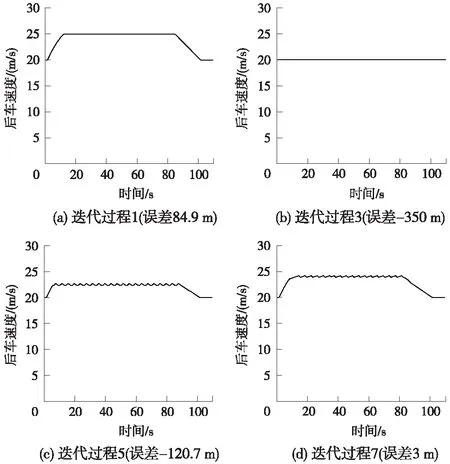
图3 动态规划迭代过程的后车速度曲线

在能耗性能方面，经过多次仿真实验，获得行车距离和最优能耗之间的关系如图4所示。在满足动态编组最优目标的前提下，后车的行车距离和能量消耗呈现正相关关系。在编组误差允许范围内，运行距离越小，能量消耗越低。通过控制式(13)目标函数中的系数λ可以调整运行距离到编组误差允许范围内。

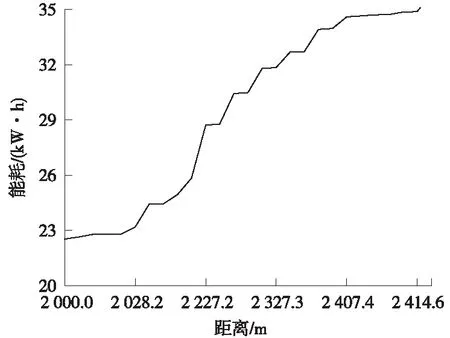
图4 行车距离和最低能耗关系

为进一步证明动态规划方法的有效性，在离线状态下，将其与普通的SQP方法和快速SQP方法作对比。其中，普通SQP优化方法未使用离线速度结果作为初始解，而快速SQP方法使用了动态规划计算的速度值作为初始解。在同样的仿真场景下，列车分别按照3种方法控制列车运行，得到仿真结果如图5和表2所示。

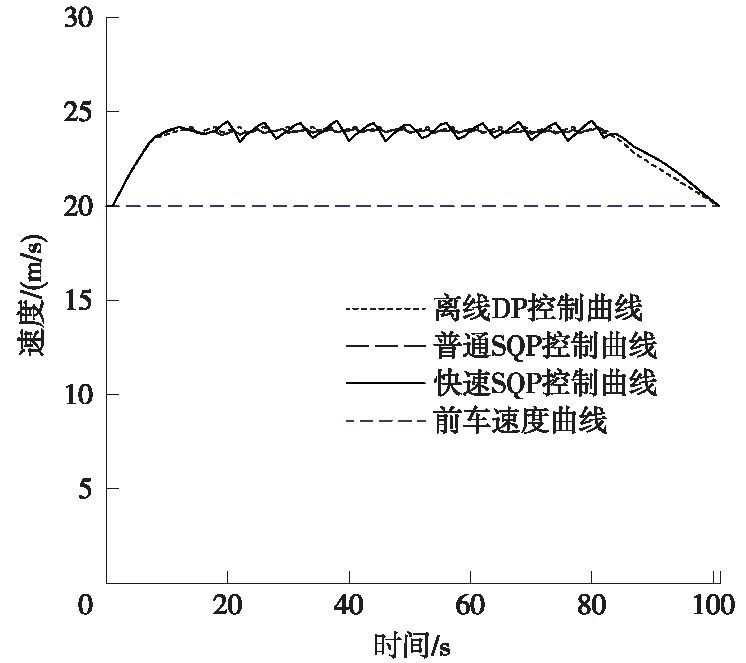
图5 离线状态不同控制方法的列车速度曲线

表2 离线状态下DP、SQP算法性能

图5描绘了离线状态不同控制方法下的后车速度曲线，结果显示3种方法下的列车在编组结束时刻都达到了与前车相同的速度。其中，离线DP和普通SQP曲线基本重叠，且较平滑，而快速SQP方法由于迭代次数少的原因，在20～80s期间曲线有明显的起伏波动。表2比较了不同控制方法下的编组性能和计算时间，其中，普通SQP方法在能耗和编组误差方面与动态规划方法基本相同，但由于没有选择合适的初始解，成功收敛到最优结果的概率只有70%；快速SQP方法下列车能耗达到34.648 3 kW·h，而动态规划方法的列车能耗为32.702 8 kW·h，能耗降低5.6%，节能效果明显；快速SQP方法下的编组误差为25 m，超过允许误差的最大值。快速SQP方法虽然在能耗和编组精确性方面有所欠缺，但平均计算时间保持在1 s之内，计算速度快，并且由于初始解的正确选择保证了成功收敛的概率。

4.2 序列二次规划在线控制方法性能分析

计算效率是实现在线控制的重要指标，本文使用模型的合理简化和将离线结果作为初始解的方法，实现了全局优化问题的快速收敛。图6比较了快速SQP方法和普通SQP算法下的收敛情况。

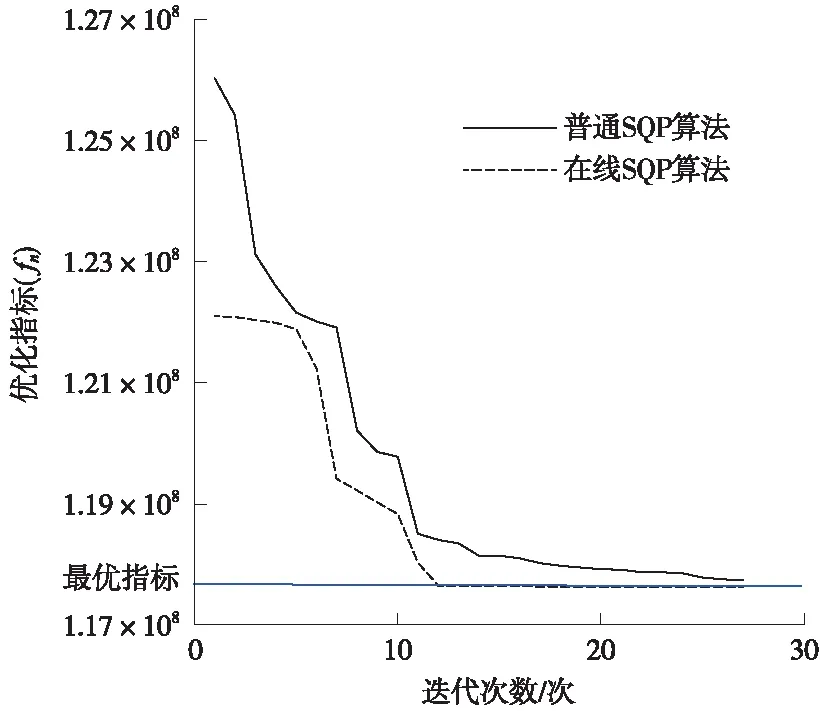
图6 SQP算法收敛情况

结果显示，普通SQP算法在迭代25次左右收敛到最优结果，而在线SQP算法经过12次迭代收敛到最优结果，算法的计算效率有明显提高。

SQP在线控制即在每个决策阶段都执行一次快速SQP算法来实时控制列车的方法，这种控制方式不仅弥补了快速SQP算法在编组误差方面的缺陷，还解决了外界干扰带来的速度偏离问题。

为说明在线SQP控制方法具有良好的抗干扰效果，设计仿真实验：在35 s时刻设置干扰，使列车实际运行速度与理想的编组速度产生偏离；然后，使用在线SQP方法和离线DP方法分别控制列车，得到运行曲线如图7所示。

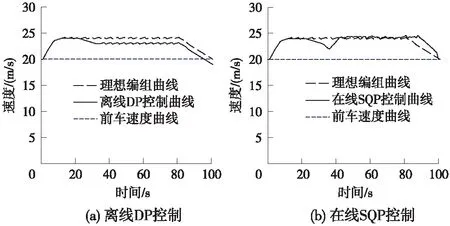
图7 干扰条件下不同控制方法的速度曲线

图7描绘了发生速度偏离后两种控制方法下的后车运行曲线。在发生偏离后，若继续使用离线动态规划控制策略控制列车，列车的运行曲线不会回归到理想的编组曲线，并且在编组结束时刻，速度与目标要求速度相差很大。若使用在线SQP方法控制列车，列车将会立刻调整控制策略，实际运行曲线回归到理想曲线附近，且在结束时刻速度与前车速度相同。

通过图8可以进一步说明在线SQP控制策略的有效性，图8描绘了编组过程中前后列车间距的变化。发生偏离后，动态规划方法控制下，由于后车速度过低，实际间隔与理想间隔差距逐渐拉大，导致在结束时刻两车间距为120 m左右，不满足50 m的理想编组间隔要求；而在线SQP控制下的列车对外界干扰可以作出有效反应，在结束时刻间隔达到50 m左右，达到精确编组的目标。

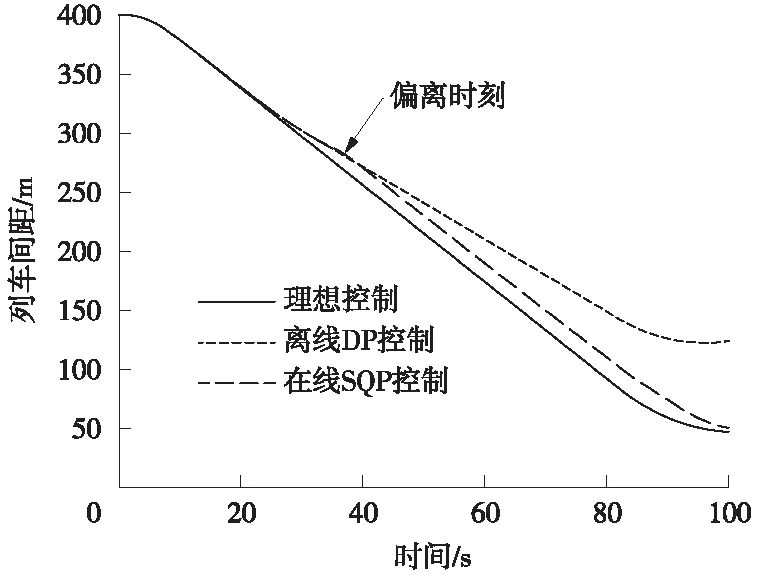
图8 干扰条件下不同控制方法的列车间隔

5 结论

针对动态编组多目标控制问题，提出一种优化控制方法。该方法将动态规划算法和序列二次规划算法相结合，在保证满足多目标控制需求的同时，提高了收敛速度，实现了列车动态编组过程的在线控制。在理想状态下，所提出的动态规划方法在能耗方面较其他有效的优化方法降低了5.6%，在编组精确性方面也具有明显优势；将动态规划结果作为初始解后，提高了SQP算法成功收敛到最优结果的概率，并且将计算时间降低至1 s以内，极大提高了计算效率。在有外界干扰的编组过程中，所提出的在线控制方法以快速SQP算法为基础，平衡了计算效率和优化结果的质量，实现实时计算最优控制策略控制列车，纠正了干扰产生的速度偏离。结果验证了本文方法在动态编组多目标优化控制过程中的有效性。