基于改进型NSGAII的织造车间多目标大规模动态调度
沈春娅, 雷钧杰, 汝 欣, 彭来湖, 胡旭东
(1. 浙江理工大学 机械与自动控制学院, 浙江 杭州 310018; 2. 浙江理工大学 浙江省现代纺织装备技术重点实验室, 浙江 杭州 310018)
《纺织工业发展规划(2016—2020年)》[1]规划中明确指出要推进纺织智能制造,建设纺织强国。在智能制造大背景下,我国纺织业虽然近几年技术进步迅速,但仍属于劳动密集型产业,人力资源成本占比高;同时生产工艺繁杂,品种多样,对生产柔性要求高。纺织业实现智能化生产转型意义重大[1],智能调度在生产过程智能化中具有核心决策功能,是实现纺织智能制造的重要环节。
纺织织造的关键环节是将织轴上的经纱加工为布匹,过程中涉及穿经、织造,每道工序内的设备都为并行机,穿经虽然先于织造,但是织轴是否需要穿经却取决于织造中选择生产的织机,因此,这是一种混合流水车间逆工序调度问题(HFSPI)。HFSPI多目标优化是一类NP-hard难题,已有研究中通过将最早完工时间最小、总拖期时间最小、能耗最小、机器效率最大等目标相互组合,形成了不同的多目标问题模型。对此已有较多智能优化算法的研究,如三级递阶结构的蚁群算法[2]、模拟退火遗传算法[3]、一种改进的紧致遗传算法与局部指派规则结合的方法[4]、NSGAII_3[5]、EA-MOA[6]、一种带精英策略的多目标免疫克隆选择算法[7]等,但对HFSPI多目标优化的研究较少。
织造调度除考虑织造和穿经之间独特的工序关系、工艺的复杂和资源约束带来的调度困难外,还需考虑其多织机、多织轴、多产品形成的大规模调度问题。对大规模调度,一些学者利用启发规则缩小解空间,或通过贪婪变异算子[5]、多种群进化等方法提高算法搜索的深度和广度,但已有最大仿真规模也无法满足普遍调度规模在300台织机、1 000个织轴的中小型织造企业的需求。
实际织造生产调度过程中存在多源随机动态扰动,易使生产偏离原有计划,甚至原有计划失效,静态调度并不适用。动态调度一般根据工件(或任务)实时所处的加工阶段为其分类[8-9],然后确定可以被重新调度的工件。动态调度机制主要有事件驱动、周期性驱动及混合驱动[10],但这些调度机制可适应的场景有限,无法应对复杂的织造生产现场。
目前,针对织造车间这种大规模多目标的HFSPI研究较少,虽有学者研究过织造的织轴调度,但是只考虑了织造工序,并未考虑穿经与织造间的双向约束关系,且实验调度规模也未达到普通生产规模。鉴于此,本文从织造大规模调度出发,研究织造和穿经之间独特的逆工序调度关系,构建织造大规模多目标排产模型,提出一种融合改进优先分配规则、自适应贪婪算子的NSGAII织造车间动态调度算法,以期解决传统动态调度机制在织造插单、打样等复杂生产场景中适应性不强的问题。
1 问题描述及建模
1.1 问题描述
织造车间的生产流程如图1所示。织造车间输入原料是织轴,输出产品为布匹。生产涉及设备包括织机、穿经机和结经机,工序包括穿经、结经、换轴和织造。

图1 织造车间工艺流程Fig.1 Process flow of weaving workshop
按照工序流程进入织造车间的织轴,若需穿经就必先占有一定数量的钢筘,并选择一台穿经机进行穿经,最后选择一台织机完成换轴和织造,若不需穿经,则选择一台织机完成结经和织造。结经机数量充足,其可能带来的约束本文不予考虑。
虽然穿经工序在织造工序的前面,但是否需要穿经取决于织轴织造时织机的选择,若织轴与织机上织轴不属于同一品种,即不满足结经的工艺要求,就必须先完成穿经工序,反之可以选择相对简单快捷的结经工序;工艺上由于织造过程中有的经纱会随机变换位置,同一织机连续多次结经会使经纱相互扭绞,另外综、筘、经停片也需要修理或更换,因此,一般3次结经后改用一次穿经的工艺解决此问题[11],即同一台织机连续3次结经后必须穿插穿经工序。同时钢筘的数量有限,直接约束穿经的进行,进而影响织造。综上可见,织造车间的调度问题相比其他行业要更加复杂,既需要考虑织造和穿经之间独特的工序关系,还要时刻关注钢筘资源带来的约束,所以织造车间的调度问题是带有资源约束的HFSPI。
织造车间除工序间的特殊关系、工艺的复杂和资源约束带来的调度困难之外,织造行业多设备、多任务形成的调度规模之大也要远远超过其他行业,增加了调度难度。
1.2 基本定义与假设
为量化织造车间调度中的各类因素,简化车间内任务、机器和资源的调度,本文做出以下合理的定义与假设。
1) 有n个相互独立的织轴,单个织轴不再拆分,织轴编号i= 1,2,…,n;织轴具有所属订单、品种、绕长、经纱根数等属性。
2) 若织轴品种与匹配织机原织轴品种相同,且织机连续结经次数小于3时就可在织机上结经,结经时间与织轴经纱根数有关;否则必须使用穿经机穿经。
3) 有m台功能相同的织机,编号z= 1,2,…,m;所有织轴都可在织机上生产。织造前穿经的织轴需在织机上先进行换轴,不需要穿经的则在织机上进行结经。换轴时间为定值,一般换轴时间大于结经时间。加工时1台织机同一时刻只能加工1个织轴,加工时间与机器的转速、织轴绕长和纬密有关。
4) 有q台功能相同的穿经机,编号c= 1,2,…,q;穿经机可对所有织轴进行加工。加工时1台穿经机同一时刻只能加工1个织轴,加工时间与机器速度和织轴经纱根数有关;可用钢筘数量必须要满足穿经需要。
5) 有g个相同的钢筘,钢筘是一种互斥资源。织轴穿经时需要占用一定数量的钢筘,同时织机换轴后会释放原织轴的钢筘。穿经时未被占用的钢筘数量应满足穿经需要,否则需进行等待。
6) 零时刻,所有工件均处于待加工状态,所有机器均处于初始空闲状态,进入各织机的第1个织轴需要穿经,钢筘数量为织机数量的1.5倍。
1.3 问题建模
1.3.1 目标函数
为应对织造车间调度的需要,实现各需求间的相互平衡,本文为织造车间调度模型设置了3个目标。
1.3.1.1最小化逾期损失 随着产业链各企业间的联系日益紧密,按时完成生产变得越来越重要,但生产旺季时订单集中到来,订单量在某些时间会超过最大产能,逾期往往在所难免,所以如何让逾期带来的损失最小逐渐成为调度的一个重点。企业往往会根据客户和订单的重要程度给织轴任务赋予不同的权重,但实际生产时很容易忽视权重低的任务。本文为更好反映逾期损失与逾期时间的关系,构建了以任务权重为底数,逾期时间为指数的指数关系模型。图2示出权重hi为1.3、1.5、1.7和1.9时逾期时间与损失之间的关系。可知,相同的逾期时间,权重越高的任务损失越大,同时权重较低的任务如果逾期过多,损失也会指数级增长,因此,该模型既可以很好地关注权重较高的任务,也不会因为任务的权重低而将其忽视。相比文献[12]中客户满意度与交期关系中简单的线性变化,指数模型更能体现企业损失(或客户满意度)与逾期之间的关系。
式中:f1为最小化逾期损失;xi为织轴i的逾期时间,h;Ci为织轴i的织造完工时间,h;di为织轴i的截止时间,h;hi为织轴i的逾期损失权重,是大于1的实数。

图2 逾期时间与损失的关系Fig.2 Relationship between overdue time and loss
1.3.1.2最小化完工时间 最小化完工时间(f2)是大多数调度算法都会确定的目标,也可宏观反映生产的状况,随着生产管理的精细化,车间需要更加具体的调度指标,因此,本文针对织造车间提出了最小化织机空闲时间的目标。
1.3.1.3最小化织机空闲时间 织机是织造车间数量最多、管理最困难的机器,最小化织机空闲时间(f3) 可更加精细地对织机的运行进行优化,提高织机整体效率,减少换轴和穿经工序的次数。

1.3.2 约束条件
织造车间调度问题既要考虑穿结经和织造工序间的约束关系,还要加入钢筘资源的约束,为此建立3个约束条件。
1.3.2.1织造约束 对于要先后在同一台织机上加工的织轴i和i+1:

1.3.2.2穿经约束 对于要先后在同一台穿经机上加工的织轴i和i+1:

1.3.2.3钢筘约束 任意时刻,钢筘的总数量g要不小于正在穿经织轴集JC、已穿经但未织造织轴集JCC和正在织造织轴集JZ所占用钢筘的数量之和,即:
g≥JC+JCC+JZ
2 动态调度
实际生产中因为插单、故障、交货期改变等各种不确定因素,导致实际生产偏离原有计划,甚至原有计划失效,因此,根据实际情况动态的调整计划是非常必要的。
2.1 动态调度窗口
实现动态调度首先要标注织轴的处理状态,确定动态调度窗口,即可调度织轴集JS。本文将所有织轴分成未加工织轴集JU、正在穿经织轴集JC、已穿经但未织造织轴集JCC、正在织造织轴集JZ和已织造织轴集JZC。调度开始前,根据织轴状态将织轴集JU、JC和JCC作为动态可调度织轴集JS,实时更新机器动态信息和钢筘信息。调度时,将JS中的织轴按逾期损失最小、最大完工时间最小和织机空闲时间最小的多目标从全局出发进行调度。
2.2 基于支配关系评价的动态调度机制
目前,针对车间的动态调度机制主要分为事件驱动、周期性驱动和事件与周期性混合驱动3种。事件驱动机制为及时应对车间生产加工过程中的突发事件,当设定事件发生时就进行调度;周期性驱动机制是确定1个时间周期进行调度;事件与周期性混合驱动的机制是前二者的融合,综合了前二者的优点。这些调度机制是根据不同的应用场景提出的,也各有优缺点,但这些调度机制都缺少量化的评价机制来衡量是否需要调度,因此,本文提出了基于支配关系评价的动态调度机制。
当一些突发或周期性事件导致实际生产偏离原有计划时,根据原方案的调度计划可计算出f1、f2、f3这3个目标函数值,同时调度系统也会生产新的Pareto调度方案解集。若新解集存在新方案的目标值f′1、f′2、f′3,若原方案目标函数fi与新方案目标函数f′i满足支配关系公式:
则新方案优于旧方案,新方案可取代旧方案。
为使该评价可满足调度要求,本文做出以下合理的设定:当系统初次调度时原方案不存在或有新织轴插入,使得原方案不再适用时,则令旧方案的fi为无容大,让新旧方案目标值必然满足支配关系公式。图3示出动态调度程序框图。

图3 动态调度流程图Fig.3 Dynamic scheduling flow chart
3 改进的NSGAII调度算法设计
遗传算法是一类借鉴生物界自然选择和自然遗传机制的高度并行、随机、自适应的搜索算法,被广泛应用于函数优化、组合优化、生产调度、机器学习等[13]。NSGAII作为一种多目标遗传算法[14],其基于Pareto支配关系的排序方式降低了非劣排序复杂性,运行速度快,解集收敛性好,但解空间过大时易陷入局部最优。启发式规则(启发式算法)是一种基于直观或经验构造的算法,合理的构造可有效减小算法搜索空间。本文为解决搜索失灵问题,将遗传算法与启发式规则融合。
3.1 基于决策变量的调度规模分析
根据上述问题描述及模型,实现织造调度共要求解4组决策变量,分别是织轴进入织造工序的顺序、织轴对织机的选择、织轴进入穿经的顺序和穿经机的选择。
参考浙江某小型织造车间的数据为例:100台织机,2台穿经机,300个织轴的织造车间调度规模下,全部织轴进入织造工序的顺序有300!种可能;若每个织轴可选任一织机,共有100300种可能;假设20%织轴需要穿经,则织轴的穿经顺序有60!种选择;穿经机选择有260种,此时完整解空间中可行解个数为300!×100300×60!×260= 2.94×101 314。遗传算法按照种群规模100,最大迭代次数为500计算,算法最多能评价到的解为50 000个,此时算法能评价到的解和完整解空间已经不成比例,搜索宛如大海捞针,遗传算法很难在有限的时间内在如此巨大的空间中进化出高质量解,且极易陷入局部最优,本文称这种现象为搜索失灵。
随着调度规模的增大,解空间呈指数级膨胀,这也是遗传算法在小规模调度中的效果良好,大规模调度中求解能力迅速下降的原因。文献[5-6]也注意到了这个问题,并通过缩小解空间、增大算法评价范围、利用启发式规则引导算法搜索等来进行克服,但实现的规模远没有达到本案例的需求。
3.2 求解决策变量的启发式规则
为缩小解空间,本文针对不同的决策变量设计了相应启发算法。考虑织造车间中织机选择对穿经工序的逆影响,且调度关键工艺主要在织造工序上,因此,将织轴与织机的匹配选择作为核心决策变量,提供2种启发式规则,以每个织轴的织机选择规则作为染色体基因进行编解码,然后再利用遗传算法对启发规则的选择进行全局优化;将织轴进入织造工序的顺序、织轴进入穿经的顺序和穿经机选择作为非核心决策变量,采用单一的启发式规则。
3.2.1 织机选择启发规则
依据织轴匹配织机的实际需求,提炼出3个织机排产特征:最早可用时间、是否需要穿经和织速,然后根据特征的优先级为织轴选择织机。本文设计了a、b2个规则。
规则a:按照最早可用时间较小>无需穿经>织速较快的优先级顺序为织轴选择匹配织机,即优先选择最早可用时间最小的织机,最早可用时间相同时优先选择无需穿经的织机,若前2个条件仍无法匹配到织机,则优先选择织速最快的织机。
规则b:按照无需穿经>最早可用时间较小>织速较快的优先级顺序选择匹配织机,即优先选择无需穿经的织机,在无需穿经的织机中优先选择最早可用时间最小的织机,最早可用时间相同时,则优先选择织速最快的织机。
3.2.2 织造排序的启发式规则
基于最早截止时间优先(EDF),将可调度织轴集JS中的织轴按其截止时间从小到大进行排序,优先选择截止时间小的,在截止时间相同时按照织轴到达时间排序。
3.2.3 穿经排序启发规则
根据织造排序和织机选择的决策变量可确定哪些织轴需要穿经和其织造的开始时间,将织造工序的开始时间作为穿经工序的截止时间,基于EDF按照穿经工序的截止时间从小到大排序,优先选择截止时间小的,截止时间相同时以织轴到达时间排序;钢筘的占用优先级也服从此排序。
3.2.4 穿经机选择启发规则
穿经机的选择则在排序的基础上,将织轴优先分配到最早可用时间最小的穿经机上。
3.3 启发规则的染色体编解码
核心决策变量织机选择的启发规则有a、b2种, 对规则选择进行编码求解,本文采用实整数编码,是实质编码的一种,其编码的染色体不需要解码即可直接表示对应的决策变量。染色体个体可用一维矩阵表示为 [x1,…,xi,…,xn],染色体长度为可调度织轴集JS中织轴的个数,xi的值对应启发式规则的编号。例如某个体染色体矩阵为 [0,1,1,0,1] 时,表示排序后对应的织轴分别按照 [a,b,b,a,b] 的启发规则匹配选择对应特征的织机。
这样任意织轴的调度路线只有2种可选,根据3.1节中的案例,全部织轴共有2300种调度可能,即使织机数量增加,也不会使解空间增大,解空间仅与织轴个数呈指数关系。按照本文这种方法将遗传算法与启发式规则融合,前者负责全局优化,后者负责具体任务的调度,在保障算法优化质量的同时,极大缩小遗传算法的搜索范围,提高搜索效率,但本文这种编码方式不能表达完整的解空间。
3.4 自适应贪婪进化算子
NSGAII随着进化代数的增加,种群个体的相似度可能逐渐增加,进而陷入局部最优,而且NSGAII缺乏局部深入搜索的能力。为此,本文提出了自适应贪婪进化算子,其并非独立存在,是一个贯穿种群进化始终的框架,该算法主要通过检查子代中是否有新精英个体出现,用循环来推进算法更加深入的搜索,以此防止进化陷入局部最优。为避免某一代过度贪婪循环,设置了贪婪循环的次数上限igreed,同时为避免全局的过度贪婪搜索,设置了连续无效贪婪代数的上限jgen。
贪婪算子在算法中的全局搜索过程步骤如下。
步骤1:以父代种群P(t)为基础进行进化操作,并通过局部贪婪搜索获得新子代D(t),若局部贪婪搜索为无效进化,则进入步骤2,否则进入步骤3。
步骤2:连续无效贪婪次数j加1,若j未超过设定最大次数jgen,进入步骤1;若j超过jgen,则退出贪婪算子,不再进入。
步骤3:父代种群P(t)和子代种群D(t)合并获得混合种群R(t),通过NSGAII算法的快速非支配排序分层及个体拥挤距离的计算,从R(t)中选择合适个体生成下一代父种群P(t+1),种群规模和前一代一致。种群迭代次数i加1,并返回步骤1。
贪婪算子的局部搜索过程步骤如下。
步骤1:以父代种群P(t)为基础进行选择、交叉、变异获得新子代D(t)。
步骤2:实现对某一代的贪婪搜索,将父代种群P(t)与子代种群D(t)进行对比,若∃Xa∈D(t),对Xb∈P(t),使Xa>Xb或Xa、Xb互不匹配,则记为有效进化进入步骤4;否则记为无效进化,进入步骤3。
步骤3:贪婪搜索次数i加1,若i未超过设定最大循环次数igreed,进入步骤1;若i超过igreed仍未实现有效进化,记为无效贪婪,放弃本代的贪婪循环进入步骤4。
步骤4:将父代种群P(t)与子代种群D(t)合并生成R(t),本代搜索结束。本文使用的选择、交叉和变异算子分别为:二元锦标赛选择策略[15]、模拟二进制交叉[16]和多项式变异算子[17]。
4 仿真与分析
为验证织造车间调度模型及其求解算法,本文在参考浙江兰溪某纺织企业数据的基础上,编写案例参数。其中,m表示织机数,k表示订单数,每个订单的权重为[1,2]间的任一小数,各订单的到达时间均设为0,截止时间满足ceil(7/m)×500 本文使用Python编程,用到的开源程序包主要有geatpy、numpy、matplotlib。计算机操作系统为64位 win7,内存16 GB,处理器主频2.90 GHz。 为验证本文贪婪进化算子对算法搜索能力的提升,将NSGAII与带自适应的贪婪进化算子的NSGAII(NSGAII_G)进行对比,比较二者Pareto 前沿解集的收敛性。在控制变量、编解码方式,选择算子、交叉算子和变异算子等均相同条件下,按照参数生成规则,并令m=12,k=10,种群规模Popsize为100,最大迭代次数maxGen为300,交叉概率Pc=1,变异概率Pm=1/n(n为织轴个数),igreed=5,jgen=5,随机生成a、b、c、d 4个调度仿真案例,每个案例分别进行 4次仿真。 图4分别示出NSGAII和NSGAII_G的a、b、c、d的4个案例仿真结果的Pareto前沿解集分布对比图。3个目标函数f1、f2、f3越小越好。图中NSGAII_G的Pareto前沿点主要分布在NSGAII的左下侧,可知,NSGAII_G的前沿点的各目标值相对更小,支配能力更强。同时用C指标[18]对结果量化分析,结果如表1所示。可知,C(NSGAII,NSGAII_G)< C(NSGAII_G,NSGAII),即NSGAII_G的Pareto解集收敛性更好。 近视算法[19-20]是按启发规则调度的算法;NSGAII_3是求解多目标混合流水车间调度的改进NSGAII,因为原算法与本文的应用场景存在差异,本文在使用时均做了适当修改,主要还原其算法思路。 多目标算法所得结果为一个包含多个个体的Pareto最优解集,解集中所有个体均互不支配。为方便多目标算法与近视算法的比较,本文根据织造车间的实际需求,在解集中按照f1逾期损失>f2最大完工时>f3织机空闲时间的优先级顺序选出“最优个体”,即优先选择逾期损失最小的个体,逾期损失相同时优先选择完工时间最短的,完工时间相同时优先选择织机空闲时间最小的。 图4 前沿解集分布Fig.4 Frontier solution set distribution.(a)Case a; (b)Case b; (c)Case c;(d)Case d 表1 C指标结果对比Tab.1 Comparison of C index results 将近视算法、本文设计的融合启发规则并带自适应贪婪算子的NSGAII(H-NSGAII_G)和NSGAII_3 的调度结果进行对比。按照参数生成规则,分别令m=6、k=12,m=100、k=200和m=500、k=600 生成a1、b1、c13组不同规模的调度案例。仿真时选取不同数量的织机和织轴,算法参数设置同4.1节,结果如表2所示。 表2 3种算法的实验结果统计Tab.2 Three algorithms of experimental results statistics 从表2中各目标值的仿真结果可知,a1组中织机数量较少时,当织轴数n为14、28时,NSGAII_3最优,H-NSGAII_G次之;当n为42时,H-NSGAII_G最优,NSGAII_3次之;当n为56、70时,H-NSGAII_G最优,近视算法次之。可见织轴数较少时,解空间还较小,此时拥有较完整解空间的NSGAII_3可以找到更优的解;但随着织轴增多,解空间增大,NSGAII_3的搜索空间快速扩大搜索能力开始下降,H-NSGAII_G的能力开始展现。 b1组中,织机数量为100,虽然NSGAII_3含有启发式规则的辅助引导,但由于搜索空间膨胀,已出现本文3.1节中描述的搜索失灵现象,表现极差。n为245时,近视算法与H-NSGAII_G在f1和f2上还各有优势,但随着织轴数量增加,在f1、f2和f3上H-NSGAII_G均优于或等于近似算法和NSGAII_3。相比近似算法,当n=490、735、980、1 225时,完工时间分别减少11、26、54、30 h。 在c1组中织机为500台,织轴有4 000个,其已达到中小型的织造车间的规模。H-NSGAII_G调度结果远优于近视算法和NSGAII_3,相比近视算法可节省完工时间626 h,这主要是因为H-NSGAII_G全局优化能力较强,而近视算法只是符合一般经验的调度规则,因此,规模越大情况越复杂,H-NSGAII_G 的优化能力就越突出。 从表2可见:近视算法在计算耗时上始终保持较高优势;H-NSGAII_G与NSGAII_3的耗时会随调度规模增大快速增加,特别是在c1组的大规模调度中,H-NSGAII_G调度耗时约为6.4 h,近视算法仅为22.24 s,但考虑到H-NSGAII_G节省完工时间626 h,H-NSGAII_G仍有较大的优势。 图5 织造工序再调度甘特图Fig.5 Weaving process is rescheduled Gantt chart 紧急插单是织造生产时常见的需动态调度的事件,本文以此来验证动态调度可行性。根据参数生成规则,令m=6,k=4时,案例调度结果见表3。其中15号到16号织轴的开始时刻跨度变大是因为钢筘资源有限,16号织轴需等待钢筘资源释放后才能开始穿经。 表3 穿经工序调度Tab.3 Drawing-in process scheduling 在时间为200 h时出现一个紧急订单,订单到达时间为200 h,截止时间为900 h,生产5号品种,4个织轴编号分别为71、72、73、74,织轴经纱绕长为 2 500 m, 经纱根数为8 500根。根据3.2节的动态调度机制重排后结果见表3,再调度部分见图5。图5 中浅色条块表示织机处于运行状态,深色表示空闲,其上的数字表示任务编号及品种,如“8(5)”表示 8号织轴5号品种。 表3中,时间为200 h时初始调度中只有29号织轴未开始穿经,再调度后紧急订单中的71号织轴先于29号加工,29号织轴拥有了新穿经计划,新增了 20号, 21号等在初始调度中不需要穿经的织轴。图5 中2号织机在4号织轴与71号织轴间存在较长的空闲时间,是因为钢筘资源对71号织轴的穿经约束造成的,重调度后逾期损失为0,可见紧急订单被很好的插入生成计划。 根据本文2.1节中的动态调度规则,本次再调度的实际只为时间200 h时还未开始的21个任务进程,已完工或正在生产的任务不参与再调度。整体调度耗时/织轴任务数=单个织轴调度耗时,根据表2 H-NSGAII_G 的单织轴调度理论耗时约5 s,本次再调度理论耗时约105 s,实际运行H-NSGAII_G再调度耗时102.5 s,可见临时紧急任务的插入并未对算法耗时产生影响。 本文针对多织机、多织轴、多产品的大规模织造调度,且织造和穿经工序之间存在逆工序调度关系,已有的启发式算法优化搜索效率低的问题,在综合考虑穿经约束下,以完工时间、订单逾期、织机空闲时间为优化目标构建了织造多目标大规模排产模型;提出了一种大规模动态调度的改进NSGAII 遗传算法,为适应织造调度模型的特点,设计了一种改进启发规则的编解码方式,极大缩小了解空间,解决已有优化方法在织造工序大规模调度寻优中时间长,易陷入局部最优的问题。设计了一种基于支配关系评价的动态调度机制,通过实验验证了策略的有效性,解决传统调度优化方法在织造实际应用中响应机制较差的问题。 本文在解决大规模调度问题上,实际是利用启发式规则对完整解空间进行切割,遗传算法在其中起着全局指挥的角色,虽然剔除了大量质量较差解,但也会失去一些优秀的解,而且算法在处理大规模调度时计算耗时较长,这些问题还有待解决。4.1 贪婪进化算子的有效性验证
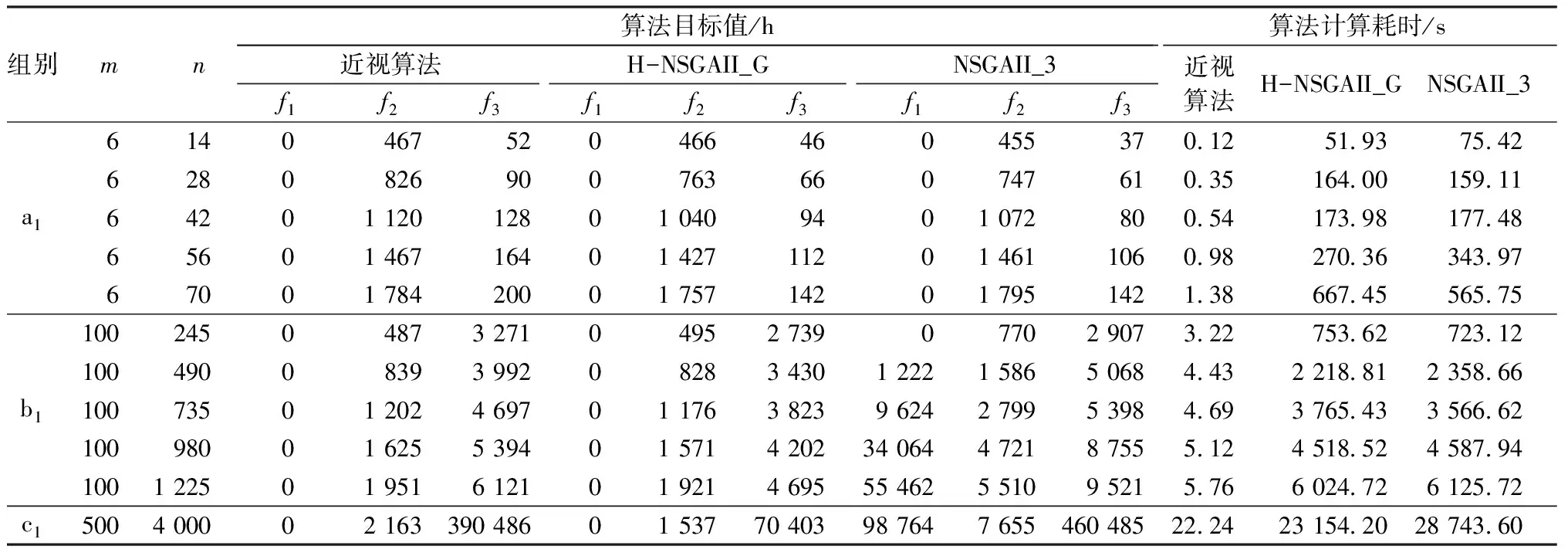
4.2 与已有算法静态调度仿真对比



4.3 动态调度可行性验证

5 结 论

