基于敏感度分析方法的拱状橡胶三向隔震支座竖向刚度研究

吴时程 盛 鹰 刘 彤 贾 彬 王汝恒

(1. 西南科技大学土木工程与建筑学院 四川绵阳 621010； 2. 中国工程物理研究院 四川绵阳 621900)

地震是一种突发性强、破坏力大的自然灾害，不仅威胁着人类的生命，也对人类文明、文化财富造成了不可逆转的损失。我国的南北地震带具有很强的活跃性，是我国地震的主要发生地和主要受灾地区。该地震带上云贵川等地有着大量可移动文物，很容易因遭受地震灾害而毁损[1]。地震灾害对文物的展示和保存造成了威胁。目前，建筑的减隔震技术已经趋于成熟，文物隔震保护也从中获得了启发，例如滚轮式[2]等机械式隔震装置和橡胶等变形式隔震装置对文物陈列柜具有隔震保护作用。

由于文物本身具有不同的特性[3]，使得文物隔震装置的应用仍需要不断改进。机械式隔震装置虽具有较好的水平隔震性能[4]，但其构造复杂、造价高且对于体积大、质量大的隔震对象具有一定的局限性;变形式隔震装置在建筑结构中具有广泛的应用，特别是橡胶支座在建筑基础和桥梁中的减隔震效果突出[5-6]。相对于建筑橡胶隔震支座来说，文物隔震橡胶支座对竖向承载力的要求较低且对橡胶水平变形限制较小，在保证稳定性的基础上提升橡胶的水平变形能力，文物橡胶隔震支座就能够更好地发挥隔震性能。通过对橡胶镂空处理形成圆拱结构，减小其水平刚度，提高橡胶水平向变形能力，延长其结构的自振周期，改变其动力特性从而避开地震波的危险频段。同时，橡胶的大变形在材料自身的阻尼作用下能够消耗更多的能量。并且，拱状结构能够提高竖向承载能力，内部的空腔结构能够形成“弹簧”作用，减小上部结构对地震力的响应。Engelen等[7]通过对橡胶挖孔调整支座的水平刚度及耗能特性，但几何修改同时也会影响竖向刚度及其承载力；文献[8]研究表明，减小水平刚度从而增大橡胶水平变形能力，可充分发挥出橡胶的隔震性能；文献[9]指出，竖向刚度是影响橡胶支座的稳定性与竖向设计承载力的因素之一；文献[10]研究表明，橡胶支座的稳定性与水平变形和竖向压应力限值有关，水平刚度受竖向荷载的影响。因此，橡胶支座竖向刚度不仅决定了其竖向承载能力，同时还与支座的隔震性能密切相关。拱状橡胶三向隔震支座的形状是基于半球状橡胶拱状镂空形成的，内部的空腔能够减小支座的水平刚度。由于拱状橡胶三向隔震支座橡胶的形状较为复杂，为了方便竖向刚度的调整，探究装置内部橡胶尺寸对竖向刚度的影响有利于提高装置的适用范围和隔震性能。

1 隔震装置竖向压缩刚度试验

1.1 支座影响因素分析

目前针对文物的橡胶隔震器较少，建筑上使用的橡胶隔震器在承载力和位移要求设计方面有较高要求，不能完全适用于文物隔震。文物隔震器的上部荷载相对于建筑隔震器来说要小得多，并且容许的水平位移量相对于建筑隔震也较大，这就意味着文物隔震橡胶能够通过较小的水平刚度来达到隔震的目的。拱状橡胶三向隔震支座如图1所示，以类半球橡胶为主体,在橡胶内部进行两个拱状截面的环向镂空，形成一个半球形圆拱。拱状的结构设计可以阻断、隔离震源，达到良好的减震效果，同时能均匀分散所承受的压力和振动冲击力，钢套筒能够传递力使橡胶内部变形，充分发挥橡胶的性能。

图1 拱状橡胶三向隔震装置图Fig.1 Arched rubber three-way seismic isolation device

建筑隔震橡胶支座形状系数是影响橡胶支座性能的重要几何参数，将橡胶支座的尺寸变化反馈成形状系数进而对橡胶支座的承载力和变形能力进行数学描述。第一形状系数S1定义为橡胶支座中各层橡胶层的有效承压面积与其自由表面积之比[11]，即：

(1)

式中：S1为第一形状系数；d为外径；d0为内径；tr为单层橡胶厚度。第二形状系数S2定义为橡胶支座有效承压体的直径与橡胶总厚度之比，即：

(2)

式中：S2为第二形状系数；n为橡胶层数。S1表征橡胶支座中钢板对于橡胶层变形的约束程度，根据橡胶支座竖向刚度计算公式[12]，S1值越大，橡胶支座的受压承载力越大，竖向刚度越大。

(3)

式中：Kv为竖向刚度；A为受压面积；E∞为橡胶的体积弹性模量；E0为橡胶的弹性模量；κ为刚度系数；Tr为橡胶总厚度。建筑隔震橡胶中竖向刚度与橡胶弹性模量和几何尺寸有关，在材料属性不变的情况下，第一形状系数对于竖向刚度的影响较大[13]。第一形状系数是单层橡胶的有效承压面积与其自由表面积之比，两者的大小取决于支座整体尺寸和开孔大小。普通橡胶支座中部的镂空体积是橡胶支座竖向刚度的主要影响因素之一，而拱状橡胶三向隔震支座其主要的形状就是对橡胶内部进行镂空处理，镂空部分的形状和体积是其竖向刚度的影响因素。由于该支座为旋转体，采用截面等效体积的方式对支座的截面进行镂空体积的研究。在整体尺寸和橡胶属性不改变的情况下，橡胶内部的镂空部分是其竖向刚度主要的影响因素。为了更好地对该支座的竖向刚度进行研究，对镂空部分截面进行简化,定义4个形状尺寸参数h1，h2，l，r为装置竖向刚度的主要影响因素，如图2所示。

图2 隔震装置镂空部分尺寸参数示意图Fig.2 Schematic diagram of the dimension parameters of the hollow part of seismic isolation device

1.2 试验概况

本试验采用拱状橡胶三向隔震装置进行试验，试件尺寸参数如表1所示，试件个数为4个。试验加载装置采用DBSL-30t万测试验机，加载精度为1/1000。加载速率对于橡胶支座力学性能实验具有一定的影响[14]。由于该橡胶支座不属于常见类型，不能够参照规范中的加载速率进行实验，在进行试验时应当首先探究加载速率对实验结果的影响，保证试验结果的真实性。设定加载速率为 0.5，1.0，3.0 mm/min(位移控制)，比较实验结果。加载方式为0→Y→Y/2→Y→Y/2→Y→0，加载目标为Y=6 mm，仅进行竖向加载。由于过大的竖向变形会使得镂空橡胶中部与下部钢板接触，使其拱状结构受力形式改变，因此在竖向容许位移为11 mm的基体上，预留 5 mm变形储备，设定最大加载位移为 6 mm。

表1 支座参数Table 1 Bearing parameters

1.3 试验结果及分析

对拱状橡胶三向隔震装置进行纯压下的竖向刚度试验研究，加载位移达到6 mm时，不同加载速率对结果的影响如表2所示，支座竖向荷载与竖向位移之间的关系如图3所示。从图3可以看出，采用3种不同的加载速率对4号试件进行实验，3次加载关系曲线基本重合，反映了相同的变化规律。表2中3次加载的最大压力的最大误差为3.3%，表明加载速率对该橡胶支座竖向压缩实验的影响可忽略不计，这有利于保证后续试验的准确性，同时也体现了支座具有稳定的压缩性能。

图3 3种不同加载速度的力-位移曲线Fig.3 Force-displacement curves for three different loading speeds

表2 不同加载速率下最大压力数值Table 2 Maximum pressure values at different loading rates

图4是竖向荷载与竖向位移的关系曲线。从图4可知，试件的竖向荷载和竖向位移的关系曲线规律相同，在往复3次的加载中关系曲线基本重合，第1次往复中曲线虽有一些偏移但是试验结果趋势相同为正常现象。在4组实验中，1号试件和4号试件的最大竖向荷载结果相近，而2号试件和3号试件在整体结果上有上下浮动，这是由于试件加工过程中顶部钢板偏心和构件之间的连接不密实造成的。考虑支座的加工差异，去除两个偏差较大的值，将两组结果相近的均值作为支座的竖向设计承载力(1 384.89 N)。从图5可以看出，支座在加载过程中未出现破坏，并且在卸载过后支座能够恢复原状，说明该支座具有很好的复位性能和竖向承载力。

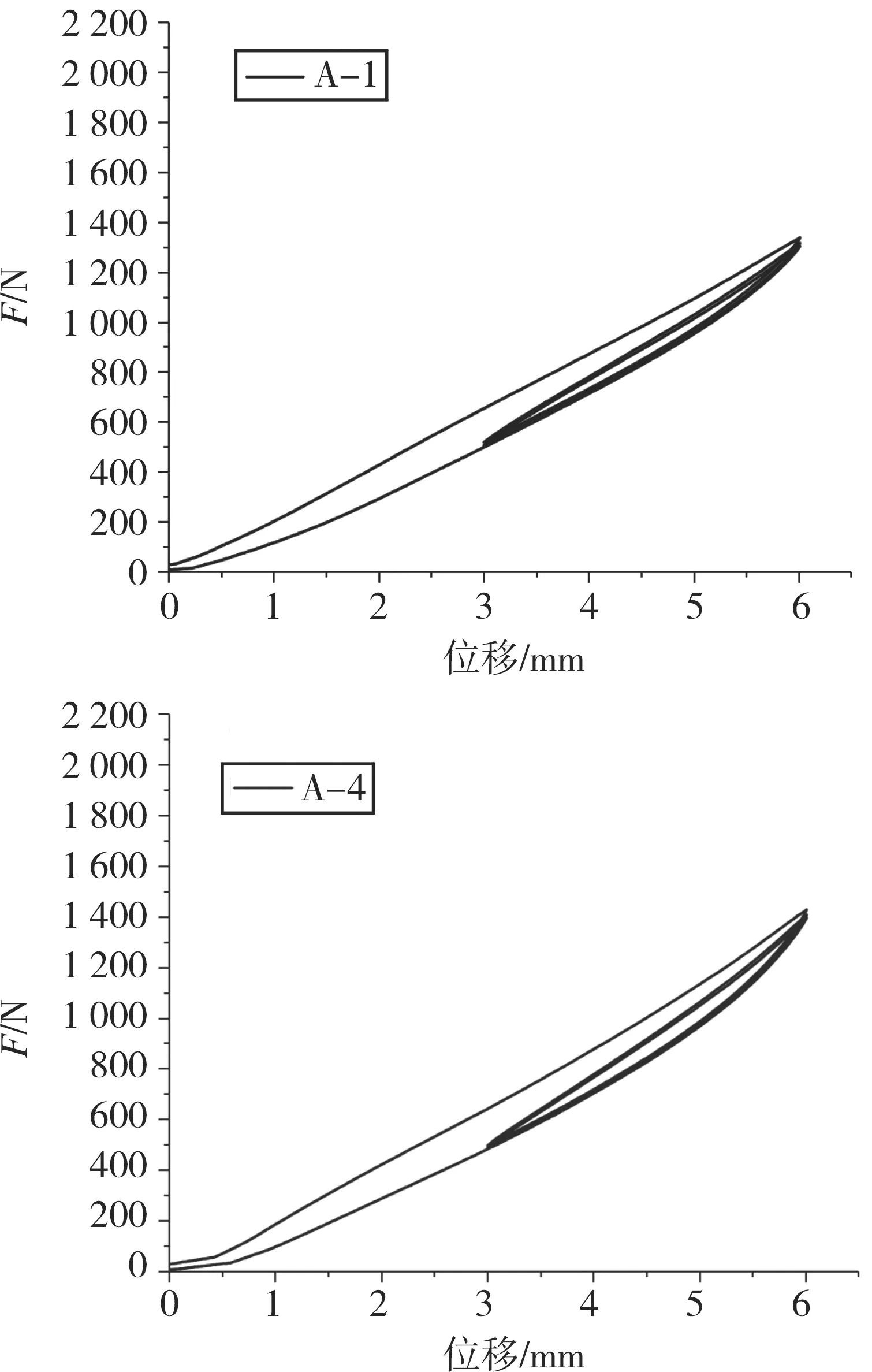
图4 竖向荷载-竖向位移关系曲线Fig.4 Vertical load-vertical displacement relationship curves

图5 未加载(左)与加载至6 mm(右)对比图Fig.5 Comparison of unloaded (left) and loaded to 6mm (right)

图6是隔震支座竖向刚度-压应力关系曲线。从图6可以看出，试件在0 kPa到25 kPa加载时，随着压应力不断增大，竖向刚度有明显增大，这是由于支座在加载前钢板的找平过程和各个构件之间的连接空隙被压实，使得竖向刚度大幅度增加，因此可认为该支座需要达到一定的竖向载荷才能够发挥其性能。当竖向压应力增加到25 kPa以上时，随着竖向压应力的增大竖向刚度的变化较小，在达到6 mm最大位移荷载时，平缓阶段最大的竖向刚度为238.37 N/mm，最小竖向刚度为210.9 N/mm，平均竖向刚度为217.74 N/mm，竖向刚度的变化范围在0.12%～7.80% 之间，可认为该装置的竖向刚度在一定范围内受压应力的影响较小，具有很好的稳定性。试验过程中的竖向刚度平缓段的均值为该装置的竖向刚度。

图6 竖向刚度-压应力关系曲线Fig.6 Vertical stiffness-compressive stress relationship curves

2 尺寸参数对支座竖向刚度的影响分析

通过试验得到了设计尺寸下拱状橡胶支座的刚度。由于该装置构造不同于建筑所用的橡胶支座，不能够通过形状系数进行刚度计算。通过试验得到4个尺寸参数(h1，h2，l，r)对竖向刚度的影响所产生的工况较多，因此本文采用多工况的参数化有限元模拟，研究各个尺寸参数对于支座刚度的影响规律。在进行多工况有限元模拟之前通过试验验证模拟结果的可靠性。

2.1 模型可靠性验证

运用有限元分析软件ANSYS对支座的竖向压缩进行模拟。根据装置的实际尺寸进行建模，对需要根据工况进行变动的尺寸进行参数化建模，建立全尺寸三维实体模型。本模拟主要是研究4个尺寸参数对支座竖向刚度的影响，材料模型采用能够很好反映橡胶性能的Mooney-Rivlin材料模型[15]。橡胶的Mooney-Rivlin超弹性材料模型定义材料为不可压缩性，超弹性材料的本构模型一般通过应变能密度函数来定义，如公式(4)所示：

(4)

在ANSYS模拟中，橡胶采用了两参数Mooney-Rivlin材料模型，通过定义C10，C01的值来表征橡胶材料的力学性能。利用橡胶硬度和弹性模量求得C1和C2[16]，其中C1为1.199 3 MPa，C2为0.024 0 MPa；橡胶压缩弹性模量为7.34 MPa；橡胶泊松比为0.489 9；钢材为304号钢。橡胶采用能够反映大变形、大应变特性的8节点Hyper-elastic Solid185单元，钢板采用8节点Solid85单元，最终建成的拱状橡胶三向隔震装置的三维实体模型如图7所示，该模型节点数为113 111，单元数为99 216。

图7 拱状橡胶三向隔震装置有限元模型Fig.7 Finite element model of three-way arched rubber seismic isolation device

利用ANSYS对支座进行竖向压缩数值计算，试验与数值模拟计算结果的竖向刚度对比见表3，试验与模拟结果曲线对比如图8所示。在数值模拟计算中，竖向刚度与竖向位移几乎呈线性增长，与试验结果的趋势相同且较为平稳，在均值处波动范围为 ±6%，得到的平均竖向刚度为230.034 N/mm，试验得到的平均竖向刚度为242.83 N/mm，两者的相对误差为5.27%。虽然两者竖向刚度存在偏差，但是模拟值较小，对于实际使用较为安全，因此可认为该模型具有可靠性。

图8 试验与模拟结果曲线对比图Fig.8 Comparison of test and simulation results

表3 竖向刚度试验值与模拟值对比Table 3 Comparison of test and simulation values of vertical stiffness

2.2 水平剪切性能分析

隔震装置的水平剪切性能是衡量其隔震效能的一个重要因素，基于上一小节装置有限元模型基础，对装置进行水平剪切试验模拟。根据《橡胶支座第1部分：隔震橡胶支座试验方法》GB/T 20688.1—2007可知，在进行水平剪切试验时应当考虑装置高度与水平变形的关系。由于拱状橡胶三向隔震装置具有中部镂空和径高比较小的特点，为了避免装置发生结构性破坏而失效，进行水平剪切的幅值不宜设置过大。因此，模拟工况采用压应力为65 kPa和100 kPa，两组压应力下的竖向刚度都较为稳定，但是受到的荷载为竖向加载的中点和即将到达设置的加载位移处，剪切应变加载至25%。

从图9可以看出，当剪切应变达到25%时，压应力为65 kPa的剪力为4 233.73 N，压应力为100 kPa的剪力为4 285.9 N，差值为1.12%，在两组不同压应力作用下剪力的变化不大，说明在一定范围内剪力受压应力的影响较小，具有稳定的水平变形能力。两组曲线的趋势一致，剪切位移为 0.015 m 时为线性阶段，之后曲线趋于平缓，反映出橡胶超弹性的材料属性，也说明了拱状的结构使得支座获得了更好的水平变形能力。

图9 竖向压应力65 kPa和100 kPa的水平剪切曲线Fig.9 Horizontal shear curves under vertical pressures of 65 kPa and 100 kPa

2.3 竖向刚度敏感度分析

为了探究4个尺寸参数对支座竖向刚度的影响，利用正交设计方法进行多因素影响有限元模拟，通过规格化的正交表进行模拟的工况设计，能够充分考虑各个影响因素的组合影响。为了分析h1，h2，l，r影响因素的敏感性，结合正交试验，将竖向刚度作为评价对象进行显著性分析[17]。通过计算统计参数Kij和极差Rj衡量影响因素的敏感性。

(5)

(6)

假设各参数之间没有影响，考虑h1，h2，l，r4个因素对拱状橡胶三向隔震支座进行正交工况设计，采用3个因素水平，参数取值和因素水平取值如表4所示。

表4 各参数和水平因素取值Table 4 Values of each parameter and level factor

根据四因素三水平正交试验表L9(34)进行有限元模拟工况设计，采用已验证可靠度的有限元模型进行参数化建模计算，得出各工况拱状橡胶三向隔震支座的竖向刚度如表5所示。三水平下4参数的极差计算结果如表6所示。从数值模拟计算可知，4个尺寸参数对于竖向刚度的影响敏感度为：l>h1>h2>r。竖向刚度KV随着h1,h2的增大而小幅度减小；随r的增大而小幅度增加；随l的增大而明显减小。从参数极差分析来看，4个尺寸参数中l起主要影响作用，其他3个参数的敏感度虽然较小，但是3个参数共同作用下的敏感度也较高。l尺寸参数主要是影响支座拱状橡胶的支撑面大小，h1，h2，r影响的是镂空高度，因此计算该支座竖向刚度需要考虑支撑面和镂空高度的影响。

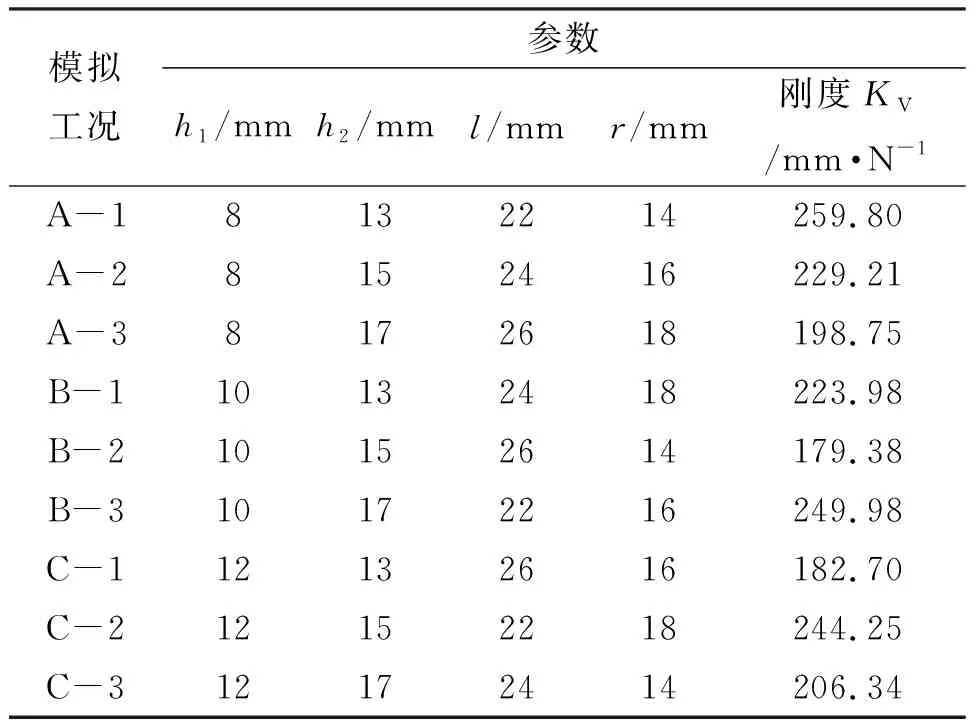
表5 正交设计工况模拟计算结果Table 5 Simulation calculation results of orthogonal design conditions

表6 各参数极差分析Table 6 Range analysis of each parameter

3 竖向刚度计算分析与公式拟合

由敏感度分析可知4个尺寸参数对于竖向刚度的影响大小差异较大，将影响较大的l作为独立因素考虑，将其余影响较小的3个尺寸参数作为整体因素进行考虑，h1和h2与竖向刚度成反比例关系，r则为正比例关系。由于l为主要影响因素，设置11个水平梯度，而整体因素设置5个水平梯度,分别进行l的11个梯度模拟计算，其中的3个参数变化梯度一致，工况设置见表7。这样的工况设计，能够较为直观看出单因素和整体因素各自的变化趋势及两者之间的影响，利于分析两个因素对于竖向刚度的规律及对计算公式的拟合。

表7 拟合样本数据工况

从图10的模拟曲线可看出,曲线的整体趋势基本相同，所反映的影响规律与敏感度分析一致，竖向刚度随着l值的增大明显减小，同一整体因素作用下的竖向刚度下降52.5%～60.8%；竖向刚度随着h1，h2，r整体减小而增大，在同一单因素l的作用下竖向刚度下降了8.0%～11.5%。根据拱状橡胶的形状特性，平面受力分析如图11所示。在上部荷载的作用下，由于拱的传力特性，合力T分解为竖向力Ty和水平力Tx，Ty是作用在支撑面上的分力，

图10 单因素和整体因素作用下竖向刚度模拟值曲线图Fig.10 Curves of simulation values of vertical stiffness under single factor and integral factor

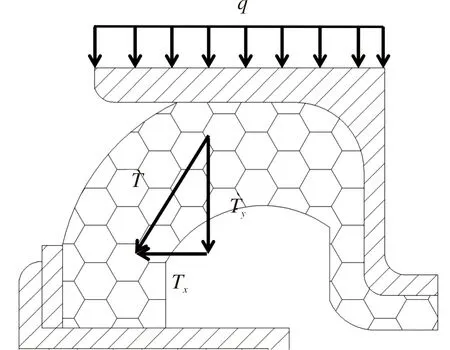
图11 圆拱橡胶平面受力分析Fig.11 Plane stress analysis of circular arch rubber

支撑面越大所能承受的荷载也越大。l是影响拱状橡胶支撑面大小的尺寸参数，l越小支撑面越大，因此，当l值改变时竖向刚度变化明显。不同的5组整体因素作用下，竖向刚度的变化曲线近乎平行，说明这3个尺寸参数的整合符合竖向刚度的整体变化规律，在l=29时，5个水平整体因素的竖向刚度都出现向下偏移，这说明了支撑面太小会引起装置的不稳定并且竖向刚度会出现明显的下降趋势。

根据各个模拟工况的对比情况，竖向刚度与单因素l和h1，h2，r整体因素有关，从影响规律和尺寸意义上进行分析，将h1，h2，r3个尺寸参数进行整合，得到竖向镂空系数T。利用MATLAB进行拟合分析，将l和T值作为自变量，竖向刚度作为因变量，对以上模拟数据进行两参数影响的最小二乘法线性拟合，得到竖向刚度的拟合计算公式Ku。

(7)

Ku=425-16.45l+144.1T

(8)

模拟值和拟合值对比如图12所示，从图12可看出，共利用55组模拟数据进行拟合，拟合值和模拟值很接近，最大误差为16%，最小误差为1%，说明拟合效果较好。为了分析拟合公式的适用性，将未作为拟合样本数据的正交设计工况代入拟合公式进行复核，结果如表8所示。在正交设计工况模拟结果中，拟合值与模拟值也较为相近，最大误差为16.9%，最小误差为0.4%，与样本数据反应的误差也较为一致，这说明了该支座竖向刚度的拟合公式具有一定的适用性。

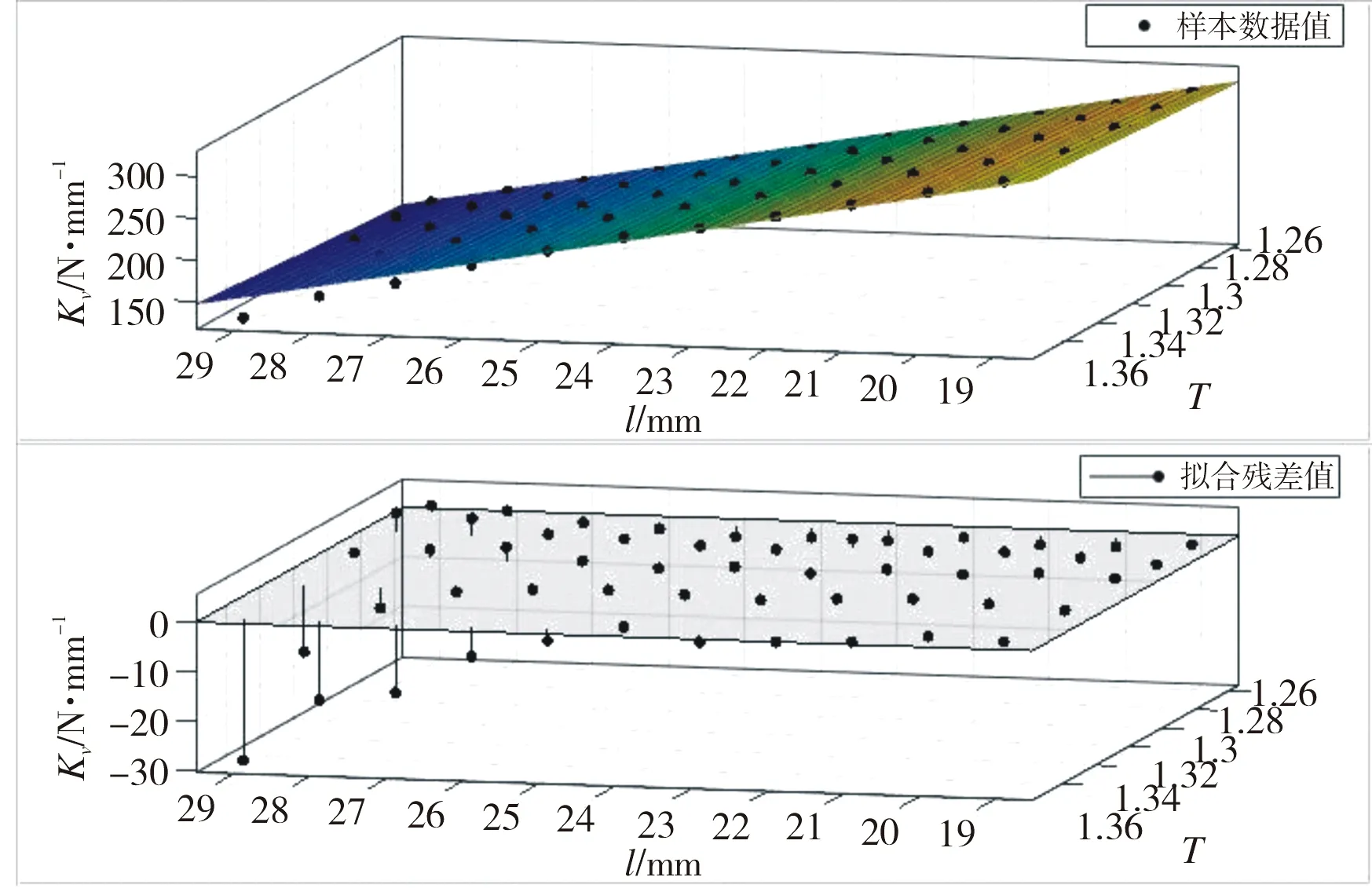
图12 竖向刚度模拟值和拟合值对比图Fig.12 Comparison of simulated and fitted values of vevtical stiffness

表8 竖向刚度模拟值与拟合值Table 8 Simulated and fitted values of vertical stiffness

4 结论

本文在原有的橡胶支座的基础上，针对文物储藏柜的特点，设计了一种中部拱状镂空的拱状橡胶三向隔震支座，并探究了影响该支座竖向刚度的因素及影响规律。

(1)拱状橡胶三向隔震支座具有良好的承载力，试验尺寸的单个支座保证正常使用的承载力极限为1 384.89 N，并且竖向刚度较为稳定，随上部荷载的变化较小。由于加工工艺和圆拱橡胶形状特性的影响，支座有最小载荷要求，本文尺寸支座的荷载要求为 ≥250 N才能充分发挥支座的竖向性能。

(2)拱状橡胶三向隔震支座的4个尺寸参数对支座竖向刚度的敏感度为l>h1>h2>r，其中r与竖向刚度成正比，其余为反比。结合各个尺寸参数的敏感度大小进行了因素整合，将影响较大的l作为单因素考虑，将影响较小的h1，h2，r作为整体因素考虑。

(3)在不改变材料属性和整体尺寸的情况下，通过受力分析和影响规律确定l和竖向镂空系数T为主要影响因素，利用MATLAB进行拟合得到竖向刚度的拟合计算公式，并且进行了样本数据外的结果复核，最大误差不超过16.9%，并且大部分数据误差都在10% 以内，说明该公式具有一定的适用性。