基于ABAQUS水闸与地基相互作用机理分析

徐 瑞，唐子明

(江苏省淮沭新河管理处，江苏 淮安 223001)

近年来，随着“一带一路”、西部大开发、西电东送等战略的开展，大量基础设施如水电站、川藏铁路等正处于紧密的建设当中[1]。但一些水电站闸址区常修建于黏土地基之上，在水电站蓄水之后，过大或不均匀地基沉降将导致水闸与底板之间产生拉应力，严重威胁水闸的安全运行，引发地质灾害发生，造成人员和大量经济损失[2]。因此，分析蓄水后地基沉降及水闸与地基之间的相互作用是水闸安全运行的关键问题[3]。

目前，国内外通常采用数值模拟的方法来分析地基沉降或者与建筑结构之间的相互作用，其常用的数值理论包括有限元法[4]、有限差分法[5]、离散元法[6]等。其中，由达索公司基于有限元方法开发的ABAQUS软件有着成熟的理论基础，当中包含多种类型的材料模型库，可以模拟土壤与岩石等地质材料的应力应变以及位移变形分析，同时还能对结构的静力与动力响应进行模拟，因此被广泛用于水工结构稳定性分析[7]。李伟康等[8]利用ABAQUS结合工程实例,通过有限元法分析了在软弱土层上桩的局部合理布置密度，并计算和比较不同条件下地基局部加固效果后的底板拉应力变化情况。梁景奇[9]以某开敞式水闸为研究对象，釆用平面简化法对水闸闸室进行了稳定计算，并利用ABAQUS有限元软件建立闸室三维有限元模型，对水闸闸室进行稳定计算以及结构分析。李路华[10]利用ABAQUS有限元软件,结合具体的工程实例,进行三维建模计算,模拟分析了某护镜门型式水闸底板采用闸墩分缝和底板分缝时,对于不同的荷载工况,其相应的受力及变形情况，为工程实际提供设计依据。丁立魁[11]利用ABAQUS有限元软件，对吹填区内一水闸工程进行了基于共同作用理论的上部水闸结构-基础-软基的整体数值分析。

本文以四川某水电站闸址为例，采用ABAQUS建立三维水闸与地基模型，采用M-C模型分析水闸与地基的相互作用，同时分析水闸与地基应力分布、水闸横河与顺河向应力数值变化规律以及水闸横河与顺河向与地基的位移。研究结果可为相关工程分析提供参考。

1 模型建立与计算参数

本次建立的水闸地基模型位于四川某水电站，为平底开敞式水闸，最大过闸流量为19 300 m3/s,，闸孔净宽 为14.8 m, 中墩宽为2.5 m, 缝墩宽为3.6 m, 边墩宽为2 m, 水闸混凝土底板厚1.3 m。闸室内设有工作门槽一道, 检修门槽两道; 闸室顺水流向的长度为28 m。此外，整个地基深度取80 m。经现场勘查，地基材料可分为6层，从上往下依次为灰黏土、黏土1、黏土2、粉质黏土、细砂子以及紧砂。根据室内试验测试黏土矿物主要包括有蒙脱石、伊利石等，碎屑矿物主要有石英与长石，其次含有少量方解石。通过对部分黏土样进行物理力学性质测定，测得其密度为1.8 g/m3，干密度1.36 g/m3，含水率15%，塑限含水率20%，液限含水率38%，塑性与液性指数分别为24和0.26。此次的黏土计算参数分别取自试验结果的平均值，而细沙与紧砂的取值参考工程地质手册取经验值。另外，本文考虑的计算工况为上游满蓄水的极端条件工况，本构采用M-C屈服理论。图1为本次概化模型尺寸，表1为本次计算力学参数。

图1 水闸与地基概化三维模型

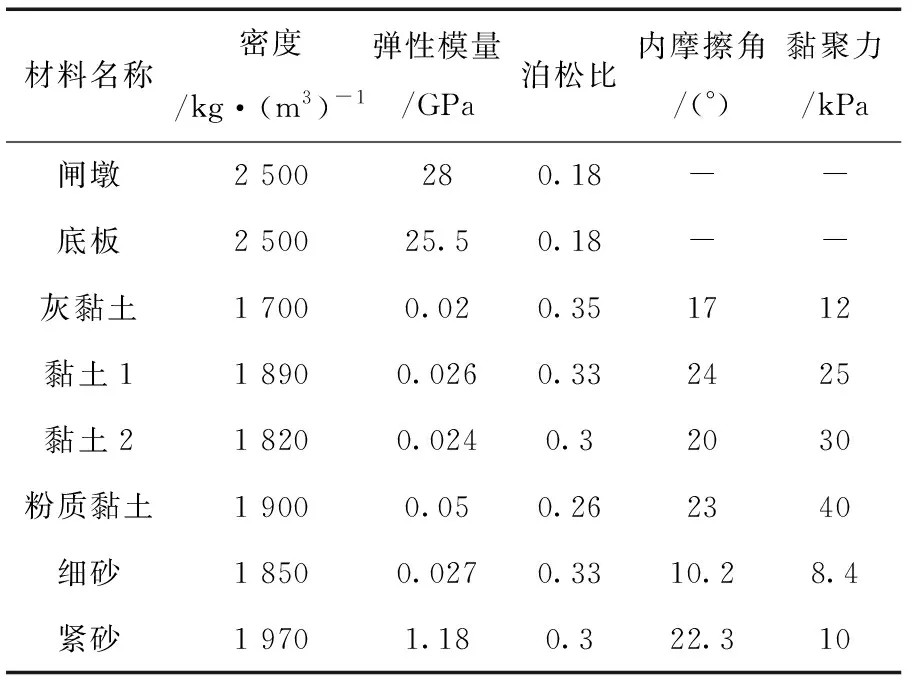
表1 模型计算力学参数

2 M-C理论

M-C理论又称库仑强度理论, 材料的破坏是剪切破坏，当任意平面上的剪应力等于材料的抗剪强度时该点就发生破坏。破坏面上的剪应力(剪切强度)取决于剪切面上的正应力和土的性质。而在工程上，通常采用摩尔库伦屈服模型来描述土的变形。M-C模型主要适用于在单调荷载下的颗粒状材料，其屈服面函数可由下式表达：

F=Rmeq-ptanφ-c=0

(1)

其中：φ为q-p平面上M-C屈服面的倾角，其物理意义代表土体摩擦角；c为材料的黏聚力；参数Rme可由下式表示：

(2)

式中：Θ为极偏角。

由于M-C模型屈服面存在尖角，相关联流动法无法正确描述塑性流动方向，给数值计算带来极大的不便，因此ABAQUS中采用连续光滑的椭圆函数作为塑性势面：

(3)

式中：ψ为剪胀角；c|0为初始黏聚力；ε为子午面上的偏心率，控制G在子午面形状与函数渐近线之间的渐近线；Rmw计算由下式给出：

(4)

式中：e为π平面上的偏心率，范围在0.5～1。

3 数值结果分析

3.1 水闸与地基应力分布分析

图2为此次计算的模型应力云图。由图2可知，在蓄水条件下，水闸与闸底板受影响最大，闸墩与底板交界处有应力集中现象，其中中墩底端的应力最为集中。此外，从图2中还可看出，蓄水后，拉应力区几乎集中在闸室附近，闸墩的拉应力范围大致在闸墩的1/2～1/3处。综合图3模型的竖直方向应力云图来看，地基土主要受压应力影响明显，底板与水闸之间的相互作用明显大于水闸与地基之间的相互影响。从图4的模型总位移云图可知，水压力对水闸所产生的推力，使得闸体应力与位移发生变化，同时导致水闸-底板-地基三者之间相互影响。其中，闸墩的拉应力导致底板应力改变，进而导致地基土应力的重分布，但由于地基为分层复合地基，各土层刚度不一致，产生应力集中或应力扩散效应，从而产生不均匀沉降，再次影响水闸的应力与沉降。此次计算，地基受影响的范围为41.2 m。因此，在复合地基上建造水闸时，必须充分考虑水闸-底板-地基三者之间的影响关系，最大程度减少地基不均匀沉降所导致的闸墩底部拉应力数值与范围。

图2 模型米塞斯应力云图

图3 模型竖向米塞斯应力云图

图4 模型总位移云图

3.2 水闸横河与顺河向应力数值变化规律

为进一步分析水闸的应力变化规律，将通过边墩和中墩底端的横河方向节点应力输出，见图5。由图5中的变化规律可知，中墩低端的拉应力最大，约2.8 MPa，这与图2中的应力分布规律一致。而随着左右两端距离增大，应力逐渐减小到一定值后，又逐渐增加，整体上呈W形。此外，左右边墩的拉应力具有较大差值，其中左边墩为0.6 MPa，右边墩为2.4 MPa。为分析下游水闸横河墩底应力变化规律，将下游水闸过墩底节点应力输出，见图6。

图5 横河监测点应力

图6 下游横河监测点应力

图6中，拉应力最大值同样产生于中墩底端附近，而边墩的应力数值变化较缓，整体呈倒V形。

图7为右边界顺河方向水闸节点应力。由图7可知，此边界上的应力随距离增加呈W形，但内在规律与横河的变化规律截然不同。图7中最大拉应力发生在右墩底端，约2.4 MPa，而后当相对距离为17.1 m时达到拉应力最小值，为0.37 MPa。

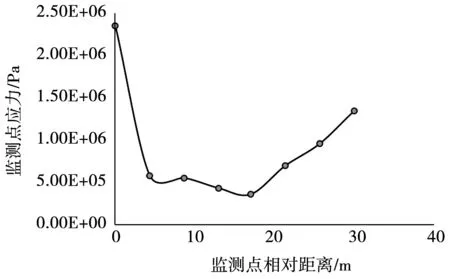
图7 下游顺河监测点应力

3.3 水闸横河及顺河向与地基的位移分析

图8为水闸上游横河向的总位移(水平面两个直角方向)变化规律，其中监测节点与3.2中的节点一致。由图8可知，由于水闸应力不均匀，其横河向的位移变化同样有差异。其中左边墩的位移最大，达到约6.5 mm的沉降，而中墩由于受拉应力的影响，总位移最小，约为6.2 mm，整体变化呈V形。此外，结合图5中的横河监测点应力变化规律可知，水闸的上游位移值与结构所受拉应力的值大致呈负相关。图9为水闸下游横河向的总位移变化规律。

图8 水闸上游横河向的总位移变化规律

图9 水闸下游横河向的总位移变化规律

由图9可知，水闸下游的位移大致与上游相差一个数量级，这是由于下游的拉应力要小于上游的拉应力，因此总的位移变化要小于上游水闸的变化量。但值得一提的是，下游总位移的最大值对应于拉应力最大值，这与上游的变化规律相反。

图10为水闸顺河向的总位移变化规律。由图10中可明显看到，水闸蓄水一侧的位移变化量要明显大于无蓄水侧的位移变化量，且随着顺河向相对距离的增加，水闸的位移变化量呈线性关系减少。其中最大位移值约为0.63 mm，最小为0.3 mm。图11为水闸下竖向地基的位移变化量。由图11可知，同一个路径上，地基的位移变化具有明显的差异，其总位移的变化不仅在数值上具有明显波动，在方向上同样具有不同的变化趋势。在18 m的深度左右，总位移为正值，18 m以前为负值，同时总位移随地基深度增加呈多峰变化。

图10 水闸顺河向的总位移变化规律

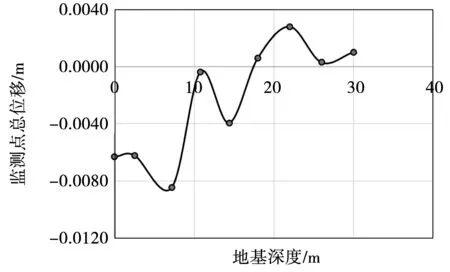
图11 水闸下地基的位移变化量

4 结 论

本文采用ABAQUS建立了三维水闸与地基模型，采用M-C模型分析了水闸与地基的相互作用，同时分析了水闸与地基应力分布、水闸横河与顺河向应力数值变化规律以及水闸横河及顺河向与地基的位移。主要结论如下：

1) 在蓄水条件下，水闸与闸底板受影响最大，闸墩与底板交界处有应力集中现象，其中中墩底端的应力最为集中。此外，拉应力区几乎集中在闸室附近，闸墩的拉应力范围大致在闸墩的1/2～1/3处。

2) 水闸上游横河向，中墩底端的拉应力随着左右两端距离增大，整体上W形，而下游横河向整体呈倒V形。此外，右边界顺河方向水闸节点应力。随距离增加呈W形，但内在规律与横河的变化规律截然不同。

3) 地基的位移变化具有明显的差异，其总位移的变化不仅在数值上具有明显波动，在方向上同样具有不同的变化趋势。在18 m的深度左右，总位移为正值，18 m以前为负值，同时总位移随地基深度增加呈多峰变化。