压入式通风掘进巷道粉尘悬浮运移规律研究

陈绍杰，祁银鸽，李改革

（华北科技学院 安全工程学院，河北 三河 065201）

煤炭是我国的主体能源，在国家经济、社会等各方面都发挥着重要作用。随着煤矿采掘机械化程度的不断提高，井下粉尘的污染问题日益突出[1]。近年来，随着计算机应用技术的快速发展，越来越多的学者将数值模拟技术应用于矿井粉尘运移规律及防治工作的研究。姚玉静等[2]通过建立符合现场实际的掘进巷道模型并进行模拟，得出了长压短抽式通风掘进巷道中粉尘质量浓度的分布规律；王冕[3]利用数值模拟软件和掘进巷道相似模拟实验，研究了压入式通风掘进巷道流场对粉尘运移和沉降的影响规律；姜婉[4]运用相似实验和数值模拟相结合的方法，分析了不同风筒高度和风筒与工作面距离及不同风量时的巷道流场及粉尘分布特征；王凯等[5]利用理论分析和数值模拟方法，研究了在供风量一定时，不同直径风筒对巷道内的粉尘运移规律的影响；胡胜勇等[6]基于气固两相流理论，通过编程计算了综掘工作面气载粉尘运移过程，研究了高瓦斯煤层综掘工作面气固两相流动特性。

综上所述，目前对于掘进巷道内粉尘运移规律的数值模拟研究，主要集中于掘进工作面和巷道内粉尘质量分数分布及运移规律上，而对于不同风速下掘进工作面粉尘在巷道内空间分布及悬浮、沉降的时间规律研究较少。然而，掌握不同风速下巷道内粉尘空间分布和悬浮时间规律是做好通风系统设计及井下粉尘防治工作的关键。因此，在掘进巷道压入式通风系统的基础上，模拟分析风筒出风口不同风速及风筒距掘进工作面不同距离的情况下，粉尘在掘进巷道内的空间分布和悬浮、沉降规律，以期为治理井下掘进巷道粉尘污染提供理论支持。

1 掘进巷道粉尘运移数学理论及模型

1.1 气固两相流理论

掘进巷道内部的粉尘在空气中的分布属气固两相流范畴，因此选用气固两相流数学模型对粉尘运移轨迹及悬浮规律进行研究。气固两相流动的研究方法有2 种：①欧拉-欧拉法，亦称为多相流方法；②欧拉-拉格朗日法，或称颗粒轨道法[7]。研究采用欧拉-拉格朗日模型的离散相模型（DPM）对粉尘在风流场中的轨迹进行模拟，即空气为连续相，粉尘颗粒为离散相，用欧拉观点对气相流场进行描述，而用拉格朗日观点描述颗粒运动。考虑离散相与连续相之间的耦合作用[8]。

1.2 控制方程

1.2.1 连续相控制方程

掘进巷道空气流动满足由3 大基本物理定律推导出的连续性方程、动量方程（Navier－Stokes 方程）、能量方程组成的方程组[9]，将巷道内风流视为不可压缩流体，有作为求解控制方程组的微分形式表示。

连续性方程：

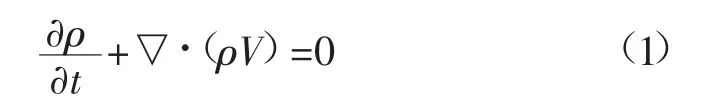
式中：ρ 为流体密度，kg/m3；t 为时间，s；▽为拉普拉斯算子；V 为流体速度矢量，m/s。

动量方程：

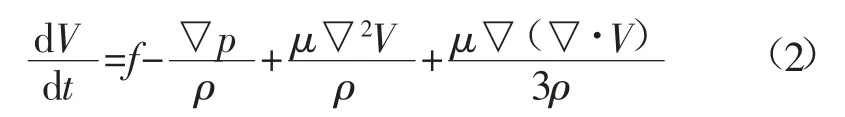
式中：f 为单位质量流体的体积力，N；▽p 为流体压力梯度，Pa/m；μ 为动力黏度系数。

能量方程：

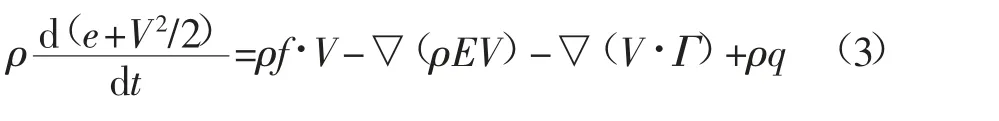
式中：e 为单位质量流体的内能，J；E 为总动能，J；Γ 为表面应力，N；q 为单位质量的体积加热率，（W·m3）/kg。

湍流模型选用标准的k-epsilon 模型，即湍流长度和时间尺度分别通过求解2 个单独的运输方程来计算[10]。

湍动能k 的运输方程为：

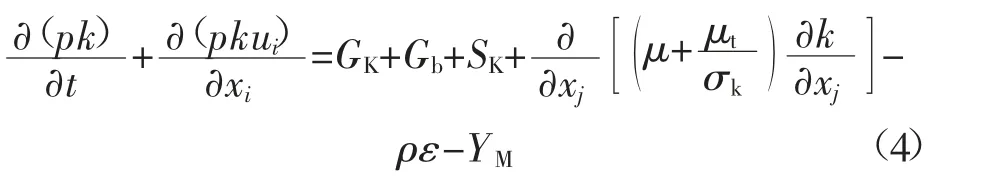
式中：k 为湍动能，m2/s2；ui为i 方向上平均速度分量，m/s；xi、xj分别为i、j 方向上的水平距离，m；GK为由平均速度梯度产生的湍动能，kg/（m·s3）；Gb为由浮力产生的湍动能，kg/（m·s3）；SK为方程的源项，kg/（m·s3）；μt为湍流黏度系数；σk为流体的k 的无量纲湍流普朗特数；ε 为湍流耗散率，%；YM为可压缩流动中波的膨胀对整体扩散率的影响，kg/（m·s3）。

湍动耗散率ε 的运输方程为：

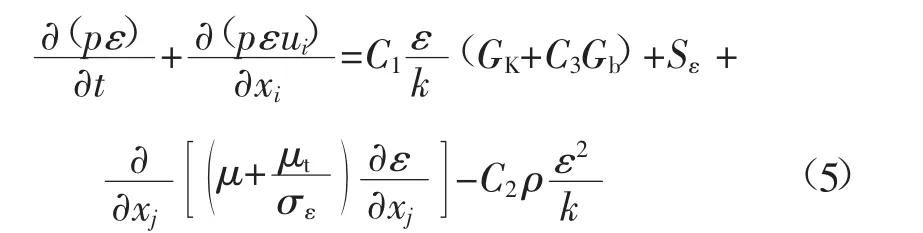
式中：C1、C2、C3为常数；Sε为源项，m2/s4；σε为ε的无量纲湍流普朗特数。

式中：Cμ为常数。

1.2.2 离散相控制方程

在FLUENT 求解连续相的输运方程收敛的基础上，采用DPM 方法描述和追踪掘进巷道中的粉尘颗粒，并通过对离散相作用力微分方程求解，来获得颗粒在拉格朗日坐标系中的轨道[11]。其方程为：

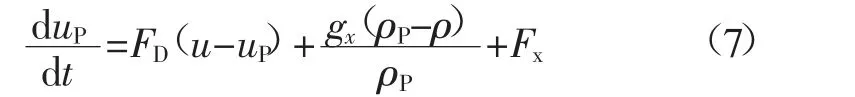
式中：uP为离散相速度，m/s；FD（u－uP）为离散相的单位质量曳力，N；u 为流体相速度，m/s；gx为x 方向的重力加速度，m/s2；ρP为离散相密度，kg/m3；Fx为其他作用力，N。

式中：CD为曳力系数；dP为颗粒直径，m；Re 为相对雷诺数（颗粒雷诺数）。

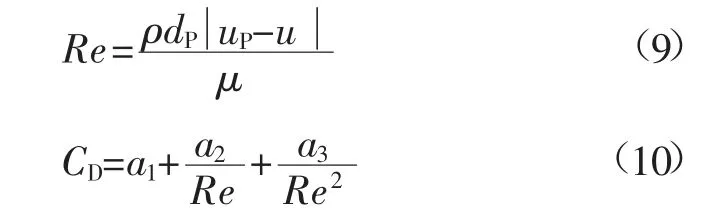
式中：a1、a2、a3为常数。

2 掘进巷道几何模型及参数设定

2.1 几何模型

根据现场实际及计算机运算能力，对掘进巷道进行适当简化：选取掘进工作面及其后30 m 作为研究对象，使用建模软件Gambit 建立长30 m、宽5 m、高3 m 的长方体掘进巷道模型。掘进巷道几何模型如图1。其中，掘进机采用EBH-120 淮南煤机，并将其简化为长2.1 m、宽0.82 m、高0.95 m 的距掘进工作面1 m 的长方体；压入式风筒直径0.8 m，悬挂于巷道左侧，风筒出风口与工作面距离为5 m，风筒的轴线距巷道顶板和巷帮均为0.5 m。

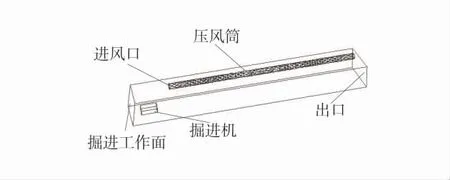
图1 掘进巷道几何模型Fig.1 Driving roadway geometry model

2.2 网格划分

在几何模型中，网格划分的方法和网格的数量及质量对数值模拟求解精度有着重要影响。由于Fluent 只能读取非结构网格，因此使用Gambit 中自带的网格划分系统对几何模型进行非结构网格划分。选取Tet/Hybrid 类型，使用TGrid 方法，将模型主体划分为四面体网格单元。Interval size 取0.4，为使计算更为精确，在风筒出风口、风筒曲面及风流与掘进机交汇面等流场复杂、阻力较大处使用包含六面体、锥形和楔形的混合网格。网格划分三视图如图2，共包含44 698 个单元格，9 570 个结点。

图2 网格划分三视图Fig.2 Grid mesh divided into three views

2.3 参数设置

巷道掘进时，主要产尘点为掘进工作面，因此将整个掘进工作面设为尘源。粉尘颗粒粒度分布选用罗辛-拉姆勒（R-R）分布。模拟采用标准k-ε 方程和SIMPLEC 算法，计算压入式通风方式下，在掘进巷道内的风流场，单相风流场收敛后，创建离散相粉尘颗粒，使用DPM 模型与连续相进行耦合计算并求解。边界条件参数设定见表1，粉尘源参数设定见表2。

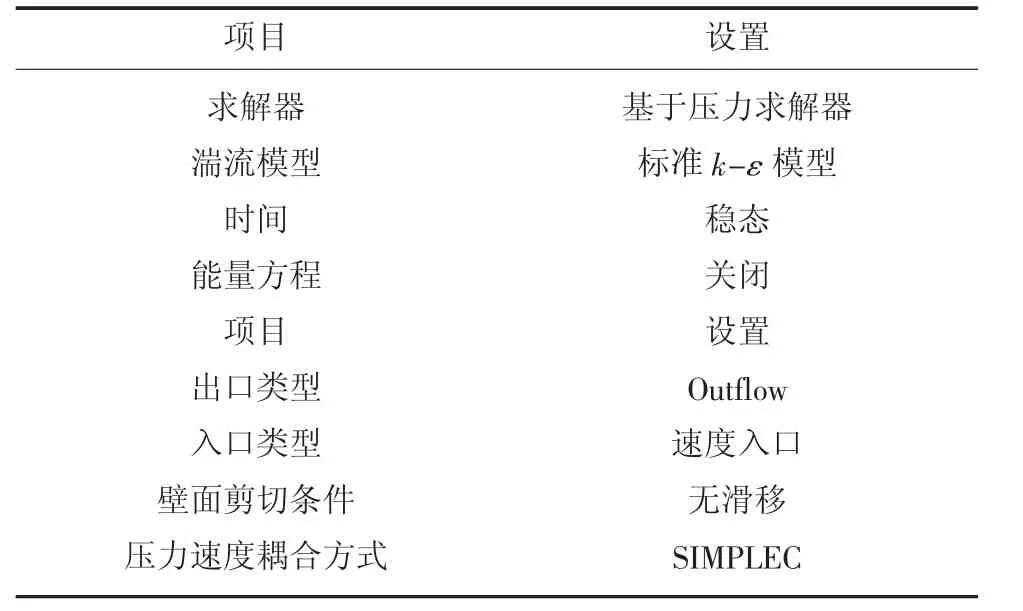
表1 边界条件参数设定Table 1 Boundary condition parameters setting

表2 粉尘源参数设定Table 2 Dust source parameters setting

3 数值模拟结果

3.1 风流场分布

掘进巷道中粉尘的扩散运移受到多种因素共同影响，其中影响最大的是空气的流场分布，因此掌握风流场的分布规律有助于分析粉尘的扩散运移规律。基于此，主要研究井下职工呼吸带处粉尘悬浮规律，0.5～1.5 m 左右的高度通常被认为是呼吸带的高度；而煤矿井下，行进中的矿工呼吸带的位置可以看作是顶板垂直向下0.4 m 左右处。由于掘进机和带式输送机的存在，掘进工作进行时，司机距工作面2 m 左右，巷道中人行道位于压风筒的对侧。压入式通风掘进巷道，不同出风口风速下x=2 m、y=-2 m、z=1.5 m 截面速度分布云图如图3～图5。

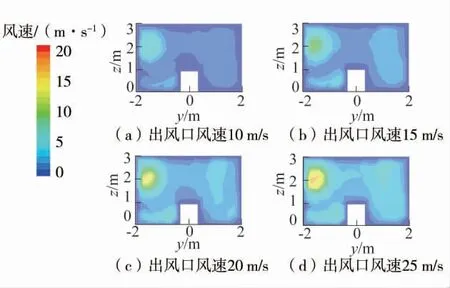
图3 不同出风口风速下x=2 m 截面速度分布云图Fig.3 Diagrams of cross-section velocity distribution at x=2 m under different air outlet wind speed

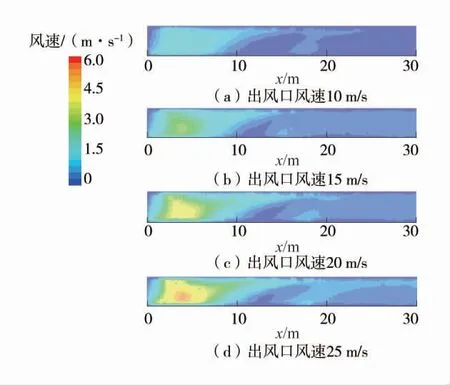
图4 不同出风口风速下y=-2 m 截面速度分布云图Fig.4 Diagrams of cross-section velocity distribution at y=-2 m under different outlet wind speed

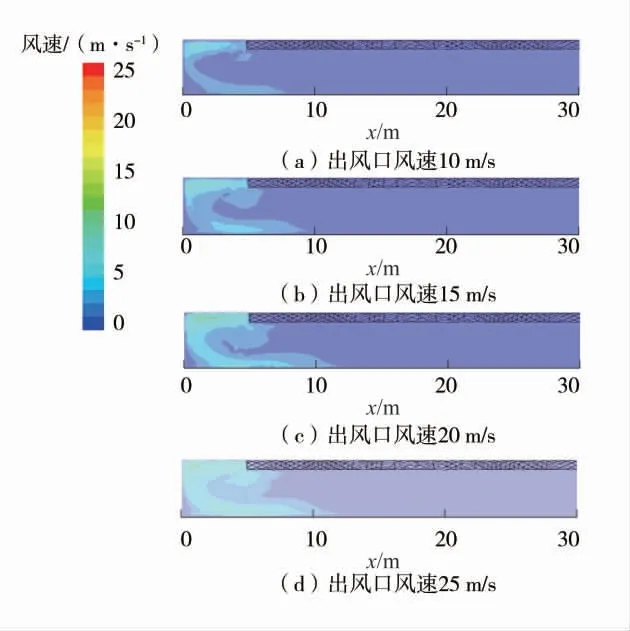
图5 不同出风口风速下z=1.5 m 截面速度分布云图Fig.5 Diagrams of cross-section velocity distribution at z=1.5 m under different air outlet wind speed

由图3 可知，掘进巷道沿y 轴的速度分布呈现出“大-小-大”的趋势，压风筒下侧及对侧风速较大，而由于掘进机和钻机等设备的影响，巷道中部风速较小。随着风速的增加，巷道两侧和中部的风流风速差距更为明显，但风流速度的集中区域有所变化，主要集中于压风筒下侧及其对角处。

由图4 可知，空气速度在x=8 m 处开始减小，又在x=15 m 处有1 个短暂的增大，最后从x=17 m处开始趋于稳定。但随着风速的增加，空气速度2 次增大点提前至x=12 m 处，并在x=3 m 处逐渐形成涡流区域。这是由于随着风筒出风口风速的增加，巷道内部的空气速度受掘进设备及巷道有限空间的影响加大，最终形成了明显的涡流结构。

由图5 可知，在z=1.5 m 行人呼吸带高度处，空气速度由掘进工作面开始沿x 轴方向减小，并从x=10 m 处开始稳定在2.5 m/s；随着风筒出风口风速的增大，靠近掘进工作面的高速区域随之扩大，并逐渐在x=3 m 处形成涡流区域。

3.2 风速对粉尘颗粒悬浮时间的影响

煤矿井下在进行掘进作业时，巷道内风流速度是影响综掘工作面所产粉尘悬浮及运移的主要因素，因此模拟了4 种不同风筒出风口风速下粉尘悬浮情况。压入式通风巷道，不同出风口风速下粉尘运移轨迹如图6。

图6 不同出风口风速下粉尘运移轨迹Fig.6 Dust movement track under different air outlet wind speed

由图6 可知，由于掘进设备和巷道有限空间的影响，空气风流会在x=3 m 即掘进机处形成涡流区域，因此大量粉尘会在此处随风流做涡流悬浮；随着风速的增大，涡流越来越明显，悬浮的粉尘量也随之增大，但悬浮时间明显缩短，这是因为风速增大，粉尘颗粒所受的离心力也随之增大，在强大离心力的作用下，大量粉尘悬浮2～4 s 便被巷帮及巷道顶底板所捕捉，无法随风流排出巷道。另一方面，风速的增大也对巷道的通风除尘造成了较大影响，风速的增加能够缩短粉尘悬浮和排出巷道的时间，同时也大大增加了除尘效率，图6（d）较图6（a）的出口粉尘排出速度及排尘量增大。

3.3 风筒位置对粉尘颗粒悬浮时间的影响

《煤矿安全规程》明文规定：掘进巷道必须采用矿井全风压通风或者局部通风机通风。因此，局部通风的风筒位置的变化也是影响掘进巷道内的粉尘悬浮规律的重要因素。在研究风筒位置对粉尘悬浮规律的影响时，设定风筒出风口风速25 m/s 不变，在原有距离为的5 m 模拟结果基础上，增加风筒距掘进工作面6 m 和8 m 的2 组模拟实验。不同距离下粉尘运移轨迹如图7。

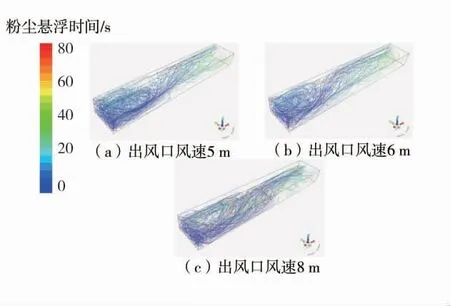
图7 不同距离下粉尘运移轨迹FIg.7 Dust movement track at different distances from the driving working surface

由图7 可知，随着压入风筒距掘进工作面越来越远，原有掘进机处的涡流逐渐紊乱，粉尘在巷道中部的扩散越发严重，悬浮时间加长。压入风筒与掘进工作面距离越远，风流到达掘进面的风速越小，工作人员作业区域粉尘扩散越严重，排尘效果越差。从巷道尾部及出口可看出，粉尘轨迹紊乱程度逐渐增加，悬浮时间增大，出口排尘量减小。

4 结 语

1）基于Gambit 软件，建立了符合井下实际掘进巷道的几何模型，为进一步研究掘进巷道不同风速和不同风筒位置下粉尘运移规律模拟提供保障。

2）根据气固两相流理论，采用标准的k-epsilon模型和离散相模型（DPM）分别对压入式通风掘进巷道风流场和粉尘悬浮规律进行数值模拟，得出风流在掘进设备处形成涡流区域，并沿y 方向呈现出“大-小-大”的趋势，最终在巷道中部开始趋于稳定。

3）分析得出不同风筒出风口风速下压入式通风掘进巷道中粉尘悬浮规律，即随着风速的增大，粉尘悬浮量也随之增大，但由于高速离心力的作用，悬浮时间减短，粉尘迅速被巷帮及顶底板捕捉；风速的增大同时增大了通风除尘的除尘效率。

4）压入风筒与掘进工作面距离越远，粉尘在巷道中扩散越严重，悬浮时间越长；同时粉尘轨迹紊乱程度增加，巷道出口处通风除尘的排尘量减小。