拘束模回转试验的CFD最优设置提取与多子样验证

梁 川，赵 峰，李胜忠

（中国船舶科学研究中心，江苏 无锡 214082）

0 引 言

CFD应用技术的突破是近二十余年来船舶水动力学界最具影响力的技术进步之一。随着计算机性能的快速提升和相关CFD算法的深入发展，CFD被广泛应用于模拟各种真实外形的复杂流动，成为解决许多实际工程问题的利刃，逐渐形成了数值水池虚拟试验的应用研究手段[1-2]。同样伴随而来的是CFD模拟结果的置信度越来越被关注。

关于CFD模拟的置信度研究，目前已经历了30余年的发展，AIAA和ITTC等相关组织都相继提出了各自的置信度分析推荐规程[3-4]，推荐规程的主体形式是基于网格收敛分析和Richardson 外推法的不确定度分析。自ITTC 的CFD 不确定度分析规程发布之后，国内外船舶水动力学界的诸多研究人员基于此开展了大量应用研究和实践工作[5-8]。通过实践，可以发现该方法具有学术性强、理论清晰、数学推导严谨等优点，因而在船舶水动力学界具有较大影响力。

与此同时，通过应用实践也发现该方法的一些不足之处，例如：难以分析和评估多种因素之间的交互影响；实际应用中一般主要针对网格开展不确定度分析，且主要适用结构化网格；对于很多实际工程问题，难以得到一致收敛的结果从而导致不确定度无法评估。总体上看，目前ITTC 的CFD 不确定度分析推荐规程，学术性大于工程实用性，限制了其在工程应用上的大范围推广。

CFD 技术通常的应用路径为：针对某一类问题，首先对标某一典型试验结果，寻找一组最优的参数搭配，然后应用该组搭配去预报新的工况，最后在给出预报结果的置信度时去参照典型算例结果。该路径中对于CFD 预报结果的最大质疑为：对标某一有试验结果的工况获得的最佳参数搭配不一定适用于新的工况，通过典型算例的误差去判断新工况的误差难以令人信服。

如何最大限度的破解这一质疑，是影响CFD 技术应用推广的关键。目前，一种以“大子样验证”为特征的多重验证方法[9～13]提供了一种新的思路，其核心是“不确定度分析、最优解确认、大子样验证”三重验证流程，并针对最常规的一类问题——船模阻力试验，进行了40 条船模、332 个样本点的大子样验证分析（相关结果见图1）。该方法在传统不确定度分析方法的基础上（通过对少量典型算例进行较为严密细致的研究以确立CFD 求解器较为可靠的品“质”），进一步引入“量”的覆盖性，通过对大量数值模拟结果和相应试验结果的对比与统计分析，从而给出更加可信的CFD模拟置信度的概率分布。

图1 基于大子样验证的船模阻力模拟误差概率分布Fig.1 Probability distribution of errors on simulations of big-sample ship model resistance

目前基于多子样统计分析的思路对CFD 模拟置信度进行评估，在行业仍属于提出和待检验阶段，还需要进行不断的改进和完善。例如，目前方法只是针对船模阻力这类流动相对简单的问题进行了多达332 个样本点的验证分析，对于流动复杂、子样较少的问题，新方法的适用性仍存疑。归纳起来有这两点：（1）目前只是针对船模静水阻力性能这类流动分离较小的问题进行了大子样验证，能否适应更加复杂的流动问题值得深入研究；（2）对于复杂流动问题，物理试验数据子样往往不多，能否在相对较少的子样情况下进行统计验证同样值得研究。

本文针对操纵性拘束模试验中开展的相对较少的旋臂回转试验，以8 条CSSRC 系列集装箱船的物理试验数据为基础展开相关验证研究。

1 CFD数值模拟大（多）子样验证方法

目前，取得一定共识的CFD 模拟置信度评估方法大部分是基于Richardson 外推法。其核心思想是试图区分模型误差与数值误差。理论上，当时间和空间的离散尺度趋近于零时，数值误差将趋近于零，这时便可以获得理论模型的解，从而区分模型误差与数值误差，进而为模型改进提供指导。实际上，CFD求解的是一组强非线性的控制方程，计算模型、数值格式、离散网格（形式、数量、质量）及数值计算方法是相互影响、强耦合的，定量细化网格尺度时还容易遇到计算发散或者计算结果无法一致收敛等情况。这些都在一定程度上限制了该不确定度分析方法的大范围应用。

总的来看，传统的不确定度分析方法是基于分析的思路，针对少量典型算例进行严密细致的研究，能够基本确立所用CFD求解器较为可靠的品质。本文从归纳的角度将各类误差综合考虑，即着眼于工程实用，紧紧围绕如何使得CFD模拟结果与试验结果相比误差最小这个目标，通过调整影响CFD模拟结果的诸多参数来逼近试验结果。需要说明的是，参数调整主要针对“最优设置提取”这一步骤，一旦设置确定，在采用大子样验证时需保证其一致性。

具体到CFD 实践中，首先需要做的是对应用问题进行分类以提高CFD 工具针对特定问题模拟的准确性；然后，通过对标某一（或少量）典型试验结果，寻找到一组最优的参数搭配来逼近试验结果，进而建立起（该组参数搭配下的）CFD 模拟与物理实际之间的联系和信任；最后试图将这一联系和信任推广到更加广阔的应用域中。其中，最为关键的是推广这一步。直接利用典型算例的误差去评估新算例的误差容易引起质疑，即对标获得的最佳参数搭配不一定适用于新的工况；引起质疑的深层次原因是新工况与对标工况之间的差异很难量化表达；如何破解这一难题，需要从工况特征的细化入手，也就是需要加入更多的工况样本点，这群工况样本点将构成一个离散的样本空间；采用所获得的最佳参数搭配对样本点工况进行CFD 模拟，根据统计结果可以给出该样本空间的CFD 模拟置信度概率分布；假如新的工况落在该样本空间范围内，则可以对新工况的置信度给出合理的置信度评估。目前，关于样本点的数目要求，还未有一个具体的说法。一般样本数目大于100，可以称作大子样验证；样本数目介于10和100之间，可以称作多子样验证。

2 分离流动模拟最优参数搭配提取

阻力性能主要考察船舶沿中纵剖面直线航行的性能，其流动分离较小；操纵性主要研究船舶改变航向航态的能力，操纵运动时船体的速度与中纵剖面存在一定的偏角，这将导致流动分离等复杂流动现象，如何较好地模拟这类分离流动是操纵性计算的重点和难点。经过分析目标应用问题的流动特点，可以提炼出主要的科学问题以便更好地模拟大分离流流动。

需要说明的是，关于“最优参数搭配”，其与所用的CFD 求解器高度相关，最优参数搭配的具体数值需要根据具体求解器的特点去获取。关于“最优”的理解，不是理论上的最优，而是实践中所能获得的最优。本文基于自主CFD 求解器（主要特征为采用基于结构化重叠网格方法的RANS 求解器），首先从船模阻力模拟最优参数搭配入手，以标模KVLCC2的偏航运动[14]这类典型的大分离流动现象为例展开研究，获得了适合于所用CFD求解器的操纵性拘束模虚拟试验的最优参数搭配，下面将对其进行概要描述。

船模阻力计算是操纵性计算的基础，表1 为经过长期实践所获得的船模阻力模拟的最优参数设置，可为拘束模操纵性计算最佳参数搭配的获取提供一个较好的初始输入。

首先，采用表1中的阻力计算最优设置，对KVLCC2偏航运动进行计算发现，侧向力和摇艏力矩偏差较大（参见表2中L150Y45列数据，侧向力平均误差为-18.2%，摇艏力矩误差为15.9%），需要进一步优化参数设置。

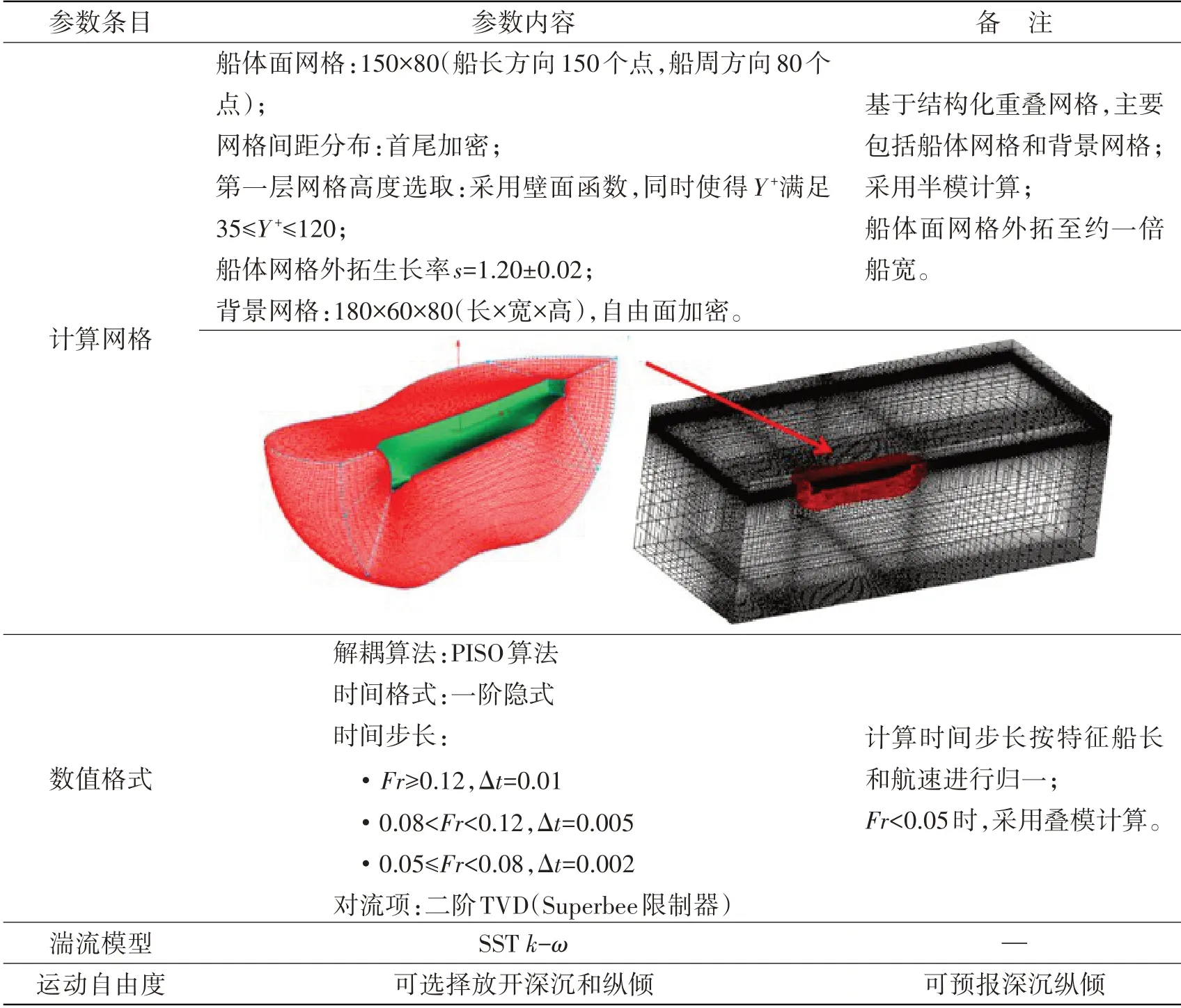
表1 船模阻力模拟最优参数设置Tab.1 CFD best practice for resistance simulation

在影响CFD计算结果的参数中，根据参数变更的便捷程度，大体可以分为两类：一类为网格参数；一类为非网格参数。网格参数需要重新生成计算网格，而非网格参数的更改方便、容易操作。

因此，在阻力计算最优设置基础上，首先对非网格参数进行寻优，主要包括数值格式、湍流模型等。经过大量测试发现，相对于初始设置较大的偏差，更改非网格参数对计算结果的改善比较有限，改善幅度一般在3%以内。这说明，目前CFD 数值计算方法的成熟度较高，也侧面验证了所选的阻力模拟最优参数设置在非网格参数上的可靠性。

接着，对网格参数进行研究后发现：（1）背景网格加密对结果影响较小；（2）船体网格三个方向中（船长方向、船周方向、壁面方向），船长方向和壁面方向网格加密对计算结果影响较大，船周方向网格加密对结果影响较小。

由分离流动的特征可以推测，其对边界层的模拟或需要更高的网格分辨率。测试发现：（1）采用壁面函数时，第一层壁面高度偏大（对于阻力计算可能是合适的，因为分离流动小，且只关注阻力）；（2）不采用壁面函数，取Y+=1将大幅改善侧向力和摇艏力矩，但大攻角下的阻力偏差较大。

表2给出了船长方向和壁面方向网格加密的计算结果。其中，三个设置如下：

表2 KVLCC2偏航模拟不同船体网格设置计算结果偏差Tab.2 Error results of different grid settings for KVLCC2 obliquely towed test

①L150Y45——船长方向网格数为150，Y+=45（基础设置）

②L150Y1——船长方向网格数为150，Y+=1

③L300Y1——船长方向网格数为300，Y+=1

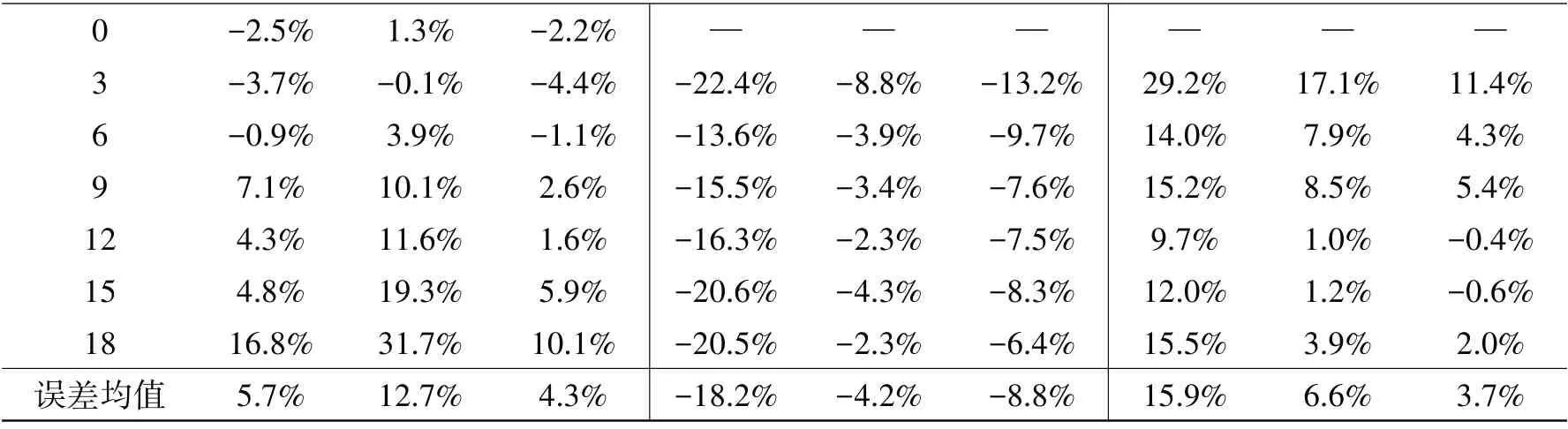
续表2

可以看到，相比于基础设置，L150Y1 设置对应的侧向力和摇艏力矩误差均有大幅改善：误差均值，侧向力由常规设置的-18.2%改善到-4.2%，摇艏力矩由常规设置的15.9%改善到6.6%。但纵向力CX偏差较大，平均偏差12.7%，18°攻角对应偏差达31.7%。

经测试发现，沿着船长方向加密网格将有效改善CX偏差，L300Y1 工况中，相比于L150Y1 工况，CX偏差大幅改善：误差均值由12.7%改善到4.3%，最大偏差由31.7%改善到10.1%。另外，摇艏力矩CN偏差有小幅改善，由6.6%改善到3.7%；侧向力CY偏差略有增加，由-4.2%变化到-8.8%。

图2 为12°偏航角时，船体首部的压力分布试验与不同设置计算结果比较。可以看出，加密边界层网格后，压力分布形式与试验基本相符。其中L150Y45工况可以看到压力存在振荡，说明边界层垂向网格分辨率不够，不采用壁面函数工况下（Y+=1），振荡消失。

图2 KVLCC2偏航船体表面压力分布（β=12°）Fig.2 Distribution of surface pressure coefficient for β=12°

前面的研究获取了针对本自主CFD 求解器的分离流动计算的最优参数搭配（见表3），后续将通过多子样应用做进一步验证。

表3 旋臂试验模拟最优参数搭配Tab.3 CFD best practice for rotating arm test

3 最优参数搭配的多子样验证

3.1 计算对象与工况

本文选取CSSRC 系列集装箱船（共8 条）展开研究，该系列船型在中国船舶科学研究中心旋臂水池进行了拘束模试验，系列集装箱船几何外形如图3 所示，主参数见表4。

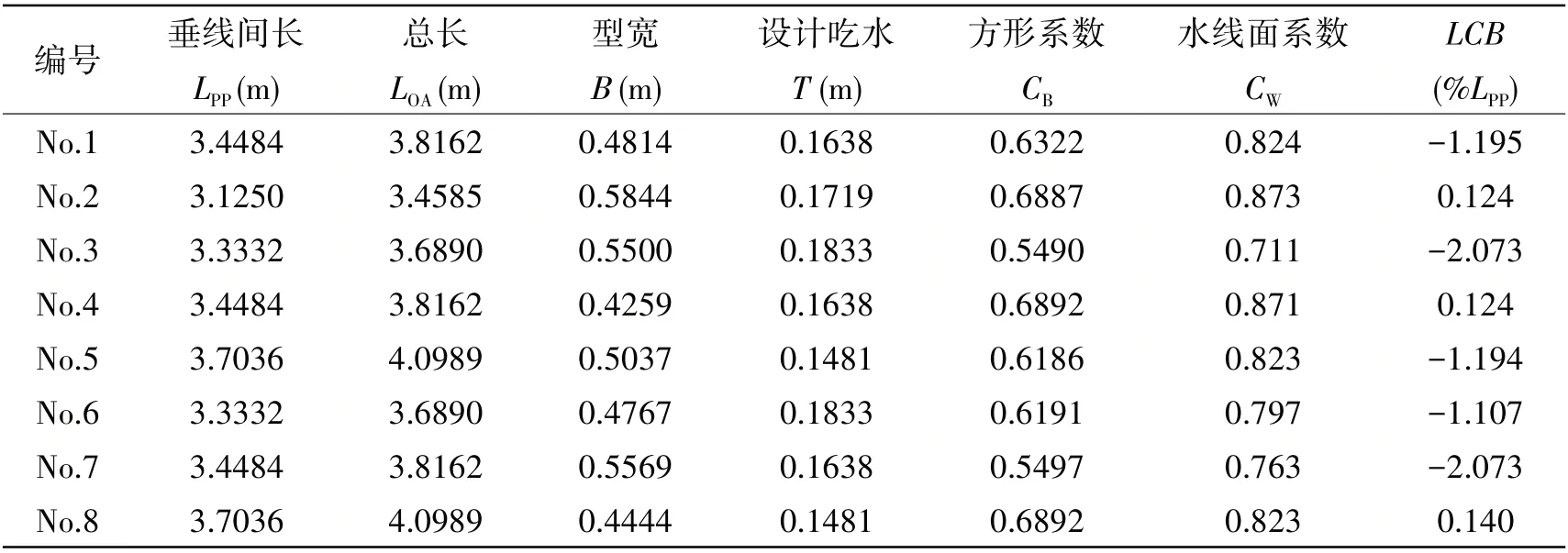
表4 CSSRC系列集装箱船模主参数Tab.4 Principal dimensions of the CSSRC container series

图3 CSSRC系列集装箱船几何外形示意图Fig.3 Hull forms of the CSSRC container series

计算工况描述：针对纯回转情况（漂角固定为0），选取4 个不同半径（R=10 m、12 m、15 m、20 m），进行了高速（Fr=0.25）和低速（Fr=0.16）两个航速的试验（取总长LOA作为特征归一长度），总计64 个工况（8×4×2=64，对称船型，理论上正转和反转结果呈反对称）。所有工况统一按表3中的参数设定进行计算，计算网格数为347.5万。

3.2 旋臂试验数值计算方法概述

旋臂试验需要让船模在水池中作圆周运动，CFD 数值计算中如何模拟这一圆周运动是一个关键问题。常规的模拟方法是仿照旋臂水池试验，建立一个很大的计算区域（比如圆柱或者圆环）来模拟试验水域以便让船舶在区域内做圆周运动；在处理船体网格相对运动上，可以采用MRF 多参考系方法或者滑移网格方法[15-16]。常规方法的缺点是：所需的计算域很大，导致网格数量增多；不同半径工况的计算域处理较麻烦。

本文采用的是基于ALE（Arbitrary Lagrange-Euler）的处理方法，聚焦于船体周围附近的流场，让背景网格跟随船体一起做圆周运动，这样只需在船体周围建立背景网格，不仅减小了计算网格数量，且可以很好地适应不同半径回转的工况。图4 为该方法模拟旋臂试验时不同相位的波形示意图。

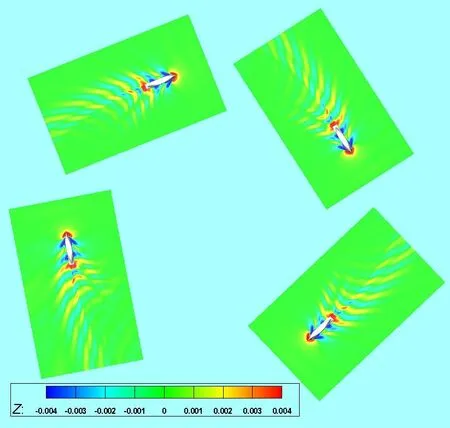
图4 ALE方法模拟旋臂试验时不同相位的波形示意图Fig.4 Simulation of rotating arm test using ALE method

3.3 计算结果

对于旋臂试验来说，通常侧向力系数的试验数据离散度较大，这主要是因为侧向力相对来说是一个小量，且容易受到回转离心力的影响，很难进行量化比较。因此本文重点针对回转力矩试验结果进行统计分析。

以No.1 船的结果为例，图5 为Fr=0.25 和Fr=0.16 对应的计算和试验结果比较图。其中CFD_R 表示采用阻力模拟最佳设置结果(表1)、CFD_M 表示采用寻优后的设置(表3)，EFD1 和EFD2 表示有两次重复试验结果。可以看到：采用阻力模拟最佳设置的曲线相对于试验有一个明显的偏离，而采用优化设置后，计算结果与试验吻合良好。

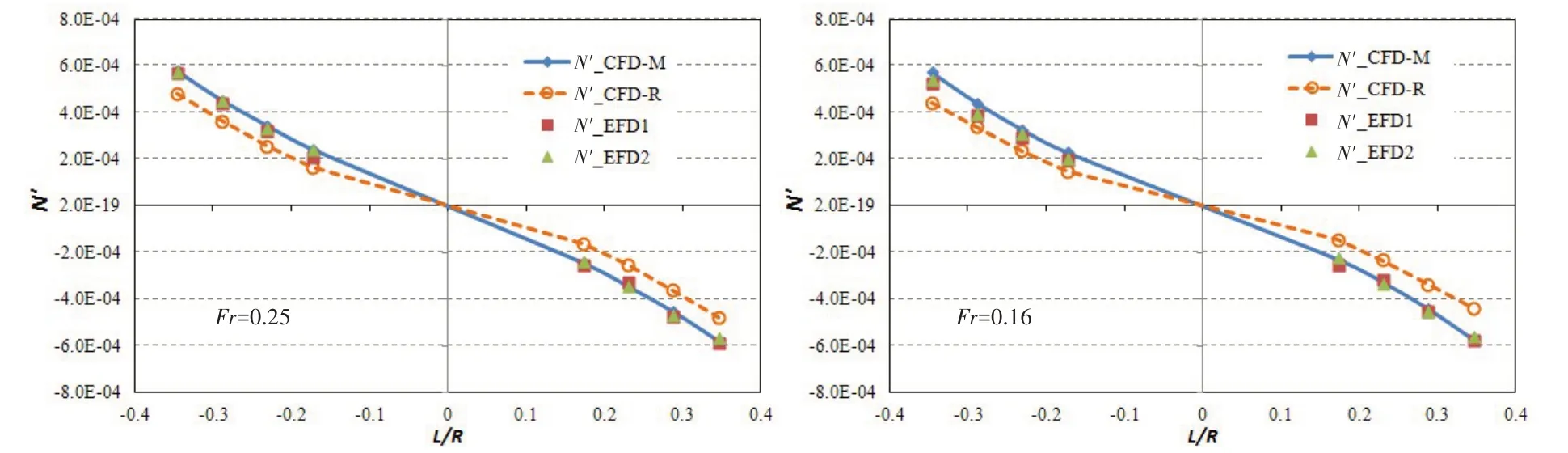
图5 No.1船在Fr=0.25和Fr=0.16时对应的N′计算与试验结果比较Fig.5 Comparison of N′for No.1 ship model when Fr=0.25 and Fr=0.16

经过No.1船的结果分析，初步验证了所提取的最佳参数搭配的有效性，接下来将针对系列船型展开多子样验证分析。表5为系列集装箱船纯回转工况旋转导数Nr′的误差统计，其中No.1_R表示阻力模拟最佳设置结果，其余为优化设置后的结果。可以看到，采用优化设置后，计算结果有了明显的改善，且大部分结果的误差在8%以内。

表5 系列集装箱船纯回转工况旋转导数Nr′误差统计Tab.5 Error statistics of Nr′on simulation of the CSSRC container series

图6为系列集装箱船纯回转工况旋转导数Nr′的误差概率统计图，总共16个样本点。可以看到：误差的概率分布大致呈正态分布；误差的统计平均值为1.79%，标准方差为5.05%；其中，误差绝对值小于8%的样本占比为93.8%。

图6 旋转导数Nr′误差概率分布Fig.6 Probability distribution of errors on Nr′

图7 为系列集装箱船纯回转工况水动力系数N′的误差概率统计图，总共64 个样本点，是旋转导数样本点的4倍（一个旋转导数的获取需进行4个半径的试验）。可以看到：误差的概率分布大致呈正态分布，且相比于旋转导数的统计曲线更光顺；误差的统计平均值为3.96%，标准方差为4.79%；其中，误差绝对值小于10%的样本占比为92.2%。

图7 水动力系数N′误差概率分布Fig.7 Probability distribution of errors on N′

4 结 语

本文分析了对标典型工况所获得的CFD 最佳参数搭配推广到新工况过程中的信任传递过程，引入离散样本空间的概念尝试，从理论上描述大子样验证的实践；同时针对操纵性拘束模试验中开展的相对较少的旋臂回转试验，以8 条CSSRC 系列集装箱船的物理试验数据为基础展开相关验证研究。对总计16 个样本点的旋转导数Nr′的误差概率进行了分析，结果显示：误差的概率分布呈类正态分布；误差的统计平均值为1.79%，误差绝对值小于8%的样本占比为93.8%；在相应的总计64 个样本点的水动力系数N′的误差概率分析中，误差的概率分布呈类正态分布，且相比于旋转导数的统计曲线更光顺，误差的统计平均值为3.96%，误差绝对值小于10%的样本占比为92.2%；数值实践结果进一步证实了“大子样验证”思路在流动复杂、子样较少情况下的有效性。