基于误差融合的自导鱼雷发现概率解析方法研究*
张祥甫,闫少坤
(1. 海装驻连云港地区军代室,江苏 连云港 222061;2. 江苏自动化研究所,江苏 连云港 222061)
鱼雷的发现概率是反映鱼雷攻击效能的关键量化指标,它不仅与鱼雷的战术技术性能指标有关,而且与作战使用方法、攻击对象属性、发射平台有关系统性能乃至海域水文条件等多因素密切相关。
计算自导鱼雷发现概率主要有蒙特卡洛法和解析法。蒙特卡洛法,又称为模拟法。模拟法的优点是结构简单,需要模型解析结构的知识较少,且可以真实地仿真各种水文条件、鱼雷复杂的环形、蛇形搜索、目标机动等各种复杂情况。蒙特卡洛法存在计算速度慢的缺点,如为达到满意的计算精度,可能需要成百倍地增加同一条件下的仿真次数;其次,同一条件下的不同仿真次数一般总有波动,计算的等概率线一般不光滑,不利于最优占位与机动等问题的算法研究。解析计算法针对直航搜索鱼雷等雷目运动关系比较明确的情况,可以快速准确地在线评估,得到准确的发现概率,但对于目标机动或鱼雷非直航搜索等运动关系不确定的情况,使用解析法很难得到准确结果。针对鱼雷发现概率的计算问题,国内的学者做了大量的研究,取得了丰硕的成果。
本文重点讨论了基于误差融合的自导鱼雷发现概率解析计算方法,通过仿真研究了不同边界条件对仿真结果的影响。结合蒙特卡洛法的仿真结果,证明了解析模型的正确性。
1 声自导鱼雷发现概率解析法计算模型
1.1 声自导鱼雷射击阵位关系
在鱼雷性能一定的条件下,自导鱼雷的发现概率是射击条件和提前角的函数,当射击条件一定时,则以提前角体现出对发现概率的影响。本节利用有利提前角计算声自导鱼雷的发现概率,当鱼雷以有利提前角所确定的航向航行时,鱼雷与目标相遇是指自导扇面的形心与目标相遇。在不考虑目标机动以及声诱饵和干扰器材等影响的条件下,相应的射击阵位关系如图1所示。
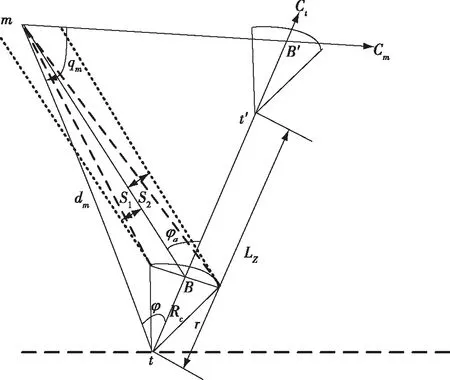
图1 有利提前角射击阵位关系图
图1中、、、分别表示目标、鱼雷及其初始航向;为攻击初始时刻雷目距离;和分别表示正常提前角和有利提前角;表示自导扇面的形心到雷头的距离;表示自导扇面的半径;表示敌弦角;表示直航搜索段航程;和表示过自导扇面边缘与目标相对位移线平行的两线,其与目标相对位移线的距离。
形心提前角法推导公式如下:
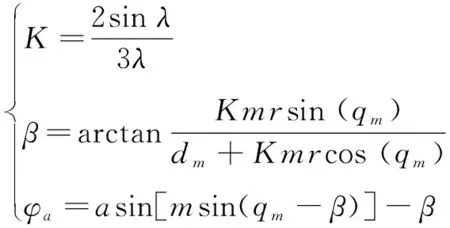
(1)
其中:表示常系数;表示声呐识别扇形半角;表示相对移动极限角角平分线与雷目连线夹角;表示目标与鱼雷速度的比值;表示扇面半径;表示初始位置目标弦角;表示有利提前角。
声自导鱼雷发现概率的求解需要先求得直航搜索段航程,当鱼雷以有利提前角射击时,根据图1中的阵位关系求得直航搜索段航程。

(2)
其中,表示自导鱼雷发现目标时的弦角。
根据有利提前角的定义,当=时,鱼雷发现目标的概率最大,此时的提前角就是有利提前角。通过对射击阵位关系进行推导分析,求得和的计算公式如下。
=*sin+*sin(--)
(3)
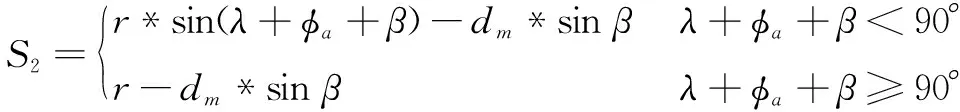
(4)
1.2 声自导鱼雷发现概率求解
假设测量误差均符合正态分布,发现概率计算公式如下
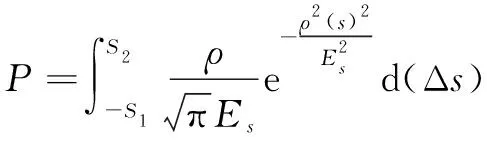
(5)
其中,=047694,为综合概率误差。
对发现概率公式进行拉普拉斯变换,结果表示如下
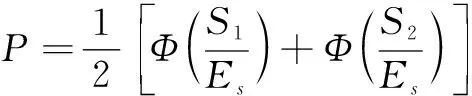
(6)
2 尾流自导鱼雷发现概率解析法计算模型
2.1 尾流自导鱼雷射击阵位关系
与声自导鱼雷不同的是,尾流自导鱼雷的期望命中点在有效尾流与目标长度和的中点处,只要鱼雷进入尾流点在有效尾流的范围内则认为鱼雷发现目标,相应的射击阵位关系如图2所示。
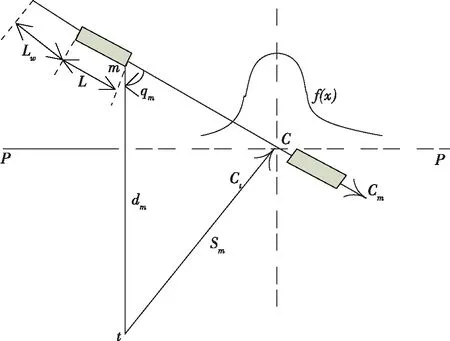
图2 尾流自导鱼雷射击阵位关系图
图2中,表示有效尾流的长度;表示目标舰船的长度;表示积分投影线;()表示发现概率密度函数;点表示期望的命中点;表示鱼雷的航程。
2.2 尾流自导鱼雷发现概率模型
类似于声自导鱼雷,尾流自导鱼雷既有目标位置散布,也有鱼雷位置散布。假设目标位于(,+)范围内的概率为,在目标位于的条件下鱼雷发现目标的概率为,因此目标在该范围内又恰好被发现的概率计算如下
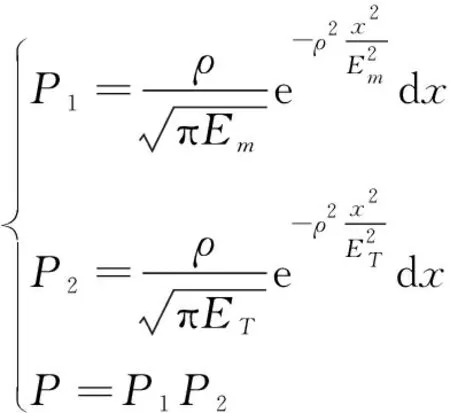
(7)
其中,表示目标运动要素误差;表示鱼雷航行误差。
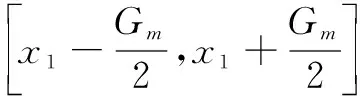
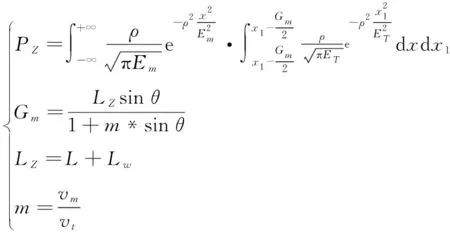
(8)
其中,表示单发雷的发现概率;表示单发鱼雷命中间隔;表示有效尾流和目标的总长度;表示目标速度与鱼雷速度的比值;表示尾流鱼雷的进入角。
3 射击误差融合模型
鱼雷的射击误差主要考虑目标运动要素误差和鱼雷航行误差。其中,目标运动要素误差包括敌速误差、敌弦角误差、射距误差、瞄准误差;鱼雷航行误差包括鱼雷速度误差、鱼雷航向误差。而求解概率误差的方式有投影法和灵敏度法,本文采用投影法求解综合概率误差,相应的求解公式如下。
3.1 声自导鱼雷综合概率误差
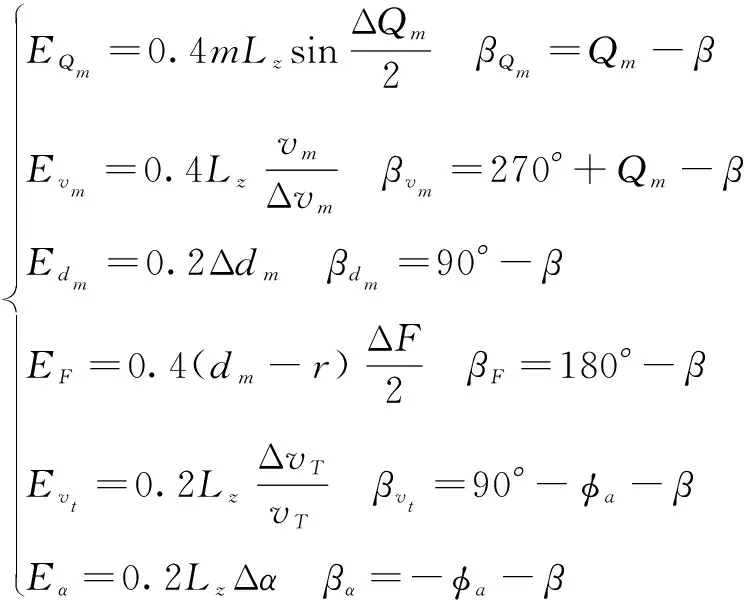
(9)
以上各项误差前四项组合可求得目标散布概率误差,后两项可合成鱼雷散布概率误差。将目标散布误差和鱼雷散布误差合并成综合概率误差
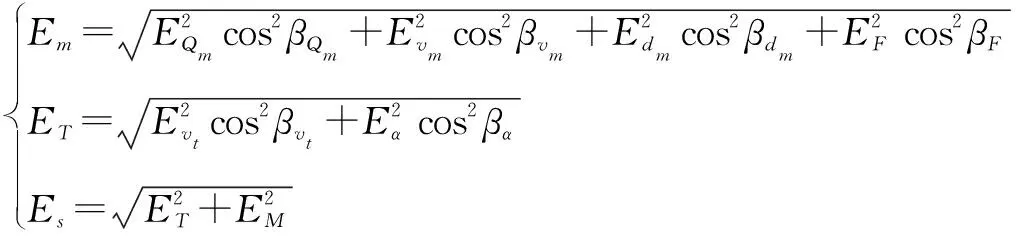
(10)
3.2 尾流自导鱼雷综合概率误差
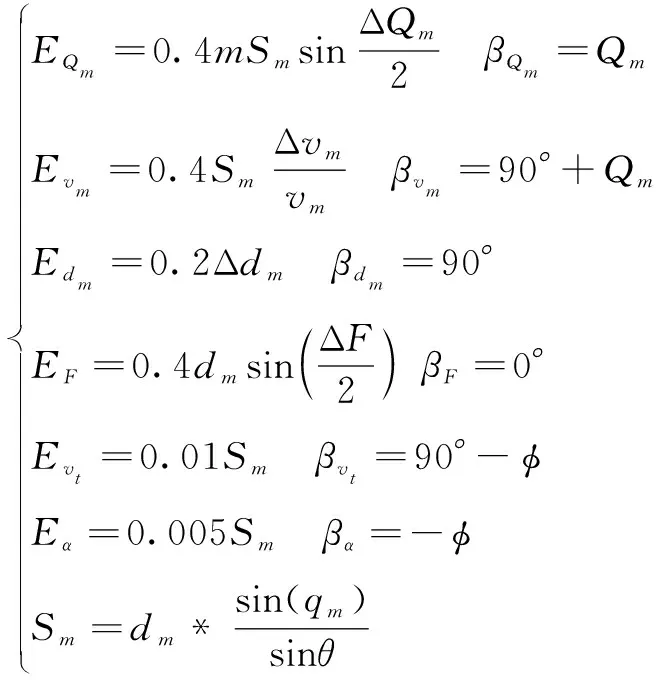
(11)
采用投影法将尾流自导鱼雷的误差融合,前四项组合可求得目标散布概率误差,后两项可合成鱼雷散布概率误差。将目标散布误差和鱼雷散布误差合并成综合概率误差:
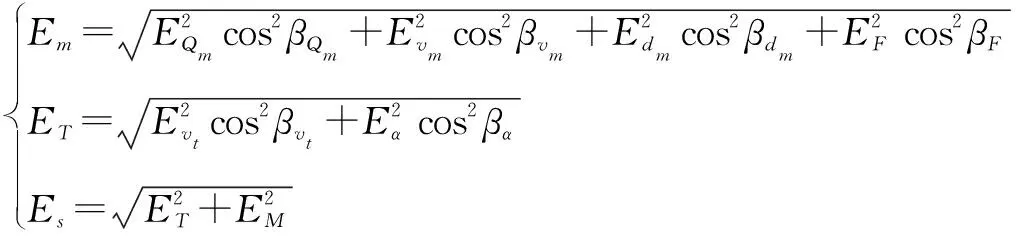
(12)
4 仿真结果
为了验证声自导解析法模型和尾流自导解析法模型的正确性,在相同的态势下,比较上述模型的计算结果和蒙特卡洛法的仿真结果;在其他条件一定时,研究不同参数变量对鱼雷发现概率的影响。
4.1 声自导模型验证结果
设定声自导鱼雷自导扇面的半径=200 m,扇面半角=20°,目标速度=15 kn,初始距离=10 km,敌弦角=30°,蒙特卡洛法仿真1 000次,在不考虑鱼雷航程有限的前提下,研究不同鱼雷速度对发现概率的影响结果如图3所示。
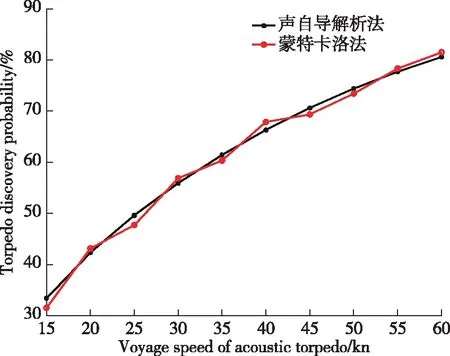
图3 声自导鱼雷发现概率随鱼雷速度变化曲线
由图3可知,在其他条件一定时,随着鱼雷的航行速度增加,声自导鱼雷的发现概率逐渐升高,且增高的速度逐渐变缓。主要原因是鱼雷追击目标前期,鱼雷的速度是主要影响因素,追击后期受到其他因素条件的限制。图中声自导解析法与蒙特卡洛法的仿真结果相差在3%以内,证明了声自导解析法模型的正确性和可行性。
设定声自导鱼雷自导扇面的半径=200 m,扇面半角=20°,目标速度=15 kn,初始距离=10 km,鱼雷速度=20 kn,蒙特卡洛法仿真1 000次。在不考虑鱼雷航程有限的前提下,研究不同敌弦角对发现概率的影响结果如图4所示。
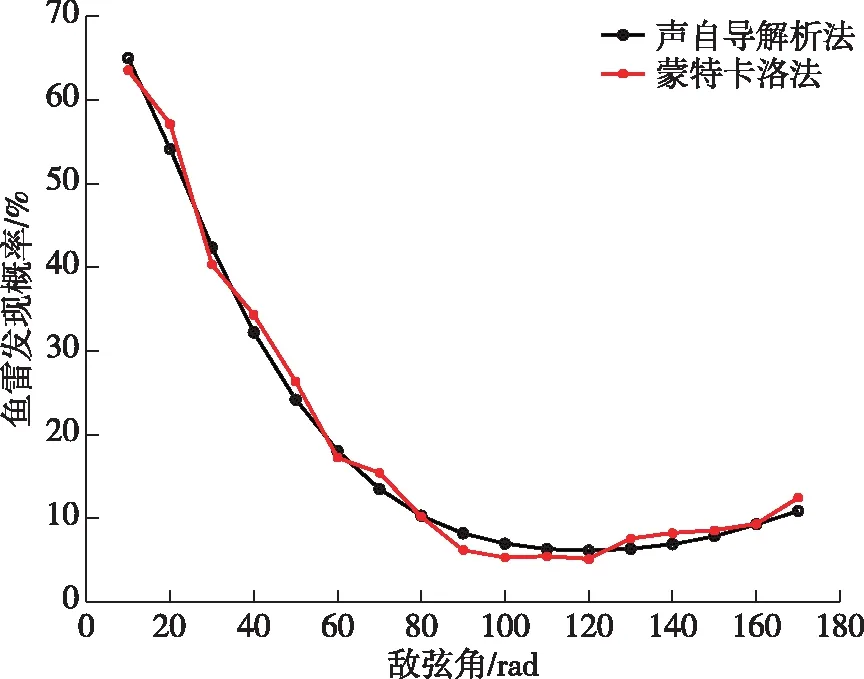
图4 声自导鱼雷发现概率随敌弦角变化曲线
由图4可知,在其他条件一定时,随着鱼雷的敌弦角增加,声自导鱼雷的发现概率先逐渐降低再逐渐升高,且升高趋势很缓慢。主要原因是起始阶段随着敌弦角的增加,相遇点距离初始位置变大导致鱼雷发现概率降低;当敌弦角超过某一值时,可以近似看作追击问题,发现概率受速度的影响较大。图中声自导解析法与蒙特卡洛法的仿真结果相差在3%以内,证明了声自导解析法模型的正确性和可行性。
设定声自导鱼雷自导扇面的半径=200 m,扇面半角=20°,目标速度=15 kn,敌弦角=30°,鱼雷速度=20 kn,蒙特卡洛法仿真1 000次。在不考虑鱼雷航程的前提下,研究不同雷目距离对发现概率的影响结果如图5所示。
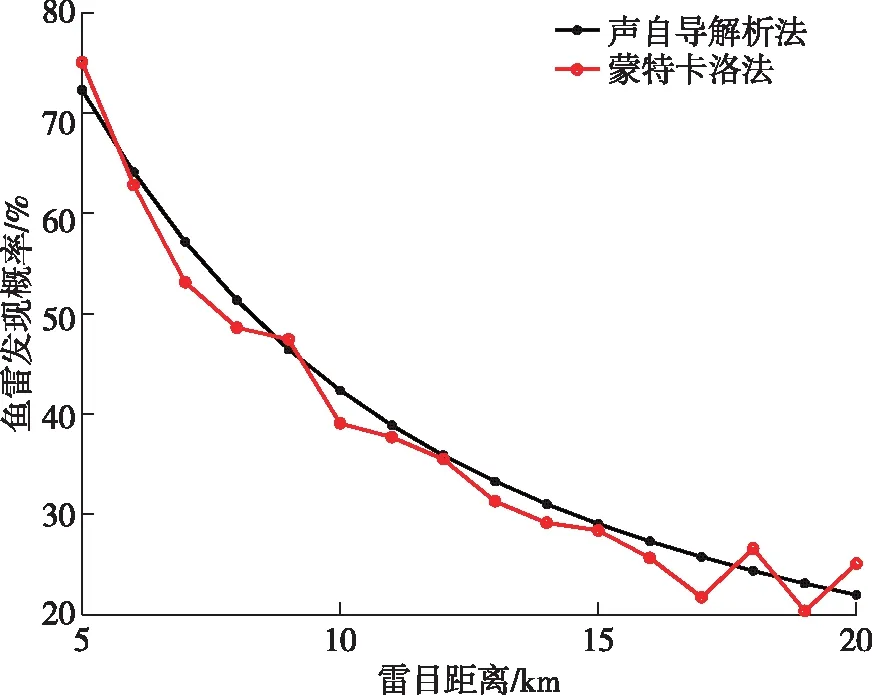
图5 声自导鱼雷发现概率随雷目距离变化曲线
由图5可知,在其他条件一定时,随着雷目距离增加,声自导鱼雷的发现概率逐渐降低,符合预期。且图中声自导解析法与蒙特卡洛法的仿真结果相差在3%以内,证明了声自导解析法模型的正确性和可行性。
4.2 尾流自导模型验证结果
设定有效尾流和目标舰船总长度+=2 000 m,目标速度=15 kn,敌弦角=30°,初始距离=10 km,蒙特卡洛法仿真1 000次。在不考虑鱼雷航程的前提下,研究不同鱼雷速度对发现概率的影响结果如图6所示。
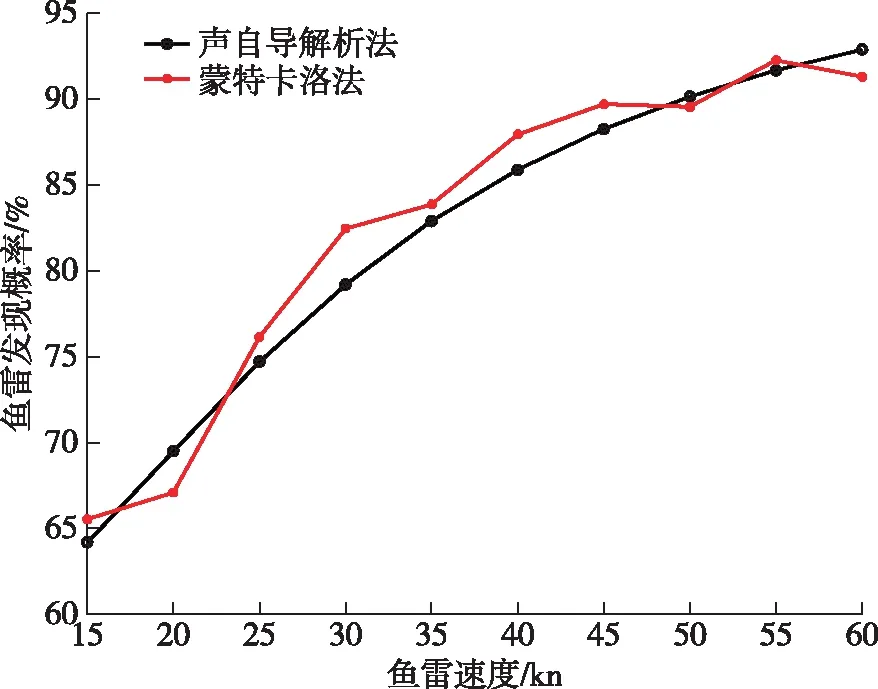
图6 尾流自导鱼雷发现概率随鱼雷速度变化曲线
由图6可知,在其他条件一定的情况下,随着尾流自导鱼雷速度的增加,鱼雷发现目标的概率逐渐增加,且增加速度变缓。主要原因是由于导引后期鱼雷速度不再是主要影响因素。图中尾流自导解析法和蒙特卡洛方法的结果变化趋势一致,误差在4%左右,证明尾流自导解析法模型的正确性。
设定有效尾流和目标舰船总长度+=2 000 m,目标速度=15 kn,初始距离=10 km,鱼雷速度=20 kn,蒙特卡洛法仿真1 000次。在不考虑鱼雷航程的前提下,研究不同敌弦角对发现概率的影响结果如图7所示。
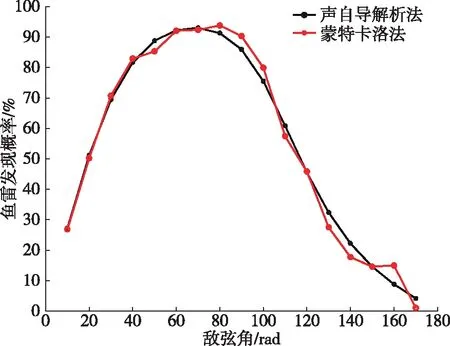
图7 尾流自导鱼雷发现概率随敌弦角变化曲线
由图7可知,在其他条件一定时,随着敌弦角的增加,鱼雷发现概率先变大后变小。主要原因是射距一定时,敌弦角过小雷目运动近似相向运动,敌弦角过大相当于追击问题,鱼雷进入有效攻击长度中点附近的概率降低。图中尾流自导解析法和蒙特卡洛方法的结果变化趋势一致,误差在4%左右,证明尾流自导解析法模型的正确性。
设定有效尾流和目标舰船总长度+=2 000 m,目标速度=15 kn,敌弦角=30°,鱼雷速度=20 kn,蒙特卡洛法仿真1 000次。在不考虑鱼雷航程的前提下,研究不同初始距离对发现概率的影响结果如图8所示。
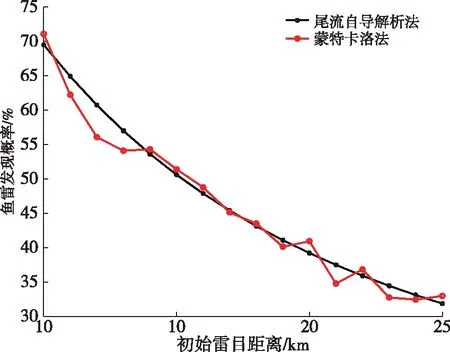
图8 尾流自导鱼雷发现概率随雷目距离变化曲线
由图8可知,在其他条件一定时,随着雷目距离的增加,尾流自导鱼雷发现目标的概率逐渐降低,和预期一致。图中尾流自导解析法和蒙特卡洛方法的结果变化趋势一致,误差在4%左右,证明尾流自导解析法模型的正确性。
5 结束语
本文提出了基于误差融合的自导鱼雷发现概率计算模型,解决了自导鱼雷发现概率解析法实时计算的难题。在相同态势下,通过与蒙特卡洛方法对比,分析了鱼雷速度、敌弦角、雷目距离等边界条件对自导鱼雷发现概率的影响,证明了本文所提模型的正确性和有效性。本文模型主要解决目标和鱼雷匀速直线运动条件下的发现概率计算问题,而真实战场环境瞬息万变,目标潜艇或舰船会随时机动且采取软硬对抗措施以规避鱼雷,后续将会研究动态环境下基于对抗策略的自导鱼雷发现概率实时计算问题。

