基于等效体积法的含缺陷海底管道完整性失效判据研究*

方卓钰 董绍华 古青 段宇航 彭东华 谢书懿 孙伟栋， 刘保余

1中国石油大学（北京）管道技术与安全研究中心

2中国石油集团渤海钻探工程有限公司

3中石化长输油气管道检测有限公司

海洋环境复杂多变，海底管道在运输油气的过程中不可避免地会产生损伤[1-3]，常见的海底管道缺陷类型主要包括腐蚀缺陷和外部机械损伤（船锚刮伤等），当缺陷程度严重时，可能会导致海底管道发生破裂。一旦油气泄漏到海洋之中，不但严重危害海洋环境，还将导致火灾、爆炸等事故，造成巨大的经济损失，所以对海底管道的失效安全评定工作进行深入的研究具有重要意义。

近年来，国内外学者应用有限元对含缺陷管道的失效分析进行了大量研究，HU等[10]应用有限元研究了长缺陷管道的极限内压在复合载荷作用下的变化情况，并结合可靠性方法对海管进行安全评定；黄宇立等[11]通过有限元对含缺陷海底管道进行应力分析，并应用许用应力法对单缺陷海管进行安全评估；XIA等[12]基于有限元模型详细研究了缺陷的长度、宽度、深度、压力载荷和轴向力对管道剩余强度的影响；杨培[13]应用拉伸试验得到应力—应变曲线，基于ABAQUS模拟数据，得到适用于X52钢材的无限长缺陷管道失效压力的计算公式；张足斌等[14]应用响应曲面法回归出缺陷参数与管道剩余强度之间的关系式。但是在以往的研究中没有考虑失效判定准则的局限性，所研究出的失效压力预测公式大多没有考虑缺陷的长度对公式的影响或只适用于含轴向长缺陷管道，并且缺乏对X60海底管道的研究和分析。

在前人研究的基础上，本文使用ANSYS WORKBENCH 仿真软件进行模拟，以X60 直缝埋弧焊海底管道作为研究对象，讨论出更适合X60管道的失效评定方法。为了改善现有失效判定准则的局限性，研究了缺陷参数对管道失效模式的影响，并计算出70 组含缺陷X60 海底管道失效时等效应力超过抗拉强度的相对体积，得到一种基于等效体积法的含缺陷海底管道完整性失效判据，可以对管道的失效条件进行定量的判定。基于新判据模型和73 组有限元数据，以缺陷长度为基准拟合出两种适用于含缺陷X60管道的失效压力计算模型。以文献中的真实爆破试验数据验证了模型的正确性，进而验证了判据的适用性，从而为含缺陷管道的失效研究提供了新思路和新的理论参考，为有限元模拟提供了初步的判断依据。

1 有限元模型

1.1 管道工作载荷的施加

管道在运输的过程中，会受到多种作用力的影响。由于管体受端部效应的影响，沿管道的轴线方向往往会有轴向力的作用，管道本身由于输送介质受到的内压载荷影响，在模拟的过程中，所建立的模型相较于真实的海底管道长度很小，所以设定管道所受到的轴向力为恒定数值。内压载荷采取在某时间内进行线性加压的方式均匀施加在模型的内表面。

1.2 几何模型的构建与边界条件的确定

由于缺陷形状复杂，在有限元分析中需要将其进行简化为规则形状，在简化过程中，最重要的是需要确定缺陷的长度[5]。对于不规则形状的缺陷可以采用平均值方法进行简化，即将缺陷形状简化为外部和内部最大尺寸的矩形，最后缺陷的长度可以近似为两个矩形长度的均值，缺陷形状可以转化为矩形形状。所以，本文重点研究平底矩形缺陷对海底管道剩余强度的影响。为减少边界条件对模拟结果的影响，节省有限元模拟时间，取1/4 管段进行建模，设置合适的管道长度，从而减小边界条件对缺陷及其周边的影响[15]。管道在实际运行中被海底土壤约束，所以需要在模型端面施加对称约束，1/4 管道的轴向平面和缺陷所在的横向截面也都需要设置对称的边界条件。为避免管道模型在计算的过程中出现刚体移动的现象，应在管道模型横向截面的位置施加轴向位移约束。由于管道的缺陷及其周边处应力、应变梯度较大，为准确研究该处的应力分布，采用细小的60 节点六面体单元SOLID186网格划分该处，所以缺陷的大小不同，所划分的六面体单元的区域也有所不同。经验证：当单元尺寸为2 mm 时，不但能满足精度要求，还能节省计算时间，剩余管体部分则采用大网格进行扫略划分，划分结果如图1所示。在建模时，对缺陷周围进行倒角操作以避免缺陷附近出现应力集中现象。

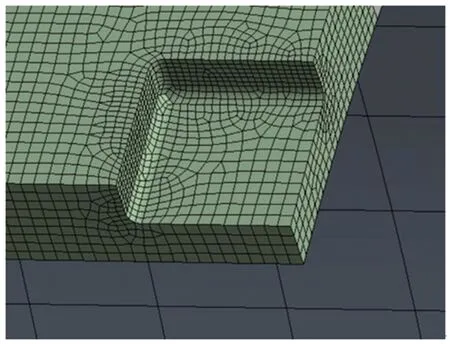
图1 缺陷处有限元模型Fig.1 Finite element model of the defect

1.3 管材特性

依据标准《ASTM A370—18》对管材取样，进行拉伸性能试验。在环焊缝处取样，选取X60海底管道管体90°横向的矩形板拉试样，室温下做三组实验，将所有试样单轴拉伸至断裂，最后得到材料的屈服强度为476.33 MPa，拉伸强度为602.67 MPa，断后伸长率均为42%，弹性模量2.07 GPa，泊松比0.3。通过式（1）和式（2）可以获得管材试样的真实应力—应变曲线[16]（图2）。在有限元中需要使用弹塑性本构模型描述管材的应力—应变关系，即使用管材的真实应力和塑性应变。由于颈缩断裂阶段的数据对计算结果影响不大，所以不再考虑抗拉强度以上的应力、应变关系。

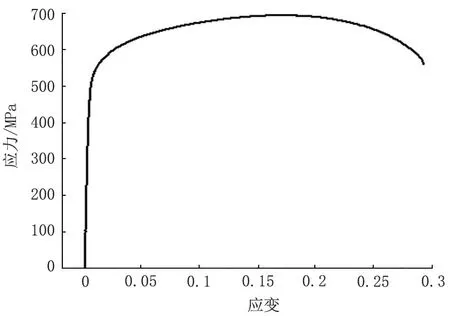
图2 真实应力—应变曲线Fig.2 True stress-strain curve

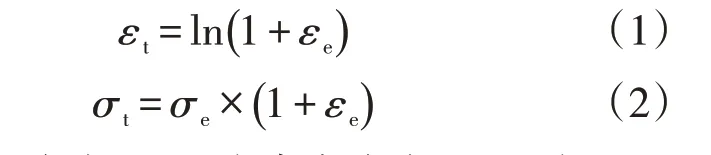
式中：εe为工程应变；εT为真实应变；σe为工程应力，MPa；σT为真实应力，MPa。

1.4 缺陷管道的真实爆破压力

截取一段整管进行缺陷管道的水压爆破试验，缺陷管道的缺陷尺寸为50 mm×50 mm×8.75 mm，为了得到更准确的两组管道试样的环向、轴向应力，在距离缺陷的四条边50 mm 处分别贴上应变片，水压爆破试验是在静水压试验之后进行，试验的温度为室温。经过重复的分阶段加压、保压操作至管道发生爆破，保压的时间均为10 min，保压压力均为17 MPa，最后得到管道的失效形貌（图3），缺陷管道爆破压力为28.24 MPa。缺陷管道的试验数据可以作为有限元研究的对照依据来检验准确性。

图3 缺陷管道试样爆破后形貌示意图Fig.3 Schematic diagram of the appearance of the defective pipe sample after blasting

1.5 失效判定方法的比较

塑性垮塌[17-18]是压力容器领域中单调递增加载的失效模式，在加载过程中共分为弹性、局部塑性变形，整体塑性变形和最后垮塌四个阶段，垮塌载荷属于垮塌阶段，是判定管道发生垮塌失效的参考载荷。该失效模型认为，当内压载荷施加到一定数值时管道的Von Mises 曲线发散时对应的内压载荷即为管道的失效压力，通过使用有限元计算的失效压力为30.10 MPa，对应的极限等效应力载荷即为垮塌载荷（665 MPa）。

钛合金是代替钢铁最有潜力的轻量化材料，各方面性能均占优势，唯一缺点在于价格过高，因此，对于钛合金的研究首先要集中在如何降低成本这一问题上[27].

实践过程中，获得管材的SMYS 和SMTS、以及每段管道的极限拉伸强度较为困难[19]，为了便于分析，对应用管材的屈服强度和抗拉强度进行失效的判定。针对不同钢级的管材应选用不同的参考应力[20]，使用常见失效判定方式达到相应参考应力时的失效压力可以通过有限元计算得到，采用屈服强度作为参考应力的方法得到的结果为9.10 MPa，采用抗拉强度作为参考应力的方法得到的结果为23.15 MPa。从对比真实数值28.24 MPa来看，使用塑性垮塌失效模型判定方法更准确，相对误差仅为6.586%。当管道发生塑性垮塌时，缺陷处的最小等效应力值小于抗拉强度，即没有达到抗拉强度时即失效，所以塑性垮塌模型最适用于该管道的失效评定。虽然该模型得到的结果更为准确，但是无法对含缺陷管道的失效条件进行定量的描述。

2 基于等效体积的管道失效评价

2.1 等效体积的计算及失效判定方法的建立

通过计算，当发生塑性垮塌时，相对于模型总体积已有0.45%等效体积的等效应力达到了抗拉强度，超过99.90%等效体积的等效应力超过了屈服强度。对比其他失效准则，当认为失效时只有缺陷局部处发生了屈服。所以塑性垮塌失效模式可以使得管道被最大限度地使用，更符合实际情况。当管道失效时等效应力超过抗拉强度的等效体积与缺陷体积的比值为25.839，证明了塑性失效准则具有一定的局限性，所以应该是当等效应力超过抗拉强度的等效体积达到一定数值时，才可认为管道失效，应用两种失效判定方法得到的应力云图如图4 所示。模拟时所划分的网格精度已保证得到的各应力区域为管道发生塑性垮塌时相应的弹塑性区域。缺陷处倒角部分的体积很小，为模型总体积的0.000 002%，并且也已进行单元的划分，所以可以忽略倒角大小对应力区域的影响。

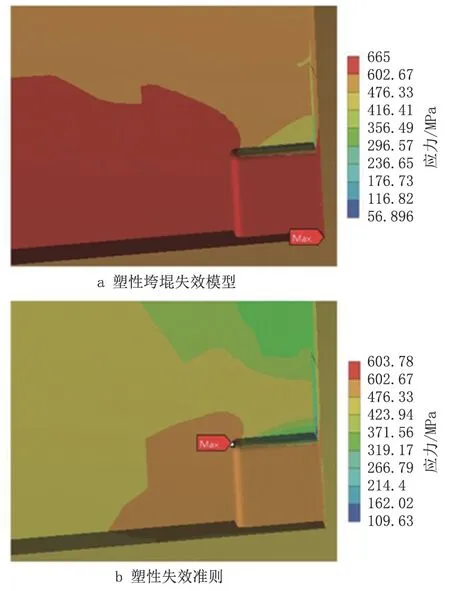
图4 分别使用塑性垮塌失效模型和塑性失效准则判定失效时的应力云图对比Fig.4 Comparison of stress cloud chart when using plastic collapse failure model and plastic failure criterion respectively to determine failure

通过对载荷子步对应的应力云图进行分析，发现当管道承压较小时，管道处于弹性阶段，最大等效应力随内压呈线性增长。当压力增大到一定程度时，缺陷及其部分周边区域率先进入屈服状态，其中缺陷边缘处为最大等效应力点，随后缺陷附近管体相继发生屈服。内压继续增大，缺陷区域进入屈服强化阶段，从外壁向内壁发展，整个管体也相继进入屈服阶段，临近垮塌时，最大等效应力位置处于缺陷的中心处。

通过使用塑性垮塌失效模型，得到含缺陷管道失效时的应力云图，使用有限元计算70 组含平底矩形缺陷管道失效时应力区域的等效体积比，计算结果如表1所示。大量的研究表明，缺陷的宽度对失效压力的影响较小，可以忽略，所以在计算时控制缺陷的宽度为恒定值[10，21]。尺寸参数深度、长度常用的表示方法为[4]，分别用k1、k2表示。可以发现，当缺陷的长度、深度数值较小时，管道失效时等效应力大于屈服强度的等效体积常常能占模型等效体积的90%以上，表示整个管体都进入了屈服状态，垮塌形式为整体垮塌。而随着缺陷长度、深度的增加，大于屈服强度的等效体积占比变得很小，所以可以推断含不同尺寸缺陷管道的失效模式不同。即：当缺陷的长度、深度数值较小时，管道的失效模式为整体失效；而当缺陷的长度、深度数值较大时，完好管体的等效应力值较小，处于弹性阶段，缺陷及其周边区域等效应力超过屈服强度，处于塑性阶段，此时管道局部失效，垮塌形式为局部垮塌。

并且可以发现，在大多数情况下，其他条件相同时，随着缺陷长度、深度的增加，管道失效时等效应力大于抗拉强度的相对体积越小，说明管体表面损伤越严重，管道越容易失效，并且缺陷深度对等效体积占比的影响大于缺陷长度对等效体积占比的影响。随着深度的加深，缺陷管道的失效形式变化越大，而当缺陷长度增加到一定程度时，缺陷管道失效时等效应力超过抗拉强度的相对体积数值基本不变。

由于管材的抗拉强度在工程上的应用更为广泛，所以在判据中应用管材的抗拉强度。为了对应用最为广泛的塑性失效准则进行补充，以及弥补塑性垮塌失效模型不能进行定量失效描述的不足，重点关注管道失效时等效应力超过抗拉强度的管体部分，以此得到一种基于等效体积法的含缺陷海底管道完整性失效判据。通过模拟发现，当缺陷的体积非常小时，管道失效时大部分管体的等效应力均已超过抗拉强度。由于在模拟过程中，模型本身的长度有限，此时难以定量计算该部分等效体积的确定值，并且在实际运行过程中，应重点关注较大体积缺陷对管道剩余强度的影响，所以本文所研究的失效判据主要针对当管体失效时管体局部等效应力大于抗拉强度时的情况，此时缺陷对于海管正常运行的影响更需要重点研究。表1中计算出了每一组缺陷管道失效时等效应力大于抗拉强度的等效体积与缺陷体积的比值。

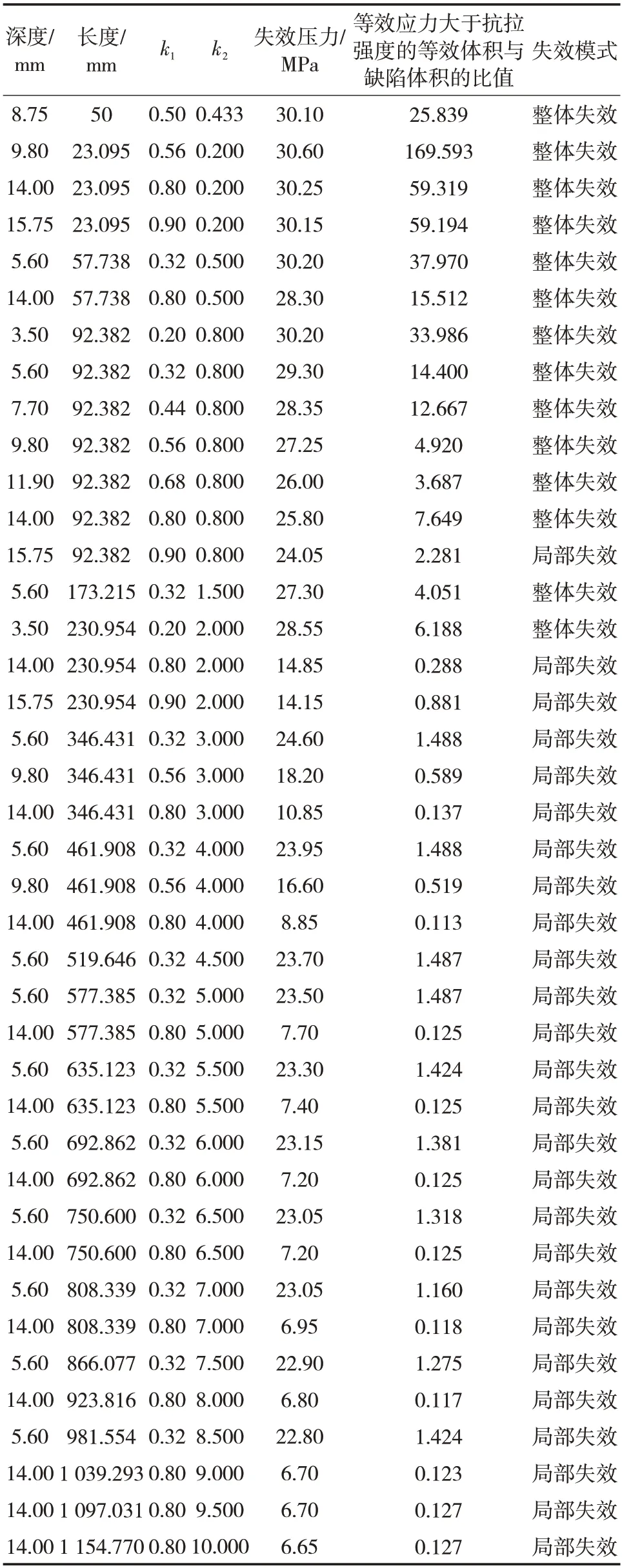
表1 70组缺陷管道失效后的计算结果Tab.1 Calculation results after failure of 70 groups of defective pipelines

大多数学者采用参数函数拟合法得到剩余强度的相关公式，冯明洋[5]提出了多项式拟合法，拟合结果为两个由k1，k2组成的因式乘积，本文采用多项式拟合法进行模型的构建。同时引入抗拉强度和垮塌载荷，运用最小二乘法进行拟合，最终得到基于等效体积法的含缺陷海底管道完整性失效判据如式（3）所示，从而提出适用于X60 海底管道失效判定的新方法。利用该判据，可以得到含不同尺寸缺陷等效应力大于抗拉强度的相对体积，从而得到不同缺陷存在时管道的定量失效条件。可以发现，模型的相关系数的平方约为0.990，模型准确度较高，且形式具有较强的规律性，便于应用和推广。

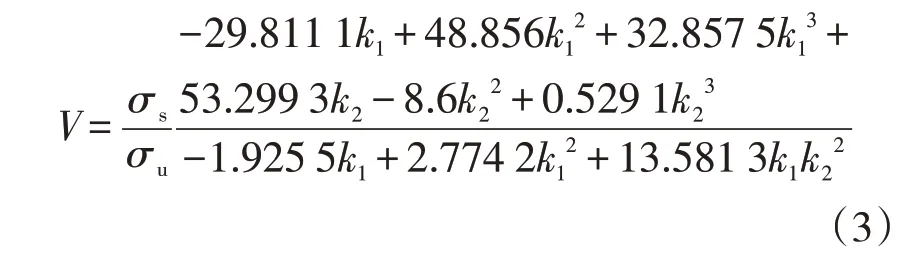
式中：V为管道失效时等效应力大于抗拉强度的相对体积；σs为垮塌载荷，MPa；σu为抗拉强度，MPa；k1为缺陷的相对深度；k2为缺陷的相对长度。

对比使用有限元方法得到的相对体积和拟合公式得到的相对体积可以发现（图5），两者结果非常相近。

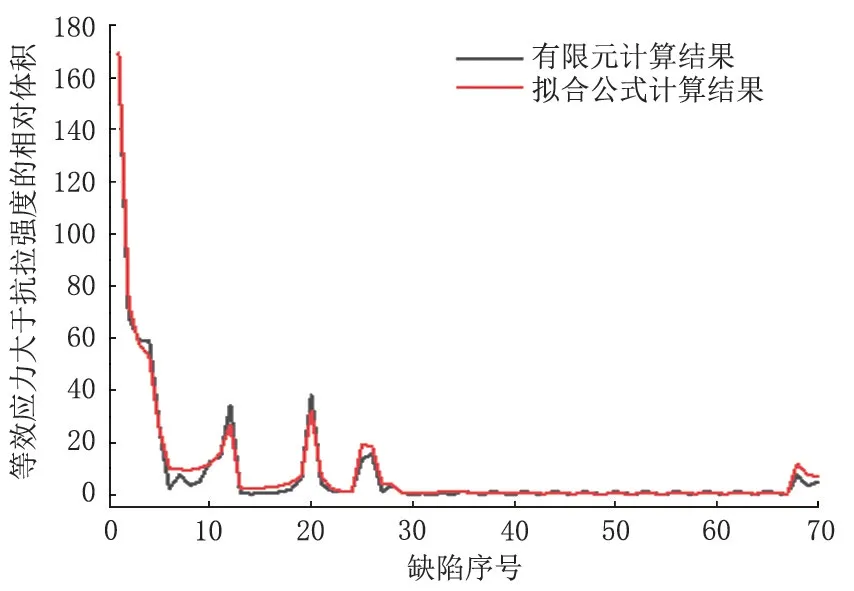
图5 X60海底管道有限元和拟合公式得到的等效应力相对体积对比曲线Fig.5 Comparison curve of equivalent stress relative volume obtained by X60 submarine pipeline finite element and fitting formula

2.2 失效压力计算模型

2.2.1 模型建立

通过上述模型式（3）得到X60 海管的失效条件，需要找出判据与失效压力之间的关系，构建失效压力计算模型，通过验证该模型的准确性进而验证失效判据的适用性。陈严飞[4]认为，随着缺陷长度的增加，长度对管道失效压力的影响越来越小，所以可以依据缺陷的长度进行分段回归，得到更准确的海底管道失效压力的计算模型。在上述基于等效体积法的含缺陷海底管道完整性失效判据结构的基础上，同时增加了含小体积缺陷海管的失效压力值，应用最小二乘法分别对37组短缺陷及36组长缺陷共计73组含不同尺寸缺陷管道有限元结果进行拟合；为使得所得到的的计算模型更加准确，以缺陷的长度为依据进行分段拟合，ASME B31G中规定，短腐蚀缺陷的长度小于，当腐蚀长度大于时，则认定为长腐蚀缺陷。依据标准的规定，最后得到了适用于X60海底管道的失效压力计算模型如式（4）、（5）所示。模型式（4）的计算结果和真实值相关系数的平方为0.983，式（5）的相关系数的平方为0.999，模型的准确性非常高。

式中：p为X60管道的失效应力，MPa；D为管道的外径工，mm；t为管道的厚积壁厚，mm。

2.2.2 模型验证

为了验证上述失效压力计算模型的适用性，将式（4）的计算结果与8 组含缺陷X60 管道爆破试验的真实失效压力[22]进行对比，对比结果见表2。经过验证可以发现，本模型对大口径X60管道的适用性较好。

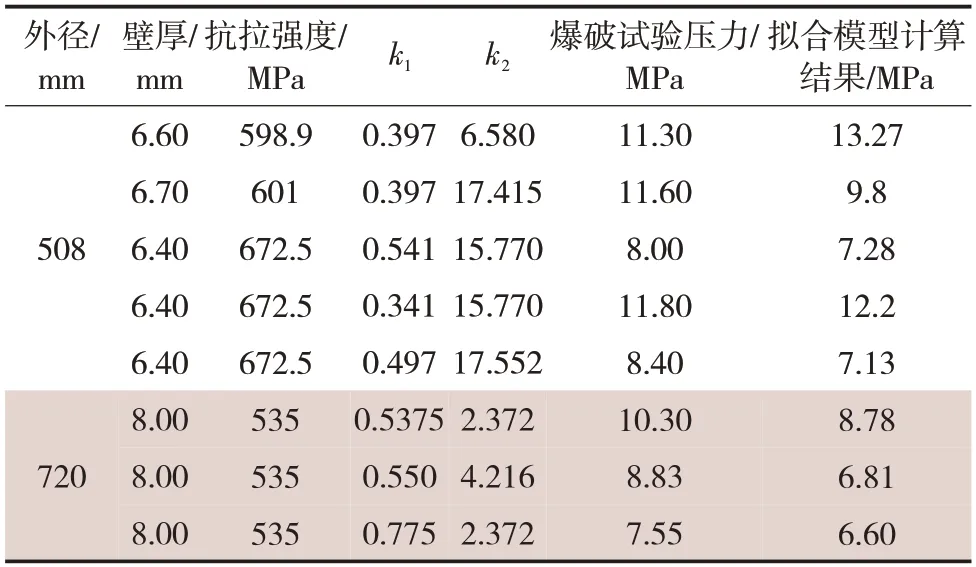
表2 8组缺陷管道的比较结果Tab.2 Comparison results of 8 groups of defective pipelines

通过观察拟合公式的计算结果与真实值的对比图曲线（图6）可以发现，两种结果具有较好的一致性，可以看出本模型对于含缺陷X60管道的适用性较好，进而验证了基于等效体积法的失效判据的合理性。

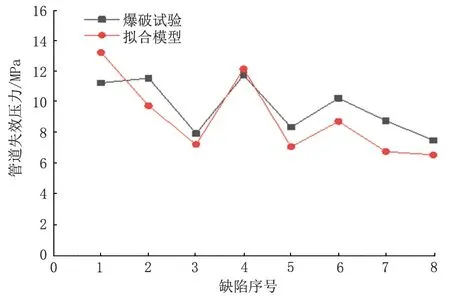
图6 模型计算结果与爆破试验结果对比曲线Fig.6 Comparison curve between model calculation results and blasting test results

3 结论

（1）通过有限元软件对含缺陷管道进行模拟，得到缺陷参数对管道失效模式的影响规律，并基于70 组缺陷管道失效时等效应力超过抗拉强度的相对体积值，归纳出了一种基于等效体积法的含缺陷海底管道完整性失效判据。该判据的出现改善了现有应力失效准则的局限性，进一步完善了塑性失效准则，并弥补了塑性垮塌模型不能进行定量描述的不足，为管道失效评定的研究提供了新思路，在实际应用中，该失效判据也为应用有限元软件进行模拟计算提供了初步的评判依据，具有重要的现实意义，便于应用和推广。

（2）以基于等效体积法的含缺陷海底管道完整性失效判据为基础，应用73 组有限元数据，以缺陷的长度为基准进一步得到了含缺陷X60管道的失效压力计算模型，经验证可以对管道的失效压力进行预测，进而验证了基于等效体积法的含缺陷海底管道完整性失效判据的适用性，并探索出失效判据与失效压力之间的内在联系。

（3）海底管道上缺陷实际的形状和分布是不规律的，需要对含不同形状、不同数量缺陷的海底管道进行进一步研究，从而提高含缺陷海底管道完整性失效判据的适用性，提高含缺陷X60管道失效压力计算模型的准确性。